0 引言
目前, 想要快速、准确地预测无规律、复杂多变的运动目标轨迹, 仍然具有很大的挑战; 然而这样的轨迹预测, 在很多领域都有需要。在自动驾驶领域, 为了避免发生事故, 需要对路上车辆、行人的运动轨迹进行实时预测, 然而车辆的轨迹充满不确定性, 行人的轨迹主观性很强, 比较随意, 使得预测比较困难[1-2]。在围捕运动目标时, 为了更快速、准确地围捕运动目标, 需要对运动目标进行实时预测, 然而围捕方无法准确获知运动目标的运动参数, 而且运动目标具有较强的逃逸能力, 使得围捕方很难完成围捕任务[3-4]。在涂胶应用中, 目标轮廓弯曲复杂。激光传感器在获取目标轮廓时, 目标轮廓容易偏离扫描区域, 因此需要对目标轮廓进行轨迹预测, 使得传感器更加准确地获取轮廓数据。对于无规律、复杂多变的轨迹预测, 设计合适的算法主要面临两个难点: 其一, 轨迹不断变化, 动态更新, 很难实时、快速地预测运动目标的轨迹, 因此对算法的实时性要求较高; 其二, 轨迹无规律, 弯弯曲曲, 复杂多变, 很难准确地预测运动目标的轨迹, 因此对预测算法的准确性要求较高。
常用的动态轨迹预测算法主要有3类[5-6]。第1类是基于曲线拟合的轨迹预测算法, 所选取的曲线通常为多项式曲线。传统的多项式曲线拟合轨迹预测算法(polynomial curve fitting trajectory prediction algorithm, PCFTPA)具有原理简单、计算量小、预测速度快等特点, 在对实时性要求较高的场合, 具有很好的优势。胡俊等[7]在研究围捕机器人对移动目标的快速围捕时, 考虑到移动目标运动轨迹复杂多变, 机器人需要先通过预测算法快速地预判移动目标未来一小部分的运动轨迹, 然后才能根据预测的轨迹对运动目标实施围捕这一情况, 选择曲线拟合轨迹预测算法, 该算法很好地满足了快速预测的需求。张强等[8]在嵌入式态势显示设备中, 针对运动目标轨迹更新延迟的问题, 提出基于曲线拟合的轨迹预测算法。该算法只需将靠近预测点的部分采样点进行拟合, 无需存储大量的历史数据, 使得算法计算量小、所需存储空间较小, 很好地解决了嵌入式态势显示设备对运动目标轨迹更新延迟的问题。李世杰等[9]需要对高超声速再入滑翔目标进行轨迹预测。考虑到运动目标具有较强的机动能力, 其轨迹是复杂多变的, 并且预测方无法准确获知运动目标实际机动模式的信息, 作者采用最小二乘曲线拟合算法进行预测。Cao等[10]充分利用多项式曲线拟合的快速性优势, 实时预测动态目标在未来一小段时间内的运动轨迹, 进而实现对动态目标的围捕。可见, PCFTPA应用于轨迹预测的优势非常明显, 即计算量小、预测速度快。然而传统的多项式曲线拟合主要是通过输入样本点求出多项式的系数, 这样一条理论曲线对于真实、复杂多变的轨迹并不能很好地逼近, 导致多项式曲线拟合对于复杂多变的轨迹预测无法取得较好的预测效果。因此, 很多学者尝试研究第2类、第3类轨迹预测算法。第2类是基于自适应滤波器的轨迹预测算法, 其优点是对采样点的异常情况适应性强[11-14]。为了更准确地预测飞机爬升的轨迹, Thipphavong等[15]提出了一种基于观测数据动态调整模型参数的自适应轨迹预测算法。Han等[16]为了解决具有动态时间尺度的浮萍飘移轨迹预测问题, 设计了一种自适应参数变时间尺度卡尔曼滤波器, 可精确地预估浮萍的轨迹。第3类是基于神经网络的动态轨迹预测算法[17-21], 该算法对于非线性系统具有很好的映射能力。Zhang等[22]为了准确地预测乒乓球在未来时刻的位置, 提出基于多层神经网络的轨迹预测算法。Akabane等[23]为了使移动机器人更准确地跟随人, 提出了基于长短期记忆(long short-term memory, LSTM)网络的轨迹预测算法。Yang等[24]为了更合理地预测行人的轨迹, 提出了一种基于图注意和卷积LSTM的模型; 该模型具有较高的预测精度, 生成的轨迹更符合社会理性和物理约束。虽然第2类、第3类算法对于复杂多变的轨迹预测准确率较高, 但实时性较差, 因此本文选择第1类算法进行研究。第1类轨迹预测算法研究的不足为: ①没有对预测误差较大的轨迹部位进行准确识别并加以处理; ②未考虑采样点间隔不一对轨迹预测的负面影响; 原始点数据采集时, 由于采集速度不均, 导致点与点之间的间隔大小不一以及轨迹变化的连续性受影响, 对轨迹预测的结果有负面影响; ③忽略了采样点之间时序上及空间上的关系。数据采集是有先后顺序的, 而且相邻两个采样点变化并不会很大, 因此相邻两次预测的误差较接近。
因此, 本文在PCFTPA基础上, 提出一种改进的PCFTPA (improved PCFTPA, IPCFTPA)。改进之处为: ①通常预测误差较大的部位, 轨迹的曲率、挠率值也较大。本文通过曲率、挠率阈值确定算法(curvature and torsion thresholds determination algorithm, CTTDA)获得曲率、挠率阈值, 建立曲率、挠率及误差的对应关系, 从而将可能导致预测误差较大的轨迹部位识别出来并加以处理; ②多项式曲线拟合轨迹预测受轨迹不规则程度的影响, 另外采样点之间间隔不一, 因此本文提出插值滚动预测算法(interpolation-rolling prediction algorithm, IRPA)。通过样条曲线插值, 得到采样间隔较小且较均匀的点, 然后截取末了一小段轨迹进行预测, 使得所需预测的轨迹更加规则, 采样点也更加均匀。在这些点的基础上, 得到少于预测目标点数、较准确的预测点, 接着将这些预测点当做待拟合点再次进行预测, 如此循环, 直到完成预测任务; ③通过双误差预测值更新算法(double errors predictive value update algorithm, DEPVUA)建立采样点之间时序上及空间上的关系。该算法不仅将未更新时的预测值误差进行了考虑, 还将单误差预测值更新时的误差也进行了考虑, 进而建立双误差预测值更新机制, 实现对预测值的纠正。
1 多项式曲线拟合轨迹预测模型
1.1 问题描述及轨迹表示
图 1(a)中, L为运动目标的实际轨迹, L′为L的未来一小段的预测轨迹。由于目标不断运动, 轨迹L的形状也不断变化, 因此需要根据历史轨迹实时、动态地预测L′。
图1
轨迹L可表示为
假设这些离散的点均在空间参数曲线上
其中, t是曲线的参数。那么, 曲线r(t)的空间特征可以反映轨迹的空间特征。因此, 可以通过对曲线r(t)的研究, 研究轨迹L的预测。
本文选择确定的空间参数曲线r(t)表示空间中运动目标的轨迹, 并对r(t)作如下限定:
(1) 曲线为连续光滑的曲线, 即r(t)具有连续的一阶导数, 排除曲线包含比较“尖锐”的点;
(2) 曲线为正则曲线, 即在曲线的每一点处, r′(t)≠0, 排除了切向量变化不连续的特殊点, 比如带尖点的曲线;
(3) 对r(t)的采样频率远大于r(t)最大频率的2倍。
1.2 多项式曲线拟合算法原理
对于空间中的轨迹, 可在投影面中分别进行曲线拟合。设投影面上的采样点为{(xi, yi), i=1, 2, …, N}, 用k(k < N)次多项式进行拟合。该多项式可表示为
根据采样点, 通过最小二乘法, 便可计算出多项式的系数。
1.3 基于多项式曲线拟合的空间轨迹预测模型
图2
步骤1 选取N个历史轨迹点, 作为待拟合点(滑动窗口S内);
步骤2 根据待拟合点进行最小二乘拟合, 得到一条与轨迹相近的空间曲线;
步骤3 通过一定的方式外推得到未来的一小段轨迹L′上的轨迹点;
步骤4 当获取新的采样点时, 滑动窗口S往前一步, 回到步骤2继续进行预测。
图 3更直观地展示了轨迹预测模型的动态性。
图3
1.4 评价指标
式中: P′i为预测点; Pi为实际点; M为预测点数。
FDE为最后一个预测点的距离误差, 主要体现最后一个预测点的偏离程度。其表达式为
式中: P′M为第M个预测点; PM为与P′M对应的实际点。
2 改进的曲线拟合轨迹预测算法
2.1 曲率与挠率阈值的确定
对于空间参数曲线r(t), 其在t处的曲率为
r(t)在t处的挠率为
在轨迹预测时, 预测误差与曲率、挠率值一般具有如下的关系: 当预测误差较大时, 曲率或挠率值也较大, 即曲线弯曲程度较严重的部分或扭曲程度较严重的部分预测准确率较低; 反之亦然。因此, 可通过确定曲率、挠率阈值, 识别轨迹预测误差较大的部分。CTTDA算法的流程如下。
算法1 CTTDA 输入 动态更新的待拟合点集P
输出 阈值Kmax
1. set errorMax; //用于确定局部误差最大值
2. for each prediction
3. //K为待拟合点的曲率或挠率
4. K=calculate K(P);
5. K_mean=mean(K); //计算K的平均值
6. P′=curvefitPredict(P); //PCFTPA
7. errorMean=getMeanError(P, P′);
8. //找到误差局部最大值
9. if errorMean>errorMax and other conditions
10. errorMax=errorMean;
11. end if
12. //确定曲率或挠率阈值
13. if errorMean>errorMax and other conditions
14. Kmax=K_mean;
15. end if
16. end for
17. output Kmax
(1) 设置errorMax初始值(第1行);
(2) 实时计算待拟合点集的曲率或挠率平均值(第4行、第5行);
(3) 根据待拟合点预测未来的轨迹点, 并计算误差(第6行、第7行);
(4) 确定局部误差最大值(第9~11行);
(5) 当误差值超过errorMax, 将当前的曲率或挠率平均值作为曲率、挠率的阈值Kmax(第15~17行);
(6) 对errorMax可以先赋较小值, 并保证先确定误差局部最大值errorMax, 然后才执行Kmax的赋值。另外, 局部误差最大值和曲率、挠率阈值均只确定一次。
2.2 IRPA
2.2.1 轨迹预测与采样间隔的关系
缩小采样间隔可以提高轨迹预测准确率。如图 4所示, 当输入的待拟合点缩小采样间隔时, 轨迹采样点数增多, 滑动窗口内的轨迹变短, 所代表的轨迹段更有规律, 此时相同阶数的拟合函数更容易逼近该曲线段, 预测结果也会更准确。
图4
图4
缩小采样间隔的轨迹预测示意图
Fig.4
Trajectory prediction schematic diagram with the reduced sampling interval
2.2.2 算法具体步骤
IRPA算法充分利用了采样间隔对轨迹预测的影响, 通过对采样点进行插值, 得到更密集的点, 然后选择靠近预测位置的部分点进行预测。由于所预测的点准确率很高, 因此可将其近似当做真实的点, 选取这些点继续进行预测, 就可以滚动地预测所需的轨迹。
| 算法2 IRPA |
| 输入 待拟合点集P 输出 预测点P′(最终预测M个点) |
| 1. set predictNumber=K; //单次预测点数 2. newP=interp1(P); //插值得到较密的点集 3. N=M/K; //M为K的倍数, N为滚动次数 4. for i=1 to N 5. //取最后N个点作为待拟合点 6. P_=newP(end-N: end); 7. tempP=curvefitPredict(P_); //PCFTPA 8. //将预测点放进待拟合点, 进行滚动预测 9. newP=append(tempP); 10. //保存每一轮的预测结果 11. P′=append(tempP); 12. end for 13. output P′ |
具体步骤如下:
(1) 确定单次预测点数K(第1行);
(2) 通过插值, 缩小采样间隔(第2行);
(3) 对插值后的点集 newP, 取最后N个点作为待拟合点P_(第6行);
(4) 对待拟合点进行拟合, 得到K个预测点 tempP(第7行);
(5) 将所预测的点 tempP添加到 newP点集中, 构成新的待拟合点集(第9行);
(6) 循环预测N次, 输出预测点P′(第13行)。
2.3 DEPVUA
图5
基于相邻两次预测误差的规律, 可得到如下的预测值更新策略。设
则
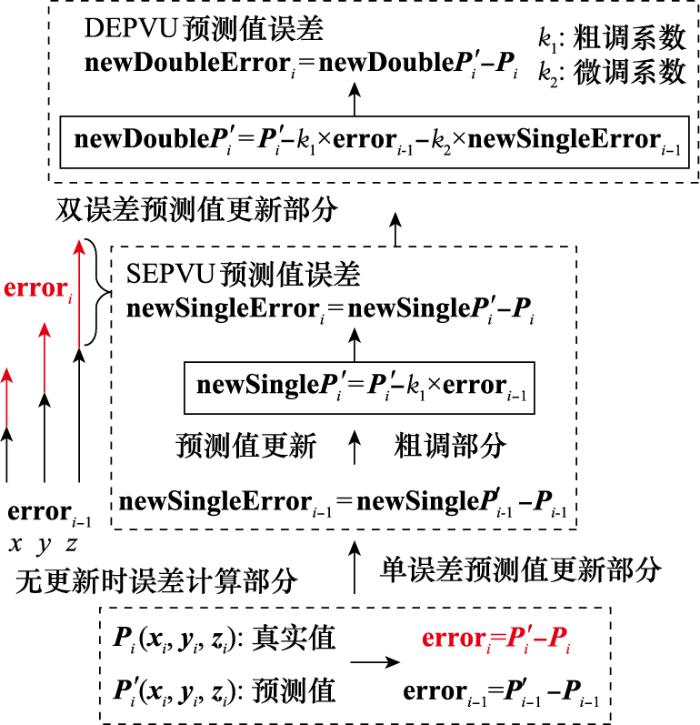
式中: P′i-1为第i-1次预测值, Pi-1为第i-1次真实值, newSingleP′i为第i次预测时通过单误差预测值更新算法(single error predictive value update algorithm, SEPVUA)所计算的预测值, newSingleError′i为其对应的误差; newDoubleP′i为双误差更新得到的预测值, 该值即为算法最终的预测值。k1为预测值更新粗调系数, k2为预测值更新微调系数, k1、k2均大于0。单步预测时, 双误差预测值更新示意图如图 6所示。
图6
图6
单步预测中双误差预测值更新示意图
Fig.6
Double error prediction value update schematic diagram in single-step prediction
由图 6可知, “双误差”指的是无更新时计算的预测值误差 errori-1, 以及 SEPVUA所计算的误差 newSingleError′i-1。
对于k(k>1)步预测, 由于第i次预测时, 第i-1次预测中的k个误差值只有第一个误差可利用, 因此 errori-1只能取近似组合值。如图 7所示, 为 errori-1的取值过程(假设k取3)。
图7
图7
多步预测第i-1次误差取值过程(k=3)
Fig.7
Process of error value extraction in step i-1 in multi-step prediction (k=3)
具体算法流程如下:
| 算法3 DEPVUA |
| 输入 预测点P′i, 上一次预测误差errori-1 输出 更新的预测点newDoubleP′i |
| 1. for i=1, 2, … 2. //单误差预测值更新 3. if i>k 4. newP′i=P′i - k1×errori-1; 5. newSingleErrori=newSingleP′i-Pi; 6. end if 7. if i>k+1 8. //双误差预测值更新 9. newDoubleP′i= 10. P′i-k1×errori-1-k2×newSingleErrori-1; 11. end if 12. end for 13. output newDoubleP′i |
2.4 预测值偏差限制
相邻两次预测滑动窗口内的数据变化并不是很大, 预测值之间也不会差别太大,因此可以限制预测值之间的偏差在一定的范围。设
式中: P′i为第i个预测点, 则error′i限制如下:
式中: k1、k2为偏差的缩放系数, 满足0 < k2 < 1 < k1。
2.5 算法流程
本文所设计IPCFTPA算法的流程如图 8所示。
图8
(1) 数据预处理阶段, 对于不光滑的轨迹数据需进行平滑处理, 比如采用3次B样条曲线拟合;
(2) 曲率、挠率阈值可设置较大的初始值, 使得算法一开始先按PCFTPA进行预测;
(3) 一旦曲率、挠率阈值最终确定, CTTDA不再执行;
(4) 当当前曲率、挠率值小于阈值时, 说明该位置误差在可接受的范围, 选择PCFTPA进行预测; 当曲率、挠率值大于阈值时, 说明该位置误差可能较大, 选择IRPA进行预测;
(5) 对于PCFTPA及IRPA的预测值, 均需通过DEPVUA进行更新, 并将更新过的预测值作为最终的预测值。
3 算法验证
为充分验证本文算法的可行性和有效性, 选择3组仿真数据及3组真实数据进行详细的对比分析。本文将所提算法与PCFTPA、基于卡尔曼滤波的轨迹预测算法(Kalman filtering trajectory prediction algorithm, KF)、基于反向卷积神经网络的轨迹预测算法(back propagation neural network trajectory prediction algorithm, BPNN)、LSTM作对比。另外, 本文研究的算法针对空间中复杂多变、未知的轨迹, 因此LSTM和BPNN没有提前训练模型, 而是根据部分历史轨迹点实时训练并预测。本次实验所使用的仿真软件为Matlab R2019b。
3.1 数据描述
表1 3类仿真数据及其描述
Table 1
| 数据 | 参数方程 | 描述 |
| 1 | t∈[0, 2π] | |
| 2 | / | 3次B样条曲线, 点数230 |
| 3 | t∈[0, 8π] 点数为300 |
图9
(2) 3组真实数据分别从3组不同的三维轮廓数据源提取, 数据特征类似, 处理方式也类似。本文对真实数据1作详细说明。真实数据1如图 10所示。该数据是通过三维激光传感器扫描得到目标轮廓的点云, 然后提取目标轮廓的中心线而得。轨迹数据点为370个。
图10
图11
3.2 重要参数选取
以仿真数据1为例, 探究IPCFTPA中重要参数(多项式拟合系数、插值间隙、粗调系数和微调系数)对轨迹预测的影响。
图12
图13
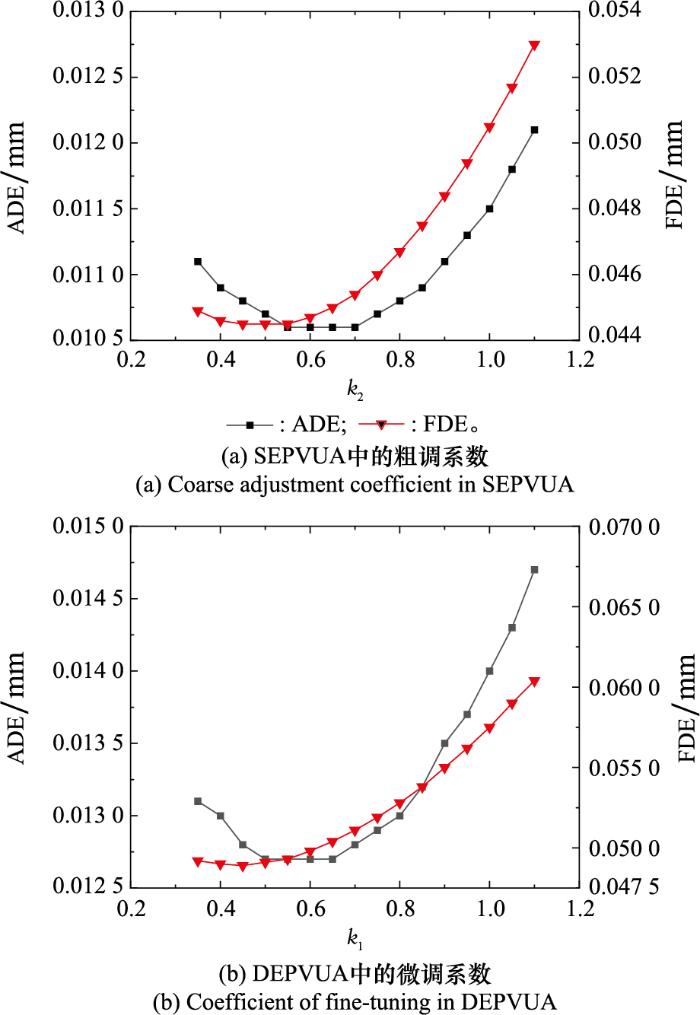
图13
调节系数对轨迹预测的影响
Fig.13
Influence of adjustment coefficient on trajectory prediction
由图 13可知, k1取0.5、k2取0.55时对轨迹预测效果最好。
3.3 对比实验
图 14用仿真数据1对比了PCFTPA、IRPA、SEPVUA及DEPVUA的ADE情况。其中, 相对于PCFTPA, IRPA的ADE降低了40.3%, SEPVUA的ADE降低了51.71%, DEPVUA的ADE降低了59.7%, 验证了DEPVUA的可行性和有效性。后续IPCFTPA均采用IRPA+DEPVUA。
图14
图14
仿真数据1不同算法不同位置的ADE情况
Fig.14
ADE situation of different algorithms at different positions in simulation data 1
图 15用仿真数据1探究不同方法、不同预测步长对轨迹预测的影响。
图15
图15
仿真数据1用不同方法在不同预测步长下的轨迹预测情况
Fig.15
Trajectory prediction with different prediction steps by different methods in simulation data 1
表2 仿真数据2不同方法的预测情况
Table 2
| 算法 | ADE/mm | FDE/mm | 耗时/ms |
| IPCFTPA | 0.004 4 | 0.015 9 | 3.902 3 |
| PCFTPA | 0.008 2 | 0.027 0 | 0.737 3 |
| KF | 2.910 6 | 3.403 9 | 0.602 4 |
| BPNN | 0.057 5 | 0.181 2 | 1 130.530 0 |
| LSTM | 1.971 4 | 4.581 6 | 8 519.360 0 |
表3 仿真数据3不同预测方法的预测情况
Table 3
| 算法 | ADE/mm | FDE/mm | 耗时/ms |
| IPCFTPA | 0.323 3 | 1.150 6 | 1.837 3 |
| PCFTPA | 0.558 3 | 1.827 8 | 0.754 8 |
| KF | 9.896 5 | 11.63 | 0.786 9 |
| BPNN | 1.107 4 | 3.312 | 1 460.910 0 |
| LSTM | 6.096 7 | 12.988 | 3 656.130 0 |
表4 真实数据1不同方法预测情况
Table 4
| 算法 | ADE/mm | FDE/mm | 耗时/ms |
| IPCFTPA | 0.864 7 | 2.167 3 | 3.833 2 |
| PCFTPA | 1.539 5 | 4.294 9 | 0.750 8 |
| KF | 3.384 1 | 3.899 3 | 0.889 5 |
| BPNN | 1.228 1 | 2.722 1 | 1 450.820 0 |
| LSTM | 4.968 1 | 10.324 | 6 919.180 0 |
表 5统计了不同数据IPCFTPA相较于PCFTPA的ADE、FDE降低比例情况。其中, KADE为ADE降低比例, KFDE为FDE降低比例。
表5 不同数据IPCFTPA相较于PCFTPA的ADE、FDE降低比例
Table 5
| 数据 | KADE | KFDE |
| 仿真数据1 | 59.70 | 48.07 |
| 仿真数据2 | 46.34 | 32.65 |
| 仿真数据3 | 42.09 | 37.05 |
| 仿真数据均值 | 49.38 | 39.26 |
| 真实数据1 | 43.83 | 49.54 |
| 真实数据2 | 32.99 | 26.78 |
| 真实数据3 | 31.64 | 25.64 |
| 真实数据均值 | 36.15 | 33.99 |
| 总均值 | 42.77 | 36.62 |
4 结束语
本文提出基于PCFTPA的算法IPCFTPA。改进之处主要有3点: ①通过CTTDA确定曲率、挠率阈值, 并根据该阈值识别预测误差较大的轨迹部位; ②通过IRPA对预测误差较大的部位进行插值滚动预测; ③通过DEPVUA对预测值进行更新, 建立相邻两次预测中时间及空间上的关系, 提高预测准确率。实验结果表明, IPCFTPA相较于PCFTPA, ADE平均下降了42.77%, FDE平均下降了36.62%, 单次平均预测时间略有增加; 与LSTM、BPNN轨迹预测算法相比, IPCFTPA在单次预测耗时上具有非常大的优势; 与KF、LSTM、BPNN相比, IPCFTPA预测准确率具有明显的优势。另外, 在多项式曲线拟合用于轨迹预测的算法中, 多项式系数也呈现出一定的规律。下一步将研究多项式系数的变化规律, 进一步提高轨迹预测的准确性, 以充分发挥多项式曲线拟合在轨迹预测中的优势。
参考文献
PoPPL: pedestrian trajectory prediction by LSTM with automatic route class clustering
[J].DOI:10.1109/TNNLS.2020.2975837 [本文引用: 1]
Road-aware trajectory prediction for autonomous driving on highways
[J].DOI:10.3390/s20174703 [本文引用: 1]
移动目标轨迹预测方法研究综述
[J].
A review of prediction methods for moving target trajectories
[J].
A review of tracking and trajectory prediction methods for autonomous driving
[J].DOI:10.3390/math9060660 [本文引用: 1]
基于动态预测目标轨迹和围捕点的多机器人围捕算法
[J].
A multi-robot hunting algorithm based on dynamic prediction for trajectory of the moving target and hunting points
[J].
基于曲线拟合的机动目标轨迹预测算法研究
[J].
Research of maneuvering target tra-jectory prediction based on curve fitting
[J].
基于控制变量估计的高超声速再入滑翔目标轨迹预测算法
[J].
Trajectory prediction algorithm for hypersonic reentry gliding target based on control variables estimation
[J].
Hunting algorithm for multi-AUV based on dynamic prediction of target trajectory in 3D underwater environment
[J].DOI:10.1109/ACCESS.2020.3013032 [本文引用: 1]
3D multi-object tracking with adaptive cubature Kalman filter for autonomous driving
[J].
Real-time object tracking based on an adaptive transition model and extended Kalman filter to handle full occlusion
[J].DOI:10.1007/s00371-019-01652-3
An adaptive approach to vehicle trajectory prediction using multimodel Kalman filter
[J].DOI:10.1002/ett.3734 [本文引用: 1]
Adaptive algorithm to improve trajectory prediction accuracy of climbing aircraft
[J].
Estimation of buoy drifting based on adaptive parameter-varying time scale Kalman filter
[J].DOI:10.1080/23307706.2020.1808863 [本文引用: 1]
A 4D trajectory prediction model based on the BP neural network
[J].DOI:10.1515/jisys-2019-0077 [本文引用: 1]
Pedestrian trajectory prediction in heterogeneous traffic using pose keypoints-based convolutional encoder-decoder network
[J].DOI:10.1109/TCSVT.2020.3013254
A tracking and predicting scheme for ping pong robot
[J].
Pedestrian trajectory prediction based on transfer learning for human-following mobile robots
[J].DOI:10.1109/ACCESS.2021.3111917 [本文引用: 1]
PTPGC: pedestrian trajectory prediction by graph attention network with Conv- LSTM
[J].DOI:10.1016/j.robot.2021.103931 [本文引用: 2]
A symbolic analysis of relay and switching circuits
[J].DOI:10.1109/EE.1938.6431064 [本文引用: 1]
Cutting force prediction considering tool path curvature and torsion based on screw theory
[J].
Curvature based sampling of curves and surfaces
[J].DOI:10.1016/j.cagd.2017.11.004
High-quality point sampling for B-spline fitting of parametric curves with feature recognition
[J].DOI:10.1016/j.cam.2018.04.008 [本文引用: 1]
Research on model predictive trajectory following control of automatic vehicle considering prediction error
[J].DOI:10.1504/IJWMC.2021.119062 [本文引用: 1]
Smooth curve fitting of mobile robot trajectories using differential evolution
[J].DOI:10.1109/ACCESS.2020.2991003 [本文引用: 1]