在低空物流无人机运行方面, 文献[5 ]考虑了无人机在人道主义物流最后一英里配送中的应用, 提出一种通过无人机将轻型救援物品(如疫苗、纯净水等)运送到受灾地区的优化模型。文献[6 ]提出利用无人机完成医疗保健运输更加及时、高效和经济, 设计了无人机医疗网络运输的决策模型。文献[7 ]关注了无人机在物流配送中区别于普通地面物流的基本特征, 考虑无人机飞行时间、装载能力、货物重量对飞行能力的影响, 提出一种混合整数线性规划公式和任务分配启发式算法, 并通过数值示例进行测试。文献[8 ]研究了无人机在人口稠密的城市环境中的运行风险, 利用空间模拟系统进行风险评估。文献[9 ]指出越来越多的物流公司都在研究使用无人机进行快递交付, 针对无人机投送的容量限制问题, 提出一种混合元启发式方法, 仿真结果证实了所提算法的有效性。文献[10 ]考虑权重系数、时间窗约束、无人机约束等建立了无人机物流任务分配模型, 采用改进粒子群优化算法求解, 仿真结果表明该算法能够有效解决无人机物流任务分配问题。文献[11 ]提出基于改进人工势场-快速扩展随机树算法, 以实现无人机在物流配送中准确、快速的路径规划。文献[12 ]使用牛顿运动定律和伽利略自由落体评估无人机碰撞概率密度, 通过路径规划保证无人机避开人口密集区域。
在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议。文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突。文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法。文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流。文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量。文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间。文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题。文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突。文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙。文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题。
借鉴航班时刻分配的有关研究, 文献[23 ]分析了双目标资源约束调度来解决战略机场时刻分配问题, 提出一种新型混合启发式算法, 并以希腊机场的实际时隙数据验证了所提算法的准确性。文献[24 ]介绍了一种协助人工进行初始时隙分配的优化决策支持工具, 该工具在可接受的时间内生成有效的时隙解决航班分配问题。文献[25 ]研究了阻塞缓解策略, 提出一种航班时隙分配模型和解决方案, 通过调度时刻来缓解机场拥堵。文献[26 ]提出一种考虑时刻调度效率和公平性的双目标机场时刻调度模型, 研究了考虑历史时隙使用权和不考虑历史时隙使用权的机制下时隙调度效率-公平的权衡, 以实现航班时隙调度。文献[27 ]在文献[26 ]的基础上提出了考虑效率、公平性和航空公司偏好的多目标两阶段时刻分配机制。文献[28 ]提出一种整数线性规划模型, 通过周转时间限制飞机轮转, 用于在欧洲范围内优化机场时刻分配。文献[29 ]提出一种符合全球航班时刻指南的优化模型, 将机场时刻分配给航空公司。
目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少。无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率。因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配。
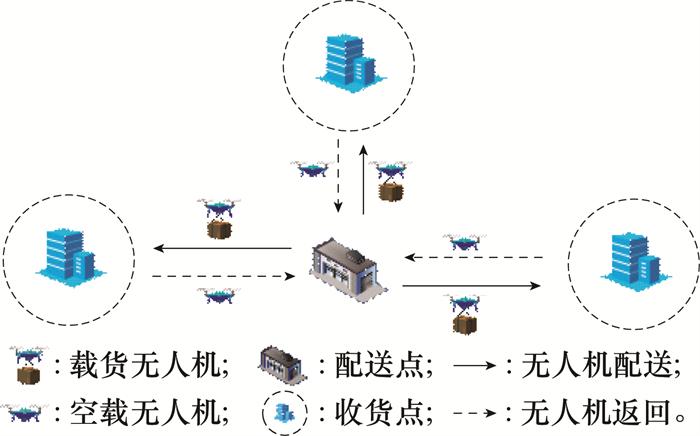
某城市片区的物流配送点, 利用无人机装载小批量货物运输至收货点, 货物运输过程拟采用可垂直起降的充电旋翼无人机, 无人机任务执行完毕后返回配送中心。现有配送点对即将执行的飞行任务向管制部门提交飞行申请, 为保证城市空域范围内无人机避免冲突有序飞行, 管制部门需要在空域使用前进行飞行计划审批与飞行时刻调配, 尽可能确保飞行安全。本模型的主要假设如下: ①物流配送点和各个收货点的位置已知; ②每架无人机需要从配送点的不同起降点出发, 沿既定航路飞往收货点, 完成其配送任务后返回配送点; ③每个起降点有多架无人机等待起飞, 每架无人机单次只服务一对起降点; ④无人机满电状态出发, 飞行速度预先设定, 出发后不再接受新的任务安排。城市低空物流无人机配送模式如图 1 所示。
图1
城市低空物流无人机配送模式
Fig.1
Logistics unmanned aerial vehicle distribution mode in urban low-altitude airspace
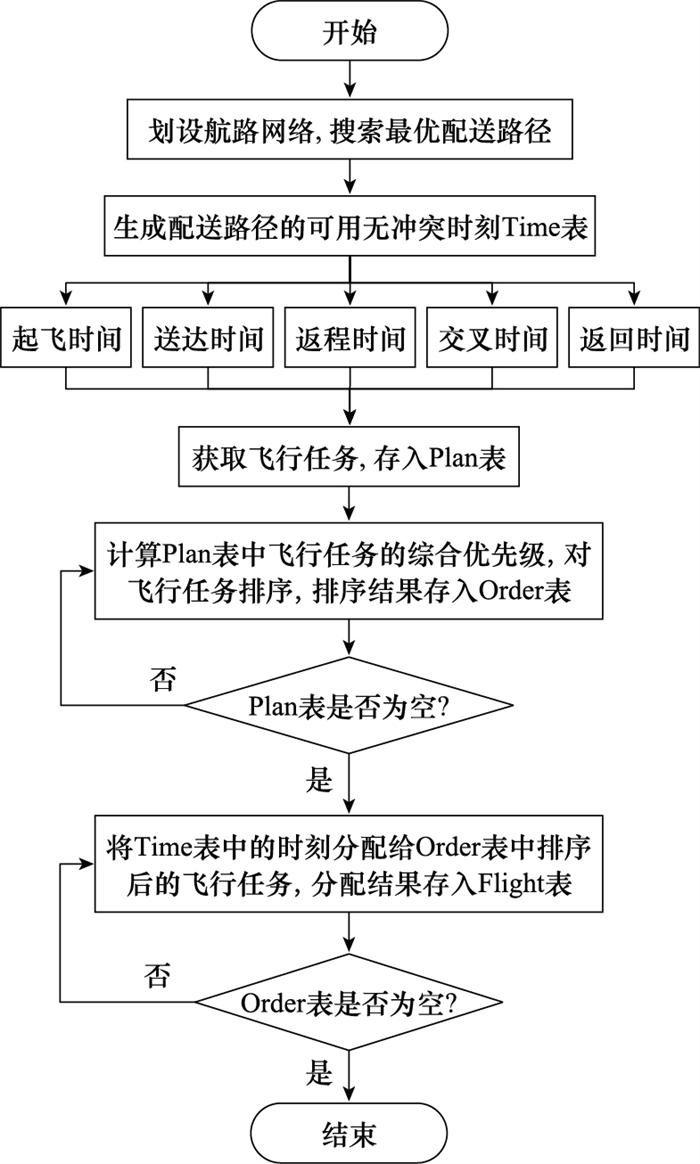
图2
基于综合优先级的飞行计划预先调配算法流程
Fig.2
Algorithm flow of flight plan pre-allocation based on comprehensive priority
步骤6 飞行任务分配时刻。建立Flight表, 依次从Time表取出时刻, 依次从Order表取出飞行计划, 将时刻分配给飞行计划, j =j +1, 此时, 每条计划都获取到一组起飞时间T dep ij T arr ij T return ij x ij x ij
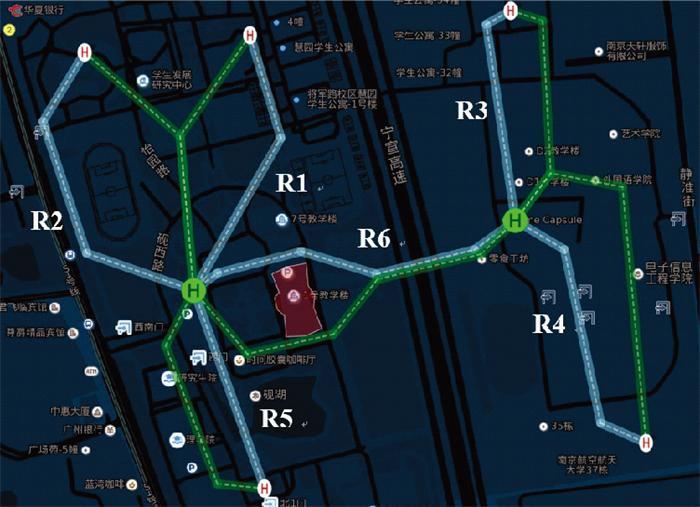
根据配送点和收货点在航路网络中的位置, 搜索从配送点至收货点避让障碍物的低空飞行路径即为无人机配送路线。因两校区之间存在高速公路, 经天桥相连, 无人机只可在天桥上方低空空域往返两区, 且去程与回程分别在保持纵向间隔的不同高度层, 不存在航路冲突。如图 3 所示, 其中绿色圆点表示配送点, 白色圆点表示收货点, 配送点和收货点的蓝色航路表示无人机去程, 绿色航路表示无人机回程。
图3
某校园配送航路示意图
Fig.3
Schematic diagram of a campus distribution routes
4条航路的无人机从同一个公共配送点出发, 飞至收货点等待顾客取货完成后起飞返程, 最终回到公共配送点。由上述时刻表可知, 所有航路无人机在公共配送点的起飞时间为[08:00:00, 08:00:10, 08:00:20, …], 满足间隔10 s的安全约束; 返回配送点的到达时间为[08:02:15, 08:02:25, 08:02:35, …], 满足间隔10 s的安全约束。航路R1和R2的无人机经过交叉点处的时间为[08:01:45, 08:02:05, 08:02:25, …], 满足间隔10 s的安全约束。每条航路无人机的起飞间隔为40 s, 返程间隔为40 s, 返回配送点间隔为40 s, 均满足10 s的安全约束。因此, 无人机在航路网络中运行时, 飞行路径上的冲突可以通过飞行时刻的调配进行解脱, 使得无人机可以在起降点和航路交叉口顺序通行。
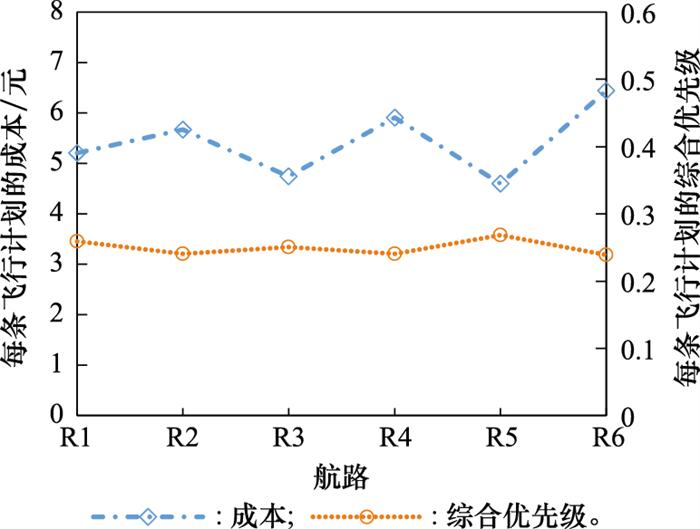
基于6条航路信息得到08:00-10:00时刻表最大可安排数量C a C a 图 4 所示。
图4
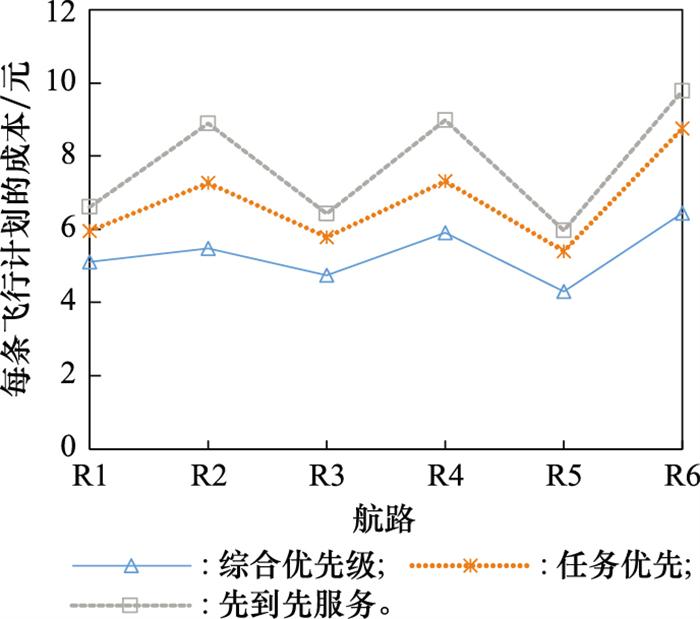
每条飞行计划的成本和综合优先级变动
Fig.4
Cost and comprehensive priority changes for each flight plan
由图 4 可知, 每条飞行计划的成本与综合优先级变化趋势相反, 因为优先级高的计划会先进行排序, 分配到较早的时刻, 出现延误的可能性小, 因此成本低。对于每条航路, 待分配计划的数量越多, 每条飞行计划的成本越高, 由于航路R5距离最短, 每条计划的成本最低, 航路R6距离最长, 每条计划的成本最高。
图5
不同算法求解对比
Fig.5
Comparison of different algorithm solutions
图6
不同权重对每条飞行计划的成本影响
Fig.6
Impact of different weights on cost of each flight plan
由图 6 可知, 点的大小表示飞行计划成本的高低, 随着权重ω 1 、ω 2 和ω 3 取值变动, 不同航路之间成本变动趋势相似, 取图 6 中成本最小的点, 如橙色标注所示, 绘制其至3个坐标轴的垂线, 可知使成本最低的综合优先级最优权重组合为ω 1 =0.2, ω 2 =0.4, ω 3 =0.4, 航路网络中每条飞行计划的成本为5.42元。
[1]
CONSULTING P. The future of vertical mobility: sizing the market for passenger, inspection, and goods services until 2035[EB/OL]. [2022-04-15]. https://www.porsche consulting.com/fileadmin/docs/04_Medien/Pub likationen/TT1371_The_Future_ of_Vertical_Mobility/The_Future_of_Vertical_Mobility_A_Porsche_Consulting_study__C_2018.pdf .
[本文引用: 1]
[2]
STANLEY M. Urban air mobility flying cars: Investment implications of autonomous urban air mobility[EB/OL]. [2022-04-15]. https://www.morganstanley.com/ideas/autonomous-aircraft .
[本文引用: 1]
[3]
GOYAL R. Urban air mobility(UAM) market study[EB/OL]. [2022-04-15]. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20190001472.pdf .
[本文引用: 1]
[4]
SWADESIR L, BIL C. Urban air transportation for Melbourne metropolitan area[C]//Proc. of the AIAA Aviation 2019 Forum, 2019.
[本文引用: 1]
[5]
RABTA B WANKMVLLER C REINER G A drone fleet model for last-mile distribution in disaster relief operations
[J].International Journal of Disaster Risk Reduction ,2018 ,28 ,107 -112 .
DOI:10.1016/j.ijdrr.2018.02.020
[本文引用: 2]
[6]
SCOTT J, SCOTT C. Drone delivery models for healthcare[C]// Proc. of the Hawaii International Conference on System Sciences, 2017.
[本文引用: 1]
[7]
SONG B D PARK K KIM J Persistent UAV delivery logistics: MILP formulation and efficient heuristic
[J].Computers & Industrial Engineering ,2018 ,120 ,418 -428 .
[本文引用: 1]
[8]
CHEN A Z J, MO J P T. Modelling of unmanned aerial vehicle deliveries in populated urban areas for risk management[C]//Proc. of the International Conference on Software, Knowledge, Information Management & Applications, 2017: 61-66.
[本文引用: 1]
[9]
DUAN F L, LI X H, ZHAO Y. Express UAV swarm path planning with VND enhanced memetic algorithm[C]//Proc. of the International Conference on Computing and Data Engineering, 2018: 93-97.
[本文引用: 1]
[10]
JIANG X W, ZHOU Q, YE Y. Method of task assignment for UAV based on particle swarm optimization in logistics[C]//Proc. of the International Conference on Intelligent Systems, 2017: 113-117.
[本文引用: 1]
[11]
ZHAO Y Q LIU K LU G H et al .Path planning of UAV delivery based on improved APF-RRT* algorithm
[J].Journal of Physics Conference Series ,2020 ,1624 ,042004 .
DOI:10.1088/1742-6596/1624/4/042004
[本文引用: 1]
[12]
LIN C E SHAO P C Failure analysis for an unmanned aerial vehicle using safe path planning
[J].Journal of Aerospace Information Systems ,2020 ,17 (7 ):358 -369 .
DOI:10.2514/1.I010795
[本文引用: 2]
[13]
傅辰涛, 王宏伟. 飞行冲突探测与调配辅助决策过程研究[C]// 第一届空中交通管理系统技术学术年会论文集, 2018: 74-77.
[本文引用: 2]
FU C T, WANG H W. Research on flight conflict detection and deployment assistant decision-making process[C]//Proc. of the Annual Conference on Air Traffic Management System Technology, 2018: 74-77.
[本文引用: 2]
[14]
TAN Q Y, WANG Z K, ONG Y S, et al. Evolutionary optimization-based mission planning for UAS traffic management(UTM)[C]//Proc. of the International Conference on Unmanned Aircraft Systems, 2019: 952-958.
[本文引用: 2]
[15]
田宇 ,张洪海 ,钱晓鹏 ,等 .低空通航飞行计划预先调配方法研究
[J].武汉理工大学学报(交通科学与工程版) ,2020 ,44 (3 ):444 -449 .
URL
[本文引用: 2]
TIAN Y ZHANG H H QIAN X P et al .Research on pre-allocation method of low-altitude general aviation flight plan
[J].Journal of Wuhan University of Technology (Transportation Science and Engineering Edition) ,2020 ,44 (3 ):444 -449 .
URL
[本文引用: 2]
[16]
高虎 ,褚映红 ,杨明 ,等 .通用航空飞行计划处理系统的设计与实现
[J].现代导航 ,2019 ,10 (3 ):187 -190 .
DOI:10.3969/j.issn.1674-7976.2019.03.007
[本文引用: 2]
GAO H CHU Y H YANG M et al .Design and realization of general aviation flight plan system
[J].Modern Navigation ,2019 ,10 (3 ):187 -190 .
DOI:10.3969/j.issn.1674-7976.2019.03.007
[本文引用: 2]
[18]
TAKEICHI N Nominal flight time optimization for arrival time scheduling through estimation/resolution of delay accumulation
[J].Transportation Research Part C: Emerging Techno-logies ,2017 ,77 ,433 -443 .
DOI:10.1016/j.trc.2017.01.025
[本文引用: 1]
[19]
ZHANG Y C RONG S LI Q et al .Distributed flight routing and scheduling for air traffic flow management
[J].IEEE Trans.on Intelligent Transportation Systems ,2017 ,18 (10 ):2681 -2692 .
DOI:10.1109/TITS.2017.2657550
[本文引用: 1]
[20]
LIANG Z CHAOVALITWONGSE W A ELSAYED E A Sequence assignment model for the flight conflict resolution problem
[J].Transportation Science ,2014 ,48 (3 ):334 -350 .
DOI:10.1287/trsc.2013.0480
[本文引用: 1]
[21]
BENLIC U Heuristic search for allocation of slots at network level
[J].Transportation Research Part C: Emerging Technologies ,2018 ,86 (1 ):488 -509 .
[本文引用: 2]
[22]
ZHONG H GUAN W ZHANG W Y et al .A bi-objective integer programming model for partly-restricted flight departure scheduling
[J].PloS One ,2018 ,13 (5 ):e0196146 .
DOI:10.1371/journal.pone.0196146
[本文引用: 1]
[23]
ANDROUTSOPOULOS K N MANOUSAKIS E G MADAS M A Modeling and solving a bi-objective airport slot scheduling problem
[J].European Journal of Operational Research ,2020 ,284 (1 ):135 -151 .
DOI:10.1016/j.ejor.2019.12.008
[本文引用: 1]
[24]
JORGE D RIBEIRO N A ANTUNES A P Towards a decision-support tool for airport slot allocation: application to Guarulhos (Sao Paulo, Brazil)
[J].Journal of Air Transport Ma-nagement ,2021 ,93 (2 ):102048 .
[本文引用: 1]
[25]
FAIRBROTHER J ZOGRAFOS K G Optimal scheduling of slots with season segmentation
[J].European Journal of Operational Research ,2020 ,291 (3 ):961 -982 .
[本文引用: 1]
[26]
ZOGRAFOS K G JIANG Y A bi-objective efficiency-fairness model for scheduling slots at congested airports
[J].Transportation Research Part C: Emerging Technologies ,2019 ,102 (5 ):336 -350 .
[本文引用: 2]
[27]
FAIRBROTHER J ZOGRAFOS K G GLAZEBROOK K D A slot-scheduling mechanism at congested airports that incorporates efficiency, fairness, and airline preferences
[J].Transportation Science ,2020 ,54 (1 ):115 -138 .
DOI:10.1287/trsc.2019.0926
[本文引用: 1]
[28]
PELLEGRINIA P BOLIĆB T CASTELLI L et al .SOSTA: an effective model for the simultaneous optimization of airport slot allocation
[J].Transportation research Part E: Logistics and Transportation Review ,2017 ,99C (5 ):34 -53 .
URL
[本文引用: 1]
[29]
RIBEIRO N A JACQUILLAT A ANTUNES A P et al .Improving slot allocation at level 3 airports
[J].Transportation Research Part A: Policy and Practice ,2019 ,127 (9 ):32 -54 .
[本文引用: 1]
[30]
国家邮政局. 国家邮政局关于2021年快递服务满意度调查和时限准时率测试结果的通告[EB/OL]. [2022-04-15]. http://www.spb.gov.cn/gjyzj/c100009/c100010/202201/0ce493fa7228415e9a1e6e81998c4bbb.shtml .
[本文引用: 1]
State Post Bureau. Announcement of the state post bureau on the 2021 express service satisfaction survey and time-limi- ted on-time rate test results[EB/OL]. [2022-04-15]. http://www.spb.gov.cn/gjyzj/c100009/c100010/202201/0ce493fa7228415e9a1e6e81998c4bbb.shtml .
[本文引用: 1]
[31]
李翰 ,张洪海 ,张连东 ,等 .城市区域多物流无人机协同任务分配
[J].系统工程与电子技术 ,2021 ,43 (12 ):3594 -3602 .
URL
[本文引用: 2]
LI H ZHANG H H ZHANG L D et al .Multiple logistics unmanned aerial vehicle collaborative task allocation in urban areas
[J].Systems Engineering and Electronics ,2021 ,43 (12 ):3594 -3602 .
URL
[本文引用: 2]
1
... 国内外学者对城市低空物流无人机与飞行计划管理进行过研究.在城市空中交通发展方面, 文献[1 ]指出未来将会有大量电推进垂直起降型航空器服务于全球低空市场的发展.文献[2 ]认为未来城市空中交通的全球发展规模在2040年预计达到1.5万亿美元.文献[3 ]认为无人机将作为城市低空物流市场的主力服务于“最后一公里”配送, 预计2030年将满足5亿单运输需求.文献[4 ]分析了墨尔本的城市交通方式, 结果表明城市空中交通因其时间优势未来将拥有较大市场. ...
1
... 国内外学者对城市低空物流无人机与飞行计划管理进行过研究.在城市空中交通发展方面, 文献[1 ]指出未来将会有大量电推进垂直起降型航空器服务于全球低空市场的发展.文献[2 ]认为未来城市空中交通的全球发展规模在2040年预计达到1.5万亿美元.文献[3 ]认为无人机将作为城市低空物流市场的主力服务于“最后一公里”配送, 预计2030年将满足5亿单运输需求.文献[4 ]分析了墨尔本的城市交通方式, 结果表明城市空中交通因其时间优势未来将拥有较大市场. ...
1
... 国内外学者对城市低空物流无人机与飞行计划管理进行过研究.在城市空中交通发展方面, 文献[1 ]指出未来将会有大量电推进垂直起降型航空器服务于全球低空市场的发展.文献[2 ]认为未来城市空中交通的全球发展规模在2040年预计达到1.5万亿美元.文献[3 ]认为无人机将作为城市低空物流市场的主力服务于“最后一公里”配送, 预计2030年将满足5亿单运输需求.文献[4 ]分析了墨尔本的城市交通方式, 结果表明城市空中交通因其时间优势未来将拥有较大市场. ...
1
... 国内外学者对城市低空物流无人机与飞行计划管理进行过研究.在城市空中交通发展方面, 文献[1 ]指出未来将会有大量电推进垂直起降型航空器服务于全球低空市场的发展.文献[2 ]认为未来城市空中交通的全球发展规模在2040年预计达到1.5万亿美元.文献[3 ]认为无人机将作为城市低空物流市场的主力服务于“最后一公里”配送, 预计2030年将满足5亿单运输需求.文献[4 ]分析了墨尔本的城市交通方式, 结果表明城市空中交通因其时间优势未来将拥有较大市场. ...
A drone fleet model for last-mile distribution in disaster relief operations
2
2018
... 在低空物流无人机运行方面, 文献[5 ]考虑了无人机在人道主义物流最后一英里配送中的应用, 提出一种通过无人机将轻型救援物品(如疫苗、纯净水等)运送到受灾地区的优化模型.文献[6 ]提出利用无人机完成医疗保健运输更加及时、高效和经济, 设计了无人机医疗网络运输的决策模型.文献[7 ]关注了无人机在物流配送中区别于普通地面物流的基本特征, 考虑无人机飞行时间、装载能力、货物重量对飞行能力的影响, 提出一种混合整数线性规划公式和任务分配启发式算法, 并通过数值示例进行测试.文献[8 ]研究了无人机在人口稠密的城市环境中的运行风险, 利用空间模拟系统进行风险评估.文献[9 ]指出越来越多的物流公司都在研究使用无人机进行快递交付, 针对无人机投送的容量限制问题, 提出一种混合元启发式方法, 仿真结果证实了所提算法的有效性.文献[10 ]考虑权重系数、时间窗约束、无人机约束等建立了无人机物流任务分配模型, 采用改进粒子群优化算法求解, 仿真结果表明该算法能够有效解决无人机物流任务分配问题.文献[11 ]提出基于改进人工势场-快速扩展随机树算法, 以实现无人机在物流配送中准确、快速的路径规划.文献[12 ]使用牛顿运动定律和伽利略自由落体评估无人机碰撞概率密度, 通过路径规划保证无人机避开人口密集区域. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
1
... 在低空物流无人机运行方面, 文献[5 ]考虑了无人机在人道主义物流最后一英里配送中的应用, 提出一种通过无人机将轻型救援物品(如疫苗、纯净水等)运送到受灾地区的优化模型.文献[6 ]提出利用无人机完成医疗保健运输更加及时、高效和经济, 设计了无人机医疗网络运输的决策模型.文献[7 ]关注了无人机在物流配送中区别于普通地面物流的基本特征, 考虑无人机飞行时间、装载能力、货物重量对飞行能力的影响, 提出一种混合整数线性规划公式和任务分配启发式算法, 并通过数值示例进行测试.文献[8 ]研究了无人机在人口稠密的城市环境中的运行风险, 利用空间模拟系统进行风险评估.文献[9 ]指出越来越多的物流公司都在研究使用无人机进行快递交付, 针对无人机投送的容量限制问题, 提出一种混合元启发式方法, 仿真结果证实了所提算法的有效性.文献[10 ]考虑权重系数、时间窗约束、无人机约束等建立了无人机物流任务分配模型, 采用改进粒子群优化算法求解, 仿真结果表明该算法能够有效解决无人机物流任务分配问题.文献[11 ]提出基于改进人工势场-快速扩展随机树算法, 以实现无人机在物流配送中准确、快速的路径规划.文献[12 ]使用牛顿运动定律和伽利略自由落体评估无人机碰撞概率密度, 通过路径规划保证无人机避开人口密集区域. ...
Persistent UAV delivery logistics: MILP formulation and efficient heuristic
1
2018
... 在低空物流无人机运行方面, 文献[5 ]考虑了无人机在人道主义物流最后一英里配送中的应用, 提出一种通过无人机将轻型救援物品(如疫苗、纯净水等)运送到受灾地区的优化模型.文献[6 ]提出利用无人机完成医疗保健运输更加及时、高效和经济, 设计了无人机医疗网络运输的决策模型.文献[7 ]关注了无人机在物流配送中区别于普通地面物流的基本特征, 考虑无人机飞行时间、装载能力、货物重量对飞行能力的影响, 提出一种混合整数线性规划公式和任务分配启发式算法, 并通过数值示例进行测试.文献[8 ]研究了无人机在人口稠密的城市环境中的运行风险, 利用空间模拟系统进行风险评估.文献[9 ]指出越来越多的物流公司都在研究使用无人机进行快递交付, 针对无人机投送的容量限制问题, 提出一种混合元启发式方法, 仿真结果证实了所提算法的有效性.文献[10 ]考虑权重系数、时间窗约束、无人机约束等建立了无人机物流任务分配模型, 采用改进粒子群优化算法求解, 仿真结果表明该算法能够有效解决无人机物流任务分配问题.文献[11 ]提出基于改进人工势场-快速扩展随机树算法, 以实现无人机在物流配送中准确、快速的路径规划.文献[12 ]使用牛顿运动定律和伽利略自由落体评估无人机碰撞概率密度, 通过路径规划保证无人机避开人口密集区域. ...
1
... 在低空物流无人机运行方面, 文献[5 ]考虑了无人机在人道主义物流最后一英里配送中的应用, 提出一种通过无人机将轻型救援物品(如疫苗、纯净水等)运送到受灾地区的优化模型.文献[6 ]提出利用无人机完成医疗保健运输更加及时、高效和经济, 设计了无人机医疗网络运输的决策模型.文献[7 ]关注了无人机在物流配送中区别于普通地面物流的基本特征, 考虑无人机飞行时间、装载能力、货物重量对飞行能力的影响, 提出一种混合整数线性规划公式和任务分配启发式算法, 并通过数值示例进行测试.文献[8 ]研究了无人机在人口稠密的城市环境中的运行风险, 利用空间模拟系统进行风险评估.文献[9 ]指出越来越多的物流公司都在研究使用无人机进行快递交付, 针对无人机投送的容量限制问题, 提出一种混合元启发式方法, 仿真结果证实了所提算法的有效性.文献[10 ]考虑权重系数、时间窗约束、无人机约束等建立了无人机物流任务分配模型, 采用改进粒子群优化算法求解, 仿真结果表明该算法能够有效解决无人机物流任务分配问题.文献[11 ]提出基于改进人工势场-快速扩展随机树算法, 以实现无人机在物流配送中准确、快速的路径规划.文献[12 ]使用牛顿运动定律和伽利略自由落体评估无人机碰撞概率密度, 通过路径规划保证无人机避开人口密集区域. ...
1
... 在低空物流无人机运行方面, 文献[5 ]考虑了无人机在人道主义物流最后一英里配送中的应用, 提出一种通过无人机将轻型救援物品(如疫苗、纯净水等)运送到受灾地区的优化模型.文献[6 ]提出利用无人机完成医疗保健运输更加及时、高效和经济, 设计了无人机医疗网络运输的决策模型.文献[7 ]关注了无人机在物流配送中区别于普通地面物流的基本特征, 考虑无人机飞行时间、装载能力、货物重量对飞行能力的影响, 提出一种混合整数线性规划公式和任务分配启发式算法, 并通过数值示例进行测试.文献[8 ]研究了无人机在人口稠密的城市环境中的运行风险, 利用空间模拟系统进行风险评估.文献[9 ]指出越来越多的物流公司都在研究使用无人机进行快递交付, 针对无人机投送的容量限制问题, 提出一种混合元启发式方法, 仿真结果证实了所提算法的有效性.文献[10 ]考虑权重系数、时间窗约束、无人机约束等建立了无人机物流任务分配模型, 采用改进粒子群优化算法求解, 仿真结果表明该算法能够有效解决无人机物流任务分配问题.文献[11 ]提出基于改进人工势场-快速扩展随机树算法, 以实现无人机在物流配送中准确、快速的路径规划.文献[12 ]使用牛顿运动定律和伽利略自由落体评估无人机碰撞概率密度, 通过路径规划保证无人机避开人口密集区域. ...
1
... 在低空物流无人机运行方面, 文献[5 ]考虑了无人机在人道主义物流最后一英里配送中的应用, 提出一种通过无人机将轻型救援物品(如疫苗、纯净水等)运送到受灾地区的优化模型.文献[6 ]提出利用无人机完成医疗保健运输更加及时、高效和经济, 设计了无人机医疗网络运输的决策模型.文献[7 ]关注了无人机在物流配送中区别于普通地面物流的基本特征, 考虑无人机飞行时间、装载能力、货物重量对飞行能力的影响, 提出一种混合整数线性规划公式和任务分配启发式算法, 并通过数值示例进行测试.文献[8 ]研究了无人机在人口稠密的城市环境中的运行风险, 利用空间模拟系统进行风险评估.文献[9 ]指出越来越多的物流公司都在研究使用无人机进行快递交付, 针对无人机投送的容量限制问题, 提出一种混合元启发式方法, 仿真结果证实了所提算法的有效性.文献[10 ]考虑权重系数、时间窗约束、无人机约束等建立了无人机物流任务分配模型, 采用改进粒子群优化算法求解, 仿真结果表明该算法能够有效解决无人机物流任务分配问题.文献[11 ]提出基于改进人工势场-快速扩展随机树算法, 以实现无人机在物流配送中准确、快速的路径规划.文献[12 ]使用牛顿运动定律和伽利略自由落体评估无人机碰撞概率密度, 通过路径规划保证无人机避开人口密集区域. ...
Path planning of UAV delivery based on improved APF-RRT* algorithm
1
2020
... 在低空物流无人机运行方面, 文献[5 ]考虑了无人机在人道主义物流最后一英里配送中的应用, 提出一种通过无人机将轻型救援物品(如疫苗、纯净水等)运送到受灾地区的优化模型.文献[6 ]提出利用无人机完成医疗保健运输更加及时、高效和经济, 设计了无人机医疗网络运输的决策模型.文献[7 ]关注了无人机在物流配送中区别于普通地面物流的基本特征, 考虑无人机飞行时间、装载能力、货物重量对飞行能力的影响, 提出一种混合整数线性规划公式和任务分配启发式算法, 并通过数值示例进行测试.文献[8 ]研究了无人机在人口稠密的城市环境中的运行风险, 利用空间模拟系统进行风险评估.文献[9 ]指出越来越多的物流公司都在研究使用无人机进行快递交付, 针对无人机投送的容量限制问题, 提出一种混合元启发式方法, 仿真结果证实了所提算法的有效性.文献[10 ]考虑权重系数、时间窗约束、无人机约束等建立了无人机物流任务分配模型, 采用改进粒子群优化算法求解, 仿真结果表明该算法能够有效解决无人机物流任务分配问题.文献[11 ]提出基于改进人工势场-快速扩展随机树算法, 以实现无人机在物流配送中准确、快速的路径规划.文献[12 ]使用牛顿运动定律和伽利略自由落体评估无人机碰撞概率密度, 通过路径规划保证无人机避开人口密集区域. ...
Failure analysis for an unmanned aerial vehicle using safe path planning
2
2020
... 在低空物流无人机运行方面, 文献[5 ]考虑了无人机在人道主义物流最后一英里配送中的应用, 提出一种通过无人机将轻型救援物品(如疫苗、纯净水等)运送到受灾地区的优化模型.文献[6 ]提出利用无人机完成医疗保健运输更加及时、高效和经济, 设计了无人机医疗网络运输的决策模型.文献[7 ]关注了无人机在物流配送中区别于普通地面物流的基本特征, 考虑无人机飞行时间、装载能力、货物重量对飞行能力的影响, 提出一种混合整数线性规划公式和任务分配启发式算法, 并通过数值示例进行测试.文献[8 ]研究了无人机在人口稠密的城市环境中的运行风险, 利用空间模拟系统进行风险评估.文献[9 ]指出越来越多的物流公司都在研究使用无人机进行快递交付, 针对无人机投送的容量限制问题, 提出一种混合元启发式方法, 仿真结果证实了所提算法的有效性.文献[10 ]考虑权重系数、时间窗约束、无人机约束等建立了无人机物流任务分配模型, 采用改进粒子群优化算法求解, 仿真结果表明该算法能够有效解决无人机物流任务分配问题.文献[11 ]提出基于改进人工势场-快速扩展随机树算法, 以实现无人机在物流配送中准确、快速的路径规划.文献[12 ]使用牛顿运动定律和伽利略自由落体评估无人机碰撞概率密度, 通过路径规划保证无人机避开人口密集区域. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
2
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
2
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
2
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
低空通航飞行计划预先调配方法研究
2
2020
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
Research on pre-allocation method of low-altitude general aviation flight plan
2
2020
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
通用航空飞行计划处理系统的设计与实现
2
2019
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
Design and realization of general aviation flight plan system
2
2019
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
基于飞行计划集中处理的预战术航路飞行流量预测
2
2021
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
Flight flow prediction of pre-tactical routes based on centralized processing of flight plan
2
2021
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
Nominal flight time optimization for arrival time scheduling through estimation/resolution of delay accumulation
1
2017
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
Distributed flight routing and scheduling for air traffic flow management
1
2017
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
Sequence assignment model for the flight conflict resolution problem
1
2014
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
Heuristic search for allocation of slots at network level
2
2018
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
... 目前, 面向低空物流无人机的研究多集中于任务分配与路径规划[5 -12 ] , 面向飞行计划的研究集中于飞行调度[15 , 17 -21 ] 和管理系统[13 -14 , 16 ] , 但面向低空无人机运输中飞行计划调配流程的研究较少.无人机飞行计划预先调配可从高度、航路和时间的角度出发, 由于调整高度和航路存在局限, 一是城市低空可供调整的飞行空间有限, 往往不允许无人机产生大幅度空间变动; 二是无人机电量、承重等性能有限, 执行任务的空间变动会降低运输效率.因此, 本文研究基于实际运输需求, 从时间调整的角度出发, 以飞行计划成本最低为调配目标, 建立无人机飞行计划预先调配模型, 设计考虑综合优先级的飞行计划预先调配算法求解, 生成无冲突的时刻表, 为飞行任务排序后分配起飞时刻, 以实现飞行计划的预先调配. ...
A bi-objective integer programming model for partly-restricted flight departure scheduling
1
2018
... 在飞行计划调配方面, 文献[13 ]阐述了采用直接法和插值法划设调配区域的预先飞行调配系统, 辅助管制员自动生成调配建议.文献[14 ]设计了由安全高效的空域调度系统构成的路径规划模型和路径查找算法, 可避免航班申请的冲突.文献[15 ]考虑综合优先级的影响建立飞行计划调配模型, 提出一种飞行计划调配方法.文献[16 ]研究了一种飞行计划调配系统来动态申请、批复和监视空域, 通航用户依托系统可与管理部门进行信息交流.文献[17 ]提出一种基于飞行计划集中处理的预战术飞行流量预测方法, 利用飞行计划预测航空器航迹进而预测航路点流量.文献[18 ]以网络交通流的运营成本最小为目标, 通过调配飞行计划估计航空器最佳计划到达时间.文献[19 ]提出一种空中交通航路系统模型以解决飞行中调度问题.文献[20 ]提出一种飞行序列分配模型, 以解决不同航空公司飞行计划在安全标准时间表上的冲突.文献[21 ]针对协调拥挤机场网络的时刻分配问题, 考虑时刻请求的优先级、最短周转时间等, 提出一种启发式方法为每个机场生成可行且连贯的时隙.文献[22 ]考虑到高峰时段低优先级机场需要让位高优先级机场的出发活动, 提出一种双目标整数规划模型, 以解决较低优先级航班的起飞调度问题. ...
Modeling and solving a bi-objective airport slot scheduling problem
1
2020
... 借鉴航班时刻分配的有关研究, 文献[23 ]分析了双目标资源约束调度来解决战略机场时刻分配问题, 提出一种新型混合启发式算法, 并以希腊机场的实际时隙数据验证了所提算法的准确性.文献[24 ]介绍了一种协助人工进行初始时隙分配的优化决策支持工具, 该工具在可接受的时间内生成有效的时隙解决航班分配问题.文献[25 ]研究了阻塞缓解策略, 提出一种航班时隙分配模型和解决方案, 通过调度时刻来缓解机场拥堵.文献[26 ]提出一种考虑时刻调度效率和公平性的双目标机场时刻调度模型, 研究了考虑历史时隙使用权和不考虑历史时隙使用权的机制下时隙调度效率-公平的权衡, 以实现航班时隙调度.文献[27 ]在文献[26 ]的基础上提出了考虑效率、公平性和航空公司偏好的多目标两阶段时刻分配机制.文献[28 ]提出一种整数线性规划模型, 通过周转时间限制飞机轮转, 用于在欧洲范围内优化机场时刻分配.文献[29 ]提出一种符合全球航班时刻指南的优化模型, 将机场时刻分配给航空公司. ...
Towards a decision-support tool for airport slot allocation: application to Guarulhos (Sao Paulo, Brazil)
1
2021
... 借鉴航班时刻分配的有关研究, 文献[23 ]分析了双目标资源约束调度来解决战略机场时刻分配问题, 提出一种新型混合启发式算法, 并以希腊机场的实际时隙数据验证了所提算法的准确性.文献[24 ]介绍了一种协助人工进行初始时隙分配的优化决策支持工具, 该工具在可接受的时间内生成有效的时隙解决航班分配问题.文献[25 ]研究了阻塞缓解策略, 提出一种航班时隙分配模型和解决方案, 通过调度时刻来缓解机场拥堵.文献[26 ]提出一种考虑时刻调度效率和公平性的双目标机场时刻调度模型, 研究了考虑历史时隙使用权和不考虑历史时隙使用权的机制下时隙调度效率-公平的权衡, 以实现航班时隙调度.文献[27 ]在文献[26 ]的基础上提出了考虑效率、公平性和航空公司偏好的多目标两阶段时刻分配机制.文献[28 ]提出一种整数线性规划模型, 通过周转时间限制飞机轮转, 用于在欧洲范围内优化机场时刻分配.文献[29 ]提出一种符合全球航班时刻指南的优化模型, 将机场时刻分配给航空公司. ...
Optimal scheduling of slots with season segmentation
1
2020
... 借鉴航班时刻分配的有关研究, 文献[23 ]分析了双目标资源约束调度来解决战略机场时刻分配问题, 提出一种新型混合启发式算法, 并以希腊机场的实际时隙数据验证了所提算法的准确性.文献[24 ]介绍了一种协助人工进行初始时隙分配的优化决策支持工具, 该工具在可接受的时间内生成有效的时隙解决航班分配问题.文献[25 ]研究了阻塞缓解策略, 提出一种航班时隙分配模型和解决方案, 通过调度时刻来缓解机场拥堵.文献[26 ]提出一种考虑时刻调度效率和公平性的双目标机场时刻调度模型, 研究了考虑历史时隙使用权和不考虑历史时隙使用权的机制下时隙调度效率-公平的权衡, 以实现航班时隙调度.文献[27 ]在文献[26 ]的基础上提出了考虑效率、公平性和航空公司偏好的多目标两阶段时刻分配机制.文献[28 ]提出一种整数线性规划模型, 通过周转时间限制飞机轮转, 用于在欧洲范围内优化机场时刻分配.文献[29 ]提出一种符合全球航班时刻指南的优化模型, 将机场时刻分配给航空公司. ...
A bi-objective efficiency-fairness model for scheduling slots at congested airports
2
2019
... 借鉴航班时刻分配的有关研究, 文献[23 ]分析了双目标资源约束调度来解决战略机场时刻分配问题, 提出一种新型混合启发式算法, 并以希腊机场的实际时隙数据验证了所提算法的准确性.文献[24 ]介绍了一种协助人工进行初始时隙分配的优化决策支持工具, 该工具在可接受的时间内生成有效的时隙解决航班分配问题.文献[25 ]研究了阻塞缓解策略, 提出一种航班时隙分配模型和解决方案, 通过调度时刻来缓解机场拥堵.文献[26 ]提出一种考虑时刻调度效率和公平性的双目标机场时刻调度模型, 研究了考虑历史时隙使用权和不考虑历史时隙使用权的机制下时隙调度效率-公平的权衡, 以实现航班时隙调度.文献[27 ]在文献[26 ]的基础上提出了考虑效率、公平性和航空公司偏好的多目标两阶段时刻分配机制.文献[28 ]提出一种整数线性规划模型, 通过周转时间限制飞机轮转, 用于在欧洲范围内优化机场时刻分配.文献[29 ]提出一种符合全球航班时刻指南的优化模型, 将机场时刻分配给航空公司. ...
... ]在文献[26 ]的基础上提出了考虑效率、公平性和航空公司偏好的多目标两阶段时刻分配机制.文献[28 ]提出一种整数线性规划模型, 通过周转时间限制飞机轮转, 用于在欧洲范围内优化机场时刻分配.文献[29 ]提出一种符合全球航班时刻指南的优化模型, 将机场时刻分配给航空公司. ...
A slot-scheduling mechanism at congested airports that incorporates efficiency, fairness, and airline preferences
1
2020
... 借鉴航班时刻分配的有关研究, 文献[23 ]分析了双目标资源约束调度来解决战略机场时刻分配问题, 提出一种新型混合启发式算法, 并以希腊机场的实际时隙数据验证了所提算法的准确性.文献[24 ]介绍了一种协助人工进行初始时隙分配的优化决策支持工具, 该工具在可接受的时间内生成有效的时隙解决航班分配问题.文献[25 ]研究了阻塞缓解策略, 提出一种航班时隙分配模型和解决方案, 通过调度时刻来缓解机场拥堵.文献[26 ]提出一种考虑时刻调度效率和公平性的双目标机场时刻调度模型, 研究了考虑历史时隙使用权和不考虑历史时隙使用权的机制下时隙调度效率-公平的权衡, 以实现航班时隙调度.文献[27 ]在文献[26 ]的基础上提出了考虑效率、公平性和航空公司偏好的多目标两阶段时刻分配机制.文献[28 ]提出一种整数线性规划模型, 通过周转时间限制飞机轮转, 用于在欧洲范围内优化机场时刻分配.文献[29 ]提出一种符合全球航班时刻指南的优化模型, 将机场时刻分配给航空公司. ...
SOSTA: an effective model for the simultaneous optimization of airport slot allocation
1
2017
... 借鉴航班时刻分配的有关研究, 文献[23 ]分析了双目标资源约束调度来解决战略机场时刻分配问题, 提出一种新型混合启发式算法, 并以希腊机场的实际时隙数据验证了所提算法的准确性.文献[24 ]介绍了一种协助人工进行初始时隙分配的优化决策支持工具, 该工具在可接受的时间内生成有效的时隙解决航班分配问题.文献[25 ]研究了阻塞缓解策略, 提出一种航班时隙分配模型和解决方案, 通过调度时刻来缓解机场拥堵.文献[26 ]提出一种考虑时刻调度效率和公平性的双目标机场时刻调度模型, 研究了考虑历史时隙使用权和不考虑历史时隙使用权的机制下时隙调度效率-公平的权衡, 以实现航班时隙调度.文献[27 ]在文献[26 ]的基础上提出了考虑效率、公平性和航空公司偏好的多目标两阶段时刻分配机制.文献[28 ]提出一种整数线性规划模型, 通过周转时间限制飞机轮转, 用于在欧洲范围内优化机场时刻分配.文献[29 ]提出一种符合全球航班时刻指南的优化模型, 将机场时刻分配给航空公司. ...
Improving slot allocation at level 3 airports
1
2019
... 借鉴航班时刻分配的有关研究, 文献[23 ]分析了双目标资源约束调度来解决战略机场时刻分配问题, 提出一种新型混合启发式算法, 并以希腊机场的实际时隙数据验证了所提算法的准确性.文献[24 ]介绍了一种协助人工进行初始时隙分配的优化决策支持工具, 该工具在可接受的时间内生成有效的时隙解决航班分配问题.文献[25 ]研究了阻塞缓解策略, 提出一种航班时隙分配模型和解决方案, 通过调度时刻来缓解机场拥堵.文献[26 ]提出一种考虑时刻调度效率和公平性的双目标机场时刻调度模型, 研究了考虑历史时隙使用权和不考虑历史时隙使用权的机制下时隙调度效率-公平的权衡, 以实现航班时隙调度.文献[27 ]在文献[26 ]的基础上提出了考虑效率、公平性和航空公司偏好的多目标两阶段时刻分配机制.文献[28 ]提出一种整数线性规划模型, 通过周转时间限制飞机轮转, 用于在欧洲范围内优化机场时刻分配.文献[29 ]提出一种符合全球航班时刻指南的优化模型, 将机场时刻分配给航空公司. ...
1
... 飞行计划调配优先级主要包括货物类型优先、物流公司优先和配送时间优先.货物类型优先是指为紧急程度高的任务优先分配时刻, 物流公司优先是指为顾客满意度高[30 ] 的物流公司优先分配时刻, 配送时间优先是指为顾客期望送达时间早的任务优先分配时刻.因此, 本文提出的综合优先级由货物类型优先级、物流公司优先级和配送时间优先级这三部分组成, 优先级取值由飞行任务决定, 分别给予每个部分不同的权重.在进行无人机飞行计划调配时, 每条任务的综合优先级λ i
1
... 飞行计划调配优先级主要包括货物类型优先、物流公司优先和配送时间优先.货物类型优先是指为紧急程度高的任务优先分配时刻, 物流公司优先是指为顾客满意度高[30 ] 的物流公司优先分配时刻, 配送时间优先是指为顾客期望送达时间早的任务优先分配时刻.因此, 本文提出的综合优先级由货物类型优先级、物流公司优先级和配送时间优先级这三部分组成, 优先级取值由飞行任务决定, 分别给予每个部分不同的权重.在进行无人机飞行计划调配时, 每条任务的综合优先级λ i
城市区域多物流无人机协同任务分配
2
2021
... 运输成本是指无人机在配送过程中产生的费用, 包括电池能耗、折旧维护等费用[31 ] , 表达式为 ...
... 为验证本文模型和方法的有效性, 基于Python3.8仿真模拟平台进行实例验证, 由于当前物流无人机末端配送基础设施建设不全面, 缺乏实际案例数据, 为尽量真实模拟运输过程, 参考文献[31 ]设置仿真参数.选取南航江宁校区驿站配送点, 08:00至10:00期间任务执行完毕, 相关参数设置如表 1 所示. ...
Multiple logistics unmanned aerial vehicle collaborative task allocation in urban areas
2
2021
... 运输成本是指无人机在配送过程中产生的费用, 包括电池能耗、折旧维护等费用[31 ] , 表达式为 ...
... 为验证本文模型和方法的有效性, 基于Python3.8仿真模拟平台进行实例验证, 由于当前物流无人机末端配送基础设施建设不全面, 缺乏实际案例数据, 为尽量真实模拟运输过程, 参考文献[31 ]设置仿真参数.选取南航江宁校区驿站配送点, 08:00至10:00期间任务执行完毕, 相关参数设置如表 1 所示. ...