0 引言
考虑到任务分配和航迹规划之间的耦合关系, Gottlieb等人在任务分配中考虑目标价值和无人机到达目标时间, 航迹则由Dubins路径长度表示[6]。Kim等人考虑了目标的资源需求和无人机资源约束, 采用无人机联盟的方式同时攻击目标[7]。Yao等人使用A*算法估计无人机到达目标的折线距离, 并将其作为目标函数的代价考虑[8]。Mana-thara等人在各无人机规划航迹之后, 当无人机之间由于避碰机制发生航迹偏移后, 通过仅调整速度实现同时到达[9-10]。部分研究者为集群个体规划等长航迹, 各无人机以相同速度等速航行[11-12]。严飞等人考虑目标函数中的收益和航迹代价影响, 提出了一种基于合同网的任务分配方法[13]。Mclain等人基于Voronoi图生成多条备选路径后, 采用协调变量和协调函数[14]的方法为备选路径赋予合适的速度值, 实现同时到达[15]。Shima等人通过使用旅行推销员问题求解器, 基于欧几里得距离对一组任务进行排序来解决同时到达问题[16]。袁利平等人考虑到战场环境的动态性和不确定性以及无人机自身的特点, 提出一种适用于多无人机同时到达的分散化控制方法, 其内容包括仅依靠局部信息交互的分散化控制结构和基于一致性算法的分散化控制策略, 但由于仅采用速度调整的方式, 无人机的航行速度极易达到饱和[17]。集群弹药大多以固定翼无人机为平台, 故上述多数研究者在解决同时到达问题中都使用了Dubins航迹规划[18]。由于其路径由直线段和曲线段构成, 更为贴合固定翼无人机的控制机理。然而, 大多研究者们仅仅采用简单的距离代价融入任务分配的目标函数中, 导致只能采用等长航迹的方法完成同时到达任务, 造成打击时间过长的情况。减少集群的打击时间可以采用变速的方法, 如何将速度和路径信息融入到任务分配中为该问题的关键。
本文针对固定翼集群弹药协同打击地面目标展开研究, 采用双层优化的方法将任务分配和航迹规划看作一个整体, 并提出了一种基于Dubins航迹规划的多模式规划方法, 在保证同时到达的前提下, 达到集群打击效能的最优。本研究主要有以下创新点: ①采用双层优化处理上述问题, 相较于解耦的处理方式更易得到全局最优解; ②将速度变量引入航迹规划中, 与传统增加航行路径的规划相比, 其路径长度与航行时间更优; ③由于弹药具有航行速度约束, 设计了一种多模式的路径规划方法, 保证极端环境下任务的完成。
本文安排如下: 第1节对战场环境的任务需求进行描述和对集群弹药任务规划进行建模; 第2节介绍时间协同攻击规划算法各单元以及内部的数据流向; 第3节在多种不同的战场环境中对时间协同攻击规划算法进行实验验证; 第4节对本文进行总结并得出结论。
1 问题建模
1.1 现代战场环境建模
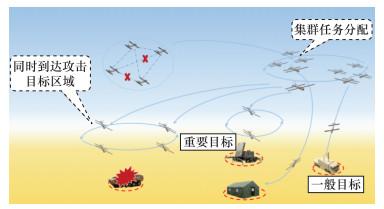
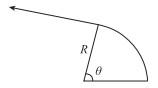
本文考虑固定翼集群弹药协同打击环境中的地面目标, 如图 1所示。集群弹药在发现地面群体目标后, 进行协同攻击任务规划, 完成同时打击目标任务。其中, 集群弹药的作战场景范围为[Xleft, Xright]×[Ylower, Yupper], 集群弹药集合为U={U1, U2, …, UM}, 任务目标集合为T={T1, T2…, TN}, 其中M和N分别表示集群弹药规模和任务目标个数。
图1
针对每个目标Tj∈T, 定义其位置posj, 价值wj表示选择目标时的优先级, 价值越高的目标在分配时被更优先考虑, 防御能力dj表示在此目标所需要的打击能力要求。针对每枚弹药Ui∈U, 将弹药的航迹分隔为K个航点, 定义其各航点位置pik、航点速度vik, 航向headi。
在本文考虑目标仅需要一种打击能力, 且弹药能力单一, 所以任务目标防御能力dj可以简单地理解为完成任务所需的弹药数量。集群弹药任务分配中, 对于每个目标需求能力的满足程度为一个重要指标, 且每个目标个体都有其自身的价值, 也就是攻击时的优先顺序。
1.2 协同打击问题建模
本文基于双层优化模型理论, 对集群弹药协同攻击地面群体目标进行建模。其中, 底层优化问题为各弹药的航迹规划问题, 顶层优化问题为群体地面目标的分配。
式(1)中, fupper表示上层优化的目标函数; valuej表示指定目标Tj完成同时打击任务的收益; timej表示同时打击指定目标Tj的代价。式(2)和式(3)为上层优化的约束, 其中xij为任务分配的决策变量, xij=1时, 表示弹药Ui分配给指定目标Tj; 否则, xij=0表示弹药Ui未分配给指定目标Tj。vik为航迹规划中每个航点的速度变量, 其大小处于最小航行速度vmin和最大航行速度vmax之间。
式(4)中, flower表示下层优化的目标函数; len(pik)表示弹药Ui规划出的第k个航点的长度代价。式(5)~式(7)为下层优化的约束, 其中pikX表示航点pik的X坐标, pikY表示航点pik的Y坐标。
2 时间协同攻击规划算法
2.1 任务规划系统架构
在时间协同攻击规划算法中, 每枚弹药都具有相同的处理单元, 各弹药根据各自的处理单元进行决策, 每个决策周期包含以下过程。
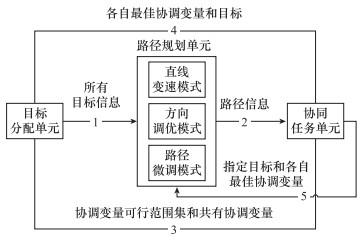
首先, 基于弹药自身的感知能力, 弹药所能感知的环境信息包括友方弹药、地面目标以及障碍物的位置及速度信息等, 由此获得环境的原始信息。获取环境信息后, 集群弹药依赖于自身的协同任务单元、路径规划单元和目标分配单元之间相互协同, 最终共同为弹药生成对指定目标的最优航迹。集群弹药的任务规划框架如图 2所示。其中, 路径规划单元生成从指定弹药到特定目标的最优路径, 并根据任务协同单元得到协调变量, 将相应的航行速度赋予最优路径中的每一个航点。路径规划单元返回关于每条路径的信息。目标分配单元和协同任务单元都调用路径规划单元。目标分配单元是为每枚弹药分配一个特定目标。协同任务单元的作用是确保当目标分配单元将多枚弹药分配给同一目标或目标群体时, 集群弹药同时到达目标攻击位置。
图2
2.2 决策流程
首先, 路径规划单元从目标分配单元中得到目标位置, 从而得到各弹药到目标的最优路径, 各路径点表示为pik, 最终将所得到的航点发送到协同任务单元。
随后, 协同任务单元收到来自路径规划单元的航点信息后, 根据弹药自身的可行航行速度范围, 给各路径点赋予航行速度, 并用vik表示, 从而得到完整的各路径点信息(pik, vik), 并根据协调函数将各路径信息转化为一维的协调变量, 用Time来表示, 将所得的协调变量可行范围集TIMEij和共有协调变量Time*发送给目标分配单元。
接下来, 目标分配单元收到来自协同任务单元发送的协调变量后, 根据内部的评价函数为每枚弹药决策出其任务目标和对应的航点速度, 根据共有的协调函数Time*, 决策出各自的最佳协调变量并发送到协同任务单元。
最终, 协同任务单元把各自的最佳协调变量和指定目标转发给路径规划单元, 并由路径规划单元规划完整的路径点信息。
2.3 路径规划单元
集群弹药打击地面目标时, 由于探测范围远大于打击范围, 发现目标后可充分地调整飞行航向及航迹长度。因此, 路径规划单元的主要功能是生成最优的可行航迹, 并及时响应协同任务单元的指令进行路径的微调。根据弹药的飞行特点, 将整条航迹简单地分为盘旋航迹和直线航迹, 因此Dubins航迹规划中的RS和LS更为适用。其中, R为right, L为left, S为straight; RS表示航迹由向右的圆弧和直线构成, LS则表示航迹由向左的圆弧和直线构成。
2.3.1 多模式路径规划
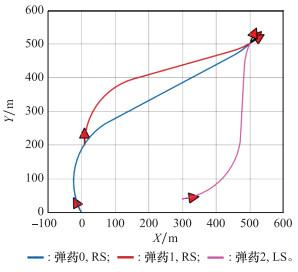
为了实现同时打击的任务需求, 如图 3所示, 蓝红粉分别表示不同的弹药航迹, 图标中LS和RS表示弹药生成Dubins航迹类型。本文设计了3种模式来规划满足要求的飞行航迹。
图3
(1) 直线加速模式
当弹药平飞时, 其受力平衡, 处于稳定状态。根据弹药的巡航速度范围, 在此状态下对其速度进行调整。
(2) 方向调优模式
当弹药收到航迹规划指令时, 其初始的航向与目标位置均有一定的角度偏差。在进入平飞状态前, 对弹药的航向进行调整, 规划部分盘旋航迹来满足弹药航向的需求。
(3) 路径微调模式
当仅通过速度调整无法满足同时打击的任务需求时, 协同任务单元将会再次调用路径规划单元, 对当前航迹重新进行规划, 为满足弹药的动力学约束, 采用改变盘旋航迹半径的方法, 增加一定的盘旋航迹来保证航行时间的一致性。但值得注意的是: 此模式仅可增加部分路径来满足航行时间要求, 若航行时间相差过大, 该模式也将失效。
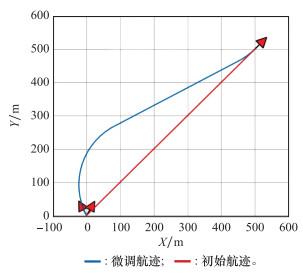
路径微调模式的路径调整如图 4所示, 弹药初始位置为(0, 0), 目标位置为(500, 500), 当初始红色航迹无法满足要求时, 路径微调模式将路径重新规划为蓝色航迹。
图4
2.3.2 航迹估算
本文将弹药Ui规划出的航迹用K个航点pik表示, 估算pik的航迹长度:
式中: R表示盘旋航迹的半径。
可得出路径规划中的目标函数:
式中: flower表示所有弹药规划航迹的总长度。
2.4 协同任务单元
单枚弹药难以彻底摧毁地面目标, 故需要组成满足作战能力的团队来保证任务的完成。团队成员协同打击地面目标时, 各成员同时到达攻击范围的时机至关重要, 就需要所有个体同时对所探测到的目标进行航迹规划。根据战场态势和弹药动态能力确定作战团队的最佳同时到达时间为任务的关键所在。协同任务单元为各弹药航迹决策出共有的协调函数, 集群中的个体根据协调函数, 规划出具有速度信息的最优航迹, 使得集群同时到达指定地面目标区域。
协同任务单元接收到来自路径规划单元的航迹信息后, 需要根据弹药动力学约束为每枚弹药的每条航迹拟定合适的航行速度。弹药Ui对探测到目标的候选航迹由航点pik和弹药航行速度vik表示, 故弹药Ui到达特定目标Tj的航行时间可表示为具有航行速度的航迹函数:
式中: Sij为协调函数。由于要使得多枚弹药最终同时到达指定目标, 就必须要进行相互协商, 与友方个体之间交换候选路径信息。由于各弹药的候选航迹和速度信息各不相同, 弹间相互传递pik和vik的方法较为低效, 故采用上述更为有效的信息, 即协调函数Sij。
协调变量Timeij由协调函数Sij决定。根据路径规划单元确定的候选路径和弹药航行速度的可行范围, 可确定作战团队中每枚弹药协调变量可行范围集TIMEij。由于路径规划单元采用多模式的规划方法, 弹药的完整航迹可分为直线航迹和盘旋航迹。故弹药Ui到达地面目标Tj的协调变量表示为
式中: Timestraightij表示弹药Ui对地面目标Tj直线航迹的协调变量;Timecircleij则表示其盘旋航迹的协调变量。
2.4.1 直线航迹协调变量计算
式中: Vi表示当前航点到下一航点的航行速度;Lenstraight表示速度恒定为Vi时的航迹长度。
2.4.2 盘旋航迹协调变量计算
式中: θ表示盘旋航迹的对应旋转角度;Vcircle表示弹药盘旋模式的恒定航行速度,盘旋航迹如图 5所示。
图5
弹药Ui对指定目标Tj的协调变量Timeij的可行范围集用TIMEij表示, 该范围集在集群个体之间相互交换, 最终被目标分配单元接收, 并完成打击目标的分配、航行速度以及航迹的选择。
协同任务单元通过要求每枚弹药匹配共有的协调变量Time*的团队最佳值, 得以确保集群弹药间的合作。
确定共有协调变量Time*有两种方案如下。
(1) 选用到达目标航迹最短的弹药为基准, 航行时间选为最慢航行速度时的到达时间为Time*。
(2) 选用到达目标航迹最长的弹药为基准, 航行时间选为最快航行速度时的到达时间为Time*。
协同打击地面目标时, 过长的航行时间将会增加集群被雷达探测到的风险, 故第(1)种方案更为贴合真实战场要求。
为了确保协同打击任务的完成, 所得的共有协调变量Time*必须在到达同一目标成员的可行范围集TIMEij中, 即Time*∈TIMEij。若其不满足此约束, 将启用路径规划单元中路径微调模式, 增加盘旋航迹的半径来满足任务约束。
一旦协同任务单元收到从目标分配单元发送的目标信息和协调变量Timeij后, 将该变量转发给路径规划单元, 每枚弹药必须确定要选择的最佳航迹pik和适当的航行速度vik, 匹配自身的值Timeij。协同任务单元仅通过搜索协调变量可行范围集TIMEij, 而不是路径规划单元的原始航迹信息(pik, vik), 极大简化了优化问题的复杂度。例如, 在协调同时到达问题中, 协调变量Time是一维的变量, 而原始航迹信息的维数要高得多。但实际上, 确定共有协调变量Time*到指定目标Tj的最佳路径, 只需在协同任务单元中查找协调变量可行范围集TIMEij即可。
2.5 目标分配单元
将航迹的协调变量等时间约束变量纳入任务分配的考虑范畴, 以保证同时达到任务完成的前提下, 最大化作战效能。根据上述任务需求, 集群弹药分配目标有两个考虑的指标:
(1) 对指定目标最小化各协调变量的差值;
(2) 最大限度增加每个目标所分配的弹药个数。
将以上两个指标分别用同时达到time以及饱和攻击value表示。其中,同时达到是必要目标, 饱和攻击则是集群目标。
2.5.1 必要目标
使用路径规划单元生成到每个目标的最优航迹起初是没有速度变量的, 在协同任务单元之中将航迹中的每个航点都赋予合理的速度值, 并经过协调函数的计算简化为一维变量协调变量。在任务分配的过程中, 若要满足于同时到达特定目标的约束, 需使得各枚弹药的协调变量Timeij尽可能地接近。
由于在协调任务单元中对于航迹中每一个航点的速度均进行合理的选取且确定了对指定目标的共有协调变量Time*, 根据自身协调变量和共有协调变量的差值timej:
表示从协同任务单元收到的协调变量可行范围集TIMEij中,找到与共有的协调变量Time*最接近的航迹。
2.5.2 集群目标
从饱和攻击价值函数value(·)的角度来看, 分配给指定目标的弹药数量越多越好。由一个值来表示每个指定目标的团队规模, 可使用一个单调递增的函数来表示。团队成员数量在达到任务需求前, 该函数的值急剧增加, 表明最小可接受团队规模为任务的需求数量。设Uj={U1, U2, …, UMj}表示分配给指定目标Tj的一组弹药; Uij是分配给制定目标Tj的弹药。函数valuej可表示为
式中: Mj表示分配给指定目标Tj的弹药数量, Mj=∑i=1Mxij; dj表示指定目标Tj的防御能力, 即完成任务需要的弹药数量。
设Tassignment={T1, T2, …, Tna}表示在分配中被分配到弹药的所有目标集合, 那么最终的分配效能:
该值取每个团队规模值与指定目标集Tassignment的乘积, 该函数可以让不满足饱和攻击的目标显著降低总体任务的价值。
但是, value仅解决了在团队目标为主的需求, 也就是在为每个目标分配足够数量弹药的同时, 尽可能地为战场所有目标分配弹药。若要满足协同打击任务, 需着重考虑同时达到time。
最终, 提出了统一的分配指标fupper, 来平衡集群目标和必要目标之间的需求:
该算法从算法架构、航迹生成和协同方案等多个方面考虑。在算法架构方面, 并没有将任务分配和航迹规划解耦为两个独立的问题来求解, 而是采用双层优化的方法将该问题看作一个整体, 避免了解耦而造成的局部最优; 在航迹生成方面, 多模式的航迹规划方法在仅采用速度调整无法满足任务要求时, 采用增加转弯半径的方式延长路径长度, 保证了任务的完成; 在协同方案方面, 采用速度调整方式, 与传统方式中采用延长路径的方式相比, 保证了任务完成时间的最优性。
3 仿真试验与结果分析
3.1 任务场景设置
本文任务场景设置(如初始位置、初始航向、初始速度等) 环境参数如表 1所示。任务区域大小为2 km×2 km, 执行协同打击任务的弹药选用固定翼巡飞弹。
表1 弹药初始条件
Table 1
| 弹药 | 初始位置/m | 初始航向/(°) | 初始速度/(m/s) |
| 1 | (0, 0) | 134 | 30 |
| 2 | (10, 200) | 33 | 30 |
| 3 | (300, 40) | -25 | 30 |
| 4 | (800, 500) | 0 | 30 |
| 5 | (700, 700) | 25 | 30 |
| 6 | (1 500, 1 000) | 103 | 30 |
| 7 | (750, 1 250) | 0 | 30 |
| 8 | (1 000, 1 100) | 20 | 30 |
| 9 | (900, 1 500) | 76 | 30 |
| 10 | (80, 70) | 0 | 30 |
| 11 | (1 100, 1 500) | 33 | 30 |
| 12 | (600, 600) | 45 | 30 |
3.2 算例设置和评价指标
3.2.1 算例设置
本文从目标位置、目标价值、防御能力等不同战场环境因素考虑, 设计了5种算例(每个算例分别进行10次实验)来测试算法性能, 具体设置如表 2所示。本文从任务完成时间和打击效能等两个方面对该算法性能进行评估。
表2 算例设置
Table 2
| 算例 | 目标数量 | 目标位置 | 目标价值 | 防御能力 |
| 1 | 3 | (500, 500)、(1 000, 1 000)、(1 500, 1 500) | 90、90、90 | 3、3、3 |
| 2 | 3 | (500, 500)、(1 000, 1 000)、(1 500, 1 500) | 90、70、50 | 3、3、3 |
| 3 | 3 | (500, 500)、(1 000, 1 000)、(1 500, 1 500) | 90、90、90 | 4、3、2 |
| 4 | 3 | (500, 500)、(800, 800)、(1 100, 1 100) | 90、90、90 | 3、3、3 |
| 5 | 3 | (500, 500)、(1 000, 1 000)、(1 500, 1 500) | 90、70、50 | 4、4、4 |
3.2.2 评价指标
本文从任务完成时间、打击效能等两个方面对该算法性能进行评估。
对于时间消耗, 将从目标平均打击时间和单个目标打击时间两个维度分别进行比较。
(1) 目标平均打击时间
协同打击地面目标执行任务的时间越长, 弹药暴露的风险越大, 导致整个任务失败的概率越大。提出目标平均打击时间指标Timeave:
式中: Mj表示同时打击指定目标Tj的弹药成员数量; timeij表示弹药Ui对指定目标Tj的实验航行时间。
(2) 单目标打击时间差
对于单个目标, 协同打击同一目标的弹药团队中, 成员到达该目标的飞行耗时越接近, 打击效果越好。提出单目标打击时间差Timelagj:
式中: Timefirstarrive表示最先到达指定目标弹药的飞行耗时; Timelastarrive表示最后到达指定目标弹药的飞行耗时。
(3) 打击效能
协同打击地面目标存在优先级的情形下, 需要在战场资源有限的情形下, 尽可能地提高同时打击任务完成度。由此,提出打击效能评估指标:
式中: ωj表示指定目标Tj的战场价值, χj表示指定目标Tj在打击任务中及时打击的弹药数量; xij为弹药打击时效指标, 表示弹药Ui打击目标任务Tj是否及时, 若弹药Ui与首先到达目标的弹药时间差小于6 s, xij=1;否则, xij=0。(考虑到敌方目标做出防御和反击指令需要时间, 经查阅资料, 确定此时间为6 s较为合适)Mj表示分配给指定目标Tj的弹药数量。
3.3 数值实验和结果比较
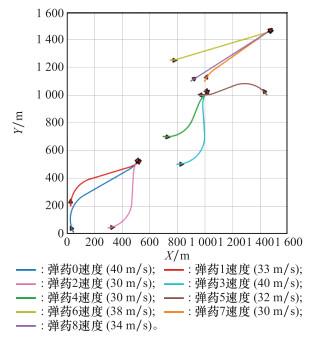
图6
3.3.1 任务时间消耗
任务时间消耗方面, 每个算例下3种算法的目标平均打击时间Timeave如表 3所示。其中, 加粗的数值为每个算例下每个目标的最小平均打击时间, 表格中的数值均为10次实验的平均值。可以看出, 同种算例的情况下, 3种算法的目标平均打击时间Timeave表现如下: 时间协同攻击规划算法打击时间最短, 最优协调路径规划打击时间最长, 一致性交汇算法打击时间介于两者之间。正是由于采用控制速度和改变航迹长度的规划方法, 相较于单一的等长航迹的方法, 可以具备更佳的打击时效性。
表3 目标平均打击时间
Table 3
| 算例 | 时间协同攻击规划 | 最优协调路径规划[12] | 一致性交汇算法[9] | ||||||||
| 目标1 | 目标2 | 目标3 | 目标1 | 目标2 | 目标3 | 目标1 | 目标2 | 目标3 | |||
| 1 | 15.412 | 18.323 | 13.719 | 47.761 | 46.155 | 63.825 | 39.376 | 40.318 | 14.654 | ||
| 2 | 18.323 | 15.412 | 13.719 | 46.155 | 47.761 | 63.825 | 46.926 | 15.453 | 63.448 | ||
| 3 | 18.678 | 15.412 | 12.975 | 47.276 | 46.155 | 63.487 | 38.625 | 40.318 | 20.205 | ||
| 4 | 26.278 | 18.323 | 18.812 | 47.935 | 49.552 | 47.265 | 39.376 | 36.599 | 44.984 | ||
| 5 | 18.678 | 15.441 | 14.766 | 45.662 | 52.674 | 45.579 | 22.511 | 25.000 | 32.269 | ||
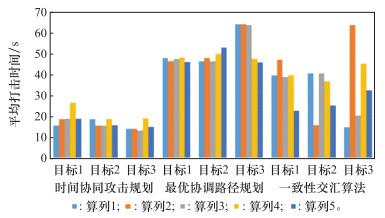
图 7的柱状图更为直观地表现了各目标在5种算例下的平均打击时间Timeave, 一致性交汇算法在不同算例中的表现波动较大, 而时间协同攻击规划算法和最右协调路径规划算法表现较为稳定,印证了将弹药航行纳入任务分配目标函数对协同打击目标任务的重要性。
图7
每个算例下3种算法的单目标打击时间差Timelagj如表 4所示。其中, 加粗的数值为每个算例下每个目标的最小打击时间差, 表格中的数值均为10次实验的平均值。在战场资源相对充足的情况下(如算例1~算例4), 单目标的打击时间差Timelagj均较为接近, 取得不错的打击效果。但在战场资源相对紧缺时, 最优协调路径规划和一致性交汇算法的打击时间出现较大的波动, 使得同时打击任务失效, 而时间协同攻击规划算法仍可以保持较低的打击时间差。由于时间协同攻击规划算法和最优协调路径规划算法都同时考虑到达航行的时间, 在战场资源不足的情况下, 相较于一致性交汇算法更为稳定, 有更佳的性能。由于最优协调路径规划算法中采用等长航迹的方法, 选择基准弹药航迹不同, 优先满足距离较远的个体, 导致在目标3的打击时间差优于时间协同攻击规划算法(如算例1~算例3), 整体性能时间协同攻击规划算法仍为最优。
表4 单目标打击时间差
Table 4
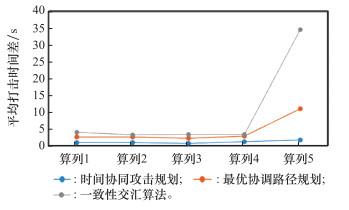
每个算例下3个目标的打击时间差的平均值如图 8所示。在各算例下, 时间协同攻击规划算法的打击时间差均为最小, 在战场资源相对紧缺(算例5)时, 该算法的稳定性更为明显。一致性交汇算法则表现最差, 在算例5中出现了较多目标的打击任务失败。最优协调路径规划算法的表现则介于两者之间。
图8
3.3.2 战场打击效能
在战场打击效能方面, 表 5以算例5为例, 展示了每个目标3种算法的战场打击效能W。在战场资源相对充足的情况下(如算例1~算例4), 各算法的打击效能W均较为接近, 可以取得较好的战场打击效能。但在战场资源相对紧缺时, 一致性交汇算法的战场效能极具下降, 航迹难以调节, 使得同时打击任务失败, 而时间协同攻击规划算法仍可以达到较高的打击效能,最优协调路径规划算法依然介于两者之间。
表5 打击效能
Table 5
由上述数值实验可以得出: 时间协同攻击规划算法在平均打击时间上取得了极大的性能提升, 明显优于最优协调路径规划算法和一致性交汇算法。由于本算法采用控制航行速度和改变航迹长度的规划方法, 与仅采用单一等长路径或仅控制航行速度方法相比具有更好的打击实时性。且在战场资源较为紧张的场景时, 由于本算法采用双层优化的决策方法, 与将任务分配和航迹规划解耦的方法相比, 可以保证规划结果的性能最优。
4 结束语
本文研究了固定翼集群弹药协同打击地面群体目标问题, 提出的任务规划方法在保证同时打击时间约束的前提下, 为各弹药规划分配结果和飞行航迹, 并取得较好的作战效能。数值实验中, 同最优协调路径规划和一致性交汇算法在多种算例下进行对比, 结果表明在任务时效性方面, 本文所提出的时间协同攻击规划算法取得了较大的性能提升; 在战场资源较为紧缺的情况下, 所提算法维持了较好的时效性和作战打击效果, 且具有更好的鲁棒性。
所提算法主要解决了协同打击时效和同时打击的问题, 但路径规划单元仍值得优化, 如何满足极端条件下的同时到达问题为下一阶段的研究重点。
参考文献
舰载近防武器对无人机蜂群的拦截分析
[J].
Analysis of shipborne close-in defense weapon system intercepting UAV swarm
[J].
无人机集群打击海面目标指定时间协同控制方法
[J].
Cooperative control method of designated time for UAV swarm attacking sea target
[J].
无人机协同作战兰彻斯特方程设计与作战进程预测
[J].DOI:10.3969/j.issn.1671-637X.2018.12.009 [本文引用: 1]
Design of Lanchester equation and prediction of operational process for cooperative operation of UAVs
[J].DOI:10.3969/j.issn.1671-637X.2018.12.009 [本文引用: 1]
UAVs task and motion planning in the presence of obstacles and prioritized targets
[J].DOI:10.3390/s151129734 [本文引用: 1]
Resource welfare based task allocation for UAV team with resource constraints
[J].
Online trajectory generation with rendezvous for UAVs using multistage path prediction
[J].DOI:10.1061/(ASCE)AS.1943-5525.0000694 [本文引用: 1]
Rendezvous of multiple UAVs with collision avoidance using consensus
[J].DOI:10.1061/(ASCE)AS.1943-5525.0000145 [本文引用: 5]
Multiple UAV coalitions for a search and prosecute mission
[J].
Cooperative path planning of multiple UAVs using Dubins paths with clothoid arcs
[J].DOI:10.1016/j.conengprac.2009.02.010 [本文引用: 1]
Multi-objective cooperative salvo attack against group target
[J].
考虑同时攻击约束的多异构无人机实时任务分配
[J].
Real-time task allocation for a heterogeneous multi-UAV simultaneous attack
[J].
Coordination variables, coordination functions, and cooperative timing missions
[J].
Coordinated target assignment and intercept for unmanned air vehicles
[J].
Assigning micro UAVs to task tours in an urban terrain
[J].
多无人机同时到达的分散化控制方法
[J].
Decentralized control for simultaneous arrival of multiple UAVs
[J].
An improved genetic algorithm with co-evolutionary strategy for global path planning of multiple mobile robots
[J].