0 引言
针对这一问题, 交互式多模型(interacting multiple model, IMM)[6-8]展现出更加优越的性能。近些年, IMM算法得到了很多学者的关注, 很多学者在结构和参数等层面对IMM算法进行了改进。文献[9]基于恒速和当前统计模型设计了IMM算法, 首先利用最小二乘法估计当前统计模型的平均速度, 然后将当前统计模型应用于IMM算法。该方法提高了模型精度, 从而提高了滤波精度。文献[10]从多个方面对IMM算法进行了改进, 包括采用改进的卡尔曼滤波器作为子滤波器、不同模型之间的非对称状态估计和基于熵的模型概率更新公式。文献[7, 11]提出了IMM的一种替代方法, 模型集中的模型由匀加速模型构成, 降低了模型集的复杂程度。在此基础上, 文献[12]提出了一种自适应IMM算法, 首先利用滤波器对目标的加速度进行估计, 然后选取估计加速度附近的值构建模型。该方法可以减少模型集中模型的数量, 在降低计算量的同时提高了模型精度。文献[13]基于二阶马尔可夫链提出了一种二阶IMM算法, 该算法利用了更多的先验信息, 提高了滤波精度。由于上述IMM模型集中的模型种类和数量不变, 所以又称其为固定结构IMM(fixed structure IMM, FSIMM)。
为了避免因模型不匹配而造成的精度误差问题, 在使用IMM算法时, 应使用尽可能多的模型覆盖目标机动模型。但值得注意的是, 单个模型集中模型过多, 同样会降低滤波精度[14]。在此背景下, 变结构IMM(variable structure IMM, VSIMM)应运而生。VSIMM经过不断的发展和改进, 大致可以分为4类: 模型组切换(model group switching, MGS)、可能模型集(likely mode set, LMS)、期望模型增强(expected mode augmentation, EMA)和自适应网格(adaptive grid, AG)[15]。其中, MGS将模型集分为模型子集, 一个时间步长只选择一个模型子集进行估计, 模型子集之间根据模型子集转移概率进行切换[16]。LMS将模型分为3种类型: 不可能的、重要的和主要的模型, 在每个时间步长里, 用于估计的模型子集由主要的模型和接近主要的模型构成[17-18]。与MGS类似, EMA将一个大的模型集分成小的模型子集, 然后计算下一个时间步长所有模型子集的概率, 选择概率最大的模型子集用于估计[19]。AG算法结合图理论, 将所有的模型构成一个网格, 利用先验信息和当前数据得到一个局部细化网格, 细化网格中的模型构成候选模型子集, 然后根据规则选择模型, 构成下一时刻用于滤波的模型子集[20]。
值得注意的是, 文献[19]所提到的EMA方法在计算似然函数和模型子集概率时, 对公式进行了近似。针对这一问题, 本文首先设计了一种新的VSIMM(novel VSIMM, NVSIMM)滤波算法, 给出了精确的数学模型。另外, 在前向NVSIMM滤波的基础上, 对数据进行平滑处理, 设计了VSIMM平滑(VSIMM smoothing, VSIMMS)算法, 前向NVSIMM和后向VSIMMS相结合即为VSIMM滤波和平滑(VSIMM filtering and smoothing, VSIMMFS)算法。
本文安排如下: 第1节对滤波和平滑问题进行了描述, 并给出了IMM滤波算法和IMM平滑算法的数学模型; 第2节设计了VSIMMFS算法, 包括前向NVSIMM滤波和后向VSIMM平滑两个部分; 第3节对本文所提算法的有效性进行仿真验证和讨论; 最后, 第4节给出了本文的结论。
1 IMM滤波和平滑算法
1.1 问题描述
假设目标可能有r个运动模型, 模型集记为Ω={M1, M2, …, Mr}, 模型之间的转换概率矩阵为
式中: pij(1≤i≤r, 1≤j≤r)为模型i到模型j的转移概率。
系统离散化状态方程如下:
式中: xkj为系统的状态向量; Fj为模型j的状态转移矩阵; wk-1j是均值为0的高斯白噪声, 其协方差矩阵为Qk-1j。
模型j的量测方程为
式中: zk为量测向量; Hj为模型j的测量矩阵; vkj是均值为0的高斯白噪声, 其协方差矩阵为Rkj。
基于上述状态方程、量测方程和贝叶斯理论, IMM滤波算法通过利用量测集合Zk={z1, z2, …, zk}和模型集Ω估计系统在k时刻的状态xk。而平滑的目的是根据当前所有的观测值Zk={z1, z2, …, zk}, 估计t时刻的系统状态
1.2 前向IMM滤波
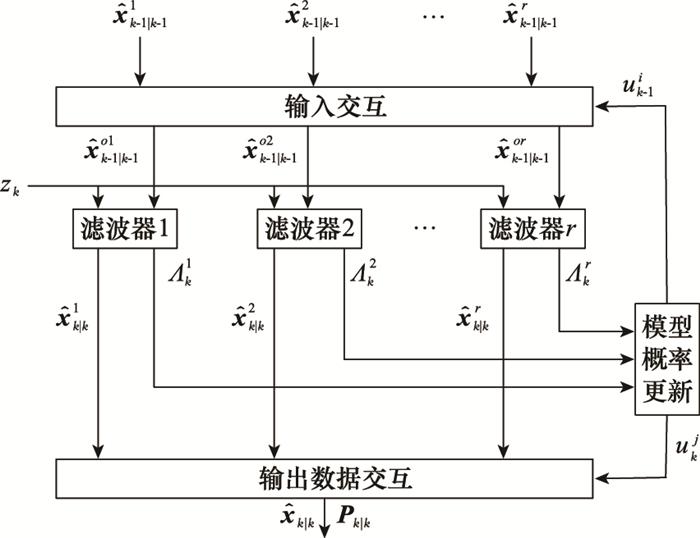
IMM算法框图如图 1所示。
图1
步骤1 前向输入交互
式中:
式中: uk-1i为模型i的概率, 预测概率
步骤2 滤波
分别基于每一个模型进行卡尔曼滤波:
步骤2.1 预测状态
步骤2.2 预测协方差矩阵
步骤2.3 计算卡尔曼增益
步骤2.4 滤波估计
步骤2.5 滤波值的协方差
步骤3 模型概率更新
模型概率更新公式为
式中: 分母p(zk|Zk-1)为归一化因子, 对分子积分即可得到, p{Mkj|Zk-1}=ckj在步骤1中已经求出, p{zk|Mkj, Zk-1}服从高斯分布, 其具体形式为
式中:
式中:
步骤4 输出
IMM滤波的状态估计和协方差估计分别为
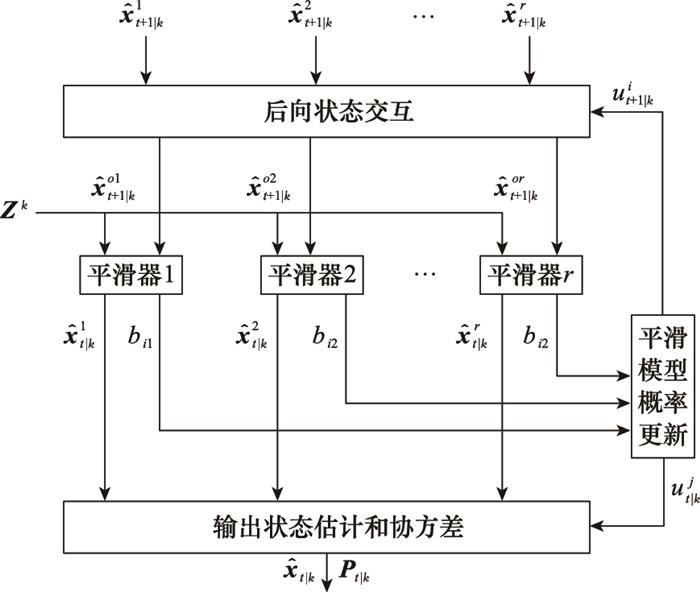
1.3 后向IMM平滑
图2
步骤1 后向状态交互
后向混合状态和对应的协方差为
式中: t+1=k时刻
式中:
式中:
步骤2 卡尔曼平滑[22]
平滑值和对应的协方差为
式中:
步骤3 平滑模型概率更新
平滑后的模型概率计算公式为
步骤4 IMM平滑状态交互
后向IMM平滑的状态输出和对应的协方差为
2 VSIMMFS算法
VSIMMFS算法包括前向NVSIMM滤波和后向VSIMM平滑两个部分, 这两个部分分别在后续两个小节中展开。
2.1 VSIMM滤波
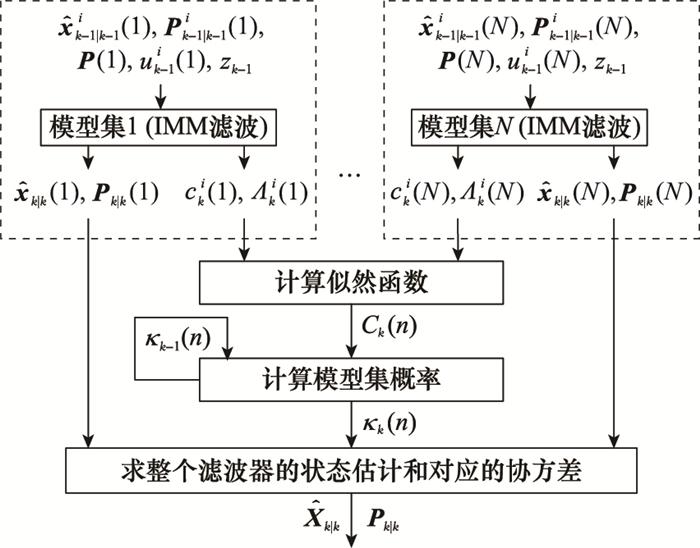
为了避免模型集中模型数量过多, 减少模型误差, 本节设计了NVSIMM算法。NVSIMM滤波算法包括多个模型子集, 每个模型子集独立运行IMM, 选取概率最高的模型子集的估计结果作为最终的估计状态输出。NVSIMM算法框图如图 3所示。
图3
算法包括以下4个步骤。
步骤1 并行独立IMM状态估计
针对不同的模型子集, 分别运行IMM算法得到状态估计值
步骤2 计算每个模型子集的似然函数
模型子集的似然函数为
式中: Πk(n)表示第n个模型子集, Λki(n)和cki(n)分别在步骤3和步骤1中求出。记p(zk|Zk-1, Πk(n))为Ck(n), 则有:
步骤3 计算模型子集概率
记模型子集概率p(Πk(m)|Zk)=κk(n), 则有:
式中: p(zk|Zk-1, Πk(n))在步骤2中已经求出, 分母为归一化因子, p(Πk(n)|Zk-1)根据全概率公式有:
式中: κk-1(m)=p(Πk-1(m)|Zk-1)为上一时刻的模型子集概率, 应用马尔可夫性质可知模型子集转移概率与观测值无关, 即:
步骤4 NVSIMM滤波状态估计
选择概率最大的模型子集的IMM估计结果作为最终的状态估计输出, 首先求出概率最高的模型子集编号:
从而可以得到最终的状态估计和对应的协方差为
2.2 VSIMMS算法
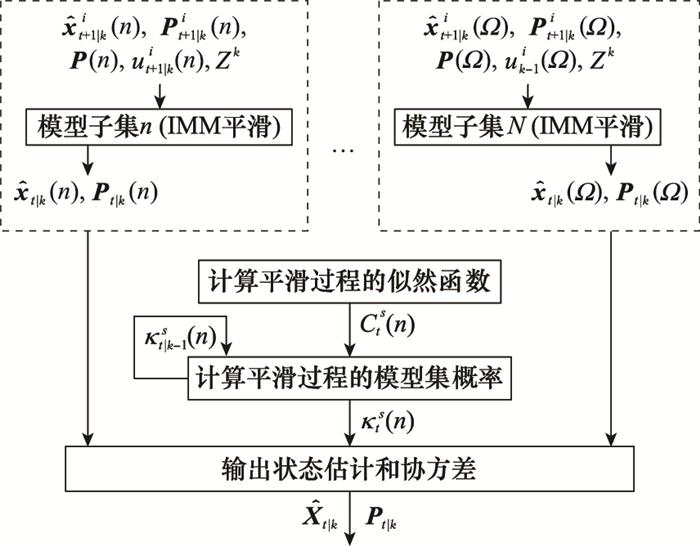
本节在NVSIMM的基础上, 对数据进行进一步平滑, 得到VSIMMS算法。VSIMMS算法框图如图 4所示。
图4
算法包括以下4个步骤。
步骤1 并行独立IMM状态平滑
针对不同的模型子集, 分别利用后向IMM平滑算法, 得到每个模型的平滑估计
步骤2 计算平滑后的模型子集的似然函数
应用全概率公式和马尔可夫性质, 可以得到模型子集的似然函数为
式中: p(zk|Zk-1, Πk(m))为前向NVSIMM滤波过程中模型子集的似然函数, 应用全概率公式和马尔可夫性质, p(Πk(m)|Πt(n))可以转化为
式中: p(Πt+1(nt+1)|Πt(n)), …, p(Πk(m)|Πk-1(nk-1))为模型子集转移概率, 在第2.1节步骤3中已经求出, 记模型子集转移概率
记
步骤3 计算平滑后的模型子集概率
根据贝叶斯定理可以得到模型子集概率为
式中: p(Πt(n)|Zk-1)在上一时刻的平滑过程中已经求出, 为已知值。p(zk|Zk-1, Πt(n))在步骤2中求出。记p(Πt(n)|Zk)=κt|ks(n), 式(38)可以变换为
步骤4 VSIMMS状态估计
概率最高的模型子集编号为
判断概率最高的模型子集在Tswitch时间段内是否发生变化。若发生变化, VSIMMS的状态估计和对应的协方差为
若不发生变化, VSIMMS的状态估计和对应的协方差为
3 仿真与讨论
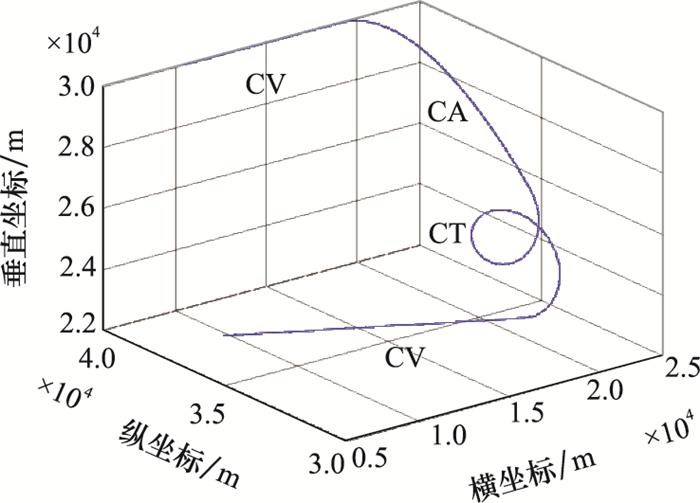
为了验证VSIMMFS算法的有效性, 本节首先针对三维空间中的目标运动轨迹展开分析讨论。目标的初始位置、速度和加速度分别为(10 km, 40 km, 30 km)、(300 m/s, 0, 0)和(0, 0, 0)。目标的机动参数如下:
(1) 30 s的匀速直线运动;
(2) 30 s的匀加速运动, 加速度大小为(-10 m/s2, -10 m/s2, -10 m/s2);
(3) 30 s的匀速转弯运动, 转弯角速率为(0.2 rad/s, 0.2 rad/s, 0);
(4) 30 s的匀速直线运动。
目标运动轨迹如图 5所示。
图5
利用蒙特卡罗法分析对比IMM、NVSIMM和VSIMMFS的性能, 其中IMM算法包括3个模型: 匀速直线运动(constant velocity, CV)模型、匀加速运动(constant acceleration, CA)模型和匀速转弯(constant turn, CT)模型[23-25]。VSIMMFS算法包括两个模型子集, 第一个模型子集包括CV、CA, 第二个模型子集包括CV、CT; NVSIMM滤波算法包括的模型子集和VSIMM相同。可以注意到, VSIMMFS和NVSIMM仅需两个原始模型子集即可包括所有的模型, 但这两种算法的原始模型子集并不包括模型子集CA、CT。设模型转移概率矩阵为
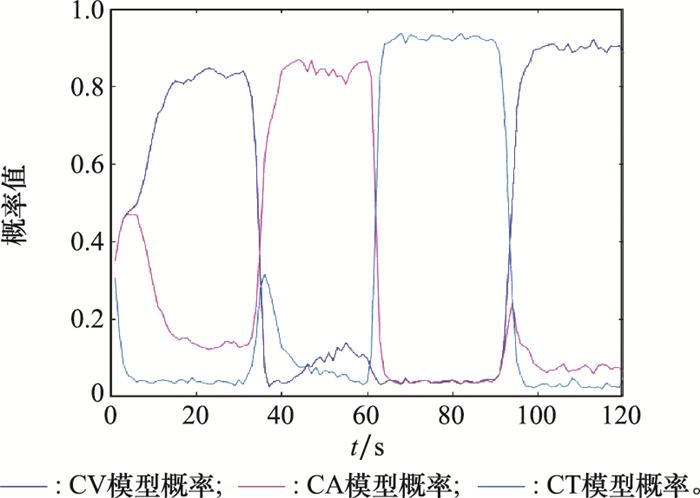
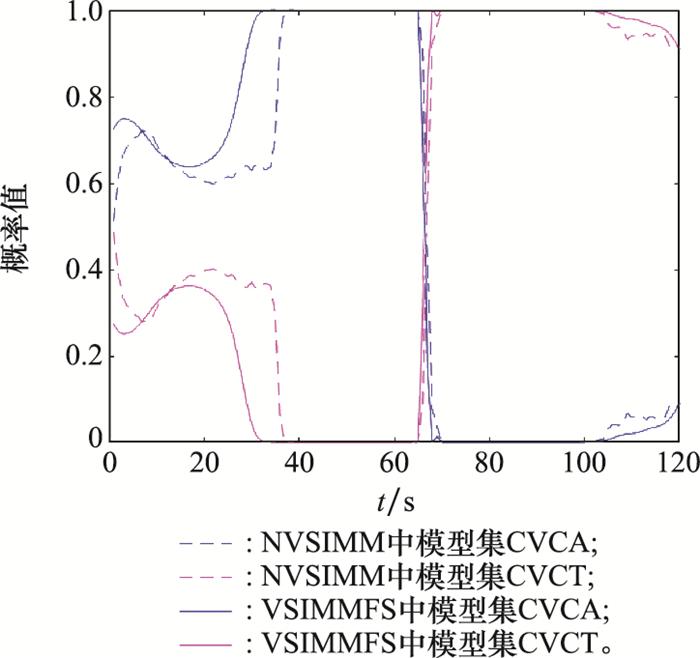
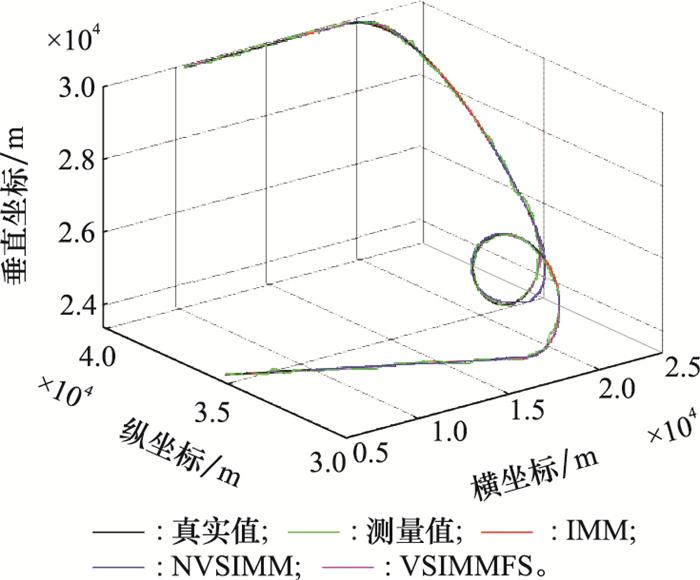
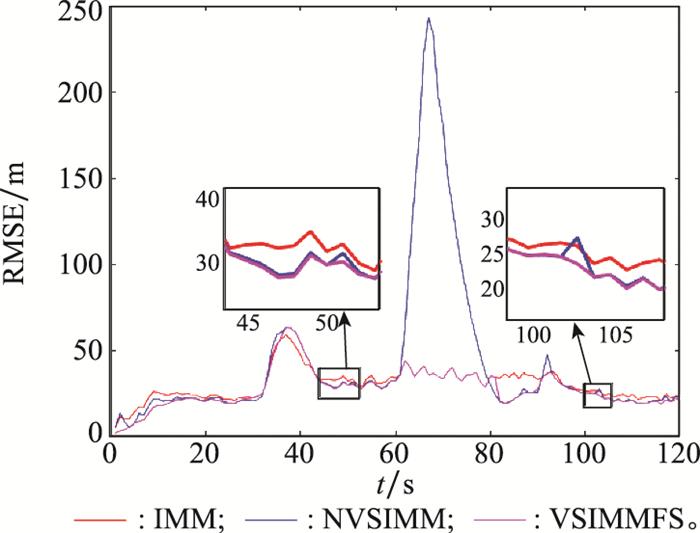
假设系统过程噪声的标准差为1 m/s2, 测量噪声的标准差为50 m, Tswitch=20 s, 仿真结果如图 6~图 9所示。图 6给出了IMM算法中模型概率变化曲线, 其中, 概率最大的曲线所对应的模型与目标实际机动模型相同。图 7给出了NVSIMM和VSIMMFS中模型子集概率曲线, 由图 7可知, 平滑后(VSIMMFS)的模型子集概率大于NVSIMM的模型子集概率, 说明平滑后的模型子集与目标机动模型匹配程度更高。另外, 对比图 6和图 7可知, 图 6中概率最大的曲线所对应的模型属于图 7中概率高的模型子集, 也就是说, 概率最高的模型子集始终包括目标实际的机动模型。图 8给出了IMM、NVSIMM和VSIMMFS对目标运动轨迹的跟踪效果, 这3种方法都能够对目标轨迹进行较好的估计, 三者之间的差异具体体现在图 9中。图 9给出了IMM、NVSIMM和VSIMMFS对目标位置估计的均方根误差(root mean square error, RMSE)曲线。从图 9中可以看出, VSIMMFS的RMSE最小, VSIMMFS次之, IMM的RMSE最大。值得注意的是, 概率最大的模型子集发生变化时, NVSIMM算法的性能会短暂下降, 而VSIMMFS算法对位置估计的RMSE与IMM相同, 原因在于在设计VSIMMFS算法时, 当最大概率的模型子集短暂发生时, 利用基于模型全集的IMM估计值作为VSIMMFS的估计值, 从而避免了VSIMMFS算法短暂的性能下降。
图6
图7
图7
NVSIMM和VSIMMFS中模型子集概率
Fig.7
Model subset probabilities in NVSIMM and VSIMMFS
图8
图9
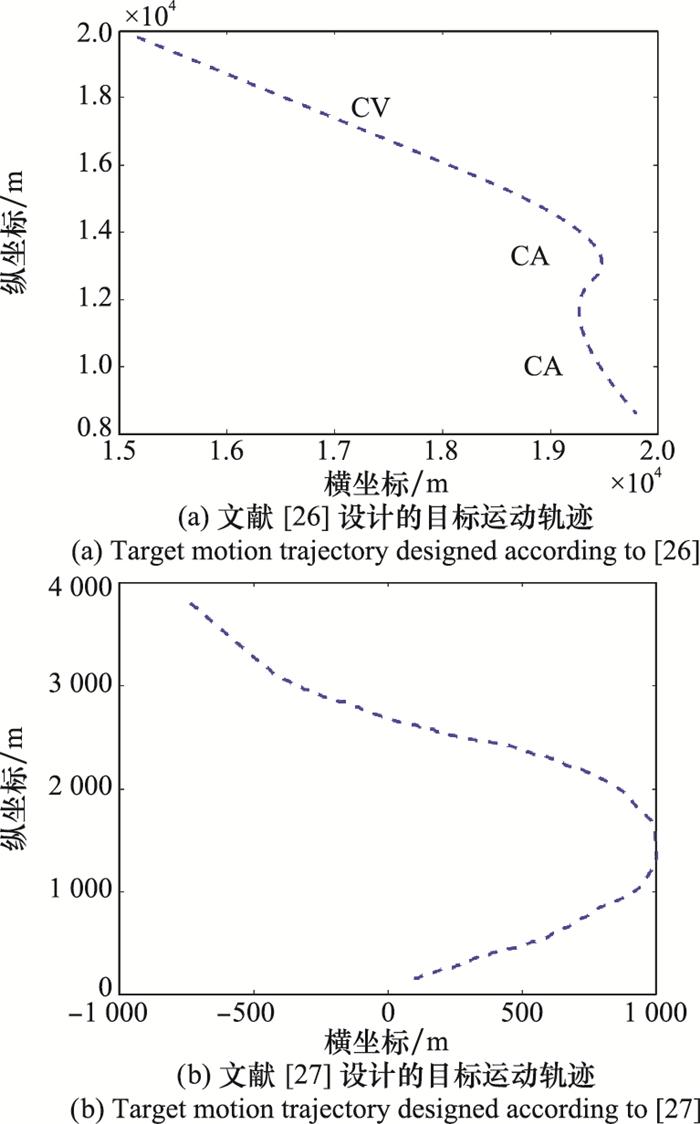
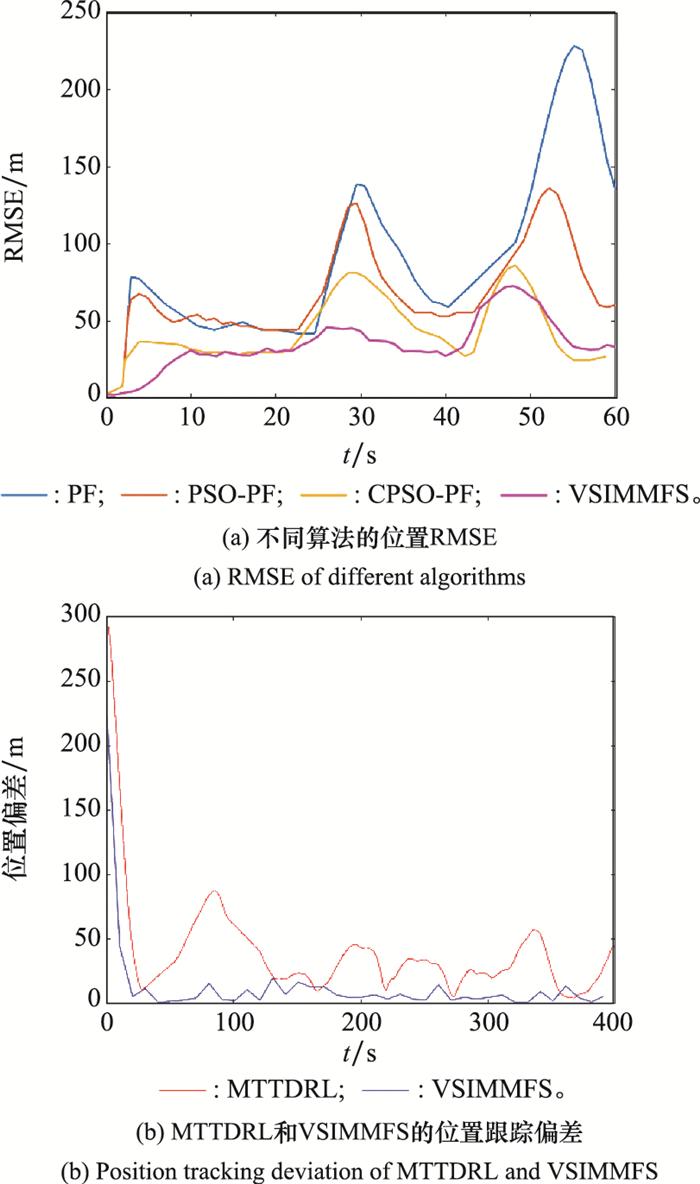
为了进一步体现VSIMMFS算法的优越性, 将VSIMMFS与基于深度强化学习的目标跟踪算法(maneuvering target tracking based on deep reinforcement learning, MTTDRL)[27]、粒子滤波(particle filter, PF)[28]、基于粒子群优化的PF(particle swarm optimization algorithm-based PF, PSO-PF)[29]、基于混沌PSO-PF(chaos PSO-PF, CPSO-PF)[26, 30]进行对比。为了保证对比的有效性, 仿真参数参考文献[26]和文献[27]设计, 目标的运动轨迹如图 10所示。图 11分析对比了上述算法对目标位置的跟踪性能。由图 11(a)可知, 相比于PF、PSO-PF和CPSO-PF, VSIMMFS的位置跟踪的RMSE较小; 从图 11(b)可以看出, 利用VSIMMFS对目标跟踪时的位置偏差更小。所以综上可知, VSIMMFS的跟踪性能优于上述其他算法。
图10
图11
4 结论
为了进一步提高对机动目标的跟踪精度, 本文设计了一种VSIMMFS算法。该方法包括前向VSIMM滤波和后向VSIMMS两个部分, 通过并行独立运行IMM滤波和IMM平滑, 选择概率最大的模型子集的估计结果作为最终的状态估计值。通过与IMM、NVSIMM、PF、PSO-PF、CPSO-PF和MTTDRL算法比较, VSIMMFS具有更好的跟踪性能。
参考文献
A novel adaptive state of charge estimation method of full life cycling lithium-ion batteries based on the multiple parameter optimization
[J].
A novel safety assurance method based on the compound equivalent modeling and iterate reduce particle-adaptive Kalman filtering for the unmanned aerial vehicle lithium ion batteries
[J].
A critical review of improved deep learning methods for the remaining useful life prediction of lithium-ion batteries
[J].DOI:10.1016/j.egyr.2021.08.182
Spatial-temporal constrained particle filter for cooperative target tracking
[J].DOI:10.1016/j.jnca.2020.102913 [本文引用: 1]
The interacting multiple model algorithm for systems with Markovian switching coefficients
[J].
An interacting multiple model for trajectory prediction of intelligent vehicles in typical road traffic scenario
[J].DOI:10.1109/TNNLS.2021.3136866 [本文引用: 1]
IMM estimator based on fuzzy weighted input estimation for tracking a maneuvering target
[J].DOI:10.1016/j.apm.2015.02.031 [本文引用: 1]
Interacting multiple model filter for tactical ballistic missile tracking
[J].DOI:10.1109/TAES.2008.4560196 [本文引用: 1]
Radar target tracking-Viterbi versus IMM
[J].
Adaptive interacting multiple model algorithm for tracking a manoeuvring target
[J].DOI:10.1049/ip-rsn:19951528 [本文引用: 1]
Second-order Markov chain based multiple-model algorithm for maneuvering target tracking
[J].DOI:10.1109/TAES.2013.6404088 [本文引用: 1]
The new trend of state estimation: from model-driven to hybrid-driven methods
[J].DOI:10.3390/s21062085 [本文引用: 1]
Remaining useful life estimation of Lithium-ion battery based on interacting multiple model particle filter and support vector regression
[J].
Multiple-model estimation with variable structure. V. Likely-model set algorithm
[J].DOI:10.1109/7.845222 [本文引用: 1]
Extending the unified theory of acceptance and use of technology to investigate determinants of acceptance and adoption of learning management systems in the post-pandemic era: a structural equation modeling approach
[J].
A novel interacting multiple model algorithm
[J].DOI:10.1016/j.sigpro.2009.04.033 [本文引用: 2]
Tracking of maneuver-ing extended target using modified variable structure multiple-model based on adaptive grid best model augmentation
[J].DOI:10.3390/rs14071613 [本文引用: 1]
Adaptive dynamic state estimation of distribution network based on interacting multiple model
[J].
Stacked LSTM based deep recurrent neural network with Kalman smoothing for blood glucose prediction
[J].DOI:10.1186/s12911-021-01462-5 [本文引用: 1]
Survey of maneuvering target tracking. Part Ⅰ: dynamic models
[J].DOI:10.1109/TAES.2003.1261132 [本文引用: 1]
Hummingbirds optimization algorithm-based particle filter for maneuvering target tracking
[J].DOI:10.1007/s11071-019-05043-0 [本文引用: 2]
UAV maneuvering target tracking based on deep reinforcement learning
[J].DOI:10.1088/1742-6596/1958/1/012015 [本文引用: 2]
A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking
[J].DOI:10.1109/78.978374 [本文引用: 1]
Particle filter based on particle swarm optimization resampling for vision tracking
[J].DOI:10.1016/j.eswa.2010.05.086 [本文引用: 1]
Fault detection and isolation in GPS receiver autonomous integrity monitoring based on chaos particle swarm optimization-particle filter algorithm
[J].DOI:10.1016/j.asr.2017.12.016 [本文引用: 1]