图1
LSTM网络结构图
Fig.1
Architecture of LSTM network
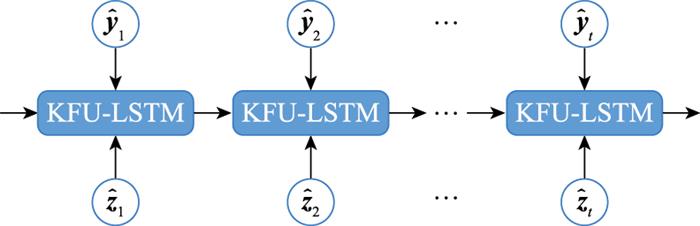
图2
KFU-LSTM-Net结构图
Fig.2
Structure of KFU-LSTM-Net
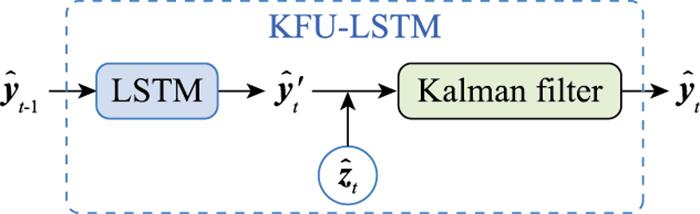
图3
KFU-LSTM模块内部结构图
Fig.3
Internal structure of KFU-LSTM block
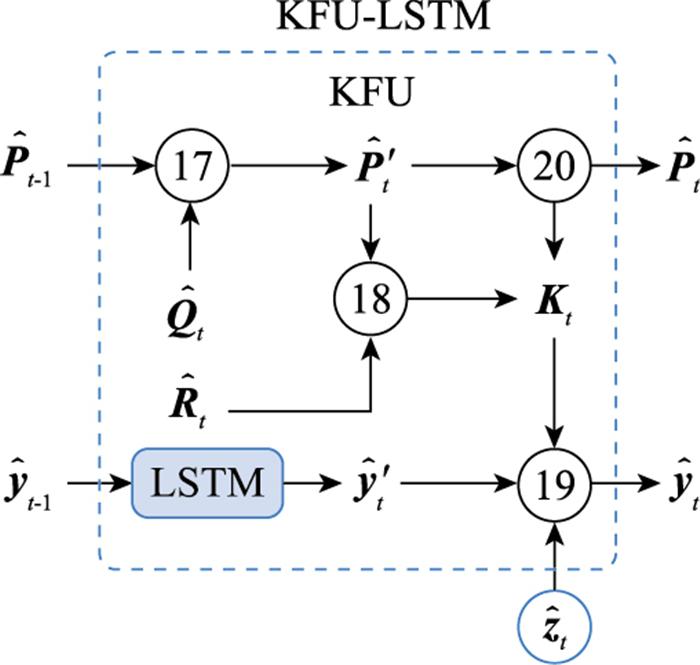
图4
卡尔曼滤波算法展开图
Fig.4
Kalman filter algorithm unfolding diagram
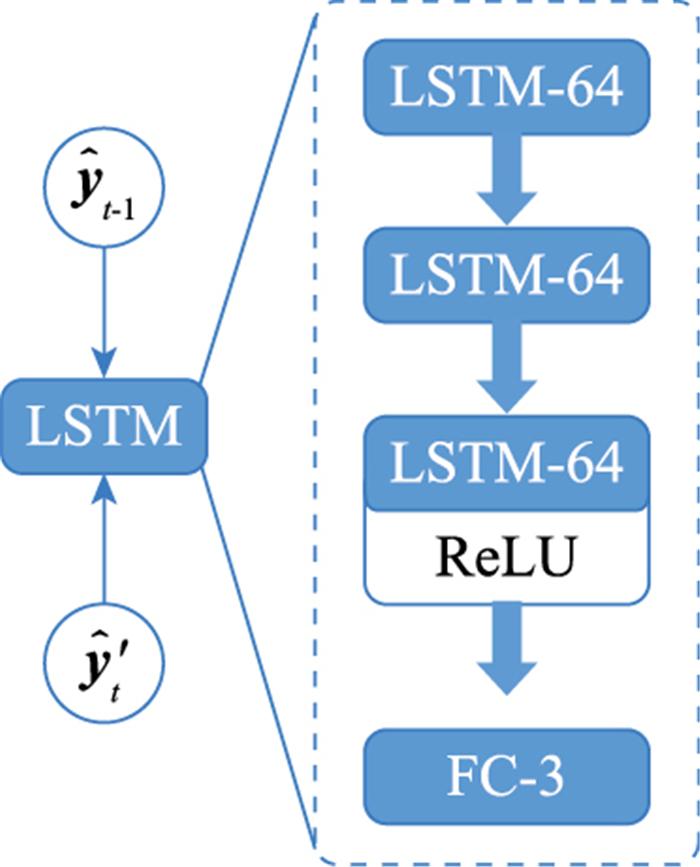
图5
LSTM模块结构图
Fig.5
LSTM block structure
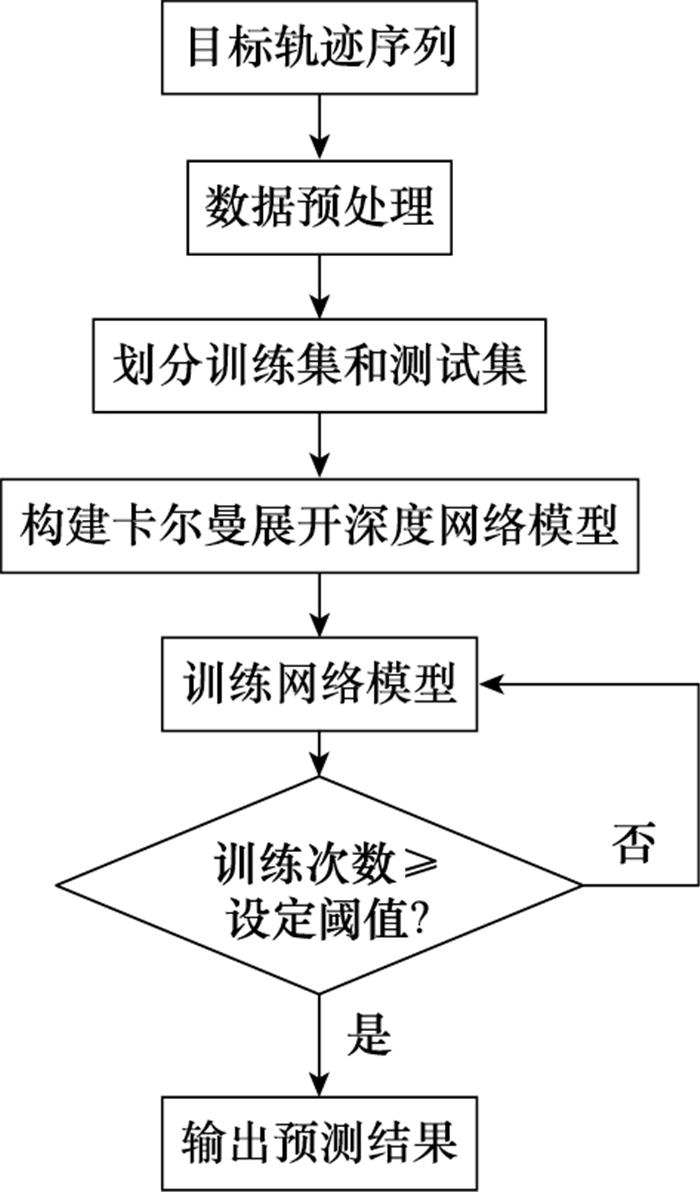
图6
模型整体预测流程图
Fig.6
Overall prediction flowchart of the model
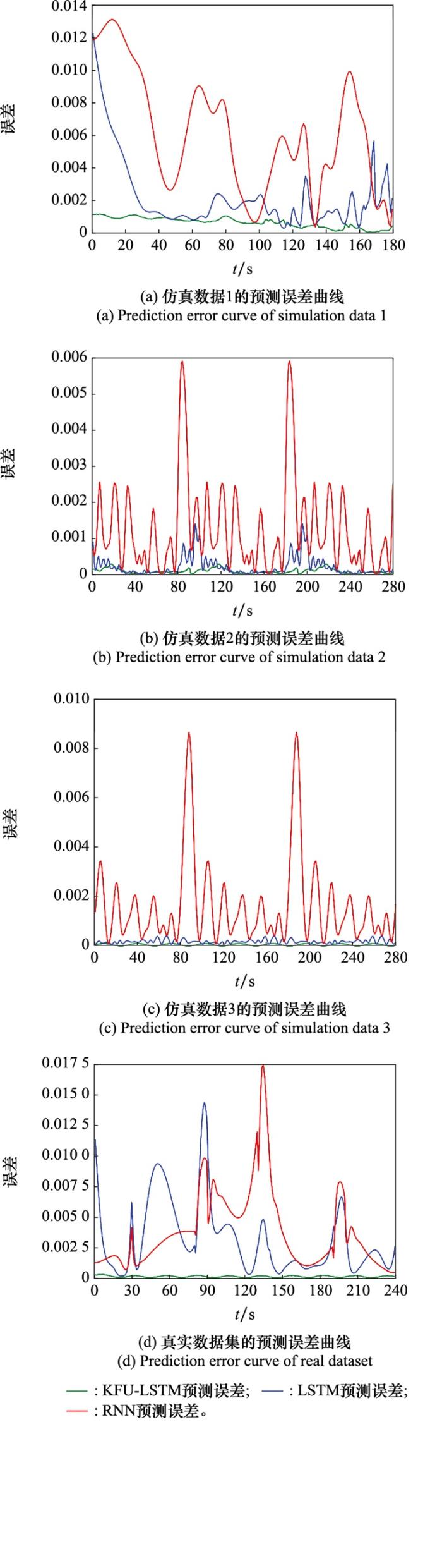
图7
模型轨迹预测误差对比图
Fig.7
Comparison of model track prediction errors
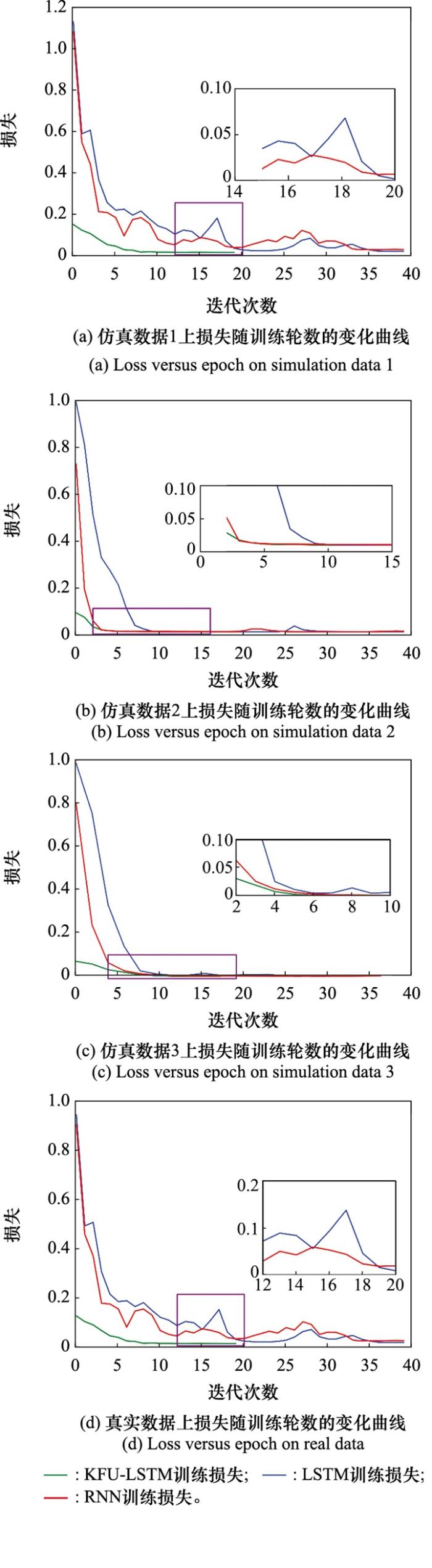
图8
模型损失随训练轮数变化对比图
Fig.8
Comparison diagram of model loss with epochs
[28]
BENGIO Y , SIMARD P , FRASCONI P . Learning long-term dependencies with gradient descent is difficult
[J]. IEEE Trans.on Neural Networks , 1994 , 5 (2 ): 157 - 166 .
URL
[本文引用: 1]
[29]
GREFF K , SRIVASTAVA R K , KOUTNIK J , et al . LSTM: a search space odyssey
[J]. IEEE Trans.on Neural Networks and Learning Systems , 2016 , 28 (10 ): 2222 - 2232 .
URL
[本文引用: 1]
[30]
SHERSTINSKY A . Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network
[J]. Physica D: Nonlinear Phenomena , 2020 , 404 , 132306 .
URL
[本文引用: 1]
[31]
GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[C]//Proc. of the 13th International Conference on Artificial Intelligence and Statistics, 2010.
[本文引用: 1]
[32]
KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. [2022-01-07]. https://arxiv.org/abs/1412.6980 .
[本文引用: 1]
[1]
ZENG W L , CHU X , XU Z F , et al . Aircraft 4D trajectory prediction in civil aviation: a review
[J]. Aerospace , 2022 , 9 (2 ): 91 - 109 .
DOI:10.3390/aerospace9020091
[本文引用: 1]
[2]
LIU R W , LIANG M H , NIE J T , et al . Deep learning-powered vessel trajectory prediction for improving smart traffic services in maritime Internet of Things
[J]. IEEE Trans.on Network Science and Engineering , 2022 , 9 (5 ): 3080 - 3094 .
DOI:10.1109/TNSE.2022.3140529
[3]
LEON F , GAVRILESCU M . A review of tracking and trajectory prediction methods for autonomous driving
[J]. Mathematics , 2021 , 9 (6 ): 660 - 696 .
DOI:10.3390/math9060660
[本文引用: 1]
[4]
LYMPEROPOULOS I, LYGEROS J, LECCHINI A. Model based aircraft trajectory prediction during takeoff[C]//Proc. of the AIAA Guidance, Navigation, and Control Conference and Exhibit, 2006.
[本文引用: 1]
[5]
GALLO E. Quasi static atmospheric model for aircraft trajectory prediction and flight simulation[EB/OL]. [2022-01-07]. https://arxi.org/abs/2101.10744 .
[6]
JIANG S Y , LUO X , HE L . Research on method of trajectory prediction in aircraft flight based on aircraft performance and historical track data
[J]. Mathematical Problems in Engineering , 2021 , 2021 , 6688213 .
[7]
SCHULTZ C, THIPPHAVONG D, ERZBERGER H. Adaptive trajectory prediction algorithm for climbing flights[C]//Proc. of the AIAA Guidance, Navigation, and Control Conference, 2012.
[8]
SCHUSTER W , PORRETTA M , OCHIENG W . High-accuracy four-dimensional trajectory prediction for civil aircraft
[J]. The Aeronautical Journal , 2012 , 116 (1175 ): 45 - 66 .
DOI:10.1017/S0001924000006618
[9]
BENAVIDES J V, KANESHIGE J, SHARMA S, et al. Implementation of a trajectory prediction function for trajectory based operations[C]//Proc. of the AIAA Atmospheric Flight Mechanics Conference, 2014.
[本文引用: 1]
[10]
LIU W , LIANG X , ZHENG M . Dynamic model informed human motion prediction based on unscented kalman filter
[J]. IEEE/ASME Trans.on Mechatronics , 2022 , 27 (6 ): 5287 - 5295 .
DOI:10.1109/TMECH.2022.3173167
[本文引用: 1]
[11]
JULIER S J, UHLMANN J K. New extension of the Kalman filter to nonlinear systems[C]//Proc. of the Signal Processing, Sensor Fusion, and Target Recognition VI. International Society for Optics and Photonics, 1997.
[本文引用: 1]
[12]
GUO G , ZHAO S J . 3D multi-object tracking with adaptive cubature Kalman filter for autonomous driving
[J]. IEEE Trans.on Intelligent Vehicles , 2023 , 8 (1 ): 512 - 519 .
DOI:10.1109/TIV.2022.3158419
[13]
QIAO S J , HAN N , ZHU X W , et al . A dynamic trajectory prediction algorithm based on Kalman filter
[J]. Acta Electonica Sinica , 2018 , 46 (2 ): 418 - 423 .
[本文引用: 1]
[14]
CHOI H C , DENG C , HWANG I . Hybrid machine learning and estimation-based flight trajectory prediction in terminal airspace
[J]. IEEE Access , 2021 , 9 , 151186 - 151197 .
DOI:10.1109/ACCESS.2021.3126117
[本文引用: 1]
[15]
HASHEMI S M , BOTEZ R M , GRIGORIE T L . New reliabi-lity studies of data-driven aircraft trajectory prediction
[J]. Aerospace , 2020 , 7 (10 ): 145 - 152 .
DOI:10.3390/aerospace7100145
[16]
SCHIMPF N, KNOBLOCK E J, WANG Z, et al. Flight tra-jectory prediction based on hybrid-recurrent networks[C]// Proc. of the IEEE Cognitive Communications for Aerospace Applications Workshop, 2021.
[本文引用: 1]
[17]
PANG Y T, LIU Y M. Conditional generative adversarial networks (CGAN) for aircraft trajectory prediction considering weather effects[C]//Proc. of the AIAA Scitech Forum, 2020.
[本文引用: 1]
[18]
DALMAU R , PRATS X , VERHOEVEN R , et al . Comparison of various guidance strategies to achieve time constraints in optimal descents
[J]. Journal of Guidance, Control, and Dynamics , 2019 , 42 (7 ): 1612 - 1621 .
DOI:10.2514/1.G004019
[本文引用: 1]
[19]
吕波 , 王超 . 改进的扩展卡尔曼滤波在航空器4D航迹预测算法中的应用
[J]. 计算机应用 , 2021 , 41 (S1 ): 277 - 282 .
URL
[本文引用: 1]
LYU B , WANG C . Application of improved extended Kalman filter in 4D flight path prediction algorithm of aircraft
[J]. Journal of Computer Applications , 2021 , 41 (S1 ): 277 - 282 .
URL
[本文引用: 1]
[21]
ZHANG X W, YU W Z. Research on the application of Kalman filter algorithm in aircraft trajectory analysis[C]//Proc. of the IEEE 7th International Conference on Intelligent Computing and Signal Processing, 2022.
[本文引用: 1]
[22]
RALAIVOLA L, D'ALCHE-BUC F. Time series filtering, smoothing and learning using the kernel Kalman filter[C]// Proc. of the IEEE International Joint Conference on Neural Networks, 2005.
[本文引用: 1]
[23]
钱夔 , 周颖 , 杨柳静 , 等 . 基于BP神经网络的空中目标航迹预测模型
[J]. 指挥信息系统与技术 , 2017 , 8 (3 ): 54 - 58 .
URL
[本文引用: 1]
QIAN K , ZHOU Y , YANG L J , et al . Air target track prediction model based on BP neural network
[J]. Command Information System and Technology , 2017 , 8 (3 ): 54 - 58 .
URL
[本文引用: 1]
[25]
GRAVES A, MOHAMED A, HINTON G. Speech recognition with deep recurrent neural networks[C]//Proc. of the IEEE International Conference on Acoustics, Speech and Signal Processing, 2013.
[本文引用: 1]
[27]
HOCHREITER S . Recurrent neural net learning and vanishing gradient
[J]. International Journal of Uncertainity, Fuzziness and Knowledge-Based Systems , 1998 , 6 (2 ): 107 - 116 .
DOI:10.1142/S0218488598000094
[本文引用: 2]
Learning long-term dependencies with gradient descent is difficult
1
1994
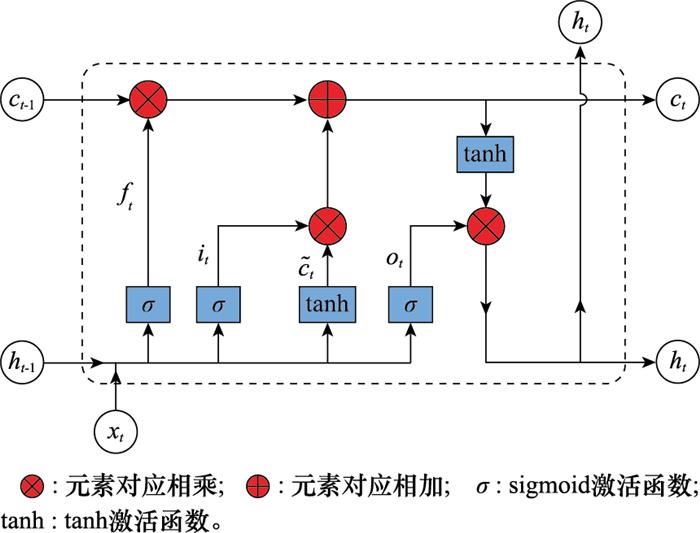
... LSTM神经网络是专门为解决长时间序列难以记忆[28 ] 和梯度消失的问题而引入的,并已成为最广泛使用的网络架构之一.LSTM网络的隐藏层中包含了遗忘门、输入门、输出门,它们不仅控制着信息的流动模式,而且对网络预测的性能而言至关重要[29 -30 ] .LSTM神经元内部的计算公式如下: ...
LSTM: a search space odyssey
1
2016
... LSTM神经网络是专门为解决长时间序列难以记忆[28 ] 和梯度消失的问题而引入的,并已成为最广泛使用的网络架构之一.LSTM网络的隐藏层中包含了遗忘门、输入门、输出门,它们不仅控制着信息的流动模式,而且对网络预测的性能而言至关重要[29 -30 ] .LSTM神经元内部的计算公式如下: ...
Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network
1
2020
... LSTM神经网络是专门为解决长时间序列难以记忆[28 ] 和梯度消失的问题而引入的,并已成为最广泛使用的网络架构之一.LSTM网络的隐藏层中包含了遗忘门、输入门、输出门,它们不仅控制着信息的流动模式,而且对网络预测的性能而言至关重要[29 -30 ] .LSTM神经元内部的计算公式如下: ...
1
... (3) 训练策略:本文网络中,所有的权重矩阵用Xavier进行随机初始化[31 ] ,偏差均初始化为0,目标初始状态估计值为目标起始点y 0 ,初始状态协方差矩阵$ \hat{\boldsymbol{P}}'_{0}$ I [32 ] ,设定训练批尺寸为16.网络模型的训练策略及参数设定如表 1 所示.网络模型在数据集上进行训练,从而通过梯度反传自适应地学习网络各参数.本文所有实验均在Windows10(64 bit)操作系统的Pytorch平台中运行,电脑设备硬件配置为Intel Core i7-9750H CPU和NVIDIA GTX 1660Ti.实验环境如表 2 所示. ...
1
... (3) 训练策略:本文网络中,所有的权重矩阵用Xavier进行随机初始化[31 ] ,偏差均初始化为0,目标初始状态估计值为目标起始点y 0 ,初始状态协方差矩阵$ \hat{\boldsymbol{P}}'_{0}$ I [32 ] ,设定训练批尺寸为16.网络模型的训练策略及参数设定如表 1 所示.网络模型在数据集上进行训练,从而通过梯度反传自适应地学习网络各参数.本文所有实验均在Windows10(64 bit)操作系统的Pytorch平台中运行,电脑设备硬件配置为Intel Core i7-9750H CPU和NVIDIA GTX 1660Ti.实验环境如表 2 所示. ...
Aircraft 4D trajectory prediction in civil aviation: a review
1
2022
... 目标轨迹预测作为航空和军事领域的重点研究问题,一直受到学界和工业界的广泛关注[1 -3 ] .随着近现代信息科学技术的不断发展,目标轨迹预测的方法和模型也在不断更新和改进.目标轨迹预测即利用当前时刻目标的状态信息预测目标下一时刻的状态,该任务可等效地看作针对时间序列的预测问题.飞行目标轨迹预测模型分可为动力学模型[4 -9 ] 、卡尔曼滤波(Kalman filter, KF)算法模型[10 -13 ] 和机器学习模型[14 -16 ] . ...
Deep learning-powered vessel trajectory prediction for improving smart traffic services in maritime Internet of Things
0
2022
A review of tracking and trajectory prediction methods for autonomous driving
1
2021
... 目标轨迹预测作为航空和军事领域的重点研究问题,一直受到学界和工业界的广泛关注[1 -3 ] .随着近现代信息科学技术的不断发展,目标轨迹预测的方法和模型也在不断更新和改进.目标轨迹预测即利用当前时刻目标的状态信息预测目标下一时刻的状态,该任务可等效地看作针对时间序列的预测问题.飞行目标轨迹预测模型分可为动力学模型[4 -9 ] 、卡尔曼滤波(Kalman filter, KF)算法模型[10 -13 ] 和机器学习模型[14 -16 ] . ...
1
... 目标轨迹预测作为航空和军事领域的重点研究问题,一直受到学界和工业界的广泛关注[1 -3 ] .随着近现代信息科学技术的不断发展,目标轨迹预测的方法和模型也在不断更新和改进.目标轨迹预测即利用当前时刻目标的状态信息预测目标下一时刻的状态,该任务可等效地看作针对时间序列的预测问题.飞行目标轨迹预测模型分可为动力学模型[4 -9 ] 、卡尔曼滤波(Kalman filter, KF)算法模型[10 -13 ] 和机器学习模型[14 -16 ] . ...
Research on method of trajectory prediction in aircraft flight based on aircraft performance and historical track data
0
2021
High-accuracy four-dimensional trajectory prediction for civil aircraft
0
2012
1
... 目标轨迹预测作为航空和军事领域的重点研究问题,一直受到学界和工业界的广泛关注[1 -3 ] .随着近现代信息科学技术的不断发展,目标轨迹预测的方法和模型也在不断更新和改进.目标轨迹预测即利用当前时刻目标的状态信息预测目标下一时刻的状态,该任务可等效地看作针对时间序列的预测问题.飞行目标轨迹预测模型分可为动力学模型[4 -9 ] 、卡尔曼滤波(Kalman filter, KF)算法模型[10 -13 ] 和机器学习模型[14 -16 ] . ...
Dynamic model informed human motion prediction based on unscented kalman filter
1
2022
... 目标轨迹预测作为航空和军事领域的重点研究问题,一直受到学界和工业界的广泛关注[1 -3 ] .随着近现代信息科学技术的不断发展,目标轨迹预测的方法和模型也在不断更新和改进.目标轨迹预测即利用当前时刻目标的状态信息预测目标下一时刻的状态,该任务可等效地看作针对时间序列的预测问题.飞行目标轨迹预测模型分可为动力学模型[4 -9 ] 、卡尔曼滤波(Kalman filter, KF)算法模型[10 -13 ] 和机器学习模型[14 -16 ] . ...
1
... KF算法模型是一种应用非常广泛且有效的目标轨迹预测方法.Julier等[11 ] 在1997年提出了扩展KF(extend KF, EKF)算法,该算法不仅继承了KF算法的优势,而且能够处理非线性系统模型.吕波等[19 ] 利用EKF嵌入非线性控制系统,针对航空器的航迹预测任务建立了多信息EKF预测模型.陈明强等[20 ] 提出了基于无迹KF的航迹预测模型, 并完成了对飞行目标的航迹预测.然而,在现实的许多目标轨迹预测任务中,一般不能预先指定运动模型,在这种情况下,卡尔曼滤波器的应用受到了严重的限制[21 -22 ] .此外,KF算法通常是在恒定加速度的假设下应用的,这也是对现实目标运动情况的粗略逼近,这样建立的算法模型对目标轨迹预测的精度有限.为了克服传统KF算法的局限性,许多学者尝试直接从训练数据中学习运动模型.利用可学习模型来学习目标运动方程, 可以避免手工设计KF转移矩阵和测量矩阵,从而提高目标轨迹预测精度. ...
3D multi-object tracking with adaptive cubature Kalman filter for autonomous driving
0
2023
A dynamic trajectory prediction algorithm based on Kalman filter
1
2018
... 目标轨迹预测作为航空和军事领域的重点研究问题,一直受到学界和工业界的广泛关注[1 -3 ] .随着近现代信息科学技术的不断发展,目标轨迹预测的方法和模型也在不断更新和改进.目标轨迹预测即利用当前时刻目标的状态信息预测目标下一时刻的状态,该任务可等效地看作针对时间序列的预测问题.飞行目标轨迹预测模型分可为动力学模型[4 -9 ] 、卡尔曼滤波(Kalman filter, KF)算法模型[10 -13 ] 和机器学习模型[14 -16 ] . ...
Hybrid machine learning and estimation-based flight trajectory prediction in terminal airspace
1
2021
... 目标轨迹预测作为航空和军事领域的重点研究问题,一直受到学界和工业界的广泛关注[1 -3 ] .随着近现代信息科学技术的不断发展,目标轨迹预测的方法和模型也在不断更新和改进.目标轨迹预测即利用当前时刻目标的状态信息预测目标下一时刻的状态,该任务可等效地看作针对时间序列的预测问题.飞行目标轨迹预测模型分可为动力学模型[4 -9 ] 、卡尔曼滤波(Kalman filter, KF)算法模型[10 -13 ] 和机器学习模型[14 -16 ] . ...
New reliabi-lity studies of data-driven aircraft trajectory prediction
0
2020
1
... 目标轨迹预测作为航空和军事领域的重点研究问题,一直受到学界和工业界的广泛关注[1 -3 ] .随着近现代信息科学技术的不断发展,目标轨迹预测的方法和模型也在不断更新和改进.目标轨迹预测即利用当前时刻目标的状态信息预测目标下一时刻的状态,该任务可等效地看作针对时间序列的预测问题.飞行目标轨迹预测模型分可为动力学模型[4 -9 ] 、卡尔曼滤波(Kalman filter, KF)算法模型[10 -13 ] 和机器学习模型[14 -16 ] . ...
1
... 动力学模型根据目标运动的空气动力学方程,对目标的轨迹进行预测,但在现实中,飞行目标往往受到天气、环境等诸多因素的影响[17 ] ,而且目标飞行过程的受力复杂多变,根据空气动力学建立的目标运动模型对实际情况进行了较大程度的简化,由此导致这类模型对目标轨迹预测的精度较低[18 ] . ...
Comparison of various guidance strategies to achieve time constraints in optimal descents
1
2019
... 动力学模型根据目标运动的空气动力学方程,对目标的轨迹进行预测,但在现实中,飞行目标往往受到天气、环境等诸多因素的影响[17 ] ,而且目标飞行过程的受力复杂多变,根据空气动力学建立的目标运动模型对实际情况进行了较大程度的简化,由此导致这类模型对目标轨迹预测的精度较低[18 ] . ...
改进的扩展卡尔曼滤波在航空器4D航迹预测算法中的应用
1
2021
... KF算法模型是一种应用非常广泛且有效的目标轨迹预测方法.Julier等[11 ] 在1997年提出了扩展KF(extend KF, EKF)算法,该算法不仅继承了KF算法的优势,而且能够处理非线性系统模型.吕波等[19 ] 利用EKF嵌入非线性控制系统,针对航空器的航迹预测任务建立了多信息EKF预测模型.陈明强等[20 ] 提出了基于无迹KF的航迹预测模型, 并完成了对飞行目标的航迹预测.然而,在现实的许多目标轨迹预测任务中,一般不能预先指定运动模型,在这种情况下,卡尔曼滤波器的应用受到了严重的限制[21 -22 ] .此外,KF算法通常是在恒定加速度的假设下应用的,这也是对现实目标运动情况的粗略逼近,这样建立的算法模型对目标轨迹预测的精度有限.为了克服传统KF算法的局限性,许多学者尝试直接从训练数据中学习运动模型.利用可学习模型来学习目标运动方程, 可以避免手工设计KF转移矩阵和测量矩阵,从而提高目标轨迹预测精度. ...
Application of improved extended Kalman filter in 4D flight path prediction algorithm of aircraft
1
2021
... KF算法模型是一种应用非常广泛且有效的目标轨迹预测方法.Julier等[11 ] 在1997年提出了扩展KF(extend KF, EKF)算法,该算法不仅继承了KF算法的优势,而且能够处理非线性系统模型.吕波等[19 ] 利用EKF嵌入非线性控制系统,针对航空器的航迹预测任务建立了多信息EKF预测模型.陈明强等[20 ] 提出了基于无迹KF的航迹预测模型, 并完成了对飞行目标的航迹预测.然而,在现实的许多目标轨迹预测任务中,一般不能预先指定运动模型,在这种情况下,卡尔曼滤波器的应用受到了严重的限制[21 -22 ] .此外,KF算法通常是在恒定加速度的假设下应用的,这也是对现实目标运动情况的粗略逼近,这样建立的算法模型对目标轨迹预测的精度有限.为了克服传统KF算法的局限性,许多学者尝试直接从训练数据中学习运动模型.利用可学习模型来学习目标运动方程, 可以避免手工设计KF转移矩阵和测量矩阵,从而提高目标轨迹预测精度. ...
基于无迹卡尔曼滤波的飞行航迹预测方法研究
1
2021
... KF算法模型是一种应用非常广泛且有效的目标轨迹预测方法.Julier等[11 ] 在1997年提出了扩展KF(extend KF, EKF)算法,该算法不仅继承了KF算法的优势,而且能够处理非线性系统模型.吕波等[19 ] 利用EKF嵌入非线性控制系统,针对航空器的航迹预测任务建立了多信息EKF预测模型.陈明强等[20 ] 提出了基于无迹KF的航迹预测模型, 并完成了对飞行目标的航迹预测.然而,在现实的许多目标轨迹预测任务中,一般不能预先指定运动模型,在这种情况下,卡尔曼滤波器的应用受到了严重的限制[21 -22 ] .此外,KF算法通常是在恒定加速度的假设下应用的,这也是对现实目标运动情况的粗略逼近,这样建立的算法模型对目标轨迹预测的精度有限.为了克服传统KF算法的局限性,许多学者尝试直接从训练数据中学习运动模型.利用可学习模型来学习目标运动方程, 可以避免手工设计KF转移矩阵和测量矩阵,从而提高目标轨迹预测精度. ...
Research on flight path prediction method based on untraced Kalman filter
1
2021
... KF算法模型是一种应用非常广泛且有效的目标轨迹预测方法.Julier等[11 ] 在1997年提出了扩展KF(extend KF, EKF)算法,该算法不仅继承了KF算法的优势,而且能够处理非线性系统模型.吕波等[19 ] 利用EKF嵌入非线性控制系统,针对航空器的航迹预测任务建立了多信息EKF预测模型.陈明强等[20 ] 提出了基于无迹KF的航迹预测模型, 并完成了对飞行目标的航迹预测.然而,在现实的许多目标轨迹预测任务中,一般不能预先指定运动模型,在这种情况下,卡尔曼滤波器的应用受到了严重的限制[21 -22 ] .此外,KF算法通常是在恒定加速度的假设下应用的,这也是对现实目标运动情况的粗略逼近,这样建立的算法模型对目标轨迹预测的精度有限.为了克服传统KF算法的局限性,许多学者尝试直接从训练数据中学习运动模型.利用可学习模型来学习目标运动方程, 可以避免手工设计KF转移矩阵和测量矩阵,从而提高目标轨迹预测精度. ...
1
... KF算法模型是一种应用非常广泛且有效的目标轨迹预测方法.Julier等[11 ] 在1997年提出了扩展KF(extend KF, EKF)算法,该算法不仅继承了KF算法的优势,而且能够处理非线性系统模型.吕波等[19 ] 利用EKF嵌入非线性控制系统,针对航空器的航迹预测任务建立了多信息EKF预测模型.陈明强等[20 ] 提出了基于无迹KF的航迹预测模型, 并完成了对飞行目标的航迹预测.然而,在现实的许多目标轨迹预测任务中,一般不能预先指定运动模型,在这种情况下,卡尔曼滤波器的应用受到了严重的限制[21 -22 ] .此外,KF算法通常是在恒定加速度的假设下应用的,这也是对现实目标运动情况的粗略逼近,这样建立的算法模型对目标轨迹预测的精度有限.为了克服传统KF算法的局限性,许多学者尝试直接从训练数据中学习运动模型.利用可学习模型来学习目标运动方程, 可以避免手工设计KF转移矩阵和测量矩阵,从而提高目标轨迹预测精度. ...
1
... KF算法模型是一种应用非常广泛且有效的目标轨迹预测方法.Julier等[11 ] 在1997年提出了扩展KF(extend KF, EKF)算法,该算法不仅继承了KF算法的优势,而且能够处理非线性系统模型.吕波等[19 ] 利用EKF嵌入非线性控制系统,针对航空器的航迹预测任务建立了多信息EKF预测模型.陈明强等[20 ] 提出了基于无迹KF的航迹预测模型, 并完成了对飞行目标的航迹预测.然而,在现实的许多目标轨迹预测任务中,一般不能预先指定运动模型,在这种情况下,卡尔曼滤波器的应用受到了严重的限制[21 -22 ] .此外,KF算法通常是在恒定加速度的假设下应用的,这也是对现实目标运动情况的粗略逼近,这样建立的算法模型对目标轨迹预测的精度有限.为了克服传统KF算法的局限性,许多学者尝试直接从训练数据中学习运动模型.利用可学习模型来学习目标运动方程, 可以避免手工设计KF转移矩阵和测量矩阵,从而提高目标轨迹预测精度. ...
基于BP神经网络的空中目标航迹预测模型
1
2017
... 可学习模型包括以神经网络为代表的机器学习方法,神经网络可通过大量数据学习数据的本质特征,其深层非线性的网络结构能够实现对复杂函数的逼近,在目标轨迹预测方面得到了广泛应用.如钱夔等[23 ] 用后向传播(back propagation, BP)神经网络对飞机航迹数据进行训练学习,实现了对飞行目标轨迹的预测,但BP神经网络比较简单,预测精度有限.吴一凡等[24 ] 提出了基于卷积神经网络的飞行航迹预测模型,根据飞行目标的高度和经、纬度信息预测飞行目标的位置信息. ...
Air target track prediction model based on BP neural network
1
2017
... 可学习模型包括以神经网络为代表的机器学习方法,神经网络可通过大量数据学习数据的本质特征,其深层非线性的网络结构能够实现对复杂函数的逼近,在目标轨迹预测方面得到了广泛应用.如钱夔等[23 ] 用后向传播(back propagation, BP)神经网络对飞机航迹数据进行训练学习,实现了对飞行目标轨迹的预测,但BP神经网络比较简单,预测精度有限.吴一凡等[24 ] 提出了基于卷积神经网络的飞行航迹预测模型,根据飞行目标的高度和经、纬度信息预测飞行目标的位置信息. ...
CNN神经网络在航迹预测中的应用
1
2019
... 可学习模型包括以神经网络为代表的机器学习方法,神经网络可通过大量数据学习数据的本质特征,其深层非线性的网络结构能够实现对复杂函数的逼近,在目标轨迹预测方面得到了广泛应用.如钱夔等[23 ] 用后向传播(back propagation, BP)神经网络对飞机航迹数据进行训练学习,实现了对飞行目标轨迹的预测,但BP神经网络比较简单,预测精度有限.吴一凡等[24 ] 提出了基于卷积神经网络的飞行航迹预测模型,根据飞行目标的高度和经、纬度信息预测飞行目标的位置信息. ...
Application of CNN neural network in track prediction
1
2019
... 可学习模型包括以神经网络为代表的机器学习方法,神经网络可通过大量数据学习数据的本质特征,其深层非线性的网络结构能够实现对复杂函数的逼近,在目标轨迹预测方面得到了广泛应用.如钱夔等[23 ] 用后向传播(back propagation, BP)神经网络对飞机航迹数据进行训练学习,实现了对飞行目标轨迹的预测,但BP神经网络比较简单,预测精度有限.吴一凡等[24 ] 提出了基于卷积神经网络的飞行航迹预测模型,根据飞行目标的高度和经、纬度信息预测飞行目标的位置信息. ...
1
... 以上所提的模型对目标轨迹预测各有优劣,但都没有利用目标轨迹数据在时序上具有的高度相关性.循环神经网络(recurrent neural network, RNN) 是一种能够提取序列数据特征的经典神经网络模型[25 ] ,但是由于RNN自身简单的网络结构对于长时间序列的记忆能力较差,Hochreiter等[26 ] 提出了由RNN改进的长短时记忆(long-short term memory, LSTM)神经网络,由于自身复杂的结构, LSTM模型能够记忆更长的序列数据中蕴含的信息,并在后续处理中加以运用,如今LSTM网络已被广泛应用在各类目标的轨迹预测任务中, 并取得了良好的效果. ...
Long short-term memory
1
1997
... 以上所提的模型对目标轨迹预测各有优劣,但都没有利用目标轨迹数据在时序上具有的高度相关性.循环神经网络(recurrent neural network, RNN) 是一种能够提取序列数据特征的经典神经网络模型[25 ] ,但是由于RNN自身简单的网络结构对于长时间序列的记忆能力较差,Hochreiter等[26 ] 提出了由RNN改进的长短时记忆(long-short term memory, LSTM)神经网络,由于自身复杂的结构, LSTM模型能够记忆更长的序列数据中蕴含的信息,并在后续处理中加以运用,如今LSTM网络已被广泛应用在各类目标的轨迹预测任务中, 并取得了良好的效果. ...
Recurrent neural net learning and vanishing gradient
2
1998
... 不同于前馈神经网络,RNN是针对于时序数据进行处理的网络模型.然而,由于梯度消失问题[27 ] ,早期的RNN模型均很难被训练.为了解决梯度消失或梯度爆炸问题,并使模型可以长期存储时间序列中的有用信息,Hochreiter等[27 ] 提出了LSTM.LSTM是RNN神经网络的一种特殊的变体,其更改了RNN的神经元结构,在神经元内部增加了遗忘门、输入门、输出门等单元,由此可以通过LSTM神经元获得长时间序列的依赖信息.LSTM的网络结构如图 1 所示. ...
... [27 ]提出了LSTM.LSTM是RNN神经网络的一种特殊的变体,其更改了RNN的神经元结构,在神经元内部增加了遗忘门、输入门、输出门等单元,由此可以通过LSTM神经元获得长时间序列的依赖信息.LSTM的网络结构如图 1 所示. ...