0 引言
信息化技术的发展和应用极大改变了当前的作战样式, 装备之间的联系越来越密切, 现代战争也更加强调两个装备体系之间的对抗, 作战过程中装备体系性能的优劣直接影响着战争的胜负。科学合理地研究装备体系对抗过程中打击或干扰对装备体系性能的潜在影响, 对优化体系结构、提高体系整体性能、针对性地指导装备建设等具有非常重要的意义。
为研究体系对抗过程中打击或干扰对装备体系性能的潜在影响, 传统研究运用可靠性评估指标来评估装备体系维持预期性能或完成使命任务的能力[1-3]; 或者运用脆弱性评估指标来评估装备体系可能受到的外部打击或干扰等的不利影响[4-5]。随着研究进一步拓展, 军事专家开始意识到, 由于外部打击或干扰是不能完全避免的, 可靠性与脆弱性指标往往只能反映某一方面的特征, 均存在一定的不足。军事专家不仅关心受到打击或干扰后装备体系性能降低的程度或保持正常性能的概率, 更关注在装备体系性能偏离正常水平后, 如何采取措施使装备体系快速有效地恢复到预期性能或预期状态。在此背景下, 军事专家逐渐使用韧性作为打击或干扰下装备体系性能的测度指标。韧性的核心内涵[6-7]包括两个方面: 其一为体系吸收打击或干扰的能力, 可通过受到外部打击或干扰后体系性能下降的程度体现; 其二为体系快速高效地从性能下降状态恢复到预期性能的能力。文献[8]借助超网络模型, 分析了军事体系的韧性并给出了定量评估军事体系韧性的指标, 但给出的韧性指标不够全面,并且未涉及对韧性评估方法的探讨。文献[9]对Cyber攻击下的军事信息系统提出了能力评估方法, 建立了15项韧性能力度量指标和韧性能力指标评估计算模型, 但韧性指标的选取未考虑累计损失的制约因素。文献[10]按照作战过程中体系性能的变化, 提出了体系韧性评估方法, 并开展了基于韧性的作战网络节点重要度分析, 但未考虑攻击后的恢复策略。文献[11]给出了一种面向任务的韧性评估框架, 从时间韧性和性能韧性两个维度对系统的综合韧性进行度量, 但对恢复策略的设计缺乏讨论。
以上工作为装备体系韧性的研究奠定了基础, 但综合来看, 关于装备体系韧性的研究尚处于起步阶段, 在以下方面仍然存在一定的不足: ①针对装备体系韧性没有给出明确的定义, 以及如何定量评估其韧性; ②如何站在韧性的角度识别装备体系作战网络中的关键单元, 以优化体系结构, 减少打击或干扰对装备体系的不良影响; ③在打击或干扰事件影响多个作战网络链路时, 依靠经验性恢复策略仅能得到次优甚至严重偏离预期的方案, 如何构建合理的恢复策略, 使装备体系性能快速有效恢复,仍需要进一步探讨。
针对以上问题, 本文首先分析了装备体系的韧性及其受到打击或干扰后的性能变化的过程, 建立了量化装备体系韧性的数学模型; 其次, 提出了韧性增加值链路重要度指标, 并借助作战环理论对装备体系作战网络链路开展重要度评估, 找出体系结构优化的重点环节; 然后, 构建了不同的恢复策略, 通过计算分析确定了最佳策略, 为保障和提高体系作战性能指明了方向; 最后通过应用案例验证了所提方法与模型的适用性和合理性。
1 装备体系韧性
装备体系是指在面向特定使命任务时, 由功能上相互关联、性能上相互补充的各种装备系统, 按照一定的结构综合集成的更高层次的装备系统[12]。信息化战争的战场对抗环境瞬息万变, 装备体系作为一类特殊的体系, 其面临的战场对抗环境更加复杂。在体系对抗过程中, 装备体系的性能可能与预期性能出现差距, 需要其在组成上或结构上进行相应调整。因此, 装备体系本身及其受到打击或干扰后的实际性能的变化直接影响了作战使命完成情况的好坏。
为了表征打击或干扰对装备体系性能的影响, 本文将复杂系统研究中的韧性一词引入到装备体系中。韧性一词起源于拉丁语的resiliere, 意为反弹、跳回的动作。韧性在不同领域的应用问题中具有不同的概念和含义[13-18], 但都是从系统角度出发。而装备体系不同于一般的系统集成, 其更加注重装备之间的互联互通、协同配合、互相操作, 以及在同一任务的目标牵引下的组织协同。装备体系可将传统集各种功能于一体的装备拆散成功能模块, 将其进行再分布式部署, 使得针对任一模块的攻击都无法摧毁整个体系, 而且可以根据受损情况对装备体系进行动态调整, 从而难以破坏装备体系的原有功能, 形成强大韧性, 以满足作战需求[19-20]。韧性体现了体系的综合性能[21], 可以全面描述装备体系吸收打击或干扰、并从打击或干扰中恢复的能力, 是评估和优化装备体系的重要依据。
定义1 装备体系韧性是指装备体系在受到打击或干扰后, 维持预期性能的能力。
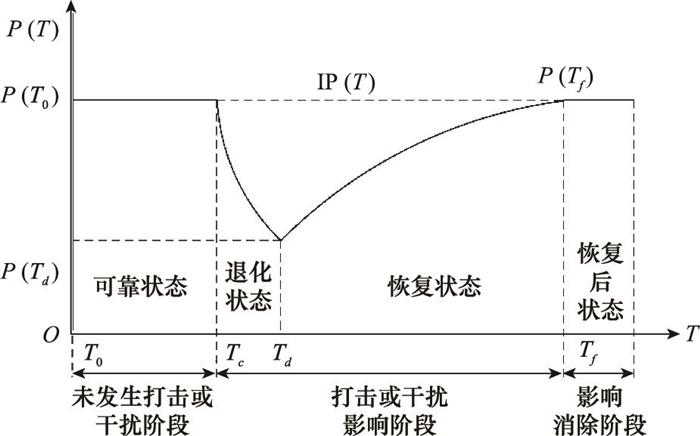
打击或干扰事件下装备体系状态变化如图 1所示, T0, Te, Td和Tf分别表示初始时刻、打击或干扰发生时刻、装备体系性能退化到最低程度的时刻, 以及装备体系性能恢复到预期状态的时刻; P(T0), P(Te), P(Td)和P(Tf)分别表示T0, Te, Td和Tf时刻的装备体系性能。因此, 可将打击或干扰事件下装备体系的状态变化分为3个阶段、4种状态,即3个阶段分别为未发生打击或干扰阶段(T≤Te), 打击或干扰影响阶段(Te≤T≤Tf), 打击或干扰影响消除阶段(Tf≤T); 4种状态分别为可靠状态、退化状态、恢复状态和恢复后状态。
图1
图1
打击或干扰事件下装备体系状态变化示意图
Fig.1
Equipment system-of-systems state transitions subjected to an attack or interference event
式中: T为度量时间段; P(T)为实际性能参数随时间T的变化情况; IP(T)表示理想中性能参数的变化情况。
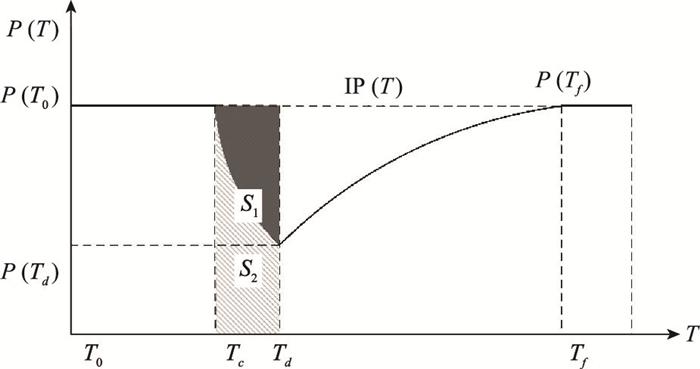
根据式(1)进行分析可知, 分母表示的是从Te到T时刻装备体系期望达到的理想累积性能, 分子表示的是从Te到T时刻装备体系的累积性能。R(T)的物理内涵可以表示为图 2中浅色区域面积S2与整体阴影区域面积的S1的比值(其中,整体阴影区域面积包括浅色区域面积S2), 即体系实际性能P(T)随时间的积分与体系理想性能IP(T)随时间的积分比。
图2
2 基于装备体系韧性的作战网络链路重要度评估模型
2.1 基于作战环的装备体系作战网络模型构建
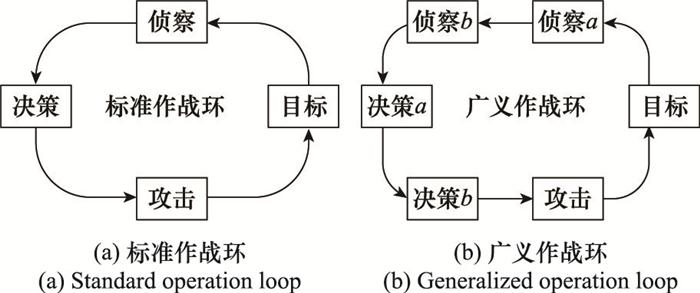
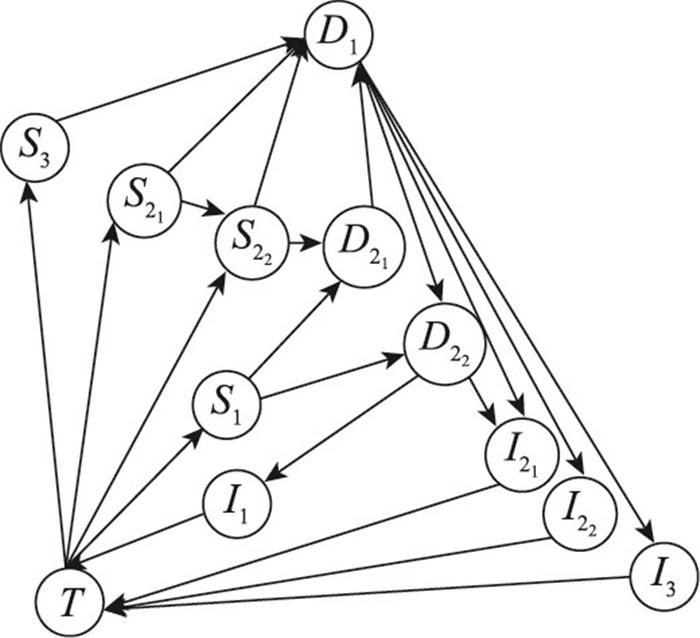
准确构建符合战争实际的装备体系作战网络模型, 是韧性分析和链路重要度评估的基础。目前, 对装备体系网络化建模的理论研究大多是基于现代作战循环理论(observe,orient,decide,act, OODA)开展的, 国内外学者主要通过作战环将装备体系抽象为要素和关系的复杂网络模型。因此, 本节基于作战环的思想, 充分考虑装备体系中装备间的关联关系, 构建装备体系作战网络模型。
2.1.1 作战网络节点建模
作战网络节点建模是以敌方目标集合为中心, 根据装备在装备体系中的功能作用, 将其抽象为作战网络节点的过程。按照装备在作战过程中功能作用或兵力角色的不同, 将作战网络中的各个节点划分为侦察节点(S)、决策节点(D)、打击节点(I)和敌方目标节点(T)4种类型。
(1) 侦察节点(S): 在战场上执行搜索、识别及获悉敌情等任务的装备实体, 如侦察机、雷达、天基侦察监视系统等。
(2) 决策节点(D): 在战场上执行信息传输和分析、指挥控制、辅助决策等任务的装备实体, 如指挥控制系统、地面指控中心、作战管理中心等。
(3) 打击节点(I): 在战场上执行火力打击及电磁干扰等任务的装备实体,如导弹、轰炸机、电磁干扰雷达等。
(4) 敌方目标节点(T): 在战场上为完成我方作战任务需打击或干扰的敌方目标实体, 如敌方的侦察、指控、打击实体、基础设施等。
2.1.2 作战网络链路建模
图3
作战网络链路建模是指将装备体系中各类装备实体之间的物质、信息或能量流的关联关系抽象为作战网络链路的过程。本节对各链路所代表的关联关系进行描述和建模, 主要包括6类链路。
(1) 目标侦察链路T→S。表示在战场上敌方目标情报信息被我方侦察节点获取识别, 为从敌方目标节点(T)指向侦察节点(S)的链路。
(2) 信息共享链路S→S。表示在战场上我方侦察节点之间进行信息的交换共享, 为从一个侦察节点(S)指向另一个侦察节点(S)的链路。
(3) 传送情报链路S→D。表示在战场上我方侦察节点向我方决策节点传送情报数据, 为从侦察节点(S)指向决策节点(D)的链路。
(4) 作战协同链路D→D。表示在战场上我方低层级决策节点向高层级决策节点请示汇报、高层级决策节点向低层级决策节点下达命令、同层级决策节点间进行信息交流, 为从一个决策节点(D)指向另一个决策节点(D)的链路。
(5) 指挥决策链路D→I。表示在战场上我方决策节点向我方打击节点下达命令指示, 为从决策节点(D)指向打击节点(I)的链路。
(6) 目标打击链路I→T。表示在战场上我方打击节点对敌方目标实施攻击或干扰, 为打击节点(I)指向敌方目标节点(T)的链路。
2.2 作战环标准长度和作战环广义长度
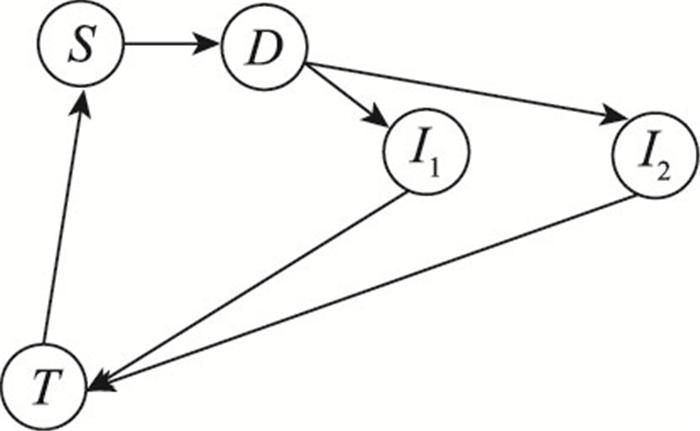
由于作战环中各链路的形成为作战网络中节点之间的物质、信息或能量流作用的结果, 因此可用链路长度来量化节点之间的相互作用关系的强弱, 链路长度受到两端装备性能的影响, 支撑装备的性能越高, 链路长度越短, 节点之间的相互作用关系越强。例如,打击装备性能越强, 目标打击链路I→T长度越短, 成功击毁敌方目标的可能性越大, 侦察和决策装备同理。如图 4所示, 同为打击节点的I1相比于打击节点I2的综合性能(如打击速度、打击精度)更好, 前者的目标打击链路长度应该比后者短。
图4
以上表明,即使侦察节点、决策节点、打击节点、敌方目标节点的数量都为1, 由于装备的性能不同, 作战环的长度也存在着不同。基于此, 本文对作战环长度进行了分类并定义如下:
定义2 作战环标准长度是指作战环中节点间的链路长度之和, 且每个链路的长度都是1。
例如: 对于作战环T→S→D→I→T, 链路“→”的数量为4, 则此作战环标准长度为4。
定义3 作战环广义长度是指作战环中节点间的链路长度之和, 且每个链路的长度需要根据实际作战情况中的两端装备性能确定。
例如: 对于作战环T→S→D→I→T, 若目标侦察链路T→S的长度LT→S为2, 传送情报链路S→D的长度LS→D为3, 指挥决策链路D→I的长度LD→I为1, 目标打击链路I→T的长度LI→T为4, 则此作战环的广义长度为10。
如考虑信息共享链路S→S和作战协同链路D→D, 则具体表达式为
根据定义2和定义3可知, 目标侦察、情报传送、指挥决策、目标打击链路的长度均为1时, 两者长度相同, 因而作战环标准长度只是作战环广义长度的一个特例, 采用作战环广义长度描述作战环更具一般性, 说明了本文对作战环标准长度和作战环广义长度的分类和定义合理有效。
2.3 链路重要度评估
装备体系网络化建模是装备体系结构优化的基础, 以此为基础构建链路重要度评估模型, 可更加有效地研究装备实体之间的关联关系对装备体系性能的影响[12]。为提高作战网络的韧性, 降低打击或干扰事件对作战网络性能的影响, 本节通过作战环链路长度的变化来确定作战网络链路的重要程度, 以便有针对性地改进作战网络的性能。
2.3.1 作战环性能计算
目前, 最常用的衡量作战网络性能的指标是能力需求满足度, 其主要侧重于任务完成概率或程度方面。然而, 在真实作战过程中,往往对完成使命任务的时间存在要求, 一旦在规定时间内没有完成使命任务, 即使后续完成任务的概率或程度达到100%, 也认为本次任务不完全成功[29]。考虑执行作战任务的时间要求, 计算完成某个作战环所需的作战环时间为
式中: top表示完成作战环所用的时间, 即作战环时间; Lop表示作战环广义长度; ${\bar v}$表示侦察、决策、打击的平均作战速度。
可以这样认为, 作战环时间可用来衡量其作战效果, 作战时间越短, 作战环性能越好; 实际作战时间越长, 作战环性能越差。据此, 给出作战环时间效能指标来衡量作战环性能, 计算模型如下:
式中: Eop表示作战环时间效能。
2.3.2 作战环数量计算
当前,对作战环数量的具体计算可通过作战网络的邻接矩阵[28]来确定。假设作战网络中有N个节点, 则其邻接矩阵为A=[aij]N×N。其中:
根据邻接矩阵的幂运算可知, aiil为经过节点i的长度为l的作战环数量, l为标准长度, 所以作战环数量Nop的计算如下所示:
然而在求和过程中, 没有排除作战环会被重复计算的情况, 此时计算过程会受到重复无效作战环的影响, 这是不能被忽略的。因此, 本文参考文献[30]对作战环数量的计算方法进行改进,以获得正确的作战环数量。
2.3.3 作战网络性能的计算
作战网络包含众多的作战环, 可以通过评价作战网络中作战环数量和性能的方式来评价作战网络的性能。假设作战网络性能由各个作战环性能的综合作用影响, 用所有作战环性能的平均值来衡量。已知各个作战环的作战环性能和作战环数量, 则作战网络性能的计算如下所示:
式中: m表示第m个作战环; Nop表示作战环数量; Eopm表示第m个作战环的性能。
一般情况下, 作战环广义长度越长, 可靠性也越低, 在作战网络中应该尽量避免使用这种较长的作战环。因此, 应考虑对作战环的性能进行加权, 即对越长的环, 所赋权重越低, 以降低较长作战环对作战网络性能的影响。权重cLop可以根据实际情况确定, 只要遵循越长的作战环赋予的权重越低的原则即可。这里可令cLop =1/Lop, 故某时刻考虑了环的长度进行加权后的作战网络性能为
当作战环广义长度Lop较长时, 1/Lop→0, 作战环对作战网络性能的影响可以忽略不计。
将式(8)代入式(1), 即可求得装备体系作战网络韧性指标。
2.3.4 基于韧性增加值的作战网络链路重要度评估
因此, 本文以链路长度增加的形式将打击或干扰事件引入到作战网络中, 提出了基于韧性增加值的链路重要度指标, 定义为
式中: LIMi→j(Td)表示链路i到j的重要度指标; R(Td|Li→j(Td)=Li→j)表示假定链路i到j不受打击或干扰的前提下Td时刻作战网络的韧性; R(Td)表示Td时刻实际的作战网络韧性。显然, LIMi→j(Td)的内涵是从Te到Td时刻链路i到j不受打击或干扰影响(完好无损)时的装备体系作战网络韧性的相对增加值。
考虑在实际作战过程中, 作战环的广义长度一般不会无限长, 且即使存在过长的作战环, 由于可靠性和时效性较低, 其对作战效果的影响也较小。一般情况下, 当链路遭受打击或干扰时, 链路长度的增加不超过100%。
3 作战网络的恢复策略
提高装备体系韧性的关键在于设计和选择合适的恢复策略,使作战网络性能得到恢复。在实际战场中, 打击或干扰往往会影响作战网络中的多个链路, 此时链路的修复顺序决定着作战网络性能的恢复效果。本文结合作战环的相关理论研究成果, 以作战网络中的故障链路为修复对象, 以作战网络性能恢复为依据, 构建不同的恢复策略,以研究不同故障链路修复顺序对作战网络性能恢复的影响。
3.1 作战网络的恢复策略构建
现令初始作战网络为G, 其邻接矩阵为A, 遭受打击或干扰的故障链路数量为Y。本文构建随机恢复策略(random recovery strategy, RRS)、最大作战环数量恢复策略(maximum operation loop number first recovery strategy, MOLNFRS)和最大链路重要度恢复策略(maximum link importance first recovery strategy, MLIFRS)3种策略。
3.1.1 RRS
RRS是指在非完全信息条件下, 随机选取作战网络中的故障链路进行修复的一种策略。
假设需对作战网络G中的Y个故障链路实施RRS, 并评估各个故障链路修复完成时的作战网络性能, 其基本步骤如下。
步骤1 对作战网络G中的Y个故障链路按照随机选择的顺序进行修复, 直至Y个故障链路修复完成,每个故障链路修复完成时, 都会得到一个新的作战网络。
步骤2 计算作战网络性能恢复过程中各个故障链路修复完成时新的作战网络性能。
3.1.2 MOLNFRS
MOLNFRS是指在完全信息下, 优先选择构成作战环数量最多的故障链路进行修复, 并对新的作战网络循环此修复策略, 直至Y个故障链路修复完成。
假设需对作战网络G中的Y个故障链路实施MOLNFRS, 并评估各个故障链路修复完成时的作战网络性能, 其基本步骤如下。
步骤1 分析每个故障链路构成的作战环数量, 并按照作战环数量从多到少的顺序进行排序。
步骤2 根据排序结果, 优先选择构成作战环数量最多的故障链路进行修复, 直至Y个故障链路修复完成,每个故障链路修复完成时, 都会得到一个新的作战网络。
步骤3 计算作战网络性能恢复过程中各个故障链路修复完成时新的作战网络性能。
3.1.3 MLIFRS
MLIFRS是指在完全信息下, 优先选择重要度最大的故障链路进行修复, 并对新的作战网络循环此修复策略, 直至Y个故障链路修复完成的一种策略。
假设需对作战网络G中的Y个故障链路实施MLIFRS, 并评估各个链路修复完成时的作战网络性能, 其基本步骤如下。
步骤1 根据上述所提方法计算故障链路的重要度, 并按照链路重要度从大到小的顺序进行排序。
步骤2 根据排序结果, 优先选择重要度最大的故障链路进行修复, 直至Y个故障链路修复完成, 每个故障链路修复完成时, 都会得到一个新的作战网络。
步骤3 计算作战网络性能恢复过程中各个故障链路修复完成时新的作战网络性能。
3.2 作战网络的恢复策略选择
假设破坏或干扰使作战网络的X个链路中的Y个链路发生故障, 恢复策略从Td时刻依次修复故障链路, 直至Tf时刻所有链路修复完成。在链路修复过程中, 考虑链路修复顺序的多种组合, 恢复策略可表示为不同链路修复顺序[33]的集合: Wp={B1, B2, …BH, …, BY}, p=1, 2, …,CXY。其中, BH表示修复顺序为H的故障链路。在作战网络性能恢复的过程中, 恢复策略决定作战网络性能恢复的速度和程度。因此, 为了度量不同恢复策略对装备体系性能恢复的影响, 引入性能恢复指数Rec,如下所示:
式中: P(T)表示任意时刻的作战网络性能; Rec表示作战网络性能的累计恢复。
性能恢复指数衡量了作战网络性能恢复过程中, 多个故障链路修复给作战网络整体带来的规模效益, 该指标既反映了作战网络性能恢复的时间, 也综合体现了作战网络性能恢复的程度。通过对比不同恢复策略下的性能恢复指数, 可以确定作战网络性能恢复最优的恢复策略, 从而提高作战网络韧性, 使作战网络在遭受攻击或干扰时能够快速和有效地恢复性能。
4 案例分析
图5
4.1 作战网络中的链路长度
综合考虑作战中所面临的战略威胁和装备实体之间的关联, 给出链路长度值如表 1所示, 本文对链路长度值的获取不进行具体论述。
表1 作战网络中各个链路的长度
Table 1
| 编号 | 链路 | 长度 | 编号 | 链路 | 长度 | |
| 1 | T→S1 | 3 | 10 | D1→I3 | 5 | |
| 2 | T→S2 | 6 | 11 | D1→D2 | 1 | |
| 3 | T→S3 | 7 | 12 | D2→I1 | 4 | |
| 4 | S1→D2 | 3 | 13 | D2→I2 | 2 | |
| 5 | S2→D1 | 2 | 14 | D2→D1 | 1 | |
| 6 | S2→D2 | 2 | 15 | I1→T | 2 | |
| 7 | S2→S2 | 1 | 16 | I2→T | 6 | |
| 8 | S3→D1 | 3 | 17 | I3→T | 7 | |
| 9 | D1→I2 | 4 | — | — | — |
4.2 作战网络性能
在计算作战网络性能前, 计算作战网络中每个作战环的性能, 假设侦察、决策、打击的平均作战速度为${\bar v}$,${\bar v}$=1, 则每个作战环的性能如表 2所示。
表2 作战网络中各个作战环的性能
Table 2
| 编号 | 装备构成 | 作战环广义长度 | 作战环时间 | 作战环性能 |
| 1 | T, S1, D2, I1 | 12 | 12 | 0.402 |
| 2 | T, S1, D2, I2 | 14 | 14 | 0.379 |
| 3 | T, S2, D1, I2 | 18 | 18 | 0.346 |
| 4 | T, S2, D1, I2 | 18 | 18 | 0.346 |
| 5 | T, S2, D1, I3 | 20 | 20 | 0.334 |
| 6 | T, S2, D1, I2 | 18 | 18 | 0.346 |
| 7 | T, S2, D1, I2 | 18 | 18 | 0.346 |
| 8 | T, S2, D1, I3 | 20 | 20 | 0.334 |
| 9 | T, S3, D1, I2 | 20 | 20 | 0.334 |
| 10 | T, S3, D1, I2 | 20 | 20 | 0.334 |
| 11 | T, S3, D1, I3 | 22 | 22 | 0.324 |
| 12 | T, S2, S2, D1, I2 | 19 | 19 | 0.340 |
| 13 | T, S2, S2, D1, I2 | 19 | 19 | 0.340 |
| 14 | T, S2, S2, D1, I3 | 21 | 21 | 0.328 |
| 15 | T, S1, D2, D1, I2 | 17 | 17 | 0.353 |
| 16 | T, S1, D2, D1, I2 | 17 | 17 | 0.353 |
| 17 | T, S1, D2, D1, I3 | 19 | 19 | 0.340 |
| 18 | T, S2, D2, D1, I2 | 19 | 19 | 0.340 |
| 19 | T, S2, D2, D1, I2 | 19 | 19 | 0.340 |
| 20 | T, S2, D2, D1, I3 | 21 | 21 | 0.328 |
| 21 | T, S2, D1, D2, I3 | 15 | 15 | 0.369 |
| 22 | T, S2, D1, D2, I2 | 17 | 17 | 0.353 |
| 23 | T, S2, D1, D2, I1 | 15 | 15 | 0.369 |
| 24 | T, S2, D1, D2, I2 | 17 | 17 | 0.353 |
| 25 | T, S2, D1, D2, I1 | 17 | 17 | 0.353 |
| 26 | T, S3, D1, D2, I2 | 19 | 19 | 0.340 |
| 27 | T, S2, S2, D2, D1, I2 | 20 | 20 | 0.334 |
| 28 | T, S2, S2, D2, D1, I2 | 20 | 20 | 0.334 |
| 29 | T, S2, S2, D2, D1, I3 | 22 | 22 | 0.324 |
| 30 | T, S2, S2, D1, D2, I1 | 16 | 16 | 0.361 |
| 31 | T, S2, S2, D1, D2, I2 | 18 | 18 | 0.346 |
| 32 | T, S1, D2, D1, D2, I1 | 14 | 14 | 0.379 |
| 33 | T, S2, D2, D1, D2, I1 | 16 | 16 | 0.361 |
| 34 | T, S2, D2, D1, D2, I2 | 18 | 18 | 0.346 |
| 35 | T, S1, D2, D1, D2, I2 | 16 | 16 | 0.361 |
| 36 | T, S2, S2, D2, D1, D2, I1 | 17 | 17 | 0.353 |
| 37 | T, S2, S2, D2, D1, D2, I2 | 19 | 19 | 0.340 |
通过对作战网络的邻接矩阵进行分析, 确定装备体系作战网络中的作战环的数量为37;作战网络性能由各个作战环性能综合作用影响, 考虑了环的长度, 进行加权后的此作战环的网络性能为0.019 7。
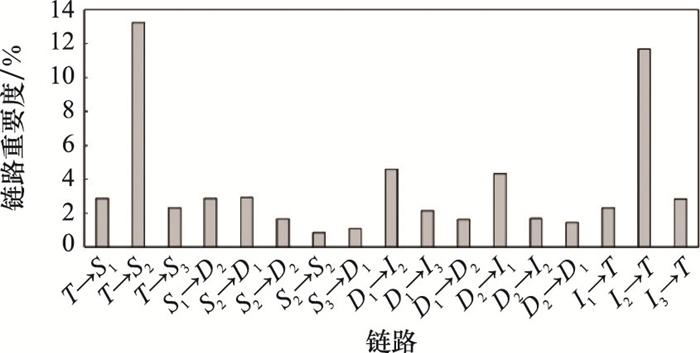
4.3 作战网络链路的重要度评估
表3 链路重要度及排序结果
Table 3
| 编号 | 链路 | 构成作战环数量 | 受到打击或干扰后的作战网络性能/% | 链路重要度/% | 排序 |
| 1 | T→S1 | 7 | 1.908 | 2.879 | 7 |
| 2 | T→S2 | 25 | 1.697 | 13.234 | 1 |
| 3 | T→S3 | 5 | 1.920 | 2.329 | 9 |
| 4 | S1→D2 | 7 | 1.908 | 2.879 | 6 |
| 5 | S2→D1 | 15 | 1.906 | 2.942 | 5 |
| 6 | S2→D2 | 10 | 1.935 | 1.663 | 13 |
| 7 | S2→S2 | 10 | 1.954 | 0.856 | 17 |
| 8 | S3→D1 | 5 | 1.948 | 1.122 | 16 |
| 9 | D1→I2 | 14 | 1.870 | 4.585 | 3 |
| 10 | D1→I3 | 7 | 1.924 | 2.149 | 11 |
| 11 | D1→D2 | 14 | 1.935 | 1.659 | 14 |
| 12 | D2→I1 | 8 | 1.876 | 4.319 | 4 |
| 13 | D2→I2 | 8 | 1.934 | 1.699 | 12 |
| 14 | D2→D1 | 15 | 1.940 | 1.469 | 15 |
| 15 | I1→T | 8 | 1.920 | 2.315 | 10 |
| 16 | I2→T | 22 | 1.726 | 11.683 | 2 |
| 17 | I3→T | 7 | 1.908 | 2.855 | 8 |
图6
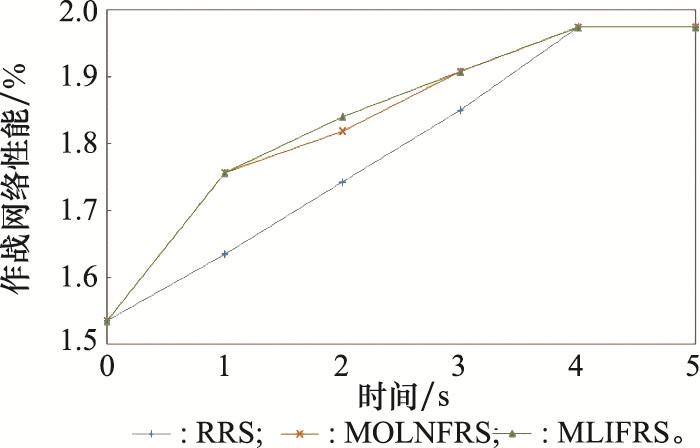
4.4 恢复策略选择
为分析和比较不同恢复策略对作战网络性能恢复的影响, 本文通过对比3种不同策略下作战网络性能恢复曲线和性能恢复指数Rec, 从而确定最优恢复策略。假设Te时刻链路T→S1、链路S2→D1、链路D2→I1和链路I2→T同时受到打击或干扰, 从Td开始立刻依次修复链路, 且修复所需时间相同。
表4 作战网络性能恢复详情
Table 4
| 时间 | RRS | MOLNFRS | MLIFRS |
| 0 | 1.535 | 1.535 | 1.535 |
| 1 | 1.635 | 1.757 | 1.757 |
| 2 | 1.743 | 1.819 | 1.840 |
| 3 | 1.850 | 1.908 | 1.908 |
| 4 | 1.974 | 1.974 | 1.974 |
| 5 | 1.974 | 1.974 | 1.974 |
图7
图7
作战网络性能恢复曲线对比
Fig.7
Comparison of performance recovery curve of operation network
5 结束语
装备体系韧性分析作为一项全新、复杂的工程, 为指挥人员提供了一种新的体系优化思路和分析角度。本文从装备体系的相关理论出发, 针对装备体系韧性提出了一种量化方法, 主要贡献如下:
(1) 全面考虑了打击或干扰事件下装备体系性能退化与恢复的全过程, 对应提出并定义了装备体系韧性概念, 为分析和评价装备体系提供了新的思路。
(2) 从韧性增加值的角度出发, 提出了一种链路重要度的评估指标, 构建了基于装备体系韧性的作战网络链路重要度评估模型, 有助于提高作战网络韧性以及优化体系结构。
(3) 比较分析了作战网络链路出现故障后不同恢复策略对作战网络性能恢复的影响, 结果证明了提出的MLIFRS可以优先识别主要链路, 快速有效恢复作战网络性能, 可为保障和提高体系作战性能指明方向。
本文工作是对装备体系韧性研究的一次有益尝试, 可为进一步开展基于装备体系韧性的作战网络应用研究提供参考借鉴。在下一步工作中, 将考虑作战网络性能参数和网络拓扑参数相结合的装备体系韧性评估, 并以此为基础开展网络链路重要度和恢复策略研究, 以更好地服务于战场态势判断和分析, 保证作战任务的顺利实施。
参考文献
基于作战环的航空武器装备体系贡献率评估
[J].
Aviation armament system of systems contribution evaluation based on operation loop
[J].
Research on functional robustness of heterogeneous combat networks
[J].DOI:10.1109/JSYST.2018.2828779
A prototype method to rate the link vulnerability of strategic rural roads
[J].
Comparison of vulnerabi-lity analysis and live fire test and evaluation of weapon system components using COVART
[J].DOI:10.3795/KSME-A.2020.44.11.795 [本文引用: 1]
Resi-lience engineering: current status of the research and future challenges
[J].
Review of studies on the resilience of urban critical infrastructure networks
[J].DOI:10.1016/j.ress.2019.106617 [本文引用: 1]
基于超网络的军事体系韧性评估
[J].
Evaluating military system of systems resilience using super networks
[J].
Cyber攻击下韧性信息服务云环境能力评估
[J].
Evaluating the capability for resilient information service cloud environment under Cyberattack condition
[J].
Resilience based importance measure analysis for SoS
[J].DOI:10.21629/JSEE.2019.05.10 [本文引用: 2]
面向任务的复杂系统韧性评估方法
[J].
Mission-oriented resilience evaluation method for complex system
[J].
基于武器装备体系作战网络模型的装备贡献度评估
[J].
Equipment contribution degree evaluation method based on combat network of weapon system-of-systems
[J].
Resilience in trans portation systems: a systematic review and future directions
[J].DOI:10.1080/01441647.2017.1383532 [本文引用: 1]
Framework for analytical quantification of disaster resilience
[J].
Resilience and stability of ecological systems
[J].
Four concepts for resilience and the implications for the future of resilience engineering
[J].
Review of quantitative methods for supply Chain resilience analysis
[J].
Resilience oftransportation systems: concepts and comprehensivereview
[J].
Efficient availability assessment of reconfigurable systems with interdependencies
[J].
Resilience in engineered resilient systems
[J].
Engineered resilient systems: a DoD perspective
[J].
Resilience of and recovery strategies for weighted networks
[J].
考虑动态重构的装备体系可用性及弹性分析
[J].
Performance availability and resilience analysis of weapon system of systems considering dynamic reconfiguration
[J].
地铁网络服务韧性评估与最优恢复策略
[J].
Evaluation and optimal recovery strategy of metro network service resilience
[J].
Lifecycle operational resilience assessment of urban water distribution networks
[J].
武器装备体系网络化描述与建模方法
[J].
Research on networked description and modeling methods of armament system-of-systems
[J].
编队对地攻击作战效能评估指标体系
[J].
Research on the index system of operational effectiveness evaluation for formation attaching ground targets
[J].
基于作战环的武器装备体系贡献度评估
[J].
Armament system of systems contribution evaluation based on operation loop
[J].
Resilience-based component importance measures
[J].
Resilience-based component importance measures for critical in frastructure network systems
[J].
基于弹性的体系组件重要度及恢复策略
[J].
Resilience-based component importance and recovery strategy for system-of-systems
[J].