0 引言
无人机系统的快速发展给未来低空空域的建设带来了新的机遇和挑战[1]。无人机进入的领域越来越广, 发挥的作用越来越大, 特别是在执行4D(dangerous, dirty, dull, deep)任务时, 无人机往往是被优先考虑的对象。由此可见, 无人机作为低空空域内运行的重要主体, 其安全、有序、高效的运行, 产生的风险最小至关重要, 而无人机安全间隔标定技术是实现无人机在低空空域内安全、高效运行的关键手段和核心支撑, 因此研究无人机的碰撞风险和安全间隔具有重要意义。
在有人机碰撞风险和安全间隔的研究方面, Reich提出了经典的Reich[2-4]模型, 该模型主要基于航空器位置与速度的随机偏差假设, 量化了航空器在航路上的碰撞风险。后来, 众多学者在该模型的基础上, 对模型做出了改进和优化。文献[5-9]考虑了航空器尺寸、导航性能、飞行速度等因素, 分别针对平行航路、交叉航路、平行跑道和单跑道的情形, 共同建立了多因素融合的高空航空器碰撞风险模型。中国民航大学的张兆宁等[10-13]针对自由飞行条件下航空器碰撞风险评估技术开展了一系列研究工作, 分析了包含通信导航监视、人为因素在内的影响航空器碰撞风险的主要因素, 建立了自由飞行环境下航空器碰撞风险评估模型, 从而确定了航空器在日常飞行活动中应当满足的目标安全水平。
在无人机碰撞风险和安全间隔的研究方面, Zou等[14]针对多旋翼无人机在固化空域中的飞行场景, 基于拉盖尔多项式与单变量条件逼近法, 推导了基于航迹误差的无人机碰撞概率快速求解算法。Lee等[15]建立了基于三维高斯分布的无人机空中碰撞风险模型, 并通过雷达数据对模型的有效性进行了验证。文献[16-19]针对无人机与有人机之间的碰撞风险问题进行了一系列研究, 通过Petri网等方式对无人机飞行安全评估的过程进行建模, 计算了特定类无人机与运输类飞机之间的空中碰撞概率。Mcfadyen等[20]通过统计分析真实的雷达数据, 计算了无人机与有人机的碰撞概率。邓力[21]针对机场终端区内无人机与民航客机混合运行的情况, 考虑航空器位置误差和体积因素, 建立了无人机与有人机碰撞概率模型。Weinert等[22]研究了中小型无人机应当遵循的自主间隔模型, 最终得出的水平间隔为2 000 ft, 垂直间隔为250 ft。Chen等[23]研究结论为了装载有两种不同导航设备的无人机自主间隔, 最终得出的结论为水平间隔为2 200 ft, 垂直间隔为250 ft。文献[24]研究了城市低空环境下无人机飞行冲突数与安全间隔之间的关系。Weibel等[25]提出了一种基于蒙特卡罗仿真的无人机间隔标准的制定方法, 最终得出无人机在3个方向上的安全间隔分别为纵向8 000 ft, 侧向3 000 ft, 垂直300 ft。
纵观现有研究成果, 目前该领域中的大多数研究主要聚焦于如何更好地将无人机系统融入现有国家空域系统, 已经针对无人机与有人机之间的关系进行了详细的探讨, 初步奠定了一定的研究基础。然而, 目前少有针对无人机与无人机之间、尤其是多旋翼无人机之间安全间隔的研究, 该领域几乎是空白。因此, 为解决以上问题, 本文以自由空域为背景, 以多旋翼无人机为研究对象, 提出一种自由空域下多旋翼无人机安全间隔标定方法, 以保障无人机在低空空域中的安全、有效运行。
1 无人机碰撞盒
1.1 碰撞盒定义
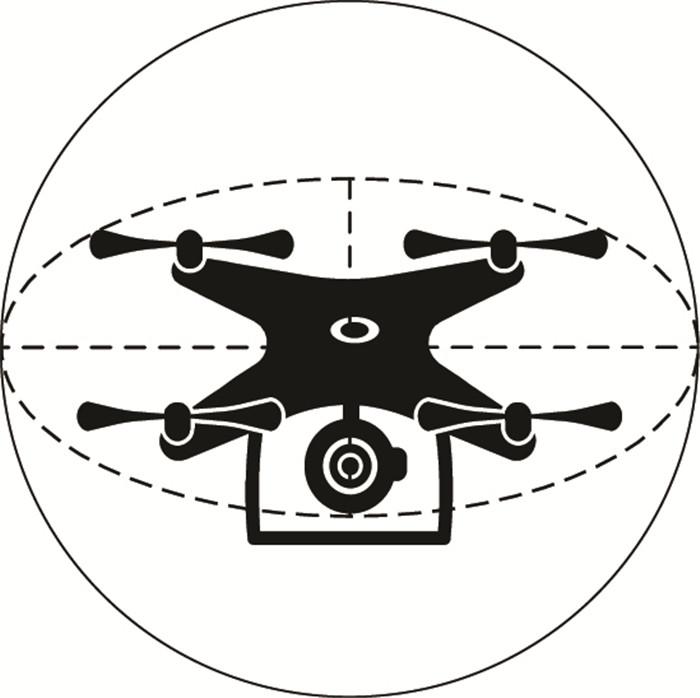
图1
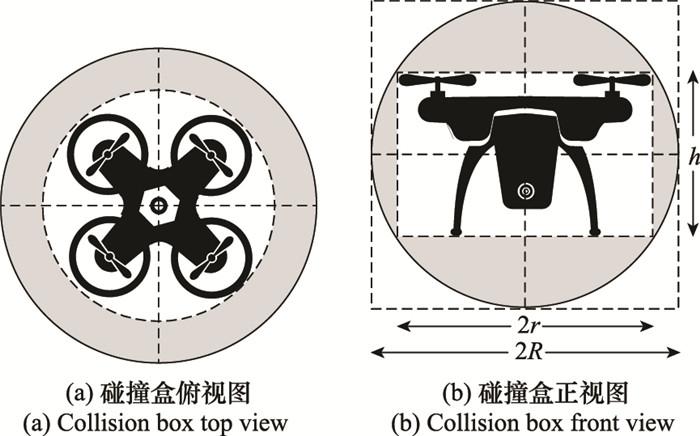
图2
设无人机水平尺寸最大值为2r, 则其对应机体圆柱半径为r, 高度为2h, 外接球体半径为R, 由立体几何知识可得
根据式(1), 即可求出无人机机体圆柱的最小外接球半径。因此, 在后续计算中可将该最小外接球作为无人机的碰撞区域。
1.2 组合碰撞区域
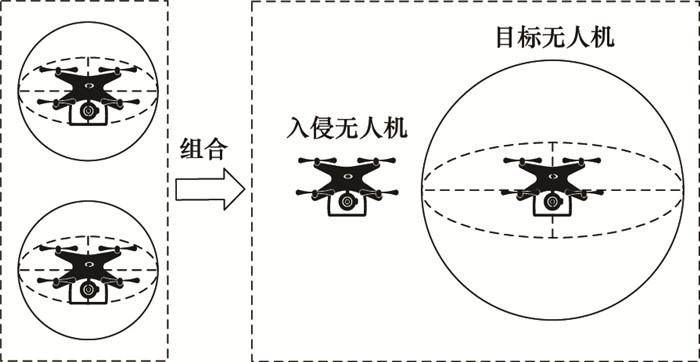
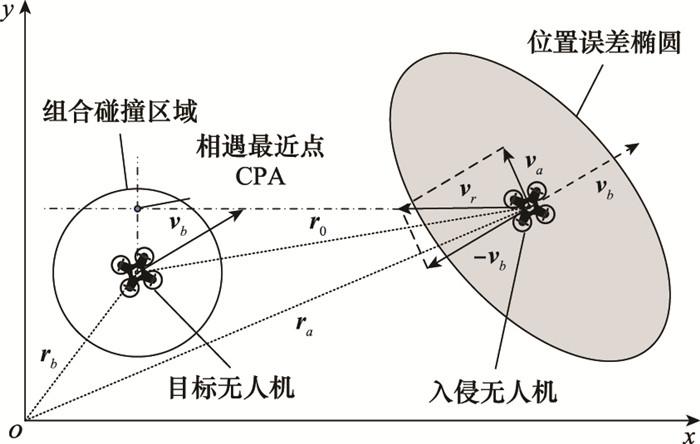
对于两架在空中相遇的无人机而言, 在计算其碰撞概率时, 为简化计算, 可以将两架无人机各自的碰撞保护区全部“转移”到某一架无人机上, 使得这架无人机带有两架无人机的组合碰撞区域, 这样另一架无人机在计算时就可以作为质点。因此, 分别定义目标无人机和入侵无人机, 如图 3所示。
图3
图3
组合碰撞区域示意图
Fig.3
Schematic diagram of combined collision zone for unmanned aerial vehicle
目标无人机是碰撞概率计算中的主要研究对象, 该无人机带有两架无人机的组合碰撞保护区, 保护区半径为两架无人机各自的保护区球体半径之和; 入侵无人机是对目标无人机构成入侵威胁的无人机, 在计算碰撞概率时可以将其视为质点。另外, 考虑两架无人机各自位置误差对碰撞概率产生的影响, 本文将两架无人机的组合位置误差全部分配给入侵无人机, 使得目标无人机的位置确定, 入侵无人机的位置带有不确定性。由上述概念可知, 当目标无人机和入侵无人机的相对距离小于目标无人机组合碰撞区域的球体半径时, 就可以认为两架无人机发生了碰撞。
2 无人机空中碰撞概率模型
2.1 坐标系的定义及转换
在计算两架多旋翼无人机的空中碰撞概率时, 需要提前获取无人机的位置信息、速度信息以及位置误差信息。然而, 这些数据通常并不处于同一个参考系下, 无法对其进行统一的量化计算, 因此需要将这些数据转换到同一坐标参考系下。在无人机运动学中, 通常有两种常用的坐标系: 机体坐标系和全局坐标系。
(1) 机体坐标系
机体坐标系是始终固定在无人机机体上的一种坐标系, 坐标系符合右手定则, 其原点O位于无人机的重心处, x轴与无人机纵轴保持一致, 指向无人机机头前进的方向; y轴垂直于无人机对称面且指向机身左侧; z轴处于无人机对称面内, 方向通过x轴、y轴由右手定则确定。
(2) 全局坐标系
全局坐标系是相对于地球表面静止不动的坐标系, 符合右手定则, 其原点O位于地面上的某一点, y轴指向正北方向, z轴垂直于地面并指向地心, x轴位于水平面内, 方向通过y轴、z轴由右手定则确定, 机体坐标系到全局坐标系的坐标转换矩阵P的计算如下:
式中: θ为无人机航向; φ为无人机爬升角。
2.2 无人机瞬时碰撞概率
设
对于无人机在机体坐标系中的位置误差, 为了便于理论分析, 本文假设无人机位置误差在3个方向上相互独立, 因此在计算碰撞概率时, 每架无人机的位置误差都是独立同分布的。根据中心极限定理,
式中: Λ为对角矩阵。
设目标无人机和入侵无人机的位置向量分别为rM和rH, 速度向量分别为vM和vH, 则两架无人机的相对位置向量Δ re和相对速度向量Δ ve可以分别表示为
式中:
假设两架无人机的飞行轨迹相互独立且均服从高斯分布, 则由高斯分布的性质可知, 其相对位置向量Δ re也服从高斯分布, 即
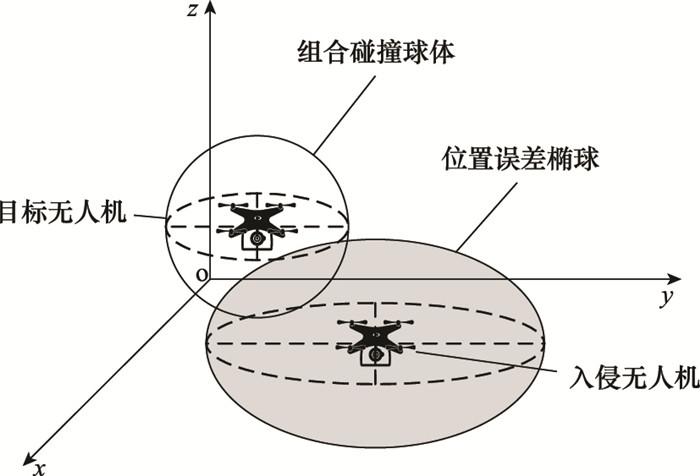
根据以上定义, 令目标无人机带有两架无人机的组合碰撞保护区, 入侵无人机带有两架无人机的组合位置误差椭球(三维高斯分布的等概率曲面为椭球), 则无人机的碰撞概率可以视为一个服从三维高斯分布的概率密度函数在目标无人机组合碰撞保护区域内的积分, 如图 4所示。
图4
图4
无人机碰撞概率示意图
Fig.4
Schematic diagram of unmanned aerial vehicle collision probability
令
用D表示两架无人机的组合碰撞区域, 则
式中: p用于表示处于无人机组合碰撞球体内的三维空间向量。此时, 目标无人机和入侵无人机在当前时刻的瞬时碰撞概率PC可表示为
因此, 无人机的瞬时碰撞概率可以在计算机中利用数值积分的方法得到具体的计算结果。
2.3 无人机最大碰撞概率
无人机的瞬时碰撞概率表示了无人机在当前时刻与其他无人机发生碰撞的可能性。然而, 无人机空中相遇是一个持续的过程, 在两架无人机相互接近的过程中, 每一时刻的碰撞概率都是在动态变化的, 当前时刻的碰撞概率不能反映整个相遇过程的危险程度。因此, 在进行无人机安全间隔标定时, 需计算无人机在相遇过程中的最大碰撞概率。
设当前时刻为t0, 两架无人机的初始位置向量分别为ra和rb, 初始速度向量分别为va和vb, 则两机的相对位置向量和相对速度向量可以分别表示为
此时无人机的速度与位置关系如图 5所示。
图5
图5
目标无人机与入侵无人机相遇时的速度与位置关系
Fig.5
Velocity and position relationship when the target unmanned aerial vehicle and the invading unmanned aerial vehicle meets
由于两架无人机在空中的相遇时间较短, 在相遇过程中的速度可视为不变, 因此在t时刻两架无人机的位置向量可以分别表示为
此时两机的相对位置向量为
令ρ(t)= r2(t), 用于度量两架无人机之间的相对距离, 对ρ(t)进行求导并令其导函数为零, 可得
设tcpa为两机到达相遇最近点(closest point of approach, CPA)处的时刻, 此时两架无人机之间的相对距离最小, ρ(t) 取到最小值, 因此可根据式(15)求出两机到达CPA处的时间:
于是, 两机在CPA处的相对距离为
根据式(17)可以计算出两架无人机在相遇过程中的最短相对距离, 在到达CPA点时, 两机的相对距离最小, 对应的瞬时碰撞概率最大, 因此可以根据式(10)计算出两机在CPA处的瞬时碰撞概率, 并将此时的碰撞概率作为无人机相遇过程中的最大碰撞概率。
3 无人机安全间隔标定模型
3.1 自由空域
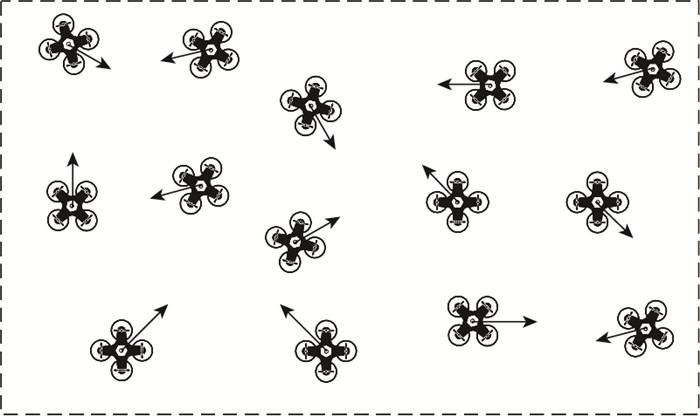
在低空交通领域, 由于目前世界各国尚处于低空发展的起步阶段, 因此低空空域的范围及类型划分均没有明确定义, 大多数无人机在低空空域中的活动以自由飞行为主, 没有预先划设的航路/航线, 可以将无人机视作在自由空域中飞行。在自由空域中, 如图 6所示, 无人机在飞行时受到的约束较少, 可以选择点对点的方式飞行。因此, 无人机通常会表现出一种较为随机的飞行状态。在该状态下, 无人机未来时刻的航向信息、位置误差信息与当前时刻关联较小, 可以将其视为一种布朗运动, 每一时刻的状态由不确定因素所决定。为满足研究需要, 本文假设无人机在自由空域中的航向角和垂直速度服从均匀分布, 位置误差服从三维高斯分布。
图6
3.2 基于碰撞概率的安全间隔
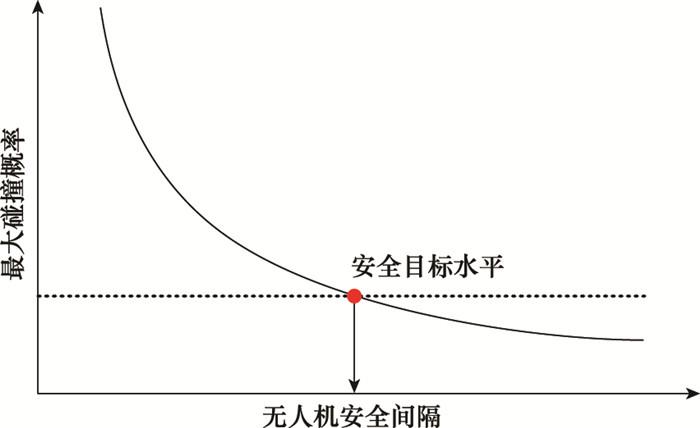
无人机安全间隔是指为防止无人机与无人机空中相撞而设立的一种飞行间隔标准, 当两架无人机的相对距离大于其安全间隔时, 间隔标准的设立可以保证无人机的碰撞风险很小, 并使其达到所要求的安全目标水平。因此, 两架无人机之间的安全间隔与其产生的碰撞风险有着密切的联系。为简化起见, 本文忽略无人机发生碰撞坠落后对于地面人员或建筑产生的影响, 仅将无人机的空中碰撞概率作为衡量碰撞风险的指标。通常, 当两架无人机处于一定的安全间隔标准下时, 可以将其产生的空中碰撞风险量化, 然后将量化后的数值与一个安全目标水平(target level of safety, TLS)进行比较, 以便于确定两架无人机在此安全间隔标准下的飞行是否满足可接受的安全目标水平。因此, 不同的无人机安全间隔可以对应不同的安全目标水平(碰撞概率), 碰撞概率与安全间隔之间存在一一对应的关系[25]。如图 7所示, 在给定一个能够被接受的碰撞概率阈值时, 就能够根据这种映射关系反推出无人机的安全间隔。
图7
图7
基于碰撞概率的安全间隔示意图
Fig.7
Schematic diagram of safety separation based on collision probability
3.3 无人机安全间隔标定方法
以目标无人机重心为坐标原点, 正北方向为y轴, 地面的垂直方向为z轴, 建立空间直角坐标系, 构建一个大小为xmax×ymax×zmax的三维空间。假设目标无人机以大小为vMh的水平速度朝正北方向飞行, 根据本文建立的无人机空中碰撞概率模型, 在给定无人机的相对位置信息、相对速度信息和相对位置误差信息时, 可以计算出两架无人机的最大碰撞概率。因此, 可以依次枚举入侵无人机在该三维空间中所有可能出现的位置, 计算出不同位置下的最大碰撞概率, 然后将相同碰撞概率的坐标点相连, 即可得到关于最大碰撞概率的等值面。在给定安全目标水平(可接受的最大碰撞概率)时, 取等值面在纵向、横向和垂直3个方向的最大值, 即可确定无人机的安全间隔。
对于每一次枚举而言, 入侵无人机的位置信息和位置误差信息都是确定的, 因此只需要确定入侵无人机的相对速度信息, 即可计算出最大碰撞概率。设入侵无人机的水平速度大小为vHh, 航向角为θ, 垂直速度大小为vHz, 则两机的相对速度向量vr可表示为
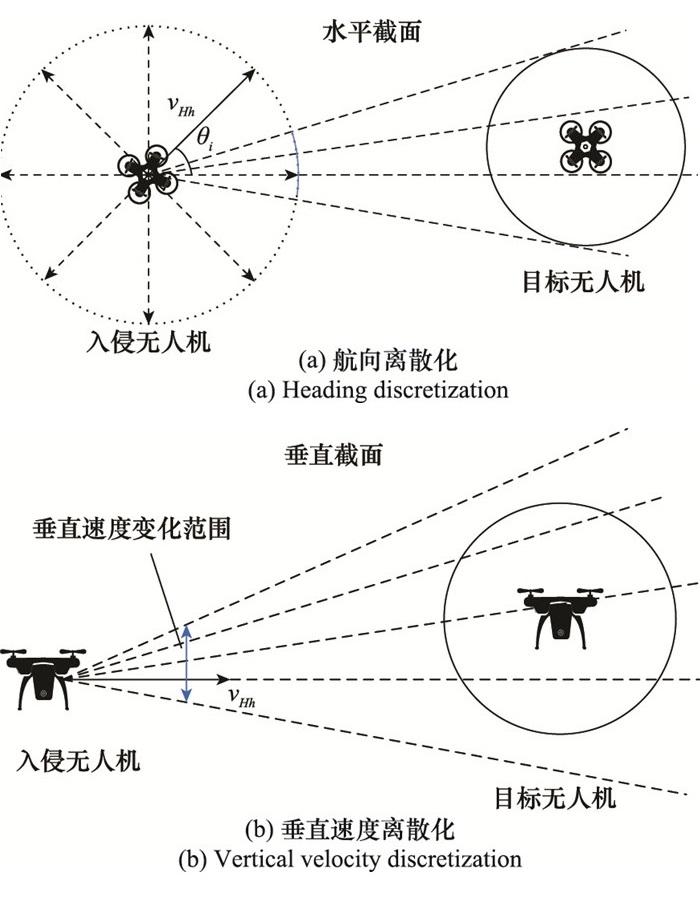
根据第3.1节的模型假设, 自由空域下无人机的航向角θ、垂直速度大小vz服从均匀分布, 因此可对式(18)中的θ和vHz进行离散化处理。如图 8所示, 针对每一次碰撞概率计算, 将入侵无人机的航向角在[0, 2π)范围内等分为n个离散航向角θi(i=1, 2, …, n), 将垂直速度在[vHzmin, vHzmax]范围内等分为m个离散垂直速度vj(j=1, 2, …, m), vHzmin, vHzmax分别为无人机的最大下降速度和最大上升速度。
图8
图8
航向与垂直速度离散化示意图
Fig.8
Schematic diagram of the discretization of heading and >vertical velocity
此时, 两机在给定相对位置下的最大碰撞概率可以表示为
式中: P(C)表示在给定相对位置下两架无人机的最大碰撞概率, 由于入侵无人机的航向角θ、垂直速度vz均被离散化表示, 因此碰撞事件C被均匀分解为了n×m个子事件, 每个碰撞子事件用Hij表示, Hij发生的概率P(Hij)可以使用第2节提出的方法计算。
需要注意的是, 多旋翼无人机在飞行过程中一般会存在最大俯仰角度限制, 为了保证安全间隔标定结果的准确性, 在离散化无人机的垂直速度时需要考虑该约束条件的限制。设无人机最大俯仰角度为φmax, 当前离散垂直速度为vj(j=1, 2, …, m), 则需要满足
式中: vHh为无人机水平速度大小。
因此, 给定目标无人机与入侵无人机的巡航速度vMh, vHh, 位置误差矩阵ΛM, ΛH, 碰撞盒半径RM, RH, 入侵无人机的最大下降速度和最大上升速度vHzmin, vHzmax, 根据本节所提出的无人机安全间隔标定方法, 即可确定两架无人机在3个方向上的安全间隔。
4 实例分析
由于不同机型无人机的相关技术参数不同, 导致其所对应的安全间隔也不同, 为了验证本文所提出的自由空域下多旋翼无人机安全间隔标定方法的有效性, 本节将以经纬M600 Pro型无人机为研究对象, 分析其在自由空域中的安全间隔。经纬M600 Pro无人机的相关技术参数如表 1所示。
表1 经纬M600 Pro无人机相关技术参数
Table 1
| 技术参数 | 数值 |
| 外形尺寸(长×宽×高) | 1 668 mm×1 518 mm×759 mm |
| 悬停精度(GPS精度) | 垂直: ±0.5 m, 水平: ±1.5 m |
| 最大俯仰角度/(°) | 25 |
| 最大上升速度/(m/s) | 5 |
| 最大下降速度/(m/s) | 3 |
| 最大水平飞行速度/(km/h) | 65(无风环境) |
图9
图10
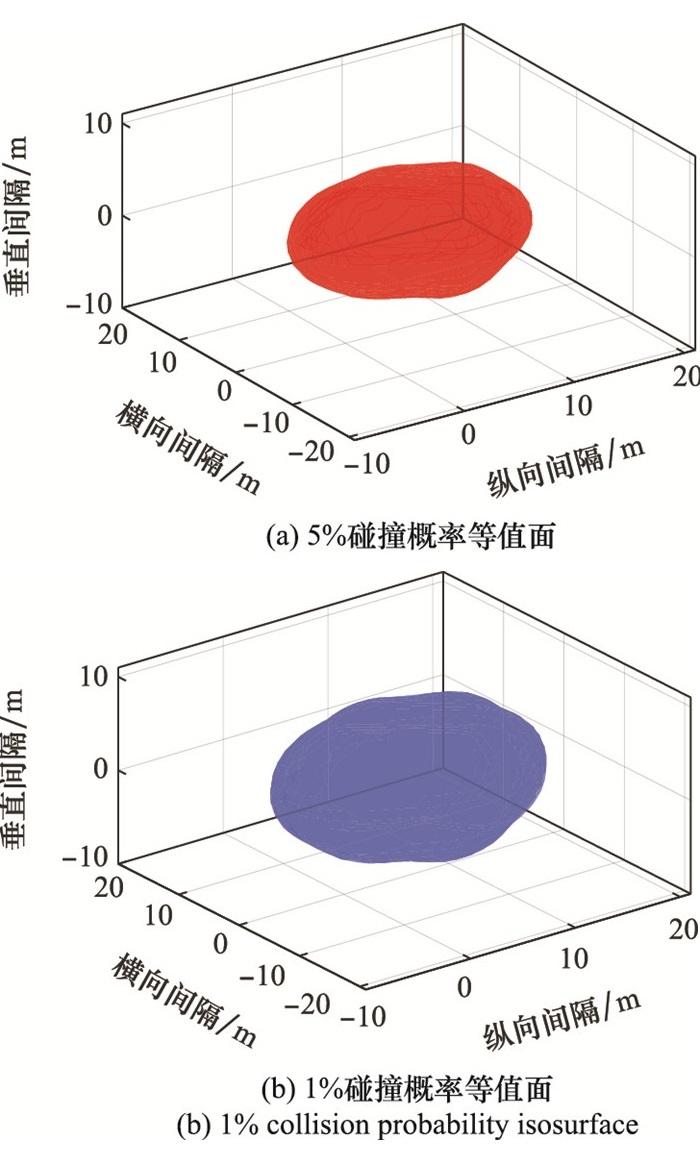
图10
无人机碰撞概率等值面
Fig.10
Collision probability isosurface of unmanned aerial vehicle
图11
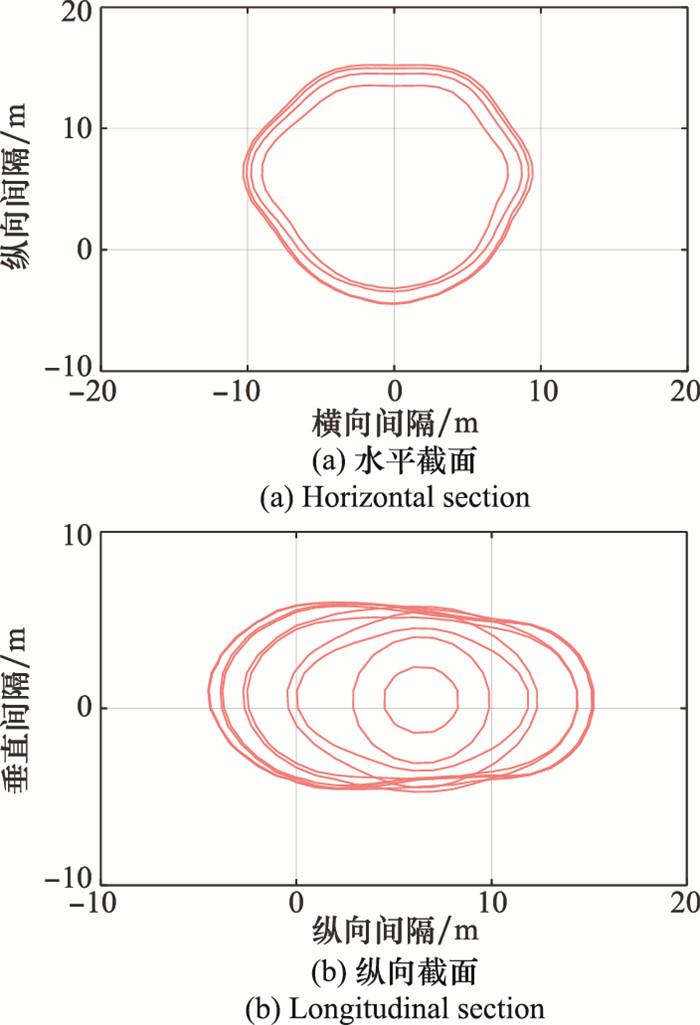
图11
无人机5%碰撞概率等值面截面
Fig.11
5% collision probability isosurface section of unmanned aerial vehicle
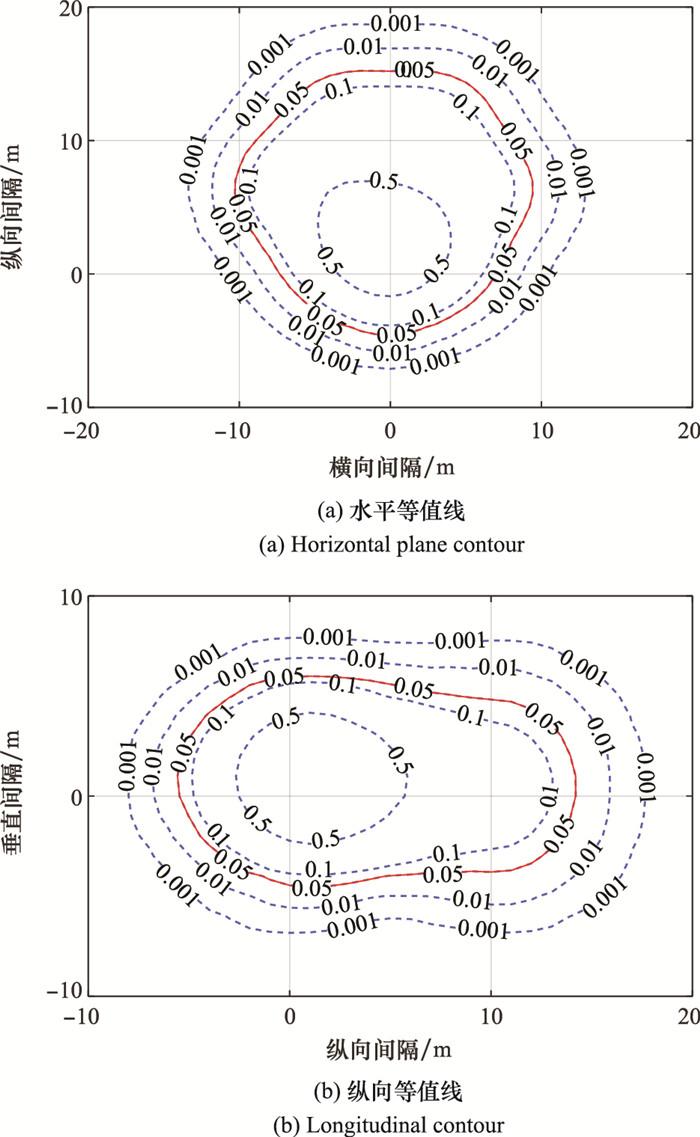
在图 9(a)中, 当入侵无人机位于目标无人机后方时, 从式(18)可以看出, 此时两架无人机之间的相对速度较小, 因此计算得到的碰撞概率较小, 在图中表现为相同碰撞概率等值线距离原点较近; 反之, 当入侵无人机位于目标无人机前方时, 两机的相对速度较大, 因此计算得到的碰撞概率较大, 等值线距离原点较远。从中可以得出结论: 当入侵无人机位于目标无人机后方时, 两机的安全间隔较小; 当入侵无人机位于目标无人机前方时, 两机的安全间隔较大。即目标无人机的前向间隔大于后向间隔。在图 9(b)中, 当入侵无人机位于目标无人机正上方或正下方时, 对应的碰撞概率最大, 此时等值线距离原点较远。同时, 由于目标无人机沿着水平方向飞行, 俯仰角为0°, 且入侵无人机的垂直速度被均匀地离散化处理, 因此碰撞概率等值线在图中表现为沿水平方向对称。图 10和图 11将二维空间拓展至三维空间, 分别描绘了两机5%和1%碰撞概率等值面以及等值面的截面。从图中可以看出, 1%碰撞概率等值面的覆盖范围相较于5%碰撞概率等值面的覆盖范围更广, 结果是符合预期的, 这是因为当入侵无人机的位置相对于目标无人机越远时, 对应的碰撞概率越小, 因此1%碰撞概率等值面的面积较大。
从以上分析可以看出, 无人机安全间隔分别与两架无人机的飞行速度大小有关。然而, 当无人机在自由空域中飞行时, 飞行速度大小通常是在不断变化的, 因此在进行安全间隔标定时需要考虑所有相对速度情况下的安全间隔。本文假设在自由空域中,所有无人机的巡航速度vh均在其对应机型最大水平飞行速度的30%~70%内, 即
式中: vhmax为无人机最大水平飞行速度。
仍然以M600 Pro无人机为例, 该型无人机的巡航速度区间为(5.4 m/s~12.6 m/s)。本文以1 m/s为速度搜索步长, 依次计算目标无人机和入侵无人机处于不同巡航速度下的安全间隔, 计算结果如图 12所示。
图12
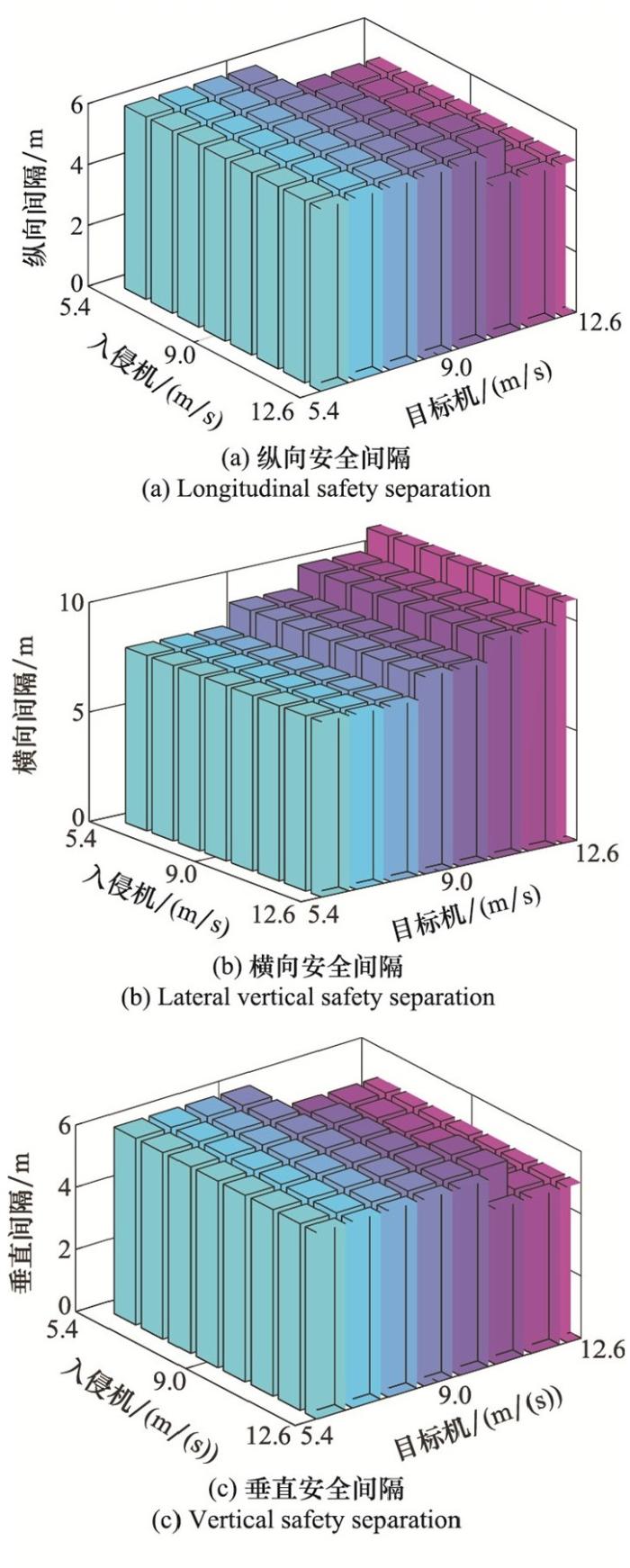
图12
不同巡航速度下的安全间隔标定结果
Fig.12
Demarcation result of safety separation at different cruising speeds
根据目标无人机和入侵无人机处于不同巡航速度下的安全间隔标定结果, 分别取3个方向中每种情况的最大值, 由此得到在自由空域下, 两架M600 Pro无人机之间的纵向、横向和垂直安全间隔, 其值分别为: 16 m, 11 m和6 m。
5 结论
本文主要面向自由空域, 提出了一种基于碰撞概率的无人机与无人机之间安全间隔标定方法。以经纬M600 Pro无人机为例, 应用本文方法, 分析了其在自由空域下最大碰撞概率的变化曲线。通过将相同碰撞概率的坐标点相连, 形成关于最大碰撞概率的等值线和等值面。当安全目标水平取为5%碰撞概率时, 最终得出两架M600 Pro无人机的纵向、横向和垂直间隔分别为16 m、11 m、6 m。实例分析结果表明, 本文方法适用于小型多旋翼无人机, 具备较强的可实施性。同时, 伴随着自动驾驶技术的发展, 未来智慧城市环境中会出现大量民用无人机自主运行的情况, 亟需针对民用无人机制定一套合理的安全间隔标准。因此, 应用本文方法标定安全间隔, 可以有效保障未来民用无人机在城市低空航路上的安全、高效运行。
参考文献
无人机低空交通管理系统综述
[J].
Overview of low altitude air traffic management system for UAS
[J].
Analysis of long-range air traffic systems: separation standards-Ⅰ
[J].DOI:10.1017/S037346330004056X [本文引用: 1]
Analysis of long-range air traffic systems: separation standards—Ⅲ
[J].
Analysis of long-range air traffic systems: separation standards—Ⅱ
[J].DOI:10.1017/S0373463300047196 [本文引用: 1]
Aircraft collision risk in the North Atlantic region
[J].DOI:10.1057/jors.1984.145 [本文引用: 1]
European studies to investigate the feasibility of using 1 000 ft vertical separation minima above FL 290 Part Ⅰ
[J].
European studies to investigate the feasibility of using 1 000 ft vertical separation minima above FL 290. Part Ⅱ: precision radar data analysis and collision risk assessment
[J].
European studies to investigate the feasibility of using 1 000 ft vertical separation minima above FL 290. Part Ⅲ: further results and overall conclusions
[J].
A collision risk model for a crossin track separation methodology
[J].DOI:10.1017/S0373463300013576 [本文引用: 1]
基于布朗运动的自由飞行下碰撞风险研究
[J].
Study on free flight collision risk based on Brownian motion
[J].
自由飞行下基于贝叶斯网络的碰撞风险研究
[J].
Bayesian network-based study on collision risk in free flight
[J].
自由飞行下基于冲突解脱的碰撞风险模型研究
[J].
Study on free flight collision risk model based on conflict resolution
[J].
自由飞行下基于航空器定位误差修正的碰撞风险研究
[J].
On the collision risk in rectification of the aircraft positioning error under the free flight condition
[J].
Fast collision detection for small unmanned aircraft systems in urban airspace
[J].
Probabilistic safety assessment of unmanned aerial system operations
[J].
无人机与民航客机碰撞概率研究
[J].
Research of collision probability of unmanned aerial vehicals and civil airplane
[J].
Well-clear re-commendation for small unmanned aircraft systems based on unmitigated collision risk
[J].