系统工程与电子技术, 2023, 46(1): 113-120 doi: 10.12305/j.issn.1001-506X.2024.01.13

传感器与信号处理

基于杂波拖尾分布的雷达无人机检测性能分析

杨勇, 王雪松

国防科技大学电子信息系统复杂电磁环境效应国家重点实验室, 湖南 长沙 410073

Analysis of radar detection performance for UAV based on clutter tail distribution

YANG Yong, WANG Xuesong

State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System, National University of Defense Technology, Changsha 410073, China

通讯作者: 杨勇

收稿日期: 2022-07-11  

基金资助: 国家自然科学基金.  62171447
国家自然科学基金.  61971429
国家自然科学基金.  61871385

Received: 2022-07-11  

作者简介 About authors

杨勇(1985—),男,教授,博士,主要研究方向为雷达低空目标检测 。

王雪松(1972—),男,教授,博士,主要研究方向为极化雷达信号处理、雷达精确制导 。

摘要

固定翼无人机(unmanned aerial vehicle, UAV)给雷达低空监视提出了严峻挑战。分析雷达对固定翼UAV的检测性能, 可为雷达UAV检测能力评估和技术升级提供重要参考。本文结合雷达探测低空固定翼UAV外场实测数据, 首先分析了低空固定翼UAV雷达接收信号幅度统计分布, 采用多项式对杂波拖尾导致的虚警概率进行拟合建模; 然后, 根据虚警概率分布得到雷达检测门限; 进而根据UAV回波+杂波幅度分布理论推导得到雷达检测概率; 最后, 将理论分析性能与传统性能分析结果、雷达实际检测性能进行对比。结果表明, 采用多项式对杂波拖尾导致的虚警概率进行单独建模, 由此获得的雷达检测门限精度更高, 从而使雷达UAV检测性能分析结果较传统性能分析结果更准确。

关键词： 雷达检测 ; 杂波拖尾 ; 无人机 ; 性能分析 ; 虚警概率

Abstract

Detection of the fixed-wing unmanned aerial vehicle (UAV) is an important issue for low-altitude radar surveillance. Analyzing the radar detection performance for fixed-wing UAV provides important reference for the evaluation and technical upgrade of radar UAV detection capability. In this paper, based on the experimental data of radar detection of low-altitude fixed-wing UAV, the statistical distribution of fixed-wing UAV radar received signal amplitude is analyzed at first. Then the false alarm probability caused by the clutter tail is modeled by polynomial. Then, according to the distribution of the tail of false alarm probability and the distribution of amplitude of UAV echo plus clutter, the detection threshold and radar detection performance are obtained by theoretical derivation. Finally, the theoretical radar detection performance is compared with traditional performance analysis results and actual radar detection performance. The comparison results show that radar detection threshold owns higher accuracy by using the polynomial to fit the tail of the false alarm probability, which makes the prediction of radar UAV detection performance has higher accuracy than the traditional methods.

Keywords： radar detection ; clutter tail ; unmanned aerial vehicle (UAV) ; performance analysis ; false alarm probability

PDF (2162KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

杨勇, 王雪松. 基于杂波拖尾分布的雷达无人机检测性能分析. 系统工程与电子技术[J], 2023, 46(1): 113-120 doi:10.12305/j.issn.1001-506X.2024.01.13

YANG Yong. Analysis of radar detection performance for UAV based on clutter tail distribution. Systems Engineering and Electronics[J], 2023, 46(1): 113-120 doi:10.12305/j.issn.1001-506X.2024.01.13

0 引言

固定翼无人机现已广泛应用于军事侦察、目标精确打击等领域[1-3]。固定翼无人机雷达截面积较小、飞行高度较低、速度较慢, 无人机回波被强杂波淹没, 导致雷达难以及时检测到无人机[4-7]。现有低空监视雷达对固定翼无人机的检测性能到底怎样？这是低空监视雷达作战效能评估和技术升级必须回答的问题。所以, 准确分析雷达对固定翼无人机的检测性能, 是低空监视雷达系统设计、研制和作战使用的基础, 具有重要意义。

目前, 关于雷达无人机检测性能分析的公开文献较少, 但关于雷达目标检测性能分析的公开文献较多。鉴于外场试验耗费高、代价大、试验难以重复等问题, 国内外通常采用理论分析与仿真实验或者实测数据处理相结合的方式分析雷达目标检测性能[8-15]。这方面的研究工作主要分为两类: 一是采用经验模型对雷达接收信号进行统计建模, 然后理论推导得到雷达目标检测性能[8-10]; 二是结合实测数据对雷达接收信号统计分布进行拟合, 然后根据拟合模型分析雷达目标检测性能[11-13]。对于这两类分析方法, 雷达目标检测性能分析结果均与雷达接收信号模型息息相关[16-18]。因此, 杂波分布模型和杂波+目标回波分布模型的精确度直接决定了雷达目标检测性能分析结果的精度。其中, 杂波分布模型的精确度决定了雷达检测门限的精度, 进而影响雷达目标检测性能分析结果的精度, 所以杂波分布建模至关重要。

目前, 国内外学者对杂波分布进行建模时, 主要对杂波幅度全部取值的统计分布进行拟合建模[19-23]。这种建模思路从数学层面讲, 科学严谨, 但从工程角度看, 在低虚警概率条件下适用性不强。因为在实际中, 雷达虚警概率需控制在较低的恒定的水平, 此时雷达检测门限只需根据杂波拖尾分布来获取, 而与杂波全部取值分布关系不大。为了获取高精度的检测门限, 须对杂波拖尾分布进行单独建模, 或者对杂波拖尾导致的虚警概率分布进行单独建模。

本文结合雷达探测固定翼无人机外场实测数据, 对雷达杂波拖尾导致的虚警概率分布进行建模, 在此基础上插值获得雷达检测门限。然后, 再根据实测杂波+无人机回波幅度分布, 理论推导得到雷达无人机检测性能。本文结合实测数据将基于杂波拖尾的雷达无人机检测性能分析结果与传统性能分析结果(先根据杂波幅度全部取值的统计分布获取检测门限, 再根据实测杂波与无人机回波叠加信号的幅度分布, 推导雷达无人机检测性能)进行对比, 结果表明, 基于杂波拖尾的雷达无人机检测性能分析结果精度显著提高。

1 雷达回波幅度分布

雷达接收信号x可表示为

式中: H0、H1分别表示无人机不存在和存在; s和c分别表示无人机回波和杂波。

实际雷达系统通常采用接收信号的幅度或者功率作为检验统计量来判断目标是否存在。不失一般性, 本文采用雷达接收信号幅度作为检验统计量。令z=|x|, 则雷达虚警概率Pf和检测概率Pd[24]分别可表示为

$P_f=\int_\eta^{\infty} f\left(z \mid \mathrm{H}_0\right) \mathrm{d} z$

$P_d=\int_\eta^{\infty} f\left(z \mid \mathrm{H}_1\right) \mathrm{d} z$

式中: f(z|H0)和f(z|H1)分别表示H0和H1条件下雷达接收信号幅度的概率密度函数; η为检测门限。在虚警概率恒定的情况下, 为了计算检测门限, 需先获得f(z|H0)。在获得检测门限和f(z|H1)后, 即可计算雷达对无人机的检测概率。下面结合雷达探测无人机外场实测数据分析杂波、无人机回波+杂波的幅度分布特性。

1.1 杂波幅度分布

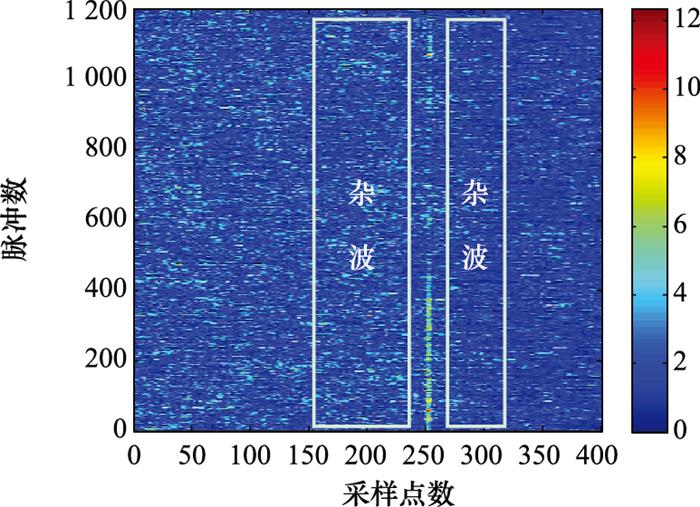
杂波幅度分布与雷达工作参数、环境参数息息相关。不同场景下雷达杂波幅度分布通常不同。常用于描述杂波幅度分布的函数有: 瑞利分布、韦布尔分布、对数正态分布、K分布、伽马分布等[25-26]。下面采用这些函数对雷达实测杂波幅度分布进行拟合建模。

本文采用的杂波实测数据为某雷达开展无人机外场探测试验时录取的杂波数据, 试验场景详见文献[7]。雷达工作中心频率为9.4 GHz, 发射信号为线性调频信号, 带宽为5 MHz, 脉冲重复周期为1.25 ms, 采样率为10 MHz, 极化方式为HH极化。雷达实测回波数据经过脉冲压缩之后的回波幅度如图 1所示。该数据为一个1 200×400的数组, 其中1 200表示脉冲数, 400表示距离向采样点数, 每个采样点对应的距离为15 m，无人机目标位于第250~255个距离向采样点。本文选取第101~240、261~320列的数据来统计杂波幅度分布, 选取杂波数据组成一个1 200×200矩阵, 杂波样本数据共240 000个。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   雷达探测无人机脉压输出信号幅度

Fig.1   Radar detection of unmanned aerial vehicle pulse compression output signal amplitude


在用经典分布对杂波幅度分布进行拟合之前, 首先需根据实测数据估计各经典分布的关键参数, 各经典分布概率密度函数及其关键参数估计方法如表 1所示。其中, 关键参数估计主要采用矩估计方法[27], m(1)、m(2)分别表示一、二阶矩, interp表示插值运算, 其功能与仿真软件中的interp1函数功能一样, Γ(·)表示Gamma函数[28], 表达式为$ \varGamma(z)=\int_0^{\infty} u^{z-1} \mathrm{e}^{-u} \mathrm{~d} u, K_{\varsigma_{-1}}$(·)表示$\varsigma^{-1} $阶第二类修正Bessel函数[28], 表达式为$K_v(z)=\frac{\pi}{2 \sin v \pi}\left[I_{-v}(z)-\right.\left.I_v(z)\right] $, 其中$I_v(z)=\sum\limits_{m=0}^{\infty} \frac{1}{m ! \varGamma(v+m+1)}\left(\frac{z}{2}\right)^{2 m+v} $。

表1   各种经典分布概率密度函数及其关键参数估计方法

Table 1  Various classical distribution probability density functions and the corresponding estimation methods for their key parameters

分布概率密度函数关键参数估计
瑞利分布$ f(x)=\frac{x}{\sigma^2} \mathrm{e}^{-\frac{x^2}{2 \sigma^2}}$$ \hat{\sigma}^2=\frac{1}{2} m(2)$
对数正态分布$f(x)=\frac{1}{\sqrt{2 \pi \alpha^2 x^2}} \mathrm{e}^{-\frac{(\ln x-\ln \mu)^2}{2 \alpha^2}} $$\hat{\alpha}^2=\ln \left[m(2) / m^2(1)\right], \mu=m(1) / \mathrm{e}^{\hat{\sigma}^2 / 2} $
韦布尔分布$f(x)=\frac{c}{b^c} x^{c-1} e^{-}\left(\frac{x}{b}\right)^{c} $$\hat{c}=\operatorname{interp}\left[\varOmega, c, m(2) / m^2(1)\right], \hat{b}=\frac{m(1)}{\varGamma\left(\frac{1}{\hat{c}}+1\right)} $
伽马分布$ f(x)=\frac{x^{\gamma-1}}{\varGamma(\gamma) \beta^\gamma} \mathrm{e}^{-\frac{x}{\beta}}$$ \hat{\beta}=\frac{m(2)-m^2(1)}{m(1)}, \hat{\gamma}=\frac{m(1)}{\hat{\beta}}$
K分布$f(x)=\frac{2}{\chi \varGamma(\varsigma)}\left(\frac{x}{2 \chi}\right)^{\varsigma} K_{\varsigma-1}\left(\frac{x}{\chi}\right) $$ \begin{array}{l}\;\;\;\;\;\;\;\varsigma=\operatorname{interp}\left(x_0, y_0, x_d\right), \chi=\sqrt{\frac{m(2)}{4 \zeta^2}} \\y_0=[0.1, 100], x_0=\frac{\varGamma\left(y_0+1\right) \varGamma\left(y_0\right)}{\varGamma^2\left(y_0+\frac{1}{2}\right) \varGamma^2\left(\frac{3}{2}\right)}\end{array}$

新窗口打开| 下载CSV


在估计得到各分布关键参数后, 采用KS(Kolmogorov-Smirnov)检验方法对各种分布函数的拟合效果进行评估[29-30]。值得一提的是, KS检验时, 拟合效果不仅与分布函数有关, 还与杂波幅度取值区间的分段数有关, 分段数越多, 杂波幅度分布刻画越精细, 但对其进行准确拟合的难度越大。在此, 令杂波取值区间分段数分别为50、100、500, 得到各种分布函数对实测杂波幅度的拟合效果如图 2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   雷达杂波幅度分布拟合结果

Fig.2   Fitting results of radar clutter amplitude distribution


通过KS检验得到的拟合结果如表 2所示。其中, 拟合度是指实测数据分布与假定的分布函数之间的匹配程度, 用P值表示[30], P值越大, 假定的分布函数与实测数据分布的拟合效果越好。最大拟合误差为

$\Delta F=\max \left[\left|F_r(x)-F_f(x)\right|\right]$

表2   杂波幅度分布拟合效果

Table 2  Fitting effects of clutter amplitude distribution

分布N=50N=100N=500
拟合度最大拟合误差拟合度最大拟合误差拟合度最大拟合误差
瑞利分布0.510.160.340.133e-70.18
对数正态分布0.240.20.020.211e-100.22
韦布尔分布0.990.060.790.093e-70.18
伽马分布0.680.140.340.133e-70.18
K分布0.950.10.790.093e-70.18

新窗口打开| 下载CSV


式中: Fr(x)和Ff(x)分别表示实际数据和拟合分布的累积分布函数。

结合图 1和表 2可见, 当杂波取值区间分段数小于100时, 韦布尔分布与实测数据统计分布拟合效果最好, K分布拟合效果其次。当杂波取值区间分段数为500时, 各分布拟合效果均较差, 这是由于拖尾部分各种经典分布拟合效果均较差所致。下文在采用传统杂波幅度分布建模方法分析雷达检测性能分析时, 杂波幅度分布将建模为韦布尔分布。

1.2 无人机回波+杂波幅度分布

无人机回波位于图 1中第251~255列, 为此, 选取这5列数据来分析无人机回波+杂波幅度分布, 分析方法与第2.1节类似。各种经典分布函数的拟合结果如图 3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   无人机回波+杂波幅度分布拟合结果

Fig.3   Fitting results of unmanned aerial vehicle echo plus clutter amplitude distribution


同样, 采用KS检验对各种经典分布的拟合效果进行检验, 信号幅度取值区间分段数分别为50、100、500, KS检验结果如表 3所示。

表3   无人机回波+杂波幅度分布拟合结果

Table 3  Fitness result of unmanned aerial vehicle echo plus clutter amplitude distribution

分布N=50N=100N=500
拟合度最大拟合误差拟合度最大拟合误差拟合度最大拟合误差
瑞利分布0.680.140.140.165.4e-140.25
对数正态分布0.840.120.140.165.4e-140.25
韦布尔分布0.990.080.680.15.4e-140.25
伽马分布0.950.10.560.115.4e-140.25
K分布0.990.080.680.15.4e-140.25

新窗口打开| 下载CSV


结合图 3和表 3可以看到, 当信号幅度取值区间分段数小于100时, 韦布尔分布、K分布对无人机回波+杂波幅度分布拟合效果最好, 且二者效果相当。当信号幅度取值区间分段数为500时, 各种分布拟合效果均较差, 因为拖尾部分的拟合效果均较差。下文分析雷达检测性能时, 为了推导方便, 将无人机回波+杂波幅度分布建模为韦布尔分布。

在此特别强调, 由图 2和图 3可见, 在对实测数据拟合时, 取值分段数越多, 实测数据拖尾部分的拟合效果越差。而对于实际雷达系统, 为了使虚警率保持在较低的水平, 主要关注的正是杂波拖尾。因此, 在下文中, 将提出针对杂波拖尾导致的虚警概率进行单独建模, 以保证检测门限具有较高的精度, 进而保证雷达检测性能分析结果的精度。

2 虚警概率拖尾建模

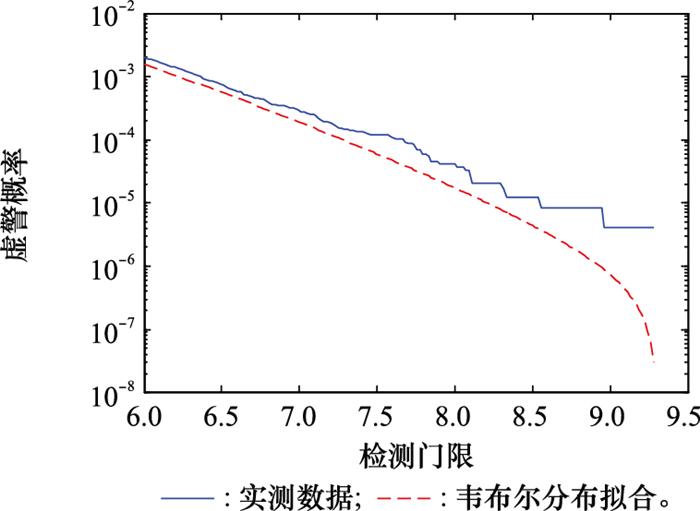
根据第2节的实测杂波数据分析结果, 杂波幅度服从韦布尔分布, 此时雷达虚警概率可表示为

$P_f=\int_\eta^{\infty} \frac{c}{b^c} x^{c-1} \exp \left[-\left(\frac{x}{b}\right)^c\right] \mathrm{d} x=\exp \left[-\left(\frac{\eta}{b}\right)^c\right]$

式中: b为尺度参数, 与杂波功率有关; c为形状参数, 与杂波起伏剧烈程度有关。雷达虚警概率随检测门限的变化曲线如图 4所示。虽然第2.1节分析表明，韦布尔分布对所选择的杂波数据统计分布拟合效果最好, 但从图 4中可以看出, 当虚警概率低于10-3时, 通过式(4)反推得到的检测门限与实际检测门限之间存在误差, 且随着虚警概率的降低, 误差逐渐增大。这是由于韦布尔分布对实测杂波拖尾拟合效果较差导致。在实际中, 雷达系统虚警概率往往要远低于10－3。这种情况下, 基于传统的杂波幅度全部取值分布建模得到检测门限存在较大误差, 这会导致雷达无人机检测性能分析结果产生较大误差。若要提高雷达检测性能分析精度, 需要提高检测门限估计精度, 即需要对杂波拖尾分布(或者图 4中的虚警概率拖尾)进行高精度拟合建模。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   虚警概率随检测门限变化关系

Fig.4   False alarm probability versus detection threshold


结合图 1中选取的实测杂波数据, 对杂波拖尾导致的虚警概率进行拟合。分析发现，表 1中的几种经典分布拟合效果均较差, 而多项式分布能够较好地拟合虚警概率拖尾分布。多项式分布拟合结果如图 5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

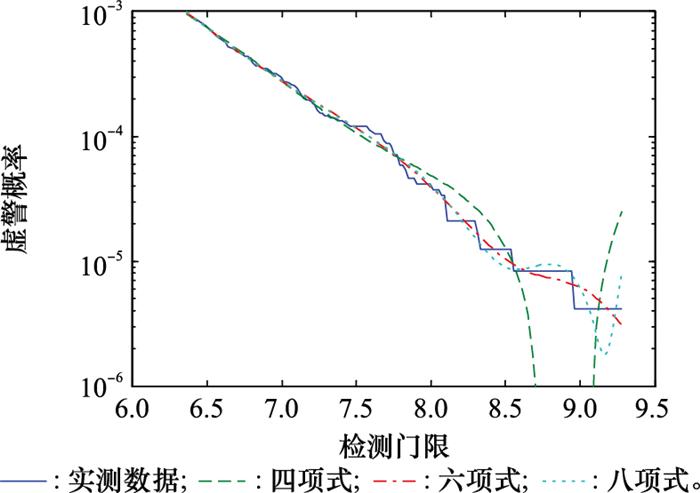
图5   雷达虚警概率多项式拟合结果

Fig.5   Polynomial fitting results for radar false alarm probability


拟合时, 采用线性最小均方估计准则对虚警概率拖尾进行多项式拟合, 拟合模型为

$P_f=\sum\limits_{n=0}^N a_n z^n$

式中: N为多项式阶数。在拟合过程中, 依次增加多项式阶数。当拟合出的虚警概率为负时, 直接舍去该阶多项式。随着多项式阶数的增加, 计算量逐渐增大, 而拟合改善效果越来越小。为此, 在拟合时, 需权衡计算量和拟合效果, 综合选定多项式阶数。对于所选实测杂波数据, 三项式、四项式、五项式拟合的虚警概率均存在负值情况, 因此不采用; 六项式和八项式拟合效果较好, 二者拟合效果差异甚微, 如图 5所示。采用KS检验对图 5中的四、六、八项式的拟合效果进行检验, 四、六、八项式的拟合度分别为0.02、0.3、0.15, 最大拟合误差分布为0.16、0.1、0.13。可见, 六项式拟合度最高, 且最大拟合误差最小。为此, 选取六项式对虚警概率拖尾进行建模。

3 检测性能分析对比

基于传统的杂波全部幅度取值分布建模方法分析雷达检测性能时, 根据式(4)可得检测门限$\eta=b\left(-\ln P_f\right)^{\frac{1}{c}} $。其中, Pf为设定的虚警概率。实测无人机回波+杂波幅度服从韦布尔分布, 则雷达理论检测概率为

$P_d^w=\int_\eta^{\infty} \frac{c_1}{b_1^{c_1}} x^{c_1-1} \mathrm{e}^{-\left(\frac{x}{b_1}\right)^{c_1}} \mathrm{~d} x=\exp \left[-\left(\frac{\eta}{b_1}\right)^{c_1}\right]$

式中: b1和c1分别为H1假设下韦布尔分布的尺度参数和形状参数。

基于虚警概率多项式拟合方法分析得到的雷达理论检测概率为

$P_d^p=\exp \left[-\left(\frac{\eta_p}{b_1}\right)^{c_1}\right]$

式中: ηp=interp(Pf′, z, Pf), interp表示插值运算, Pf′=$ \sum\nolimits_{n=0}^6 a_6 z^6, P_f^{\prime} \leqslant 10^{-3}$, z为图 5中的横轴取值, Pf为设定的虚警概率。

设ηr为根据实测数据和给定虚警概率得到的实际检测门限, 则雷达实际检测概率为

$P_d^r=\exp \left[-\left(\frac{\eta_r}{b_1}\right)^{c_1}\right]$

对比式(6)~式(8)可知, 3种情况下的检测概率表达式形式一样, 检测门限不一样。图 6给出了基于传统韦布尔分布拟合、基于多项式拟合和实际的雷达无人机检测性能。其中, 根据无人机回波+杂波实测数据估计得到韦布尔分布参数b1=3.39、c1=1.72, 信杂比(signal clutter ratio, SCR)约为4.24 dB。图 6表明, 采用多项式对杂波拖尾导致的虚警概率进行拟合时, 理论检测性能分析结果与实际雷达检测性能分析结果吻合较好, 精度较高。这是因为采用多项式拟合得到的检测门限精度更高。此外, 由于SCR较低, 且雷达虚警概率也较低, 导致图 6中雷达的检测概率较低。

图6

新窗口打开| 下载原图ZIP| 生成PPT

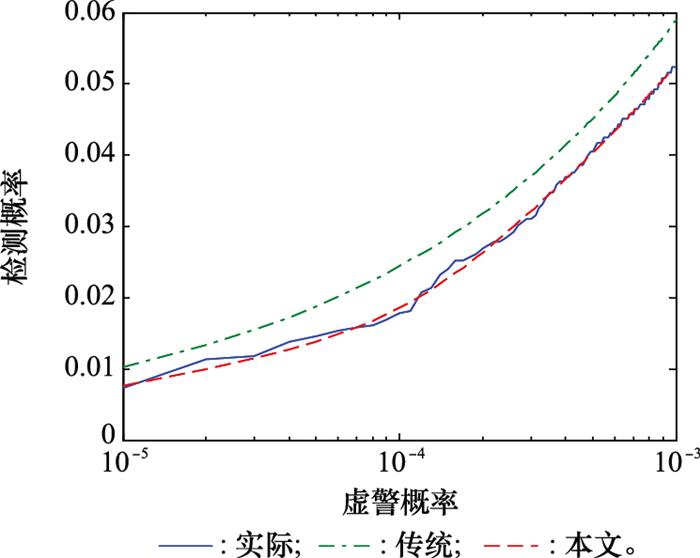
图6   基于实测数据的雷达检测性能对比图

Fig.6   Comparison of radar detection performance with experimental data


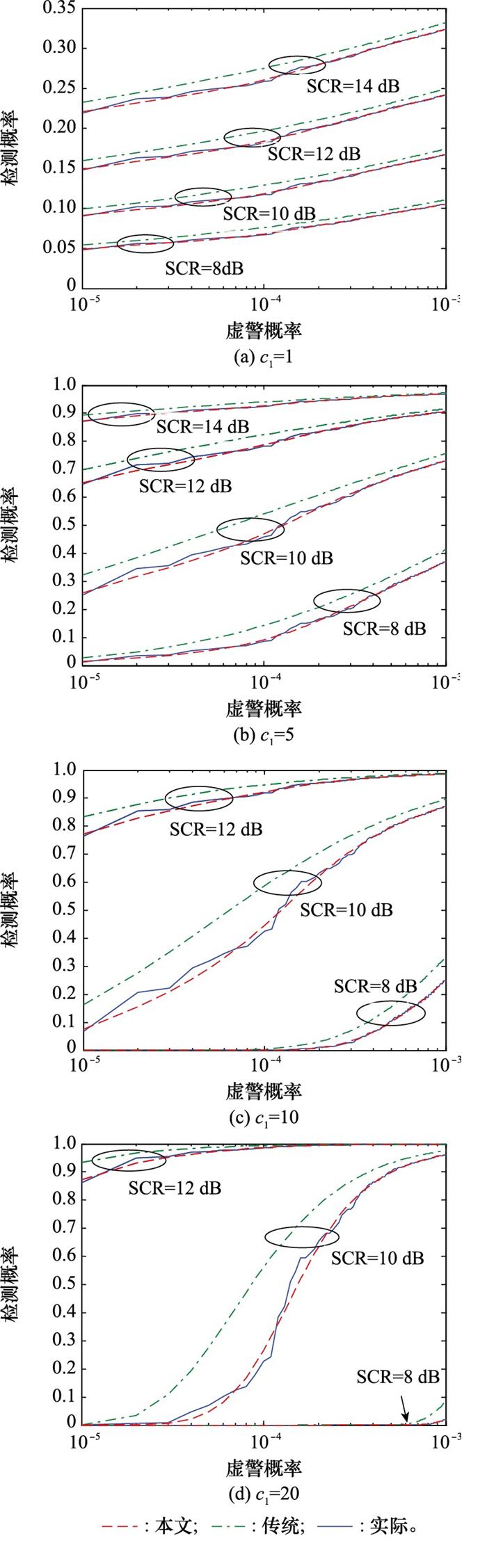
由式(6)~式(8)可见, 雷达检测概率计算精度不仅与门限估计精度有关, 还与b1、c1等参数有关。实际中, 随着无人机与雷达之间距离的变化, SCR会发生改变, b1、c1也会随之改变。为此, 不同c1取值条件下采用3种方法计算得到的雷达检测概率随虚警概率、SCR的变化关系如图 7所示。其中, c1描述了无人机回波+杂波幅度起伏剧烈程度, 在计算检测概率时, c1确定后, b1=$\sqrt{P_x /\left(\varGamma^2\left(1+\frac{2}{c_1}\right)\right)} $, Psc为杂波+目标回波功率。图 7中“传统”“本文”“实际”分别表示根据式(6)~式(8)计算得到的检测性能。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   不同场景下的雷达检测性能

Fig.7   Radar detection performance in various circumstances


图 7表明, 采用多项式拟合杂波拖尾导致的虚警概率时, 分析得到的检测概率误差明显小于传统的杂波幅度分布全段拟合对应的检测概率误差。随着SCR、信号起伏程度的变化, 多项式拟合方法对应的检测概率误差均较小。对于SCR高于12 dB或者低于8 dB的目标, 采用多项式拟合虚警概率拖尾对应的预估误差可忽略。虽然多项式拟合方法对应的雷达检测概率误差在SCR为10 dB左右时有所增大, 但此误差绝对值仍明显小于传统分析方法对应的检测概率误差绝对值。可见, 采用多项式对杂波幅度拖尾导致的虚警概率进行单独建模, 并据此获得雷达检测门限, 可保证雷达检测性能分析结果具有较高的精度。

4 结论

杂波幅度分布全段拟合建模在杂波拖尾部分往往存在较大误差, 这会使实际雷达系统检测门限计算存在较大误差, 最终导致雷达目标检测性能分析精度不高。对此, 本文提出了采用多项式对杂波拖尾导致的虚警率拖尾进行单独拟合建模的方法。在此基础上, 计算检测门限, 分析雷达检测性能。雷达外场探测无人机试验数据分析结果表明，对杂波拖尾导致的虚警概率采用多项式拟合建模, 由此获得的雷达检测门限较精确, 雷达无人机检测性能分析结果精度明显高于传统方法。

值得一提的是, 实际雷达系统的虚警率通常很低, 雷达检测门限的设置与杂波幅度拖尾分布直接相关, 因此在杂波幅度分布建模时可重点对杂波拖尾部分进行建模。本文采用多项式对虚警概率进行拟合建模的思路同样适用于杂波幅度拖尾建模。

参考文献

QUILTER T, BAKER C. The application of staring radar to the detection and identification of small unmanned aircraft systems in Monaco[C]//Proc. of the 18th International Radar Symposium, 2017.

[本文引用: 1]

KIM K , VNEY M , MULGREW B .

Coherent track-before-detect with micro-Doppler signature estimation in array radars

[J]. IET Radar, Sonar and Navigation, 2020, 14 (4): 572- 585.

DOI:10.1049/iet-rsn.2019.0319     

OH B S , LIN Z .

Extraction of global and local micro-Doppler signature features from FMCW radar returns for UAV detection

[J]. IEEE Trans.on Aerospace and Electronic Systems, 2021, 57 (2): 1351- 1360.

DOI:10.1109/TAES.2020.3034020      [本文引用: 1]

YANG Y , BAI Y , WU J N , et al.

Experimental analysis of fully polarimetric radar returns of a fixed-wing UAV

[J]. IET Radar, Sonar and Navigation, 2020, 14 (4): 525- 531.

DOI:10.1049/iet-rsn.2019.0312      [本文引用: 1]

ZHAO Y C , SU Y .

The extraction of micro-Doppler signal with EMD algorithm for radar-based small UAVs' detection

[J]. IEEE Trans.on Instrumentation and Measurement, 2020, 69 (3): 929- 940.

DOI:10.1109/TIM.2019.2905751     

NIE W , HAN Z C , LI Y , et al.

UAV detection and localization based on multi-dimensional signal features

[J]. IEEE Sensors Journal, 2022, 22 (6): 5150- 5162.

DOI:10.1109/JSEN.2021.3105229     

杨勇, 王雪松, 张斌.

基于时频检测与极化匹配的雷达无人机检测方法

[J]. 电子与信息学报, 2021, 43 (3): 509- 515.

[本文引用: 2]

YANG Y , WANG X S , ZHANG B .

Radar detection of unmanned aerial vehicles based on time-frequency detection and polarization matching

[J]. Journal of Electronics & Information Technology, 2021, 43 (3): 509- 515.

[本文引用: 2]

CUI G L , DE-MAIO A , CAROTENUTO V , et al.

Performance prediction of the incoherent detector for a Weibull fluctuating target

[J]. IEEE Trans.on Aerospace and Electronic Systems, 2014, 50 (3): 2176- 2184.

DOI:10.1109/TAES.2014.130040      [本文引用: 2]

GARCÍA F D A , ROFRIGUEZ A C F , FRAIDENRAICH G .

Highly accurate closed-form approximation for the probability of detection of Weibull fluctuating targets in noncoherent detectors

[J]. IEEE Trans.on Aerospace and Electronic Systems, 2022, 58 (1): 47- 57.

DOI:10.1109/TAES.2021.3096867     

YANG Y , XIAO S P , WANG X S , et al.

Performance analysis of radar detection for correlated gamma fluctuating targets in K distributed sea clutter

[J]. Digital Signal Processing, 2018, 79 (1): 136- 141.

[本文引用: 1]

CARRETERO-MOYA J , DE MAIO A , GISMERO-MENOYO J , et al.

Experimental performance analysis of distributed target coherent radar detectors

[J]. IEEE Trans.on Aerospace and Electronic Systems, 2012, 48 (3): 2216- 2238.

DOI:10.1109/TAES.2012.6237589      [本文引用: 1]

ROSENBERG L , BOCQUET S .

Non-coherent radar detection performance in medium grazing angle X-band sea clutter

[J]. IEEE Trans.on Aerospace and Electronic Systems, 2017, 53 (2): 669- 682.

DOI:10.1109/TAES.2017.2651718     

YOOH B , LEE H .

Practical approach to radar detection performance for NCI system

[J]. IEEE Sensors Letters, 2022, 6 (6): 1500504.

[本文引用: 1]

LUONG D , BALAJI B , RAJAN S .

Performance prediction for coherent noise radars using the correlation coefficient

[J]. IEEE Access, 2022, 10, 8627- 8633.

DOI:10.1109/ACCESS.2021.3135292     

XUE J , XU S W , LIU J , et al.

Model for non-Gaussian sea clutter amplitudes using generalized inverse Gaussian texture

[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16 (6): 892- 896.

DOI:10.1109/LGRS.2018.2886782      [本文引用: 1]

XU S W , WANG Z X , BAI X H , et al.

Optimum and near-optimum coherent CFAR detection of radar targets in compound-Gaussian clutter with generalized inverse Gaussian texture

[J]. IEEE Trans.on Aerospace and Electronic Systems, 2022, 58 (3): 1692- 1706.

DOI:10.1109/TAES.2021.3120045      [本文引用: 1]

HUANG P H , ZOU Z H , XIA X G , et al.

A statistical model based on modified generalized-K distribution for sea clutter

[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19, 8015805.

YANG Y , XIAO S P , WANG X S , et al.

Performance analysis of radar detection for correlated gamma fluctuating targets in K distributed sea clutter

[J]. Digital Signal Processing, 2018, 79, 136- 141.

DOI:10.1016/j.dsp.2018.05.001      [本文引用: 1]

丁昊, 董云龙, 刘宁波, 等.

海杂波特性认知研究进展与展望

[J]. 雷达学报, 2016, 5 (5): 499- 416.

[本文引用: 1]

DING H , DONG Y L , LIU N B , et al.

Overview and prospects of research on sea clutter property cognition

[J]. Journal of Radars, 2016, 5 (5): 499- 516.

[本文引用: 1]

杜延磊, 高帆, 刘涛, 等.

基于数值仿真的X波段极化SAR海杂波统计建模与特性分析

[J]. 系统工程与电子技术, 2021, 43 (10): 2742- 2755.

URL    

DU Y L , GAO F , LIU T , et al.

Statistical modeling and characteristic analysis of polarimetric SAR sea clutter at X-band based on numerical simulations

[J]. Systems Engineering and Electronics, 2021, 43 (10): 2742- 2755.

URL    

ROSENBERG L , WATTS S , GRECO M S .

Modeling the statistics of microwave radar sea clutter

[J]. IEEE Aerospace and Electronic Systems Magazine, 2019, 34 (10): 44- 75.

DOI:10.1109/MAES.2019.2901562     

GRECO M , GINI F , RANGASWAMY M .

Statistical analysis of measured polarimetric clutter data at different range resolutions

[J]. IEE Proceedings of Radar Sonar and Navigation, 2006, 153 (6): 473- 481.

DOI:10.1049/ip-rsn:20060045     

YANG Y , XIAO S P , WANG X S , et al.

Statistical distribution of polarization ratio for radar sea clutter

[J]. Radio Science, 2017, 52 (8): 981- 987.

DOI:10.1002/2017RS006371      [本文引用: 1]

KAY S . Fundamentals of statistical signal processing, volume Ⅱ: detection theory[M]. New Jersey: Prentice Hall, 1998.

[本文引用: 1]

WARD K D , TOUGH R J A , WATTS S . Sea clutter: scattering, the K distribution and radar performance[M]. 2nd ed London: The Institution of Engineering and Technolog, 2013.

[本文引用: 1]

ROSENBERG L , WATTS S . Radar sea clutter: modelling and target detection[M]. London: The Institution of Engineering and Technology, 2021.

[本文引用: 1]

KAY S . Fundamentals of statistical signal processing, volume Ⅰ: estimation theory[M]. New Jersey: Prentice Hall, 1993.

[本文引用: 1]

BRONSHTEIN I N , SEMENDYAYEV K A , MUSIOL G , et al. Handbook of mathematics[M]. 5th ed Berlin: Springer-Verlag, 2007.

[本文引用: 2]

ANASTASSOPOULOS V , LAMPROPOULOS G A , DROSOPOULOS A , et al.

High resolution radar clutter statistics

[J]. IEEE Trans.on Aerospace and Electronic Systems, 1999, 35 (1): 43- 60.

DOI:10.1109/7.745679      [本文引用: 1]

朱玲, 江朝抒, 陈祝明.

KS, χ2检验方法的K分布杂波参数估计研究

[J]. 电子科技大学学报, 2008, 37 (S1): 13- 16.

[本文引用: 2]

ZHU L , JIANG C S , CHE Z M .

Parameter estimation study of K-distribution based on the goodness-of-fit test

[J]. Journal of University of Electronic Science and Technology of China, 2008, 37 (S1): 13- 16.

[本文引用: 2]

/

〈 〉

京ICP备11035014号-5
版权所有 © 2019 北京航天情报与信息研究所《系统工程与电子技术》编辑部
通讯地址：北京市142信箱32分箱《系统工程与电子技术》编辑部(100854)
电　话：(010)68388406/68386014    E-mail：xtgcydzjs@126.com(系统工程与电子技术)/jseeoffice@126.com(JSEE)
本系统由北京玛格泰克科技发展有限公司设计开发