0 引言
基于深度学习的调制识别方法, 除直接将基带信号输入神经网络, 还可提取信号的特征输入神经网络, 如时频图、星座图、高阶累积量等。Kumar等[3]基于高斯信道生成信号星座密度矩阵, 采用图像的方式利用残差神经网络实现了8种调制信号的识别。Xie等[4]在高斯信道下利用高阶累积量特征和深度神经网络(deep neural network, DNN)实现了6种数字调制信号的识别。郝云飞[5]基于稀疏自编码(sparse autoencoder, SAE)网络和生成对抗网络提出重构判别网络, 结合高阶谱在高斯信道下实现了3种无人机调制信号的开集识别。王自维等[6]将无人机遥控信号的时频图输入LeNet-5模型, 在低信噪比下实现了相移键控(phase shift keying, PSK)、频移键控(frequency-shift keying, FSK)、正交振幅调制(quadrature amplitude modulation, QAM)信号的类间识别和类内识别。然而, 上述基于深度学习的调制识别方法存在以下问题: 计算量较大, 如提取信号时频图特征时计算量较大[7-9]; 考虑的信道条件过于理想, 通常在高斯信道下[5, 10-13]; 低信噪比下识别性能较差[3, 14-15]。
无人机集群通信电磁环境复杂, 不可避免地会出现时延、频移、用户干扰等现象。目前国内外针对无人机集群通信波形识别的研究极少, 而现有的调制识别算法因其存在信道条件过于理想、信噪比低、鲁棒性差等问题, 难以满足无人机集群通信波形识别的要求, 因此本文提出了一种复杂多径环境下的无人机集群通信波形识别算法。该算法在低信噪比下抗干扰能力强, 在战场环境下, 尤其是敌方采用小功率发射机或信号传播损耗较大的场景下具备应用价值。本文第1部分为引言; 第2部分为系统模型, 建立了Alpha脉冲干扰下无人机集群通信多径衰落信道; 第3部分基于广义循环平稳特征建立了复杂多径环境下的无人机集群通信波形特征矩阵; 第4部分建立了SAE网络无人机集群通信波形识别模型; 第5部分为仿真结果与分析; 第6部分为结论。
1 系统模型
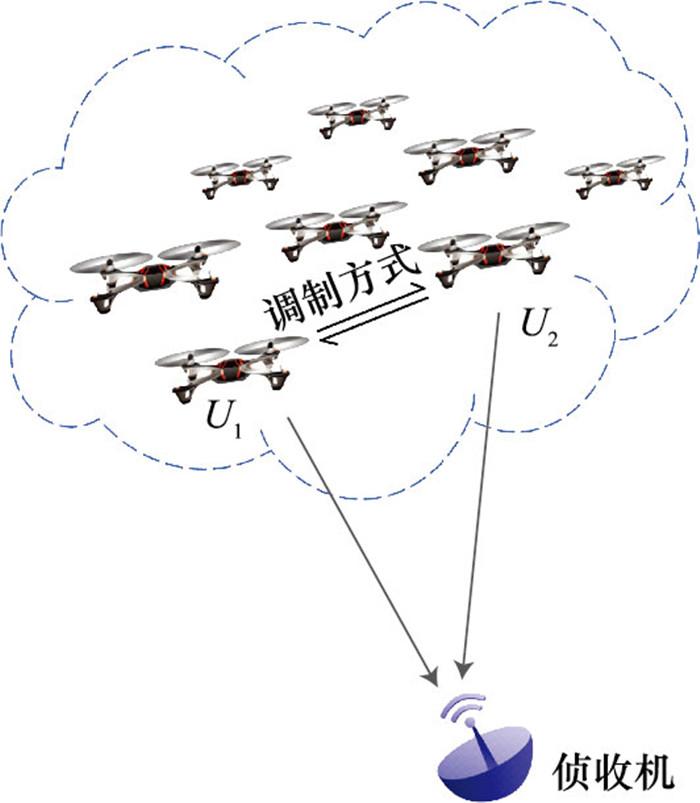
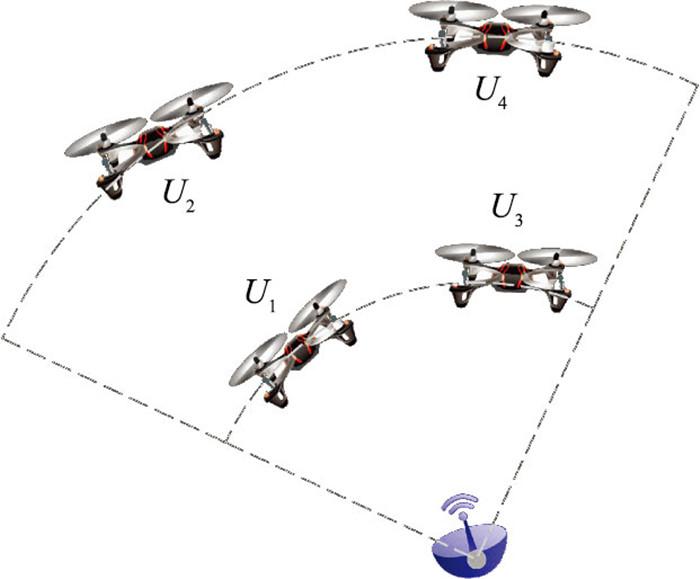
本文考虑的无人机集群通信场景如图 1所示, 集群内的多个用户利用正交的方式进行通信, 如当集群内的用户U1和U2进行通信时, 侦收机可分别获得两个用户发送的信号。集群内所有用户采用同种调制方式, 包括二进制PSK(binary PSK, BPSK)、正交PSK(quadrature PSK, QPSK)、2FSK、4FSK、二进制幅度键控(2 amplitude shift keying, 2ASK)、4ASK、最小频移键控(minimum shift keying, MSK)。
图1
无人机集群通信的电磁环境复杂, 不可避免地会产生多径衰落、时延、频移和用户间干扰等现象。本文采用经典的抽头延迟线(tapped delay line, TDL)信道模型, 其中无人机多径衰落信道基于3GPP TR 901.38无线电信道模型规范[16]设置信道参数, 用户间干扰采用Alpha脉冲噪声。
1.1 多径衰落信道
无人机多径衰落信道的冲激响应可表示为
式中: Pl、τl和Jl(t)分别为第l条多径所对应的抽头功率、时延和平坦衰落信号发生器的输出(通过Jakes模型[17]实现), 且0≤l≤L-1, L为多径信道的可分辨路径数。
3GPP TR 901.38规范根据实测数据提供了5种TDL信道模型参数, 分别适用于非视距(non-line of sight, NLOS)场景和视距(line of sight, LOS)场景。该报告规定可通过调节均方根(root mean square, RMS)时延扩展获得指定场景下的抽头时延:
式中: τl, model为TDL模型中第l个抽头所对应的标准化时延; DSdesired[ns]为特定场景下的RMS时延扩展。对于含LOS径的信道模型, 用户可通过调节K因子获得指定的Kdesired[dB]。在调节K因子后, 该模型每个抽头对应的功率将调节为
式中: Pl, model为TDL模型中第l个抽头所对应的功率; Kdesired为特定场景下的K因子值; Kmodel为该模型现在的K因子值。
1.2 Alpha脉冲干扰
本文采用Alpha稳定分布脉冲噪声描述用户间的干扰[18]:
式中: α为特征指数; γ为分散系数; β为偏斜参数; υ为位置参数; sgn(t)为符号函数。本文采用α=1.5, β=0, γ=1, υ=0的对称Alpha稳定分布噪声, 定义混合信噪比(mixed signal to noise, MSNR)为
式中: σs2为信号的平均功率。
1.3 接收信号处理流程
侦收机截获的无人机通信信号可表示为
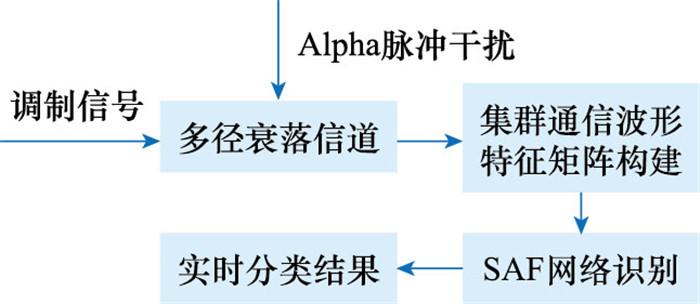
式中: x(t)为发送的调制信号; n(t)为Alpha脉冲干扰。图 2为无人机集群通信波形识别的系统框图, 调制信号在经过Alpha脉冲干扰下的多径衰落信道后被侦收机截获; 随后, 提取信号的广义循环均值和广义循环谱特征, 并构建无人机集群通信波形特征矩阵; 最终, 通过SAE神经网络识别无人机集群通信波形, 输出实时分类结果。
图2
图2
无人机集群通信波形识别系统框图
Fig.2
System block diagram of the unmanned aerial vehicle swarm communication waveform recognition
2 特征矩阵构建
2.1 无人机集群通信波形特征
在无线移动通信中, 数字信号经采样、调制、编码等预处理过程后, 其循环均值和循环谱特征通常会随时间呈周期性变化。定义接收信号r(t)的循环均值为
式中: ε=k/T为循环频率; Mr(t)为信号r(t)的均值。信号r(t)的循环谱密度[19]Srε(f)表示为
式中: Rrε(τ)为信号r(t)的循环自相关函数, 定义为
当ε=0时, 循环谱密度退化为功率谱密度。
由于Alpha稳定分布噪声的二阶及以上各阶统计量趋于无穷, 需对接收信号进行非线性变换, 将噪声无穷的幅值限制在有限的区间内, 以获得有效的信号特征。经非线性变换[20]后的信号为
式中: Δ=1时, Alpha的噪声抑制效果较好。信号经非线性处理后的特征被称为广义循环均值和广义循环谱。表 1为不同调制类型信号循环均值与循环谱特征离散峰值所对应的循环频率。其中, fc为中心频率, Rb为码元速率。
表1 不同调制信号循环平稳特征
Table 1
| 调制类型 | 循环均值 | f=0截面的循环谱 |
| MASK | ε=fc | ε=2fc |
| BPSK | 无离散峰值 | ε=±(2fc±Rb) |
| QPSK | 无离散峰值 | 无离散峰值 |
| MFSK | ε=fc+fm | ε=±2(fc+fm) |
| MSK | 无离散峰值 | ε=±(2fc±Rb/2) |
2.2 集群通信波形特征矩阵
根据表 1, 选择神经网络的输入特征参数: 对于不同调制信号的循环均值特征, 以循环均值的离散峰值个数ρ1、平均循环均值ρ2和最大离散峰值ρ3作为特征参数; 对于不同调制信号的循环谱特征, 以f=0截面且ε>0时的离散峰值ρ4~ρ8作为特征参数, 即ε=2fc, ε=2fc±Rb和ε=2fc±Rb/2处的循环谱密度峰值。
本文中无人机通信频率为5.8 GHz, 此时大气损耗极小, 可认为电磁波在自由空间传播。考虑无人机集群内存在N个正在通信的用户, 其发射功率、接收功率和载波频率均相同, 无人机用户U1~UN分别距侦收机d1~dN km, 则集群内任意用户Un相对于无人机用户U1的接收信号功率差ΔP(dB)定义为
式中: Δhp为由时变信道导致的接收信号功率差; ΔLp为由两用户距侦收机的距离不同而导致的路径损耗差。以无人机用户1的混合信噪比M为标准, 定义M下的无人机集群通信波形特征矩阵为
式中:
3 基于SAE的集群通信波形识别
本文采用具有稀疏特性的DNN模型的自编码器——SAE[21]完成无人机集群信号的调制识别。与循环神经网络和卷积神经网络等较为经典的网络相比, SAE网络的隐藏层含有稀疏系数, 可以减小过拟合风险, 加速网络的训练和部署。
假设自编码器的输入数据集为{m1, m2, …, mk}, 其中k为样本个数。自编码器的损失函数可以表示为
式中: W和b分别表示自编码器的权重矩阵和各层偏置;
式中:
式中: aj表示隐藏层第j个神经元的激活函数, 则稀疏约束后的总损失函数可表示为
式中:
4 仿真结果与分析
本部分以Matlab为仿真平台, 分别对无人机集群多径衰落信道、无人机通信波形循环平稳特征、7种无人机集群通信波形的识别进行仿真。
4.1 仿真1
仿真1为无人机集群多径衰落信道的仿真, 信道模型参数参考3GPP TR 38.901, 以TDL-A和TDL-D两种信道场景为例, 其中TDL-A为NLOS场景, TDL-D为LOS场景。
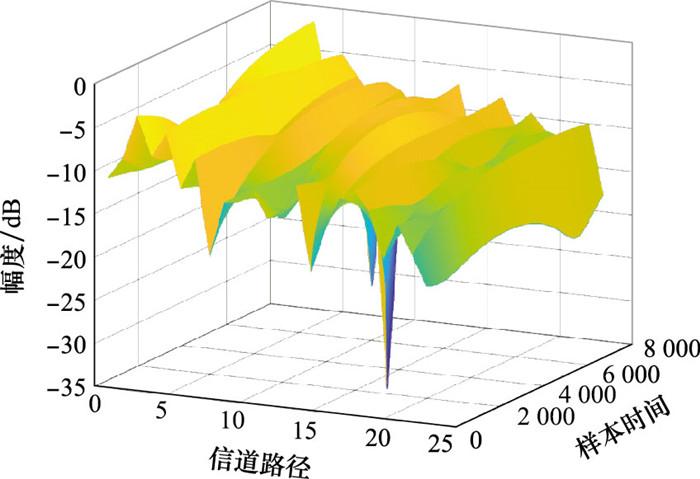
考虑NLOS场景, 无人机通信的载波频率为5.8 GHz, 无人机飞行速率为60 m/s, 此时的最大多普勒频移为1 160 Hz。采用TDL-A模型参数, 根据上述内容, 设置RMS时延扩展为100 ns, 样本点数为8 000 samples, 采样速率fs为16M sample/s。图 3为TDL-A模型路径增益随样本时间和路径个数变换的三维图, 该模型共有23条可分辨路径。
图3
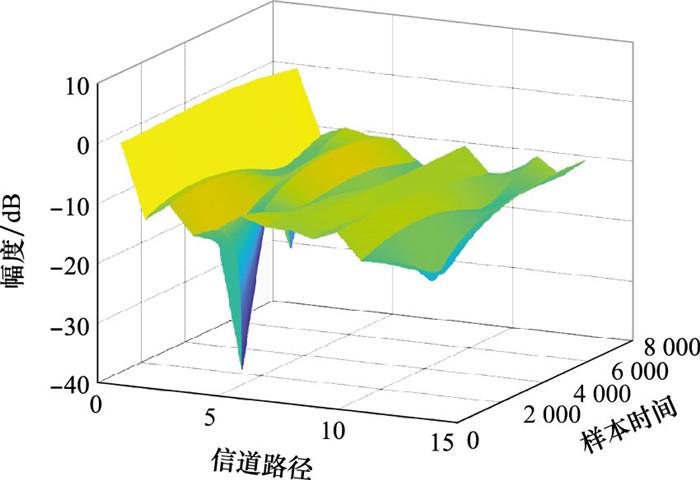
考虑LOS场景, 采用TDL-D模型参数, 设置RMS时延扩展为30 ns, K因子为9 dB, 其余参数不变。图 4为TDL-D模型路径增益随样本时间和路径个数变换的三维图, 该模型共有13条可分辨路径, 其中第一条径为LOS径, 其增益相对其他径更大。
图4
4.2 仿真2
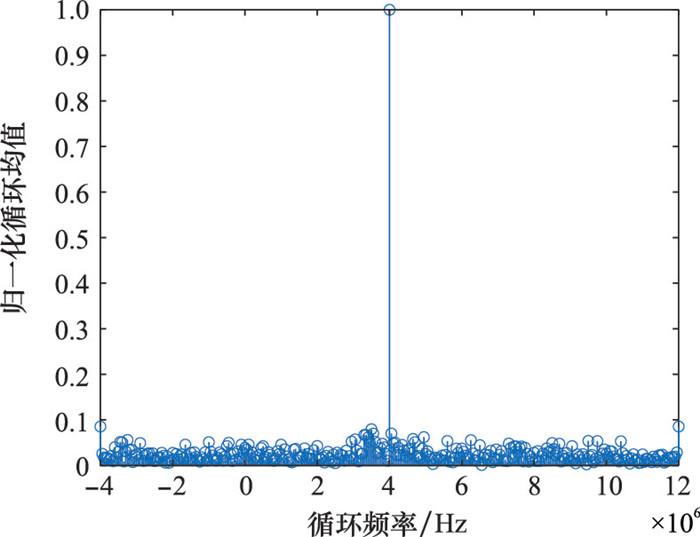
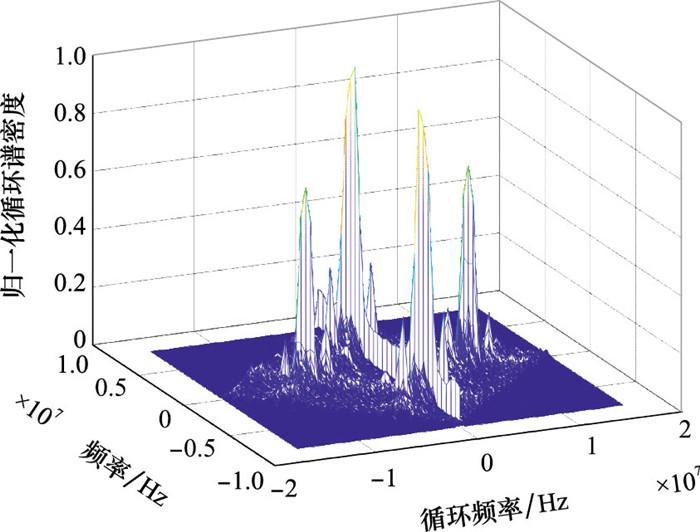
图5
图6
信道模型参数与仿真1中的TDL-D相同, 其他仿真参数如下: 符号个数1 000 symbol, 码元速率Rb为2M symbol/s, 升余弦脉冲成型的滚降系数为0.5, 混合信噪比为0 dB。由于接收信号载波频率为5.8 GHz, 为降低射频采样成本, 将信号下变频至140 MHz, 再进行带通采样。以BPSK信号为例, 接收信号rBPSK(x)带宽为3 MHz。经带通采样后, 其信号功率谱以采样速率fs为周期进行延拓, 低通滤波后, 信号中心频率搬移至4 MHz。
4.3 仿真3
仿真3为基于SAE网络的无人机集群通信波形的识别。考虑集群内存在两无人机用户正在通信, 通信频率为5.8 GHz, 其参数设置如表 2所示。集群内用户可能采用的调制方式类型包括BPSK、QPSK、2FSK、4FSK、2ASK、4ASK、MSK。
表2 信道及无人机参数配置1
Table 2
| 参数 | 无人机1 | 无人机2 |
| 飞行速度/(m/s) | 50.0 | 50.5 |
| 最大多普勒频移/Hz | 967 | 976 |
| TDL-A时延扩展/ns | 100 | 101 |
| TDL-D时延扩展/ns | 30 | 31 |
表3 SAE网络结构参数配置
Table 3
| SAE网络模型 | 参数值 |
| 输入层 | 14 |
| 隐藏层 | (10, 8) |
| 输出层 | 6 |
| 激活函数 | Linear, ReLU, Softmax |
| 优化算法 | L-BFGS |
| 稀疏系数 | 0.1 |
| 稀疏权重因子 | 3 |
| 权重衰减系数 | 0.000 1 |
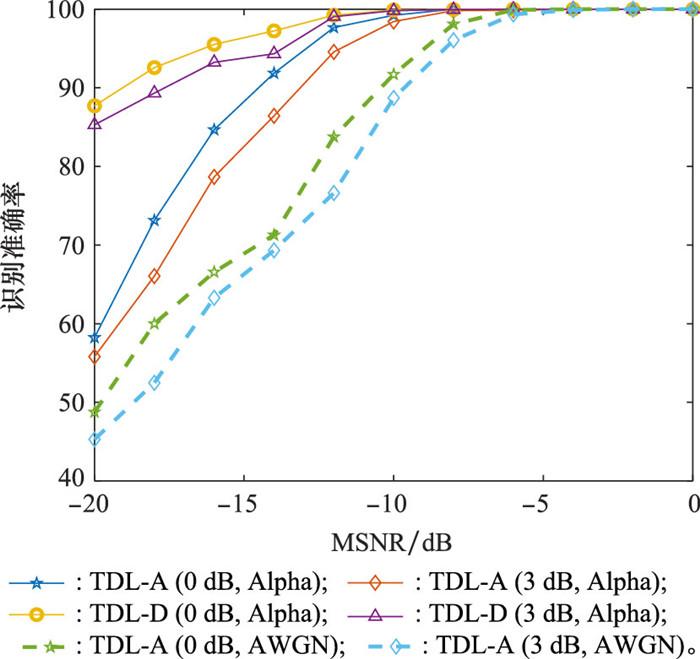
其中, SAE网络中训练集与测试集大小比例为7 ∶3。考虑其路径损耗差ΔLp分别为0 dB和3 dB的场景, 对应地, 两无人机用户相对于侦收机的距离比分别为0.71和1。图 7为不同信道条件下的集群通信波形识别性能曲线, 其中TDL-A(0 dB, Alpha)表示路径损耗差为0 dB时, 信号经TDL-A信道且受Alpha脉冲干扰的情况。
图7
图7
无人机集群通信波形识别性能曲线
Fig.7
Unmanned aerial vehicle swarm communication waveform recognition performance curve
整体上看, 无人机集群通信波形的识别准确率随MSNR增大而递增, 且本文提取的特征在低信噪比下鲁棒性强。从信道上分析, TDL-A信道下的识别准确率优于TDL-D信道。考虑Alpha干扰下路径损耗差为3 dB的情况, 当MSNR为-16 dB时, TDL-D信道下的识别准确率为95.52%, 优于TDL-A信道下约2.5 dB, 这是由于TDL-D信道存在LOS径。从噪声干扰上分析, 集群通信波形的识别准确率在Alpha干扰下比在AWGN噪声下的性能好。考虑TDL-A信道下路径损耗差为3 dB的情况, 当MSNR为-14 dB时, 受Alpha脉冲干扰的识别准确率为86.43%, 优于AWGN噪声下约3.5 dB, 说明本文提取的特征虽适用于AWGN噪声, 但在Alpha干扰下稳健性更好。从路径损耗差分析, 路径损耗差越大, 其无人机集群通信波形的识别准确率越低。考虑Alpha干扰下信号经TDL-A信道的情况, 当MSNR为-14 dB时, 路径损耗差为0 dB的识别准确率为85.17%, 当路径损耗差为3 dB时, 识别准确率为79.61%。
4.4 仿真4
仿真4分析了影响无人机集群通信波形识别性能的因素, 分别从识别方法、集群内通信用户数目、多普勒频移大小3方面进行了分析。
4.4.1 不同识别方法对识别性能的影响
本文选用分类算法中较为经典的K最近邻(K nearest neighbor, KNN)算法和决策树算法作比较。以TDL-A信道模型为例, 考虑集群内存在两架正在通信的无人机用户, 且两用户之间的路径损耗差为0 dB, 其他参数参考表 2。其中, 基于KNN的识别方法采用欧式距离作为距离度量, K值设置为10;基于决策树的识别方法采用基尼多样性指数作为分裂准则, 最大分裂数设置为8;基于SAE网络的识别方法参数与仿真3相同。
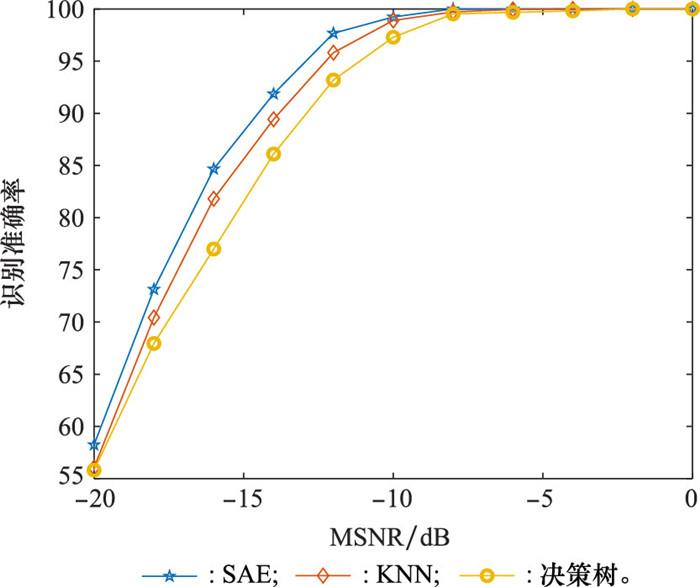
图 8为TDL-A信道下采用不同识别方法后的集群通信波形识别性能曲线。当MSNR为-8 dB时, 3种识别方法的识别准确率几乎达100%, 说明本文提取的广义循环平稳特征稳健性好、易于识别。同时, 基于SAE网络的识别方法识别性能整体优于KNN算法和决策树算法, 当MSNR为-14 dB时, 基于SAE的识别方法识别准确率为91.81%, 优于KNN算法约1 dB, 优于决策树算法约2 dB。
图8
图8
不同方法下集群通信波形识别性能曲线
Fig.8
Swarm communication waveform recognition performance curve under different methods
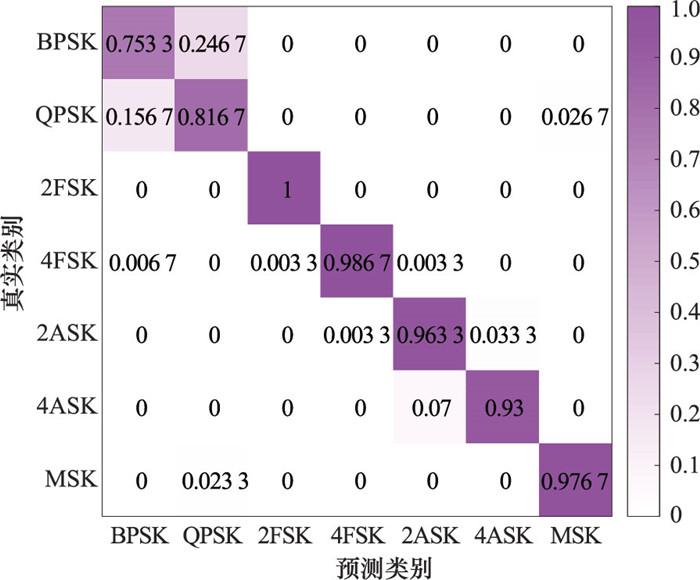
图9
图9
MSNR为-14 dB时的混淆矩阵(SAE算法)
Fig.9
Confusion matrices when MSNR of -14 dB (SAE algorithm)
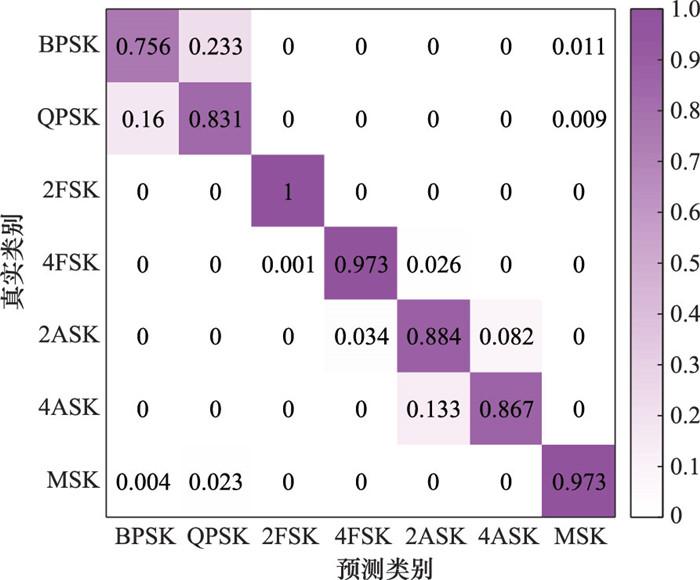
图10
图10
MSNR为-14 dB时的混淆矩阵(KNN算法)
Fig.10
Confusion matrices when MSNR of -14 dB (KNN algorithm)
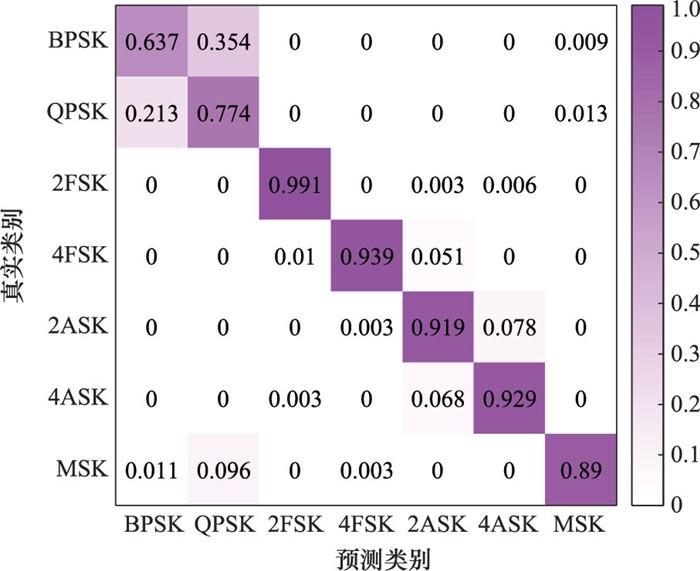
图11
图11
MSNR为-14 dB时的混淆矩阵(决策树算法)
Fig.11
Confusion matrices when MSNR of -14 dB (decision tree algorithm)
4.4.2 集群内通信用户数目对识别性能的影响
图12
图12
通信用户与侦收机位置分布
Fig.12
Location distribution of communication users and reconnaissance machine
表4 信道及无人机参数配置2
Table 4
| 无人机 | 飞行速度/(m/s) | 最大多普勒频移/Hz | 时延扩展/ns |
| 1 | 50.0 | 967 | 100 |
| 2 | 50.5 | 976 | 101 |
| 3 | 51.0 | 986 | 102 |
| 4 | 51.5 | 995 | 103 |
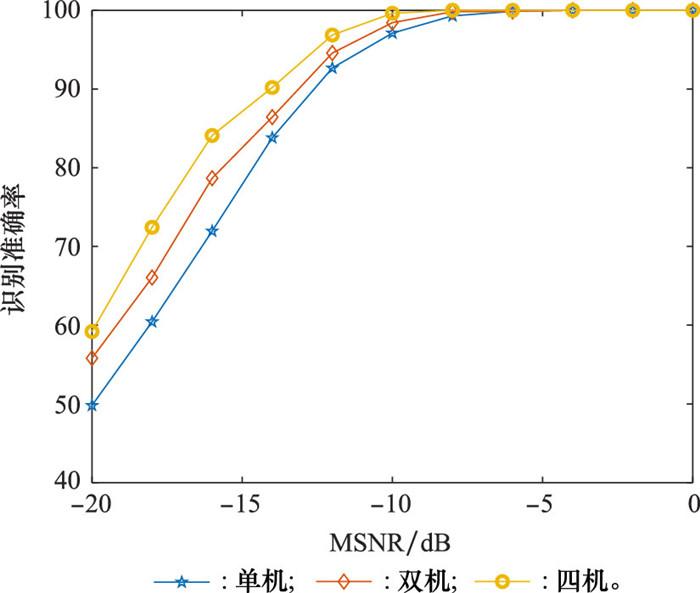
图 13为TDL-A信道下不同通信用户数目的集群波形识别性能曲线, 其中单机场景表示集群中仅存在一个通信用户U1, 双机场景表示集群内的通信用户为U1和U3, 四机场景表示集群内的通信用户为U1~U4。
图13
图13
不同通信用户数下集群通信波形识别性能曲线
Fig.13
Swarm communication waveform recognition performance curve with different number of users
由图 13可知, 随着集群内通信用户数目的增多, 集群通信波形的识别准确率有所提升。当MSNR为-18 dB时, 集群内通信用户数目为1、2、4时, 所对应的识别准确率分别为60.43%、66.5%、72.43%, 这是由于集群内通信用户数越多, 侦收机截获的信号样本越丰富, 提取的特征数量越多。
4.4.3 多普勒频移大小对识别性能的影响
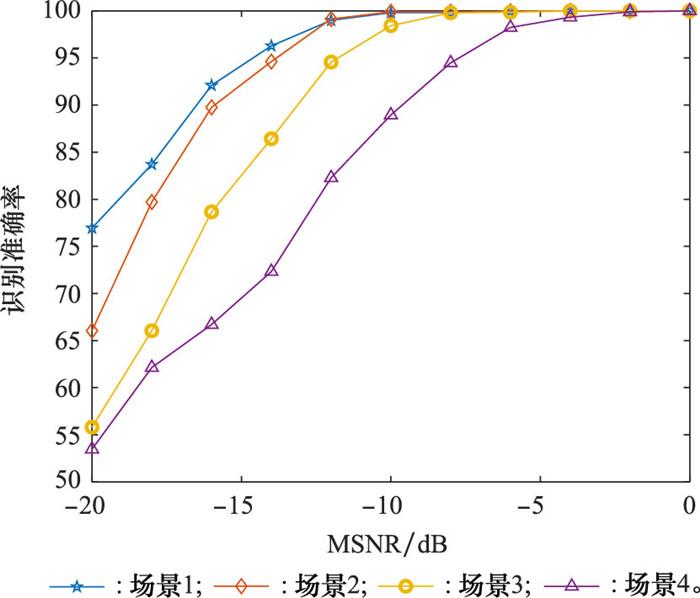
无人机的飞行速度会影响最大多普勒频移的数值, 从而影响无人机集群波形的识别准确率。考虑两无人机用户的路径损耗差ΔLp为3 dB的场景, 采用TDL-A模型, 无人机通信频率为5.8 GHz, 其他参数参考表 5。
表5 信道及无人机参数配置3
Table 5
| 场景 | 参数 | 无人机1 | 无人机2 |
| 所有场景 | 时延扩展/ns | 100 | 101 |
| 场景1 | 飞行速度/(m/s) | 15 | 15.5 |
| 最大多普勒频移/Hz | 290 | 300 | |
| 场景2 | 飞行速度/(m/s) | 25 | 25.5 |
| 最大多普勒频移/Hz | 483 | 493 | |
| 场景3 | 飞行速度/(m/s) | 50 | 50.5 |
| 最大多普勒频移/Hz | 967 | 976 | |
| 场景4 | 飞行速度/(m/s) | 70 | 70.5 |
| 最大多普勒频移/Hz | 1 353 | 1 363 |
图14
图14
不同场景下集群通信波形识别性能曲线
Fig.14
Swarm communication waveform recognition performance curve under different scenes
5 结论
本文提出了一种复杂多径环境下的无人机集群通信波形识别算法, 该算法充分考虑了无人机通信过程中存在的多径衰落、时延、频偏、干扰等问题, 实现了7种无人机集群通信波形的识别, 包括BPSK、QPSK、2FSK、4FSK、2ASK、4ASK、MSK。仿真结果表明: 所构造的无人机集群通信波形特征向量在多普勒频移、多径时延和Alpha脉冲干扰存在的环境下具备良好的鲁棒性, 所建立的SAE无人机集群通信波形识别模型性能优于传统的KNN算法和决策树算法。同时, 本文提出的无人机集群通信波形识别算法在低信噪比下的识别准确率较高, 在信噪比为-10 dB时仍能保证80%以上的识别准确率。
参考文献
一种新的贝叶斯调制分类算法
[J].
A novel Bayesian modulation classification algorithm
[J].
基于时频能量谱纹理特征的跳频调制方式识别
[J].
Identification of frequency hopping modulation mode based on time-frequency energy spectrum texture features
[J].
Automatic modulation classification based on constellation density using deep learning
[J].DOI:10.1109/LCOMM.2020.2980840 [本文引用: 2]
Deep learning in digital modulation recognition using high order cumulants
[J].
基于改进LeNet-5模型的无人机遥控信号调制方式识别算法
[J].
Recognition algorithm of UAV remote control signal modulation mode based on improved LeNet-5 model
[J].
Deep neural network compression technique towards efficient digital signal modulation recognition in edge device
[J].DOI:10.1109/ACCESS.2019.2913945 [本文引用: 1]
Modulation format recognition and OSNR estimation using CNN-based deep learning
[J].
Automatic modulation classification using convolutional neural network with features fusion of SPWVD and BJD
[J].DOI:10.1109/TSIPN.2019.2900201 [本文引用: 1]
基于ICA和特征提取的MIMO信号调制识别算法
[J].
A modulation identification algorithm of MIMO signal based on ICA and feature extraction
[J].
Modulation classification based on signal constellation diagrams and deep learning
[J].
基于轻量级深度神经网络的电磁信号调制识别技术
[J].
Electromagnetic signal modulation identification technology based on lightweight deep neural network
[J].
基于信息熵和GA-ELM的调制识别算法
[J].
Modulation identification algorithm based on information entropy and GA-ELM
[J].
基于集成学习与特征降维的小样本调制识别方法
[J].
Few-sample modulation recognition method based on ensemble learning and feature dimensionality reduction
[J].
软件通信适配器的调制模式识别算法
[J].
Modulation pattern recognition algorithm for software communication adapter
[J].
Automatic modulation classification using deep learning based on sparse autoencoders with nonnegativity constraints
[J].