Systems Engineering and Electronics ›› 2025, Vol. 47 ›› Issue (11): 3672-3684.doi: 10.12305/j.issn.1001-506X.2025.11.16
• Systems Engineering • Previous Articles
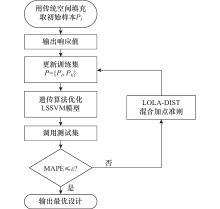
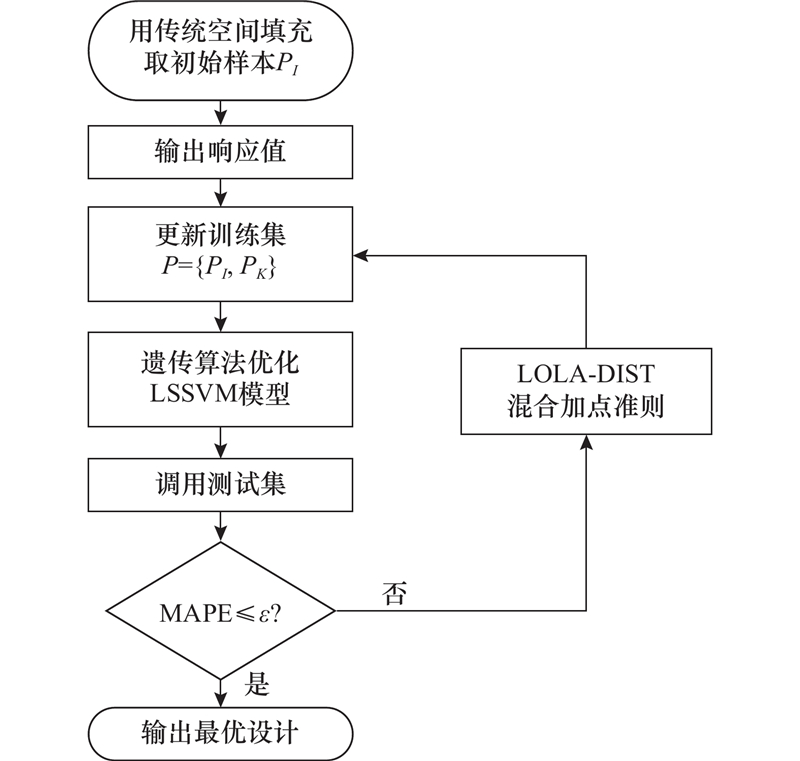
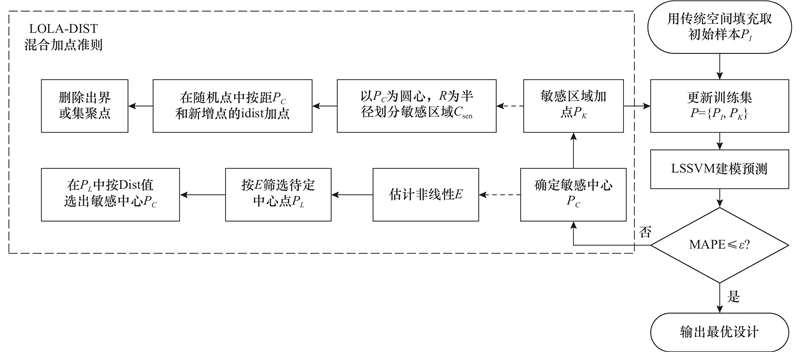
LOLA-DIST sequential design method based on hybrid sampling criterion
Jian ZHONG, Zhijun CHENG, Zhengqiang PAN, Jun FAN, Tianyu LIU
- School of Systems Engineering,National University of Defense Technology,Changsha 410073,China
-
Received:2022-09-20Online:2025-11-25Published:2025-12-08 -
Contact:Zhijun CHENG
CLC Number:
Cite this article
Jian ZHONG, Zhijun CHENG, Zhengqiang PAN, Jun FAN, Tianyu LIU. LOLA-DIST sequential design method based on hybrid sampling criterion[J]. Systems Engineering and Electronics, 2025, 47(11): 3672-3684.
share this article
Table 2
Comparison of optimization results of different experimental designs with same samples"
| 函数序号 | 函数名 | 维度 | 样本数 | LOLA-DIST | LOLA-Vorinoi | 随机设计 | LHS |
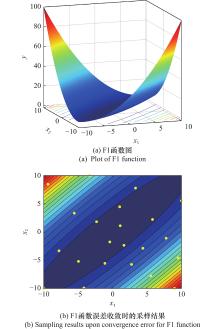
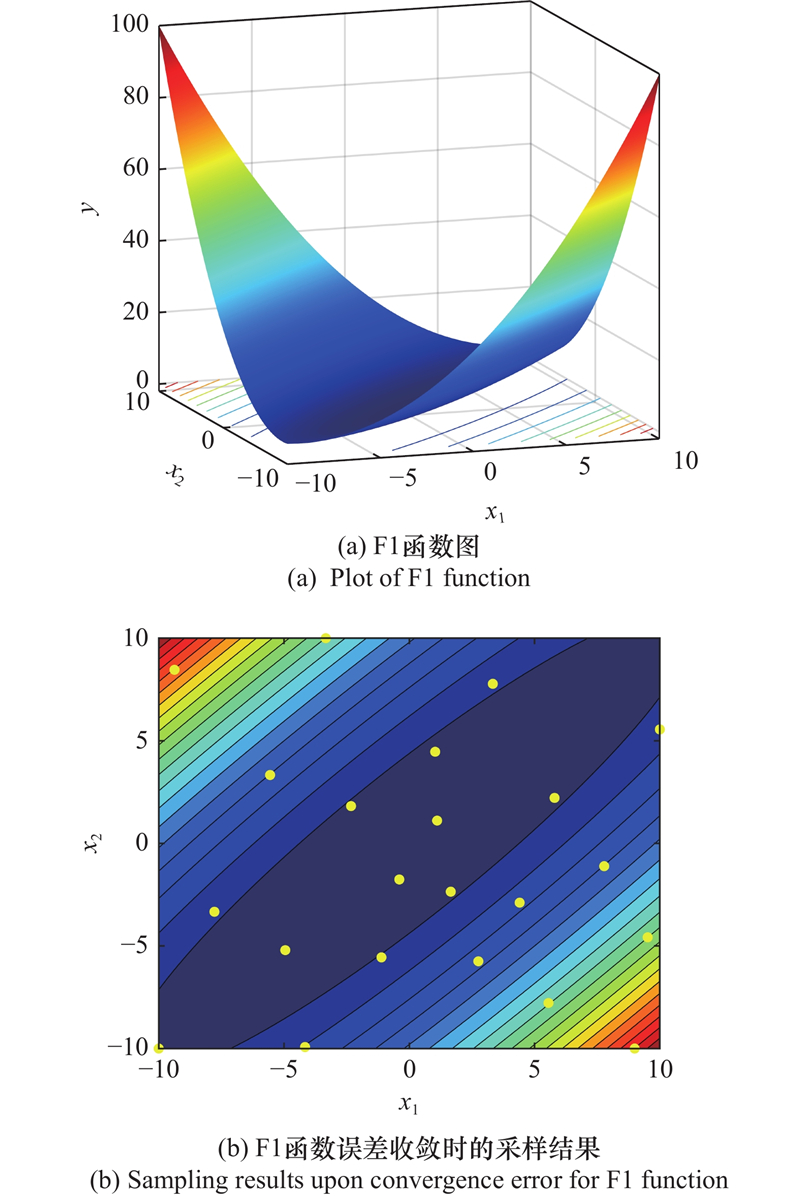
| F1 | MATYAS | 2 | 22 | ||||
| F2 | PEAKS | 2 | 214 | ||||
| F3 | SIX-HUMP CAMEL | 2 | 86 | ||||
| F4 | ACKLEYS | 2 | 40 | ||||
| 10 | 406 | ||||||
| F5 | ROSENBROCK | 4 | 102 | ||||
| F6 | BRATLEY ET AL. | 4 | 46 | ||||
| 5 | 65 | ||||||
| 6 | 178 | ||||||
| F7 | DETTE&PEPELYSHEV | 8 | 190 |
Table 3
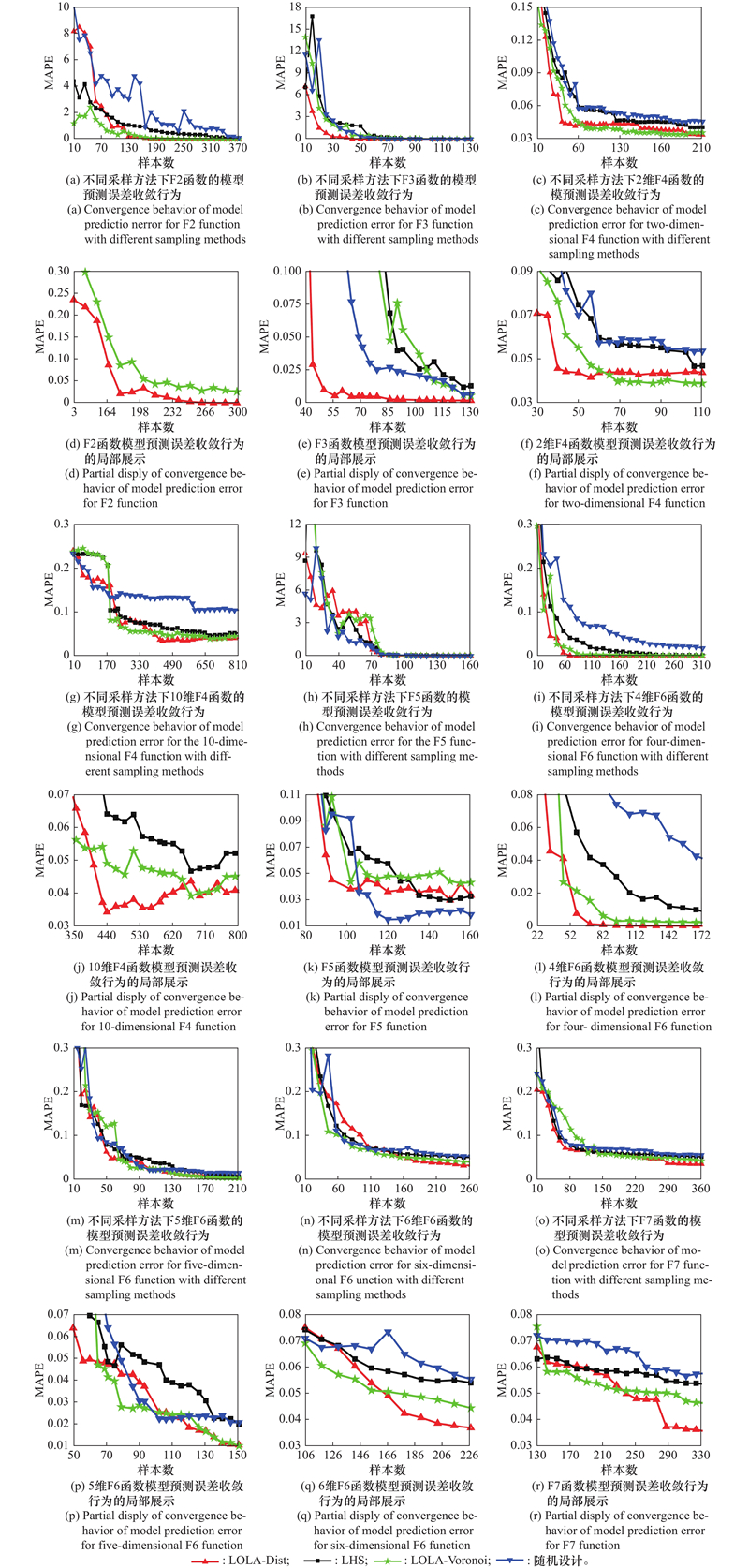
Comparison of model error convergence in different experimental designs (convergence criterion MAPE=0.1)"
| 函数序号 | 维度 | 加点准则 | 收敛点 | MAPE | 函数序号 | 维度 | 加点准则 | 收敛点 | MAPE | |
| F1 | 2 | LOLA-DIST | 12 | F5 | 4 | LOLA-DIST | 88 | |||
| LOLA-Voronoi | 15 | LOLA-Voronoi | 89 | |||||||
| 随机设计 | 28 | 随机设计 | 89 | |||||||
| LHS | 16 | LHS | 91 | |||||||
| F2 | 2 | LOLA-DIST | 166 | F6 | 4 | LOLA-DIST | 24 | |||
| LOLA-Voronoi | 178 | LOLA-Voronoi | 21 | |||||||
| 随机设计 | 238 | 随机设计 | 82 | |||||||
| LHS | 358 | LHS | 46 | |||||||
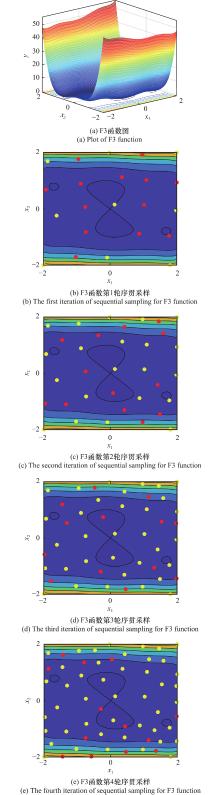
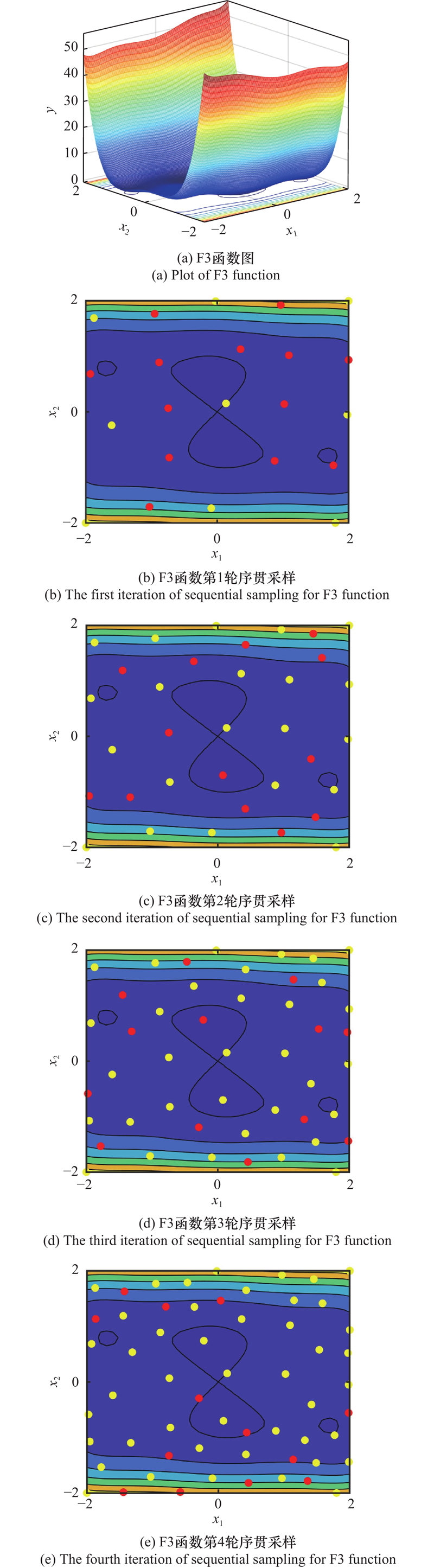
| F3 | 2 | LOLA-DIST | 43 | 5 | LOLA-DIST | 45 | ||||
| LOLA-Voronoi | 85 | LOLA-Voronoi | 61 | |||||||
| 随机设计 | 64 | 随机设计 | 36 | |||||||
| LHS | 82 | LHS | 46 | |||||||
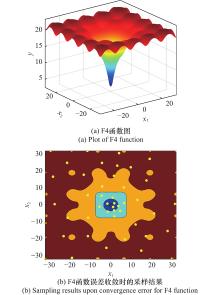
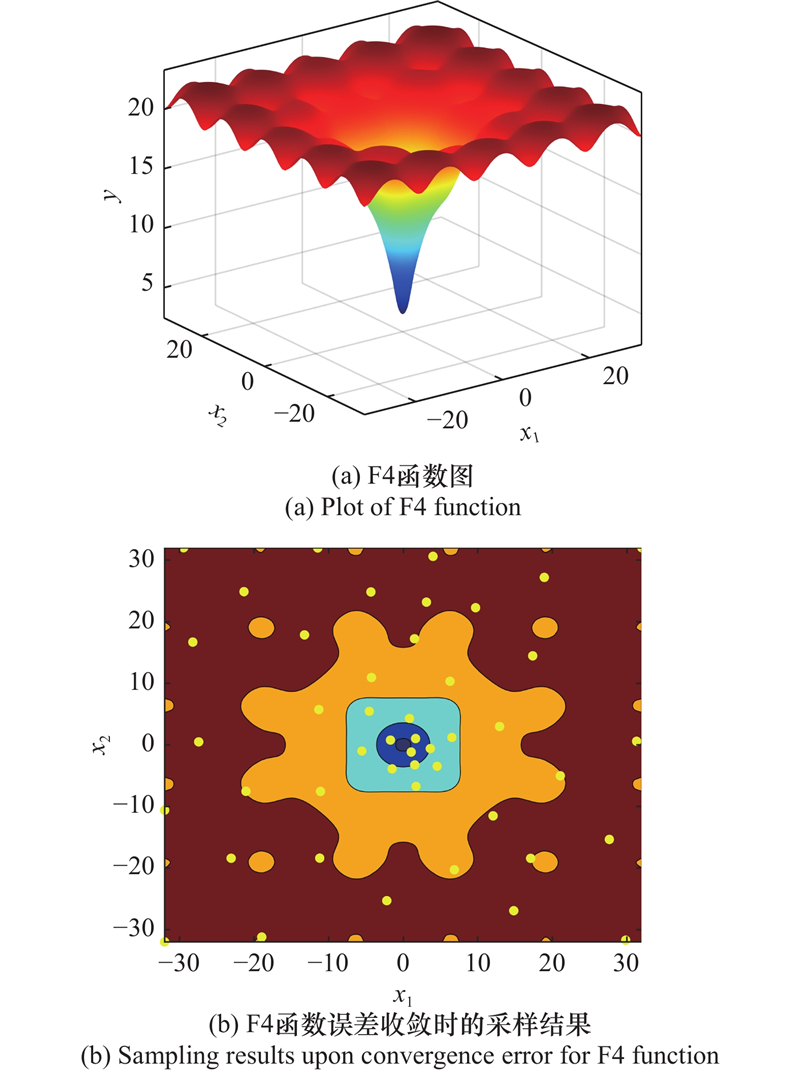
| F4 | 2 | LOLA-DIST | 25 | 6 | LOLA-DIST | 106 | ||||
| LOLA-Voronoi | 30 | LOLA-Voronoi | 70 | |||||||
| 随机设计 | 40 | 随机设计 | 70 | |||||||
| LHS | 35 | LHS | 82 | |||||||
| 10 | LOLA-DIST | 226 | F7 | 8 | LOLA-DIST | 58 | ||||
| LOLA-Voronoi | 190 | LOLA-Voronoi | 94 | |||||||
| 随机设计 | 598 | 随机设计 | 70 | |||||||
| LHS | 238 | LHS | 58 |
Table 4
Comparison of model error convergence in different experimental designs (convergence criterion MAPE=0.05)"
| 函数序号 | 维度 | 加点准则 | 收敛点 | MAPE | 函数序号 | 维度 | 加点准则 | 收敛点 | MAPE | |
| F1 | 2 | LOLA-DIST | 12 | F5 | 4 | LOLA-DIST | 93 | |||
| LOLA-Voronoi | 15 | LOLA-Voronoi | 102 | |||||||
| 随机设计 | 39 | 随机设计 | 106 | |||||||
| LHS | 19 | LHS | 126 | |||||||
| F2 | 2 | LOLA-DIST | 178 | F6 | 4 | LOLA-DIST | 34 | |||
| LOLA-Voronoi | 214 | LOLA-Voronoi | 46 | |||||||
| 随机设计 | 394 | 随机设计 | 166 | |||||||
| LHS | 370 | LHS | 70 | |||||||
| F3 | 2 | LOLA-DIST | 44 | 5 | LOLA-DIST | 56 | ||||
| LOLA-Voronoi | 86 | LOLA-Voronoi | 65 | |||||||
| 随机设计 | 69 | 随机设计 | 79 | |||||||
| LHS | 90 | LHS | 71 | |||||||
| F4 | 2 | LOLA-DIST | 40 | 6 | LOLA-DIST | 166 | ||||
| LOLA-Voronoi | 56 | LOLA-Voronoi | 178 | |||||||
| 随机设计 | 106 | 随机设计 | 286 | |||||||
| LHS | 120 | LHS | 298 | |||||||
| 10 | LOLA-DIST | 406 | F7 | 8 | LOLA-DIST | 238 | ||||
| LOLA-Voronoi | 442 | LOLA-Voronoi | 298 | |||||||
| 随机设计 | > | — | 随机设计 | 490 | ||||||
| LHS | 670 | LHS | 502 |
Table 5
Comparison of model error convergence in different experimental designs (convergence criterion MAPE=0.01)"
| 函数序号 | 维度 | 加点准则 | 收敛点 | MAPE | 函数序号 | 维度 | 加点准则 | 收敛点 | MAPE | |
| F1 | 2 | LOLA-DIST | 13 | F5 | 4 | LOLA-DIST | 173 | |||
| LOLA-Voronoi | 22 | LOLA-Voronoi | 197 | |||||||
| 随机设计 | 54 | 随机设计 | 193 | |||||||
| LHS | 39 | LHS | 210 | |||||||
| F2 | 2 | LOLA-DIST | 238 | F6 | 4 | LOLA-DIST | 58 | |||
| LOLA-Voronoi | 346 | LOLA-Voronoi | 82 | |||||||
| 随机设计 | 466 | 随机设计 | 466 | |||||||
| LHS | 538 | LHS | 178 | |||||||
| F3 | 2 | LOLA-DIST | 50 | 5 | LOLA-DIST | 156 | ||||
| LOLA-Voronoi | 125 | LOLA-Voronoi | 167 | |||||||
| 随机设计 | 125 | 随机设计 | 207 | |||||||
| LHS | 131 | LHS | 201 | |||||||
| F4 | 2 | LOLA-DIST | 322 | 6 | LOLA-DIST | 586 | ||||
| LOLA-Voronoi | 430 | LOLA-Voronoi | 610 | |||||||
| 随机设计 | 490 | 随机设计 | 694 | |||||||
| LHS | 466 | LHS | 658 | |||||||
| F4 | 10 | LOLA-DIST | > | — | F7 | 8 | LOLA-DIST | 682 | ||
| LOLA-Voronoi | > | — | LOLA-Voronoi | 718 | ||||||
| 随机设计 | > | — | 随机设计 | 742 | ||||||
| LHS | > | — | LHS | 802 |
| 1 |
LUALDI P, STURM R, SIEFKES T. Exploration-oriented sampling strategies for global surrogate modeling: a comparison between one-stage and adaptive methods[J]. Journal of Computational Science, 2022, 60, 101603.
doi: 10.1016/j.jocs.2022.101603 |
| 2 | ZHAI G, MA Y F, SONG X, et al. A novel flexible experiment design method[C]//Proc. of the Asian Simulation Conference, 2015: 28−39. |
| 3 | LIN Y, MISTREE F, ALLEN J, et al. Sequential metamodeling in engineering design[C]//Proc. of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 2004: 4304. |
| 4 | LIN Y. An efficient robust concept exploration method and sequential exploratory experimental design[M]. Atlanta: Georgia Institute of Technology, 2004. |
| 5 | DESCHRIJVER D, CROMBECQ K, NGUYEN H M, et al. Adaptive sampling algorithm for macromodeling of parameterized S-Parameter responses[J]. IEEE Trans. on Microwave Theory and Techniques, 2010, 59 (1): 39- 45. |
| 6 |
QAZI M D, LINSHU H, MATEEN P. Hammersley sampling and support-vector-regression-driven launch vehicle design[J]. Journal of Spacecraft and Rockets, 2007, 44 (5): 1094- 1106.
doi: 10.2514/1.22200 |
| 7 | 刘新亮, 郭波. 基于改进ESE算法的多目标优化试验设计方法[J]. 系统工程与电子技术, 2010, 32 (2): 410- 414. |
| LIU X L, GUO B. Multi-objective experimentation design optimization based on modified ESE algorithms[J]. Systems Engineering and Electronics, 2010, 32 (2): 410- 414. | |
| 8 |
PALAR P S, SHIMOYAMA K. On efficient global optimization via universal Kriging surrogate models[J]. Structural and Multidisciplinary Optimization, 2018, 57 (6): 2377- 2397.
doi: 10.1007/s00158-017-1867-1 |
| 9 | 雷永林, 王言, 于芹章, 等. 面向复杂仿真元建模的序贯近邻探索试验设计方法[J]. 系统工程与电子技术, 2021, 43 (5): 1232- 1239. |
| LEI Y L, WANG Y, YU Q Z, et al. Design method of sequential neighbor exploratory experimental for complex simulation metamodeling[J]. Systems Engineering and Electronics, 2021, 43 (5): 1232- 1239. | |
| 10 | PANTULA P D, MIRIYALA S S, MITRA K. Simultaneous knowledge discovery and development of smart neuro-fuzzy surrogates for online optimization of computationally expensive models[C]//Proc. of the Indian Control Conference, 2017: 260−267. |
| 11 | BURKARDT J, GUNZBURGER M, PETERSON J, et al. User manual and supporting information for library of codes for centroidal voronoi point placement and associated zeroth, first, and second moment determination[J]. Office of Scientific & Technical Information Technical Reports, 2002, 15 (26): 399- 406. |
| 12 | GUNZBURGER M. Advances in studies and applications of centroidal voronoi tessellations[J]. Numerical Mathematics Theory Methods & Applications, 2010, 3 (2): 119- 142. |
| 13 | CROMBECQ K. Surrogate modeling of computer experiments with sequential experimental design[D]. Belgium: Ghent University, 2011. |
| 14 |
KE F, YUCHEN Z, PING M A. An adaptive sequential experiment design method for model validation[J]. Chinese Journal of Aeronautics, 2020, 33 (6): 1661- 1672.
doi: 10.1016/j.cja.2019.12.026 |
| 15 | COHN H, KUMAR A. Universally optimal distribution of samples on spheres[J]. Journal of the American Mathematical Society, 2007, 20(1): 99−148. |
| 16 |
JONES D R, SCHONLAU M, WELCH W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13 (4): 455- 492.
doi: 10.1023/A:1008306431147 |
| 17 | 张建侠, 马义中, 欧阳林寒, 等. 基于Kriging模型的多点加点准则和并行代理优化算法[J]. 系统工程理论与实践, 2020, 40 (1): 251- 261. |
| ZHANG J X, MA Y Z, OUYANG L H, et al. A multi-samples infill sampling criterion and parallel surrogate-based optimization algorithm based on Kriging model[J]. System Engineering Theory and Practice, 2020, 40 (1): 251- 261. | |
| 18 |
LAURENCEAU J, MEAUX M, MONTAGNAC M, et al. Comparison of gradient-based and gradient-enhanced response-surface-based optimizers[J]. AIAA Journal, 2010, 48 (5): 981- 994.
doi: 10.2514/1.45331 |
| 19 |
MUTONKOLE N, VILLIERS D D. Multivariate adaptive sampling of parameterized antenna responses[J]. IEEE Trans. on Antennas and Propagation, 2017, 65 (3): 1073- 1080.
doi: 10.1109/TAP.2017.2653761 |
| 20 | HERVIS S Y, PLETS D, MARTINEZ A R, et al. Tool for recovering after meteorological events using a real-time REM and IoT management platform[J]. Wireless Communications and Mobile Computing, 2019, 2019, 1- 13. |
| 21 | ZHOU X J, JIANG T, ZHOU Z H, et al. Sequential-support vector regression based online robust parameter design[J]. Computers & Industrial Engineering, 2021, 158, 107391. |
| 22 | VIANA F, HAFTKA R. Surrogate-based optimization with parallel simulations using the probability of improvement[C]//Proc. of the13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, 2010: 9392. |
| 23 | 李正良, 彭思思, 王涛. 基于混合加点准则的近似模型优化设计方法[J]. 工程力学, 2022, 39 (1): 27- 33. |
| LI Z L, PENG S S, WANG T. A surrogate-based optimization design method based on hybrid infill sampling criterion[J]. Engineering Mechanics, 2022, 39 (1): 27- 33. | |
| 24 |
LIU H T, SHEN L X, MENG J G, et al. A multi-response adaptive sampling approach for global metamodeling[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018, 232 (1): 3- 16.
doi: 10.1177/0954406216672250 |
| 25 |
BHATTACHARYYA, BISWARUP. A critical appraisal of design of experiments for uncertainty quantification[J]. Archives of Computational Methods in Engineering: State of the Art Reviews, 2018, 25 (3): 727- 751.
doi: 10.1007/s11831-017-9211-x |
| 26 | 缪继华. 基于支持向量回归模型的序列采样方法研究[D]. 武汉: 华中科技大学, 2017. |
| MIAO J H. A sequential sampling method based on support vector regression[D]. Wuhan:Hua zhong University of Science and Technology, 2017. | |
| 27 | 季泽. 基于最小二乘支持向量回归的序贯设计与建模方法研究[D]. 郑州: 郑州大学, 2019. |
| JI Z. Sequential design and modeling methods based on the LS-SVR[D]. Zhengzhou: Zhengzhou University, 2019. | |
| 28 | WANG W Y, DOU F, XUAN Y, et al. Load forecasting method based on SVR under electricity market reform[C]//Proc. of the Conference Series: Earth and Environmental Science, 2020, 467(1): 012201. |
| 29 | 尤杨, 金光, 潘正强, 等. 约束空间近似正交的空间填充试验设计方法[J]. 系统工程与电子技术, 2021, 43 (7): 1831- 1837. |
| YOU Y, JING G, PAN Z Q, et al. Nearly-orthogonal space-filling experimental design method for constrained spaces[J]. Systems Engineering and Electronics, 2021, 43 (7): 1831- 1837. | |
| 30 | 姜维, 余义志, 蔡伯根, 等. LSSVM增强的受限环境列车定位精度优化方法[J]. 铁道学报, 2022, 44 (1): 65- 70. |
| JIANG W, YU Y Z, CAI B G, et al. Optimization method for integrated positioning accuracy of trains in restricted environment based on LSSVM[J]. Journal of the China Railway Society, 2022, 44 (1): 65- 70. | |
| 31 |
CHICK S E, BRANKE J, SCHMIDT C. Sequential sampling to myopically maximize the expected value of information[J]. Informs Journal on Computing, 2010, 22 (1): 71- 80.
doi: 10.1287/ijoc.1090.0327 |
| 32 | 段文睿, 田凌, 韩文彬. 刻蚀机装备设计中的序贯试验设计方法研究[J]. 真空科学与技术学报, 2015, 35 (5): 625- 633. |
| DUAN W R, TIAN L, HAN W B. Analysis of sequential design strategy of etching reactor of 18 inch silicon wafer[J]. Chinese Journal of Vacuum Science and Technology, 2015, 35 (5): 625- 633. | |
| 33 | 孟祥争. 基于K折叠SVR近似模型的晶格结构设计优化方法研究[D]. 武汉: 华中科技大学, 2018. |
| MENG X Z. Research on optimization method of lattice structure design based on K-fold SVR metamodel[D]. Wuhan: Huazhong University of Science and Technology, 2018. | |
| 34 | LIU H T, CAI J F, ONG Y S. An adaptive sampling approach for Kriging metamodeling by maximizing expected prediction error[J]. Computers & Chemical Engineering, 2017, 106, 171- 182. |
| [1] | Yonglin LEI, Yan WANG, Qinzhang YU, Zhi ZHU, Wei DONG, Yifan ZHU. Design method of sequential neighbor exploratory experimental for complex simulation metamodeling [J]. Systems Engineering and Electronics, 2021, 43(5): 1232-1239. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||