近地天体与空间目标初轨确定的多解问题

doi:10.12305/j.issn.1001-506X.2022.09.26

Abstract

Abstract:

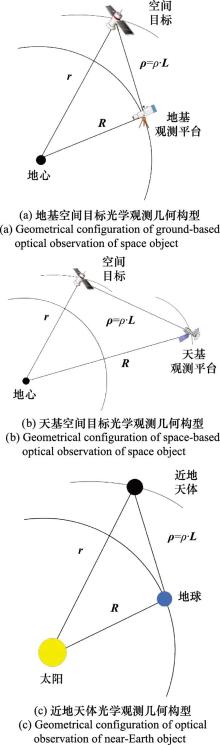
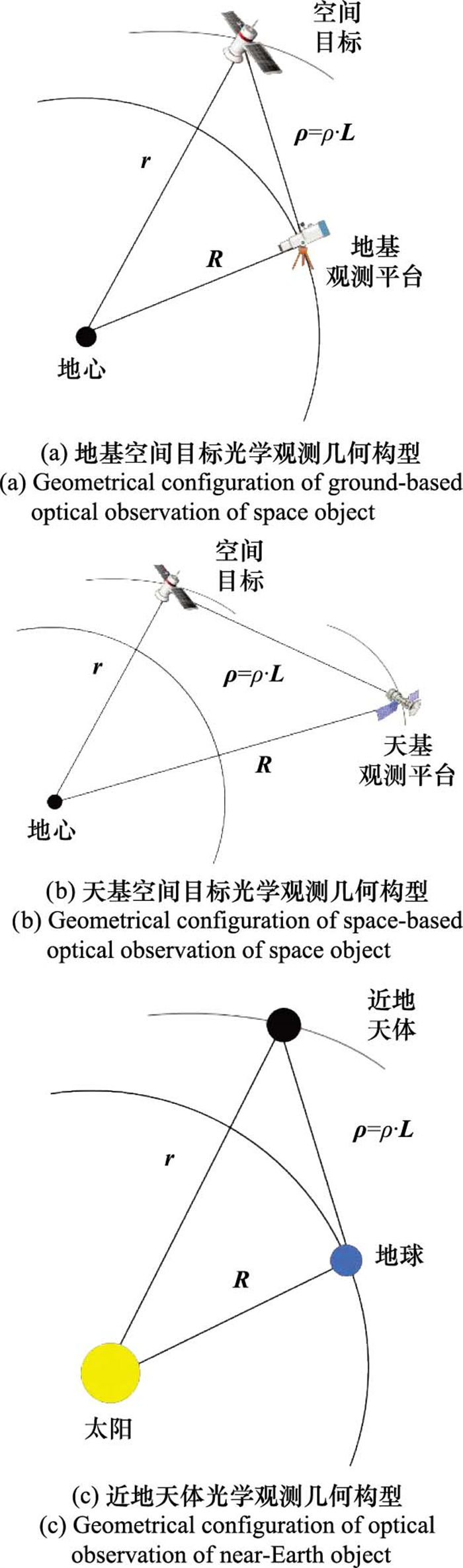
Aiming at the problem that multiple roots cannot be distinguished when solving 8th-degree polynomial equations of Laplace or Gauss form in the process of initial orbit determination (IOD) of near-Earth objects and space objects using optical measurements, this paper proposes an effective distinguishing method. By constructing Laplace form 8th-degree polynomial equation, the relationship between the coefficients of the equation and the number of roots is analyzed. The equation is normalized by using the distance between the observation platform and the geocentric to eliminate the trivial solution and analyze the relationship between the number of non-pseudo solutions and geometrical configuration. Starting from solving the semi-latus rectum, the constraint relationship that the slant range should be satisfied in IOD is derived, using the general equation proposed by Shefer. The analytic form of the equations which should be satisfied between the observation time intervals and the changes of slant range is obtained and the distinguishing method of multi non-pseudo solutions using the equations is given. Finally, the IOD of near-Earth objects and space objects is verified by simulation measurements. The results show that this method can quickly and effectively select the correct root, and solve the problem of multi non-pseudo solutions that cannot be selected.

Key words: initial orbit determination, near-earth object, space target, space-based space target surveillance, 8th-degree polynomial equation

CLC Number:

V412.41

Kexin ZHAO, Qingbo GAN, Zhitao YANG, Jing LIU. Multiple-roots problem of initial orbit determination of near-Earth object and space target[J]. Systems Engineering and Electronics, 2022, 44(9): 2914-2921.

Figures/Tables 11

Fig.1

Fig.2

Fig.3

Fig.4

Table 1

Table 2

Fig.5

Table 3

Table 4

Fig.6

Fig.7

References 30

1	ESCOBAL P R . Methods of orbit determination[M]. Malabar: Krieger, 1976.
2	VALLADO D A . Fundamentals of astrodynamics and applications[M]. 4th ed Hawthorne: Microcosm Press, 2013.
3	GOODING R H. A new procedure for orbit determination based on three lines of sight (angles only), TR 93004[R]. Farnborough: Defence Research Agency Farnborough, 1993.
4	GOODING R H . A new procedure for the solution of the classical problem of minimal orbit determination from three lines of sight[J]. Celestial Mechanics and Dynamical Astronomy, 1996, 66 (4): 387- 423.
5	VALLADO D A. Evaluating gooding angles-only orbit determination of space based space surveillance measurements, USR 10-S4.5[R]. Colorado: Center for Space Standards and Innovation, 2010.
6	KARIMI R R , MORTARI D . Initial orbit determination using multiple observations[J]. Celestial Mechanics & Dynamical Astronomy, 2011, 109 (2): 167- 180.
7	章品, 桑吉章, 潘腾, 等. 应用距离搜索的低轨空间碎片初始轨道确定方法[J]. 航天器工程, 2017, 26 (2): 22- 28. doi: 10.3969/j.issn.1673-8748.2017.02.004
	ZHANG P , SANG J Z , PAN T , et al. Initial orbit determination method based on rang searching for LEO space debris[J]. Spacecraft Engineering, 2017, 26 (2): 22- 28. doi: 10.3969/j.issn.1673-8748.2017.02.004
8	雷祥旭, 桑吉章, 李振伟. LEO空间目标地基甚短弧角度数据初轨确定[J]. 测绘地理信息, 2019, 44 (2): 71- 73.
	LEI X X , SANG J Z , LI Z W . Initial orbit determination with very-short-arc observations of LEO object obtained from ground-based optical telescopes[J]. Journal of Geomatics, 2019, 44 (2): 71- 73.
9	WISHNEK S , HOLZINGER M J , HANDLEY P , et al. Robust initial orbit determination using streaks and admissible regions[J]. Journal of the Astronautical Sciences, 2021, 68, 349- 390. doi: 10.1007/s40295-021-00264-1
10	GRONCHI G F , BAU G , MILANI A . Keplerian integrals, elimination theory and identification of very short arcs in a large database of optical observations[J]. Celestial Mechanics and Dynamical Astronomy, 2017, 127 (2): 211- 232. doi: 10.1007/s10569-016-9725-9
11	GRONCHI G F , BAÙ G , RODRÍGUEZ Ó , et al. Generalization of a method by Mossotti for initial orbit determination[J]. Celestial Mechanics and Dynamical Astronomy, 2021, 133 (9): 1- 21.
12	ANSALONE L , CURTI F . A genetic algorithm for initial orbit determination from a too short arc optical observation[J]. Advances in Space Research, 2013, 52 (3): 477- 489. doi: 10.1016/j.asr.2013.04.004
13	李鑫冉, 赵海斌. 近地小行星极短弧定轨的进化算法研究[J]. 力学学报, 2021, 53 (3): 902- 911.
	LI X R , ZHAO H B . Study on evolutionary algorithms for initial orbit determination of near-earth asteroids with too-short-arc[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53 (3): 902- 911.
14	李鑫冉, 王歆. 基于遗传算法的极短弧定轨[J]. 天文学报, 2016, 57 (1): 66- 77.
	LI X R , WANG X . Genetic algorithm for initial orbit determination with too short arc[J]. Acta Astronomica Sinica, 2016, 57 (1): 66- 77.
15	李鑫冉, 王歆. 基于遗传算法的极短弧定轨(续)[J]. 天文学报, 2016, 57 (2): 181- 187.
	LI X R , WANG X . Genetic algorithm for initial orbit determination with too short arc (continued)[J]. Acta Astronomica Sinica, 2016, 57 (2): 181- 187.
16	LI X R , WANG X , XIONG Y Q . A combination method using evolutionary algorithms in initial orbit determination for too short arc[J]. Advances in Space Research, 2019, 63 (2): 999- 1006. doi: 10.1016/j.asr.2018.08.036
17	HU J , LI B Z , LI J . Initial orbit determination utilizing solution group optimization[J]. IEEE Trans.on Aerospace and Electronic Systems, 2020, 55 (2): 897- 911.
18	HANDLEY P M, HAGERTY S P. Initial orbit determination using simplex fusion[C]//Proc. of the IEEE Aerospace Confe-rence, 2020.
19	CHARLIER C V L . Second note on multiple solutions in the determinationof orbits from three observation[J]. Monthly Notices of the Royal Astronomical Society, 1911, 71, 454- 459. doi: 10.1093/mnras/71.5.454
20	CHARLIER C V L . On multiple solutions in the determination of orbits from three observations[J]. Monthly Notices of the Royal Astronomical Society, 1910, 71, 120- 124. doi: 10.1093/mnras/71.2.120
21	DANBY J M A . Fundamentals of celestial mechanics, the macmillan company[M]. New York: Macmillan Collection, 1962.
22	GRONCHI G F . Multiple solutions in preliminary orbit determination from three observations[J]. Celestial Mechanics & Dynamical Astronomy, 2009, 103 (4): 301- 326.
23	DER G. New angles-only algorithms for initial orbit determination[C]//Proc. of the Advanced Maui Optical and Space Surveillance Technologies Conference, 2012: 412-427.
24	WIE B , AHN J . On selecting the correct root of angles-only initial orbit determination equations of Lagrange, Laplace, and Gauss[J]. The Journal of the Astronautical Sciences, 2017, 64, 50- 71. doi: 10.1007/s40295-016-0097-x
25	PRUSSING J E , CONWAY B A . Orbital mechanics[M]. New York: Oxford University Press, 1993.
26	甘庆波, 马静远, 陆本魁, 等. 一种基于星间方向观测的初轨计算方法[J]. 宇航学报, 2008, 28 (3): 619- 622.
	GAN Q B , MA J Y , LU B K , et al. An initial orbit determination method using inter satellite angle measurement[J]. Journal of Astronautics, 2008, 28 (3): 619- 622.
27	KUZNETSOV V B . Revisiting the determination of a preliminary orbit for a celestial body[J]. Solar System Research, 2019, 53 (6): 462- 472. doi: 10.1134/S0038094619060054
28	SHEFER V A . New method of orbit determination from two position vectors based on solving Gauss's equations[J]. Solar System Research, 2010, 44 (3): 252- 266. doi: 10.1134/S003809461003007X
29	KARIMI R R, MORTARI D. On Laplace's orbit determination method: some modifications[C]//Proc. of the AAS/AIAA Space Flight Mechanics Meeting, 2011.
30	BINI D A . Numerical computation of polynomial zeros by means of Aberth's method[J]. Numerical Algorithms, 1996, 13 (2): 179- 200. doi: 10.1007/BF02207694

观测时刻	MJD	赤经/(°)	赤纬/(°)	地球X/AU	地球Y/AU	地球Z/AU
t₁	59 243.266 710	47.719 328	17.782 398	-0.616 715 716	0.704 510 08	0.305 402 78
t₂	59 253.277 130	37.983 650	14.938 175	-0.743 577 968	0.594 637 62	0.257 776 60
t₃	59 264.183 290	27.591 571	11.353 189	-0.855 605 760	0.454 102 59	0.196 856 38

正实根	ρ₁	ρ₂	ρ₃
1	-1.073 154 12	-0.948 024 74	-0.779 208 16
2	0.170 215 00	0.145 732 50	0.124 410 83

观测时刻	MJD	赤经/(°)	赤纬/(°)	观测平台X/km	观测平台Y/km	观测平台Z/km
t₁	59 410.192 361 11	14.412 735	-32.412 455	-6 323.548	-2 290.293	547.849
t₂	59 410.194 444 44	12.478 481	-29.897 754	-5 779.067	-3 482.275	115.328
t₃	59 410.196 527 78	12.891 181	-26.900 668	-4 992.551	-4 528.415	-322.023

非伪解	ρ₁/R_Earth	ρ₂/R_Earth	ρ₃/R_Earth	f₁	f₃
1	0.777 383 57	0.588 538 89	0.444 578 59	0.007 445 23	0.005 868 73
2	4.647 871 44	3.459 195 58	2.658 074 77	1.634 331 24	1.653 806 37

[1]	Dawei LI, Jing LIU, Xiyan PENG, Yao ZHANG, Yanhao XIE. Initial orbit determination for a near-circular orbit of space debris with space-based short-arcs method and experiment [J]. Systems Engineering and Electronics, 2022, 44(8): 2601-2611.
[2]	Tao JIN, Di ZHU, Jieying HE, Wenyu WANG. Study on the characteristics of high terahertz band atmospheric background radiation observed from satellites [J]. Systems Engineering and Electronics, 2022, 44(10): 3003-3011.
[3]	ZHAO Huipeng, WANG Junling, GAO Meiguo, GUO Baofeng, MA Shaochuang. Bistatic ISAR envelope alignment algorithm based on orbit error search [J]. Systems Engineering and Electronics, 2017, 39(6): 1235-1243.
[4]	YU Xiang, ZHU Daiyin, LI Junqiang, YUN Tao, HUANG Xiangfei. Range alignment algorithm based on the range migration trajectory for the space target ISAR [J]. Systems Engineering and Electronics, 2017, 39(4): 775-781.
[5]	GUO Baofeng1,2, SHANG Chao-xuan1, WANG Jun-ling2, GAO Mei-guo2. Bistatic ISAR echo simulation of space target based on twobody model [J]. Systems Engineering and Electronics, 2016, 38(8): 1771-1779.
[6]	ZHU Jiang, LIAO Gui-sheng, ZHU Sheng-qi. High precision range compression based on FrFT for space target imaging [J]. Systems Engineering and Electronics, 2015, 37(2): 271-277.
[7]	ZHANG Jian, XI Xiao-liang, ZHOU Xiao-dong. Space target detection in star image based on motion information [J]. Systems Engineering and Electronics, 2014, 36(5): 838-845.
[8]	DENG Xiao-bo，SHI Chang-hai，GAO Chao，YANG Jian. Subspace signal detection in compound Gaussian clutter [J]. Systems Engineering and Electronics, 2013, 35(9): 1836-1840.
[9]	JIANG Wei-dong, CAO Min, NIE Lei, FU Yao-wen. Study on dynamic electromagnetic data simulation of space targets [J]. Journal of Systems Engineering and Electronics, 2009, 31(9): 2042-2045.
[10]	YE You-shi, TANG Lin-bo, ZHAO Bao-jun, CAI Xiao-fang. Realtime deep space target track system based on SOPC [J]. Journal of Systems Engineering and Electronics, 2009, 31(12): 3002-3006.

Multiple-roots problem of initial orbit determination of near-Earth object and space target

RichHTML

PDF (PC)

Knowledge

Abstract

Cite this article

share this article

Figures/Tables 11

References 30

Related Articles 10

Recommended Articles

Metrics

Comments