0 引言
随着科学技术的发展, 航天、航空、航海、轨道交通、汽车等领域对电气系统的需求日益提升[1-4]。为提高工作可靠度, 针对电气系统的可靠性冗余设计获得越来越多的重视[5-6]。可靠性冗余设计作为提高复杂系统可靠性的一种重要手段, 其目标是通过增加系统单元的冗余数量来提高系统整体的可靠度。但是,单元冗余数量的增加,必然会导致系统费用、体积、质量和功耗等要素升高, 导致系统工作效率、维护成本等增加, 因此可靠性冗余设计必须综合考虑系统对可靠性、费用、体积、质量和功耗等要素的不同要求, 设计同时满足可靠性、费用等不同要素要求的产品。根据优化目标差异, 可靠性冗余设计通常可以分为两类[7]: ①以系统费用、体积、质量和功耗等为约束, 正确配置各子系统单元, 使电气系统可靠性达到最大; ②以电气系统可靠度指标为约束, 正确配置各子系统单元, 使系统费用、体积、质量和功耗等最少。
针对上述问题, 本文根据单元协同平衡原理, 探索了基于子系统冗余单元协同平衡的电气系统可靠性冗余设计多目标优化算法, 通过充分考虑冗余单元变化对复杂系统可靠度、费用、体积、质量和功耗等性能参数的影响, 可以有效解决各类可靠性冗余设计优化问题。本文引言部分介绍了本文的研究背景和现状, 提出本文研究目标; 第1节系统介绍了可靠性冗余系统模型和优化模型; 第2节介绍了基于单元协同平衡的优化原理及其计算流程; 第3节通过桥式冗余系统和串-并联系统两种可靠性模型的比较, 研究了基于单元协同平衡优化算法的有效性与准确性; 第4节采用基于单元协同平衡的冗余设计优化算法对运载火箭中的压力控制继电器单机可靠性进行优化设计, 为提升系统可靠性提供参考。
1 冗余系统
设电气系统X={x1, x2, …, xi, …, xn}是n个冗余子系统的集合, x1, x2, xi和xn分别是第1, 2, i和第n个子系统中的单元数量, i={1, 2, …, n}。可知, 系统可靠度Rs是与各子系统可靠度相关的函数, 记为
式中: Rs是可靠性冗余系统的可靠度; R(xi)是第i个子系统的可靠度; FR表明Rs是与R(xi)相关的映射函数。根据电气系统各子系统串、并联组成系统的可靠性模型差异, 函数FR亦存在差别。由于子系统的冗余设计通常由多个单元并联实现, 可得
式中: ri是第i个子系统中冗余单元的可靠度。
同理, 可靠性冗余系统费用、体积、质量、功耗也是与单元费用、单元体积、单元质量、单元功耗以及单元数量相关的函数, 其计算表达式可分别写为
式中: Cs是可靠性冗余系统的系统费用; Ci是第i个子系统中每个单元的费用; Vs是可靠性冗余系统的系统体积; Vi是第i个子系统中每个单元的体积; Ws是可靠性冗余系统的系统质量; Wi是第i个子系统中每个单元的质量; Ps是可靠性冗余系统的系统功耗; Pi是第i个子系统中每个单元的功耗; FC, FV, FW, FP分别是系统费用、系统体积、系统质量、系统功耗的函数。
根据优化目标的差异, 可靠性冗余设计优化可以分为以下两类。
(1) 以电气系统最高费用、最高体积、最高质量或最高功耗为约束, 正确配置各子系统单元, 使系统可靠性达到最大, 其优化模型的计算表达式为
式中: C0、V0、W0和P0分别是系统最高成本、系统体积、系统质量和系统功耗约束。
(2) 以电气系统最低可靠度指标为约束, 正确配置各子系统单元, 使系统费用、系统体积、系统质量和系统功耗等最少,其优化模型的计算表达式为
式中: R0是系统最低可靠度约束。
2 优化算法
2.1 定义
平衡态: 可靠性系统满足约束条件的一种解。
平衡优化: 可靠性系统从一个非平衡态(无解)转换到下一个平衡态(有解), 或者从一个平衡态(有解)转换至下一个更优的平衡态的过程。
优化判据: 平衡优化的依据, 具体指系统可靠度满足设计要求时, 系统成本、体积、质量或功耗降低; 或系统费用、体积、质量或功耗满足设计要求时, 系统可靠度升高。
2.2 优化原理
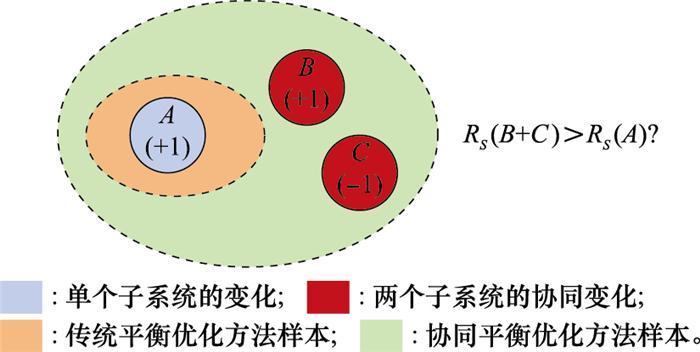
基于协同平衡的可靠性冗余设计优化算法在完成每一次优化迭代分析时,允许多个子系统中的单元同时发生状态变化, 以1个单元数作为变量, 每个子系统存在增加(+1)、减少(-1)和保持不变(+0)3种状态变化。可知, 在每一次优化迭代中, 系统共存在3n种变化, 其中既包含由单个子系统单元数量的变化产生的新状态, 还包含两个或多个子系统协同增、减产生的新状态。
采用传统平衡优化算法求解第一类可靠性冗余设计优化问题时, 主要通过在子系统并联多个单元的方式实现系统可靠性的提升。每一次优化迭代都是在各子系统中选择系统可靠性提升最多的子系统增加新的单元, 可以产生n种新状态变化。采用基于协同平衡的可靠性冗余设计优化算法求解上述问题, 每一次优化迭代则可以产生3n种新状态变化, 这其中不但包括单个子系统增加产生的新状态, 还包括两个或两个以上子系统协同变化所产生的新状态变化, 如图 1所示。同时, 上述新状态变化数量同样符合第二类可靠性冗余设计优化问题。
图1
图1
协同平衡优化算法示意图
Fig.1
Schematic diagram of collaborative balance optimization algorithm
当n>1时, 3n>n始终成立。可见, 初始平衡态相同的条件下, 基于协同平衡的可靠性冗余设计优化算法单次优化迭代可以产生更多的状态变化, 进而可以实现传统平衡可靠性冗余设计优化结果的进一步提升。
2.3 算法流程
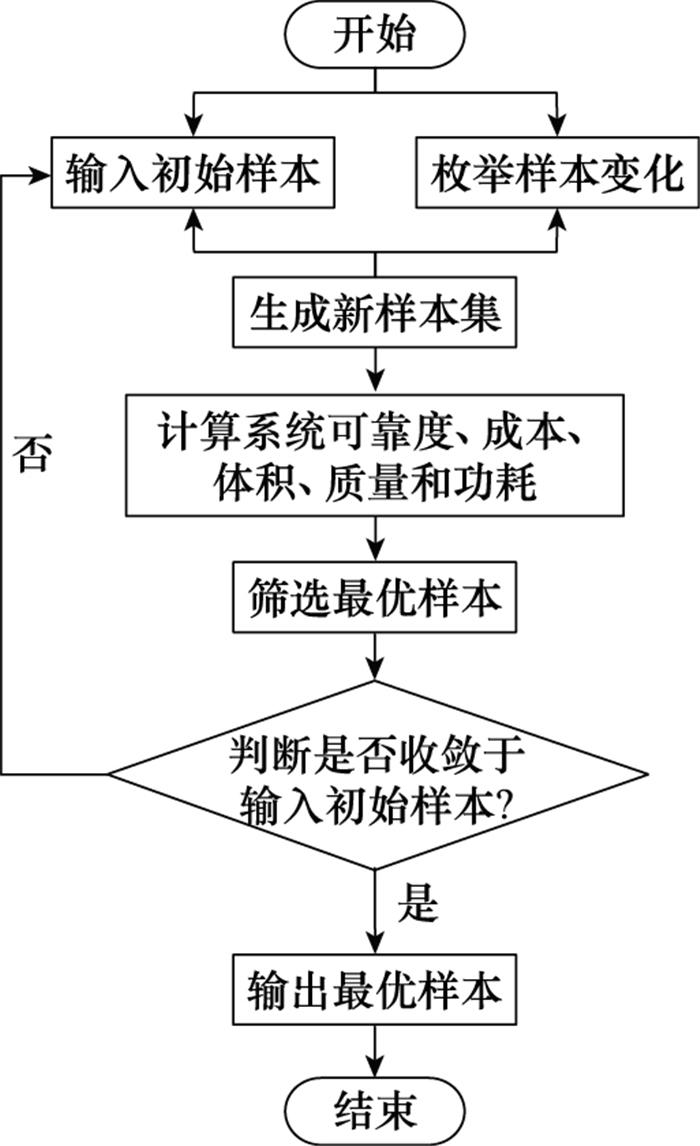
基于协同平衡的可靠性冗余设计优化算法实现流程如图 2所示, 具体实施步骤如下。
图2
步骤1 提出初始平衡样本。算法要求初始样本应该在完成第一轮计算后成为冗余系统的可行解, 初始样本亦可以随机给出, 但要求在第一轮计算后应成为平衡态可行解。为提升计算效率, 输入初始样本还可以通过计算确定, 具体计算方法为: ①在成本、体积、质量或功耗要求范围内求解可靠度最高的平衡状态样本时, 假定各子系统成本、体积、质量相同, 求解满足成本、体积、质量或功耗要求的各子系统的单元数量;②在可靠度要求范围内求解最优成本、体积、质量以及功耗设计时, 假定各子系统可靠度相同, 求解满足可靠度要求的各子系统单元数量。
步骤2 构造平衡态样本变化数据集。按照增加、减少和保持不变3种状态枚举平衡状态变化量, 构造样本变化数据集, 如表 1所示。
表1 样本变化数据集
Table 1
| 样本序号 | 第1个子系统 | 第2个子系统 | … | 第i个子系统 | … | 第n个子系统 |
| 第1种 | -1 | -1 | … | -1 | … | -1 |
| 第2种 | -1 | -1 | … | -1 | … | 0 |
| 第3种 | -1 | -1 | … | -1 | … | 1 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 第3n-2种 | 1 | 1 | … | 1 | … | -1 |
| 第3n-1种 | 1 | 1 | … | 1 | … | 0 |
| 第3n种 | 1 | 1 | … | 1 | … | 1 |
步骤3 生成新样本集。根据样本变化, 计算新的样本集, 其计算表达式为
式中:
步骤4 计算冗余系统可靠度、成本、体积和质量。根据式(1)~式(6)计算由每种新样本数据构造的可靠性系统的可靠度、成本、体积、质量以及功耗。
步骤5 筛选最优样本。根据式(7)和式(8)中的优化目标对新样本数据进行筛选, 保留非0的平衡态样本, 并从中选出满足目标函数要求的最优平衡态样本。
步骤6 完成最优样本判定, 并输出最优样本。比较筛选的最优平衡态样本以及输入的初始样本, 两者相等表明算法收敛, 计算系统可靠性、成本、质量和体积等数据,并输出最优平衡态样本结果。
3 算例验证
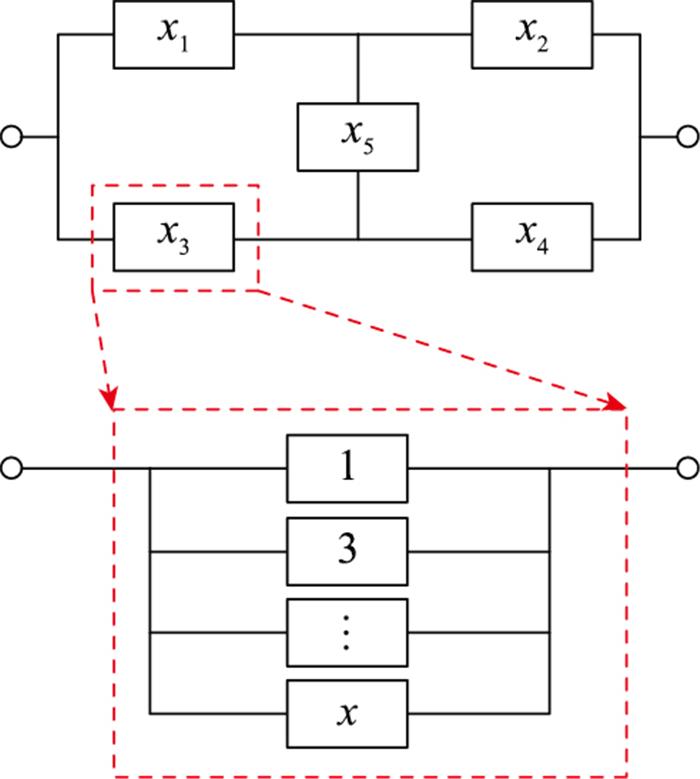
3.1 桥式冗余系统
图3
算例中各子系统冗余单元参数如表 2所示, 通过协同平衡优化法求解上述算例的最优设计结果, 可知在电气系统可靠性约束条件下, 采用协同平衡优化算法设计的可靠性系统各单元数量与平衡优化算法设计的可靠性系统各单元数量均为1, 2, 3, 1, 2, 满足系统可靠度高于0.99的设计要求, 同时系统费用为19, 如表 3所示。采用一般平衡优化算法求解相同的冗余优化问题, 针对相同初始平衡样本(3, 2, 2, 2, 2)的优化结果为3, 2, 2, 1, 1, 系统可靠度和费用分别为0.993 2和20。通过对比可知, 在满足系统可靠度大于0.99的条件下, 本文协同平衡优化算法的优化结果所需系统费用更低。
表2 桥式可靠性系统冗余单元可靠性及费用
Table 2
| 参数 | 子系统 | ||||
| i=1 | i=2 | i=3 | i=4 | i=5 | |
| 单元可靠性 | 0.70 | 0.85 | 0.75 | 0.80 | 0.90 |
| 单元费用 | 2 | 3 | 2 | 3 | 1 |
表3 桥式可靠性系统冗余设计优化结果对比
Table 3
| 计算算法 | 初始冗余数 | 优化冗余数 | 系统可靠度 | 系统费用/元 |
| 一般平衡优化算法[24] | 3, 2, 2, 2, 2 | 3, 2, 2, 1, 1 | 0.993 2 | 20 |
| 协同平衡优化算法 | 3, 2, 2, 2, 2 | 1, 2, 3, 1, 2 | 0.990 3 | 19 |
| 1, 1, 1, 1, 1 | 1, 2, 3, 1, 2 | 0.990 3 | 19 | |
| 5, 5, 5, 5, 5 | 1, 2, 3, 1, 2 | 0.990 3 | 19 |
协同优化算法还可以采用随机初始样本进行求解, 例如, 随机初始样本(1, 1, 1, 1, 1)和(5, 5, 5, 5, 5)作为输入计算的优化结果与采用可行解计算的优化结果相同, 表明本文协同优化算法还可以采用随机初始样本进行优化设计。此外, 该算法的迭代计算次数通常在10以内, 计算效率优于一般智能算法。
3.2 串-并联冗余系统
图4
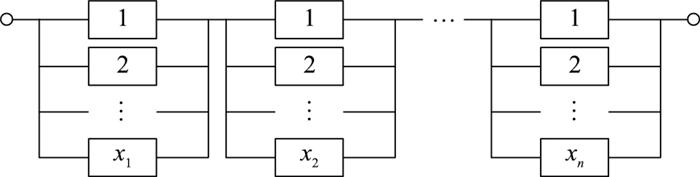
图4
复杂串-并联可靠性系统框图
Fig.4
Block diagram of the complex series-parallel reliability system
式中: C0、V0和W0分别是系统最高成本、体积、质量和功耗约束, 如表 4所示。
表4 串-并联可靠性模型参数
Table 4
| i | ri | ci | C0 | pi | P0 | wi | W0 |
| 1 | 0.80 | 7 | 175 | 1 | 110 | 7 | 200 |
| 2 | 0.85 | 7 | 175 | 2 | 110 | 8 | 200 |
| 3 | 0.90 | 5 | 175 | 3 | 110 | 8 | 200 |
| 4 | 0.65 | 9 | 175 | 4 | 110 | 6 | 200 |
| 5 | 0.75 | 4 | 175 | 2 | 110 | 9 | 200 |
采用协同平衡优化法求解上述算例的最优结果, 并与一阶领域启发式遗传算法、一阶领域启发式遗传算法与粒子群优化算法的联合算法的计算结果进行对比。在电气系统成本、体积和质量约束条件下, 采用协同平衡优化算法设计的可靠性系统可靠度为0.933 1, 采用一阶领域启发式遗传算法和联合算法设计的可靠性系统可靠度为0.904 5, 采用本文协同平衡优化算法设计的复杂串-并联系统可靠度为0.933 1, 可靠度提升了0.028 6, 如表 5所示。
表5 串-并联系统优化结果对比
Table 5
4 工程应用
运载火箭压力控制继电器组合是其增压输送系统的核心部件, 采用冗余设计优化算法提升其系统可靠性十分必要。
图5
图5
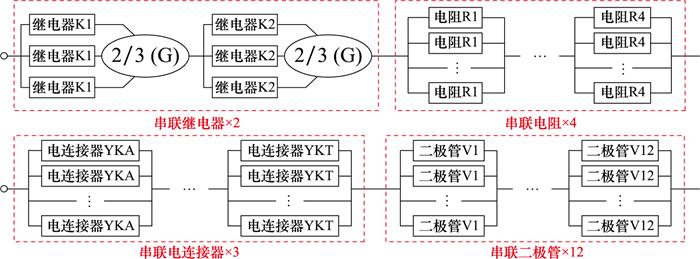
压力控制继电器组合可靠性框图
Fig.5
Reliability diagram of the pressure-controlled relay combination
表6 压力控制继电器组合元器件参数
Table 6
| 序号 | 元器件 | 单元失效率(10-6/h) | 单元可靠度 | 费用/元 |
| 1 | 继电器 | 5.351 00 | 0.999 987 2 | 8.00 |
| 2 | 电阻 | 0.008 18 | 0.999 999 9 | 0.36 |
| 3 | 二极管 | 0.084 90 | 0.999 999 8 | 1.25 |
| 4 | 电连接器 | 0.059 00 | 0.999 999 9 | 1.20 |
初始状态下,压力控制继电器组合中的继电器、电阻、二极管和电连接器各单机数量分别为(3, 3)、(2, 2, 1, 1)、(2, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1)、(1, 1, 1),系统初始可靠度为0.999 997 9,系统初始费用为73.76元。
采用协同平衡优化法对继电器、电阻、二极管和电连接器进行冗余设计优化,可得压力继电器组合中继电器、电阻、二极管、电连接器子系统中冗余单元数量分别为(2, 2)、(1, 1, 1, 1)、(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)、(1, 1, 1),继电器组合飞行可靠性仍然满足可靠性设计要求。此时,系统优化可靠度是0.999 997 1,系统优化费用是52.04元,冗余量优化结果如表 7所示。在系统可靠性满足要求的前提下,系统费用降低了29.45%,实现了系统优化目标。
表7 压力控制继电器组合飞行可靠性优化结果
Table 7
| 序号 | 子系统 | 初始冗余数量 | 优化冗余数量 |
| 1 | 继电器K1 | 3 | 2 |
| 2 | 继电器K2 | 3 | 2 |
| 3 | 电阻R1 | 2 | 1 |
| 4 | 电阻R2 | 2 | 1 |
| 5 | 电阻R3 | 1 | 1 |
| 6 | 电阻R4 | 1 | 1 |
| 7 | 二极管V1 | 2 | 1 |
| 8 | 二极管V2 | 2 | 1 |
| 9 | 二极管V3 | 2 | 1 |
| 10 | 二极管V4 | 2 | 1 |
| 11 | 二极管V5 | 1 | 1 |
| 12 | 二极管V6 | 1 | 1 |
| 13 | 二极管V7 | 1 | 1 |
| 14 | 二极管V8 | 1 | 1 |
| 15 | 二极管V9 | 1 | 1 |
| 16 | 二极管V10 | 1 | 1 |
| 17 | 二极管V11 | 1 | 1 |
| 18 | 二极管V12 | 1 | 1 |
| 19 | 电连接器YKA | 1 | 1 |
| 20 | 电连接器YKP | 1 | 1 |
| 21 | 电连接器YKT | 1 | 1 |
5 结论
传统冗余设计优化算法仅考虑单个单元变化对可靠性系统的影响, 而忽略了单元协同变化对系统可靠度的影响。针对上述问题, 本文根据各子系统单元协同平衡的原理, 提出了电气系统可靠性冗余设计协同优化算法。该算法充分考虑冗余单元协同变化对复杂系统可靠度、费用、体积、质量和功耗等性能参数的影响, 可以有效解决串-并联系统的可靠性设计优化。
算例结果表明, 基于协同平衡的可靠性冗余设计算法即可在可靠性约束条件下对系统费用、体积、质量或功耗等要素进行优化, 亦可在系统费用、体积、质量或功耗等约束条件下对系统可靠性进行优化。例如, 将桥式冗余系统的费用降低至19或者将串-并联冗余系统的可靠度提升0.028 6。此外, 在工程应用算例中, 借助本文协同优化算法,可以降低运载火箭压力控制继电器组合的系统费用, 在确保可靠性指标满足设计要求的前提下,可使系统费用降低29.45%, 实现了系统优化目标。
参考文献
Life-cycle reliability-based optimization of civil and aerospace structures
[J].DOI:10.1016/S0045-7949(03)00020-8 [本文引用: 1]
Reliability for aerospace systems: methods and applications
[J].
Reviews and challenges in reliability design of long march launcher control systems
[J].DOI:10.2514/1.J060640 [本文引用: 1]
Launch vehicle multi-objective reliability-redundancy optimization using a hybrid genetic algorithm-particle swarm optimization
[J].DOI:10.1177/0954410014560381 [本文引用: 1]
An efficient heuristic for reliability design optimization problems
[J].DOI:10.1016/j.cor.2009.04.011 [本文引用: 1]
An improved algorithm for reliability optimization
[J].
Redundancy optimization in general systems
[J].
A cuckoo search algorithm by Lévy flights for solving reliability redundancy allocation problems
[J].DOI:10.1080/0305215X.2012.729055
Novel general active reliability redundancy allocation problems and algorithm
[J].DOI:10.1016/j.ress.2021.108167 [本文引用: 1]
Multiobjective optimization by genetic algorithms: application to safety systems
[J].DOI:10.1016/S0951-8320(00)00109-5 [本文引用: 1]
Alternatives and challenges in optimizing industrial safety using genetic algorithms
[J].DOI:10.1016/j.ress.2003.12.010
Multi-objective optimization of reliability-redundancy allocation problem with cold-standby strategy using NSGA-Ⅱ
[J].DOI:10.1016/j.ress.2017.12.019 [本文引用: 1]
可靠性冗余优化设计算法研究
[J].
Research of algorithm for reliability redundancy optimization design
[J].
An efficient particle swarm approach for mixed-integer programming in reliability-redundancy optimization applications
[J].DOI:10.1016/j.ress.2008.09.001
An improved particle swarm optimization algorithm for reliability problems
[J].DOI:10.1016/j.isatra.2010.08.005 [本文引用: 1]
New methods to minimize the preventive maintenance cost of series-parallel systems using ant colony optimization
[J].DOI:10.1016/j.ress.2004.09.005 [本文引用: 1]
基于仿真的复杂系统可靠性冗余分配优化设计
[J].
Redundancy allocation optimization design for complex system based on simulation
[J].
Multi-objective optimization of reliability-redundancy allocation problem for multi-type production systems considering redundancy strategies
[J].DOI:10.1016/j.ress.2019.106681 [本文引用: 1]
Multi-objective evolutionary algorithm on reliability redundancy allocation with interval alternatives for system parameters
[J].DOI:10.1007/s00521-022-07459-z [本文引用: 1]
A new heuristic algorithm for constrained redundancy optimization in complex systems
[J].
复杂系统可靠性冗余的平衡优化方法
[J].
Balance method of optimal redundancy in complex systems
[J].
冗余系统费用模型及优化
[J].
Cost models and optimization of redundant system
[J].
A novel evolutionary algorithmic solution approach for bilevel reliability-redundancy allocation problem
[J].