0 引言
在现代空战中, 战术机动是战斗机躲避雷达探测和导弹拦截的重要手段, 因此战术机动飞行训练逐渐成为了飞行员日常训练的一项核心内容。对战术机动的飞行质量进行具体评估是战术机动飞行训练的一个重要环节, 其对提升飞行员的操作能力和作战水平而言意义重大。在传统评估方法中, 由于飞行员对飞行教官的判断有着严重依赖, 存在着效率低下、主观性强等问题, 已经不能满足现代飞行训练的要求。为此, 实现飞行训练质量的自动化快速评估, 具有重要的军事价值和实际意义。
飞行训练质量自动化评估包含两方面内容: 一是战术机动动作的识别; 二是基于识别结果的战术机动飞行过程质量评估。目前, 国内外学者已经在这两个问题上进行了一些研究。在战术机动识别方面, 杨俊等[1]将模糊逻辑理论和支持向量机相结合, 在多分类问题上取得了较好的效果。Tian等[2]基于模糊控制理论, 利用标记数据节点、去除扰动、特征提取等方法解决机动动作识别不准确、延迟高等问题。但是, 模糊理论依赖相关专家对机动特征的准确判断, 识别结果不够客观, 小规模样本集的训练也容易造成训练精度差的问题。徐西蒙等[3]采用运动分解和层次支持向量机的方法, 利用二分类器构造多分类器, 提高准确性和识别效率。Yang等[4]建立层次识别模型, 通过级联结构降低计算复杂度, 克服了当样本数量较多时的收敛性和实时性较差的问题。上述方法将复杂轨迹分解为简单轨迹, 虽然简化了识别过程, 但由于复杂机动与简单机动在机动动作中的飞行参数有着很大差异, 导致在复杂战术机动动作的识别问题中表现不佳。Wei等[5]将机动识别看作多维时间序列的时空对齐问题, 提出了一种多策略的正则仿射时间翘曲方法, 在时间序列分类数据集和无人机机动实验上取得了较好的效果。然而, 在空战对抗背景下进行敌机机动识别, 部分飞行参数难以通过探测手段获取[3-5]。
在飞行训练质量评估方面, 张建业等[6]依据飞行数据和专家经验, 建立飞行成绩自动评定及管理系统, 能够准确快速地评定飞行成绩。Long等[7]提出了基于模糊逻辑理论的飞行质量评估模型, 在模拟飞行机动的进近段中评估结果和实际得分几乎一致。但是传统评估方法过于依赖人的主观判断, 评估方法不够科学, 并且成本较高、效率低下[6-7]。柳忠起等[8]利用眼动数据构建反向传播(back propagation, BP)神经网络, 实现了3种技术水平飞行员的飞行绩效准确评估。姚裕盛等[9]基于飞行员生理信号和飞行参数, 建立了基于BP神经网络的评估模型, 评估结果与专家评分大致吻合。刘浩等[10]使用动态贝叶斯网络识别机动动作, 建立灰度模糊评估矩阵进行飞行质量评估, 提升了飞行训练评估效率。但是浅层学习模型只能提取数据的浅层特征, 缺少语义信息, 模型表达能力不强, 评估结果不稳定[8-10]。此外, 现有的大多数评估方法主要是对飞行训练后的数据进行质量评估, 但是在飞行训练过程中, 不同种类的战术机动动作对应的有效评估指标有所不同, 因此缺乏对不同种类战术机动动作的具体评估。
本文的贡献主要有以下几点: ①针对战术机动识别中的准确度和实时性不高的问题, 采用多尺度特征融合的深度神经网络构建分类器, 通过对飞行参数的多维度深层特征提取实现对不同种类战术机动的识别, 这样既减少了网络深度, 提升识别效率, 又能充分获取不同尺度数据信息, 以保证准确度; ②针对不同战术机动动作类型的有效评估指标不同的问题, 搭建飞行质量评估指标体系, 建立评估指标标准, 将评估过程定量化, 使得评估结果更加客观准确; ③针对不同指标之间存在的差异, 使用基于博弈论的组合赋权方法消除了单一主观或客观评价对评估结果的不利影响, 得到不同战术机动动作所对应的有效评估指标权重, 最终得到评估结果。所提出的飞行训练质量自动评估方法可以有效降低训练成本, 提升效率, 满足现代飞行训练的要求。
需要说明的是, 战斗机可执行的战术机动动作类型多达几十种。为简便起见, 在本文中, 选取斤斗、斜斤斗、半滚倒转、半斤斗翻转4个基本动作, 以及半滚倒转-斤斗, 半滚倒转-半斤斗翻转两个组合动作(共计6个动作类型)作为需要进行机动识别和飞行质量评估的典型战术动作类型。
1 战术机动动作识别
准确识别战术机动动作是进行飞行质量评估的基本前提。在战术机动过程中, 飞行参数也会不断变化, 参数主要包括位置、速度、加速度、航向角、俯仰角、滚转角等信息[11], 不同的战术机动动作对应的飞行参数变化规律也不同。本文针对离线数据进行识别, 飞行参数序列完整, 由于战术机动种类不同, 可以将此类识别问题归结为多分类问题。目前, 处理多分类问题常用的方法就是机器学习[12-13]。机器学习是一种数据驱动的识别方法, 在非线性问题上的处理能力十分强大, 能够通过内部参数的不断调整来获取数据中的特征信息, 也就是机器在不断学习进化的过程。相比传统的识别方法, 机器学习无需先验知识, 识别结果更加快速准确。
Sun等[14]将过去机器学习取得的成功主要归功于更加复杂的网络结构, 更大规模的标签数据集以及更强大的计算性能。在机器学习中, 对数据进行一维卷积处理相较于对图片、视频等进行二维或三维卷积处理要简单很多, 因此无需太复杂的网络, 即可取得较好的效果。为了保持网络精度, 降低计算复杂度, 设计轻量化的网络模型十分必要。因此, 本文中战术机动识别的主要方法就是搭建合适的轻量化网络和建立完备的数据集。
1.1 网络模型介绍
1.1.1 深度残差网络模块
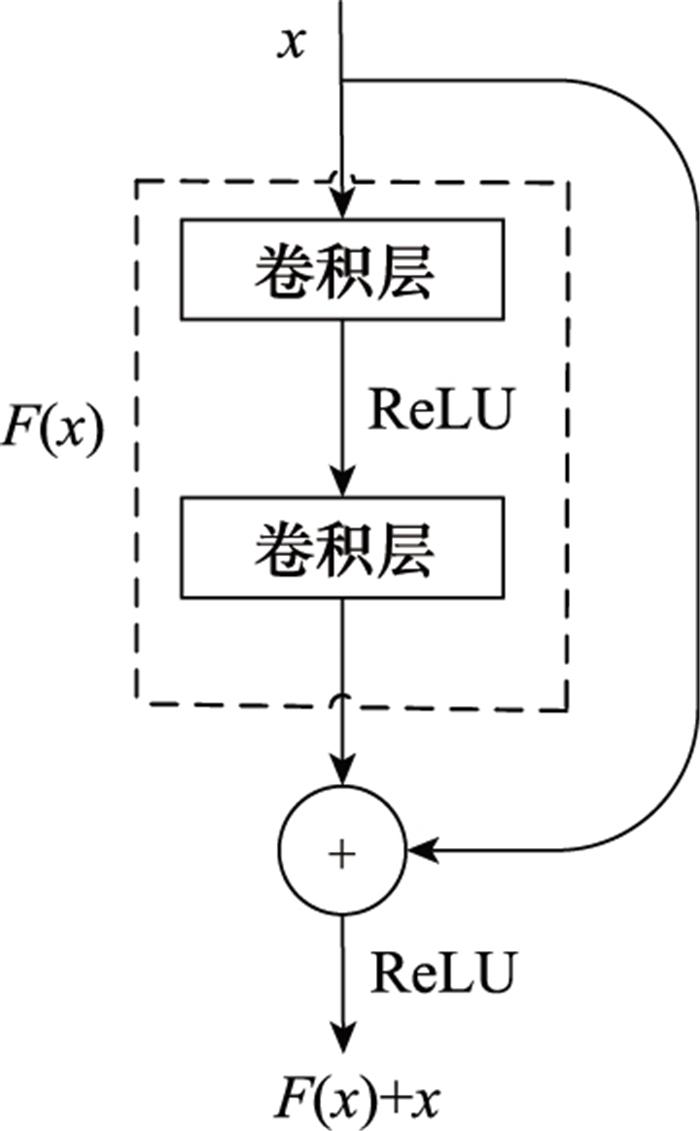
图1
残差模块的输出是模块的输入和经过卷积计算后的期望输出相加的结果, 恒等映射的作用就是始终输出一个权值为1的梯度, 这样就不会随着网络的加深而出现梯度消失的现象, 同时也不会过多地增加网络的参数和计算量。计算表达式为
通常情况下, 在ResNet34及以下的浅层网络中使用图 1中的结构, 在更深层的残差网络中, 如ResNet101, 会将两层卷积替换为3层卷积, 其中包括两个1×1卷积, 用于将网络进行降维和升维处理。相比直接堆叠浅层网络的残差模块, 这样会将参数数量大幅缩减, 从而大幅提升网络的训练效率。
1.1.2 多尺度特征提取
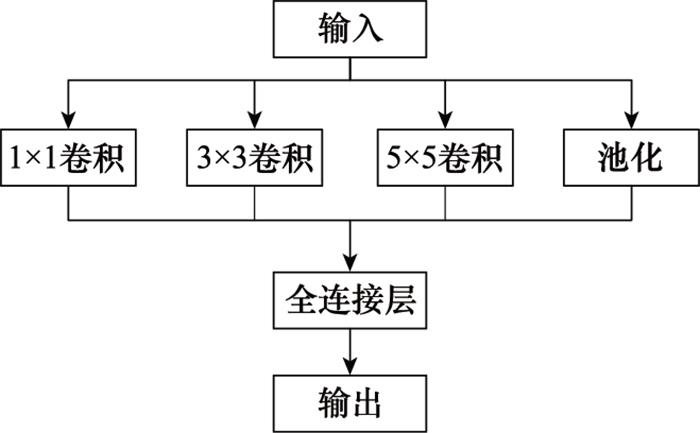
战术机动过程中的飞行参数信息具有明显的非线性、非平稳特征, 尽管目前ResNet已被广泛地运用到了分类识别领域, 但通常是通过堆叠网络层数以取得更好的效果, Wu等[20]研究发现, 特定网络只有在有效深度内才会通过加深层数显著提升精度, 网络的宽度对结果的影响也十分重要。单一的网络通路结构不能同时提取出不同尺度数据内的特征信息, 限制了分类性能。因此, 对数据进行不同尺度卷积的特征提取就显得十分必要, 使用多尺度特征提取来获得不同尺度下的数据特征可以有效地提升分类的准确性。
图2
1.1.3 网络模型
为了兼顾残差网络和多尺度特征提取的优势, 将残差模块和多尺度特征提取的结构相结合, 构建多尺度特征提取的深度残差网络(multi-scale feature extraction deep residual network, MSDRN)模型, 如图 3所示。网络的输入是大小为1×H的一维数据, 其中H为特征个数。首先将输入通过一个卷积层提高通道数以提升网络的学习性; 然后通过一个批标准化、激活函数以及最大池化的串行结构, 完成浅层特征提取, 之后将其接入到网络主体中。网络主体由3个并行支路组成, 每条支路卷积层的尺寸大小不同, 对应的感受野范围也就不同, 因此可以获取到数据中不同尺度的特征信息, 构成多尺度特征提取模块。奇数尺寸的滤波器可以提取出更好的中心特征, 所以均采用了奇数大小的卷积核, 同时小尺寸的卷积核相较于大尺寸卷积核更有利于压缩网络规模。如图 3所示, 3条支路分别由1×1、1×3、1×5大小的残差模块串联组合而成。在每条支路的末端, 通过一个平均池化层降低参数量, 并确保3条支路的输出维度一致。在网络的最后, 使用全连接层增强模型的非线性并输出结果。以其中一条支路为例, 模型中参数大小如表 1所示。
图3
表1 模型参数大小
Table 1
| 模块名称 | 输出维度 | 参数数量 |
| 卷积层(1×7@64) 批标准化 | [64, 1, 7] [64] | 448 |
| 卷积层2~11(1×3@64) 批标准化2~11 | [64, 64, 3] [64] | 12 288 |
| 卷积层2~12(1×3@64) 批标准化2~12 | [64, 64, 3] [64] | 12 288 |
| 卷积层2~21(1×3@128) 批标准化2~21 | [128, 64, 3] [128] | 24 576 |
| 卷积层2~22(1×3@128) 批标准化2~22 | [128, 128, 3] [128] | 49 152 |
| 卷积层2~31(1×3@256) 批标准化2~31 | [256, 128, 3] [256] | 98 304 |
| 卷积层2~32(1×3@256) 批标准化2~32 平均池化 | [256, 256, 3] [256] [256, 128, 1] | 196 608 32 768 |
| 全连接层 | [6, 195 072] | 1.17e+06 |
1.2 建立训练数据集
在搭建完网络模型后, 还需要建立完备的数据集以实现网络训练。利用飞行模拟器可以获得各战术机动动作的飞行数据, 每条飞行数据包含位置、速度、加速度、姿态角、姿态角速度等飞行参数。为降低网络计算量, 本文选取速度和加速度矢量作为飞行过程的特征参数。
为了避免网络在训练过程中出现过拟合, 提升数据集的完备性, 需要对已有的数据进行数据增强处理。常用的数据增强方法有翻转、旋转、平移等, 考虑到战术机动在改变航向时不能影响机动时的飞行特性, 所以本文中的飞行轨迹具有旋转不变特性。将轨迹绕Y轴旋转360°, 旋转间隔角度为1°, 设旋转角度为θ, 可得旋转矩阵为
坐标的变换过程如下:
式中: xa, ya, za为原始速度或加速度在北天东坐标系下的分矢量; RY为坐标旋转矩阵; xa′, ya′, za′为经过旋转变换后的速度或加速度分矢量。利用飞行模拟器虽然可以准确地获取飞行参数序列, 但是得到的点迹间隔很短, 通常为0.1 s左右, 这就导致了每条轨迹所包含的点迹数量十分庞大。为了降低网络计算量, 本文对每条轨迹进行采样处理, 将轨迹等间隔划分为100个区间, 在每个区间中随机采样, 这样每条轨迹可以获得100个点的采样数据并组成输入特征。其中, 每个点包含速度和加速度在北天东坐标系下的分矢量。为了让机器能够读懂每条数据所代表的意义, 数据集中每条数据不仅要有输入特征, 还要有对应的标签, 标签设置如表 2所示。
由表 2可以看出, 该问题是个多分类问题, 使用6种战术机动轨迹各7 200条(共43 200条)数据构成数据集。数据集在网络中会划分为训练集和测试集, 训练集用来更新网络权重, 测试集用来验证训练效果以及是否出现过拟合。当训练集和测试集的损失均较小时, 网络的分类和泛化能力较强; 当测试集损失远大于训练集损失时, 网络则可能出现过拟合现象, 代表网络过于信赖训练数据, 泛化能力较差。
将训练数据集输入到网络模型中, 根据数据中的特征信息, 网络模型可以利用梯度下降法, 通过BP算法不断地更新网络中权值的大小, 使得误差最小化, 并进行网络训练, 最终输出战术机动识别结果。
2 基于识别结果的飞行训练评估
2.1 评估指标
战术机动动作识别完成之后, 还需要对该机动飞行过程进行质量评估, 因此要构建合理的评估指标体系。由于每种战术机动动作的飞行特性既有相同之处, 也有不同之处, 不同类型战术机动动作的有效评估指标有所区别。构建的评估指标体系要能充分地体现机动飞行过程中的特征变化, 反映飞行品质, 指标评估标准要尽量合理、科学、简单并且实用。本文根据飞行员飞行大纲训练要求和相关领域专家经验, 构建的各种战术机动动作飞行训练评估指标如表 3所示。
表3 战术机动动作评估指标
Table 3
| 机动动作 | 标签 |
| 斤斗 | 进入速度, 载荷大小, 顶点速度 |
| 斜斤斗 | 进入速度, 顶点速度, 顶点坡度, 载荷大小 |
| 半滚倒转 | 进入速度, 改出速度 |
| 半斤斗翻转 | 进入速度, 顶点速度 |
| 半滚倒转-斤斗 | 同半滚倒转和斤斗指标 |
| 半滚倒转-半斤斗翻转 | 同半滚倒转和半斤斗翻转指标 |
表4 战术机动指标评估标准
Table 4
| 机动动作 | 评估指标标准 | 优秀 | 良好 | 合格 | 不合格 |
| 斤斗 | 进入速度(840 km/h) | ±40 | ±80 | ±120 | ±160 |
| 载荷大小(4.5 g) | ±0.2 | ±0.4 | ±0.6 | ±0.8 | |
| 顶点速度(300 km/h) | >390 | +60 | +30 | < 300 | |
| 斜斤斗 | 顶点坡度(35°) | ±3 | ±5 | ±7 | ±10 |
| 进入速度(840 km/h) | ±40 | ±80 | ±120 | ±160 | |
| 载荷大小(4.5 g) | ±0.2 | ±0.4 | ±0.6 | ±0.8 | |
| 顶点速度(300 km/h) | >390 | +60 | +30 | < 300 | |
| 半滚倒转 | 进入速度(500 km/h) | ±20 | ±40 | ±60 | ±80 |
| 改出速度(850 km/h) | ±40 | ±80 | ±120 | ±160 | |
| 半斤斗翻转 | 进入速度(800 km/h) | ±40 | ±80 | ±120 | ±160 |
| 顶点速度(350 km/h) | >440 | +60 | +30 | < 350 | |
| 半滚倒转-斤斗 | 该组合动作中半滚倒转阶段与半滚倒转机动动作评估标准一致, 斤斗阶段与斤斗机动动作评估标准一致 | ||||
| 半滚倒转-半斤斗翻转 | 该组合动作中半滚倒转阶段与半滚倒转机动动作评估标准一致, 半斤斗翻转阶段与半斤斗翻转机动动作评估标准一致 | ||||
2.2 评估方法
2.2.1 确定主观权重
表5 判断矩阵标度含义
Table 5
| 标度 | 含义 |
| 1 | 两个因素相比, 同样重要 |
| 3 | 一个因素比另一个因素稍显重要 |
| 5 | 一个因素比另一个因素明显重要 |
| 7 | 一个因素比另一个因素强烈重要 |
| 9 | 一个因素比另一个因素极端重要 |
| 2, 4, 6, 8 | 上述两相邻判断的中值 |
| 上列标度的倒数 | B与A相比是A与B相比的倒数 |
层次内单排序就是计算权重系数, 本文使用和积法(算术平均法)进行层次内单排序。
将判断矩阵的每一列元素归一化处理:
然后, 按行相加, 再按列归一化处理。
式中: i, j分别为行和列; n为指标数量。最终, 可求得判断矩阵的层次内单排序结果(即权重系数)。
由于判断矩阵是人为赋予的, 可能会出现指标间互相矛盾的现象, 所以要进行一致性检验。计算一致性指标(consistency index, CI):
查找平均随机一致性指标(random consistency index, RI), 如表 6所示, 并计算一致性比例(consistency ratio, CR)。
如果CR < 0.1, 则认为判断矩阵可以接受。
2.2.2 确定客观权重
Critic方法是一种通过评估指标的对比强度和冲突性来衡量指标的客观权值赋权法[27]。其中, 对比强度用标准差表示, 冲突性用相关系数表示, 计算过程如下。
(1) 设有m个样本, n个评估指标, 构建原始数据矩阵 X为
(2) 正向化处理:
(3) 计算指标的信息量:
式中: Sj代表了指标的数值差异性, Sj越大, 则信息量越多; Aj代表了指标之间的冲突性, Aj越大, 则各个指标之间的内容越没有重复; rij为指标i和指标j之间的皮尔逊相关系数。
计算得到信息量Cj为
信息量越大, 说明指标在整个指标评估体系中的作用越大, 权值也就越大。
(4) 计算客观权重:
计算得到的Wj即为指标j的客观权重大小。
2.2.3 确定组合权重
在获得主观权重和客观权重后, 博弈论方法可以在不同方法获得的权重之间找到一致或折中, 使得可能的权值与单个基值之间的偏差最小[28]。在博弈论组合赋权方法中, 首先构建权值向量 qk=[qk1, qk2, ⋯, qkn]。权值向量的任意线性组合可表示为
式中: σk为组合系数, l为赋权方法数量。为使得 q与 qk的离差最小化, 即
式(13)的最优化一阶导数为
计算得到(σ1, σ2, ⋯, σl), 进行归一化处理, 即可得到组合权重。
在确定完指标权重后, 需要对飞行过程中的每个指标进行量化评估, 具体评估规则如下:
式中: Ds为标准值; Di为实际值; Dmax为最大允许距离; S为评估结果。将评估结果划分为5个等级: 优秀(90~100), 良好(80~90), 中等(70~80), 合格(60~70), 不合格(< 60)。
3 仿真实验
仿真实验在计算机上运行, 运行环境为AMD Ryzen 7 5800H with Radeon Graphics 3.20 GHz处理器, 16 GB内存, Win11 64位操作系统, Python3.9.0。
3.1 分类器训练与测试
网络模型包含训练部分和验证部分, 在数据集中选取其中的80%作为训练集, 选取20%作为验证集, 并作为网络的输入。在网络开始训练之前, 需要使用一些方法来加快收敛速度, 避免参数过拟合。Mini-batch[29]是一种小批次训练方法, 可以避免大数据集导致的计算复杂的问题, 同时由一个batch中的数据决定梯度方向, 减少了梯度计算过程中的随机性。在本文实验中, batch大小选取为32。
为了避免因学习率设置不准确而导致网络收敛缓慢, 在网络中采用AdamW(Adam with weight decay, AdamW)优化算法[30], 该算法可以自适应调整学习率, 并且在参数更新时引入参数本身以避免过拟合问题。损失函数选择均方损失函数:
该损失函数处处可导, 确保梯度值可随学习率而变化, 可以很好地配合AdamW优化算法, 加快网络收敛, 计算方式如式(17)所示。在网络的全连接层后加入DropOut[31], 通过丢弃一部分参数使得网络不会过度依赖某些局部特征, 防止过拟合, 并增强网络模型的泛化能力。
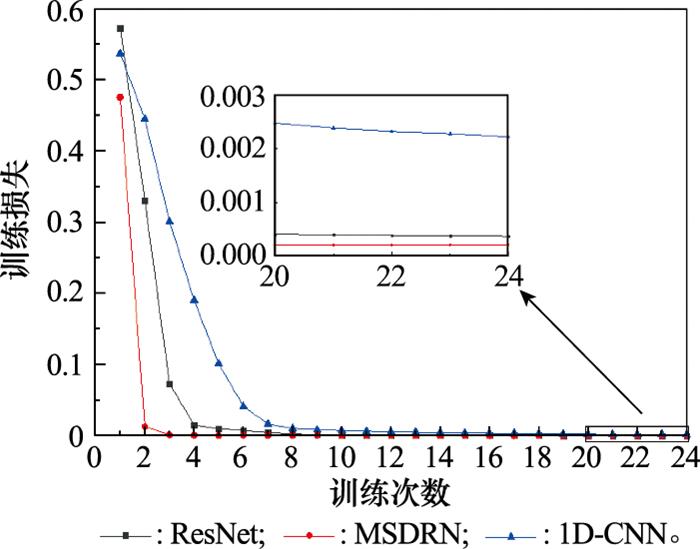
图4
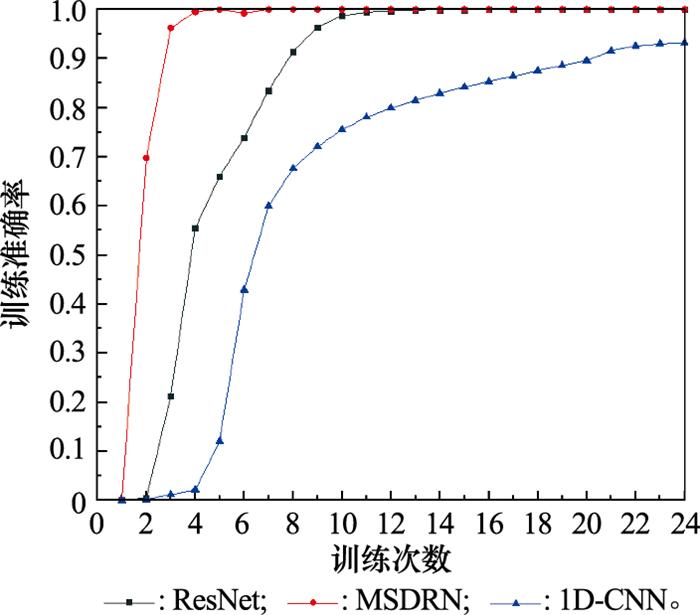
图5
测试另外选取两组飞行数据, 数据处理方式同训练数据集方式一样, 共生成4 320个测试样本, 将测试样本输入到网络中, 测试性能对比结果如表 7所示。
表7 测试性能对比
Table 7
| 网络模型 | 准确率/% | 运行时间/ms |
| 1D-CNN | 83.88 | 1.12 |
| ResNet | 96.50 | 15.90 |
| MSDRN | 100.00 | 12.10 |
由表 7可以看出, 1D-CNN虽然运行速度最快, 但是识别误差较大, 准确率最低, 只有83%左右, 原因是简单的网络结构虽然参数较少, 但是在样本数量不够充分的情况下表现不佳。ResNet准确度虽然高于1D-CNN, 但是运行时间最长, 原因是通过加深网络层数在提升识别准确率的同时加大了网络的计算量。上述两个网络结构测试结果与训练结果相比差别较大, 存在着一定的过拟合问题。MSDRN的测试结果与训练结果保持一致, 都达到了100%, 并且计算量低于ResNet, 在实现高准确度的同时保持着较高的运算效率, 相对而言表现最好, 表明了网络的横向拓展在一定程度上比纵向加深拓展的效果更好。
3.2 飞行训练质量评估
为了验证评估方法的有效性, 选取三组斤斗机动数据进行仿真实验, 首先根据速度和加速度进行机动类型识别, 识别结果如表 8所示。
表9 斤斗机动判断矩阵
Table 9
| 斤斗 | 进入速度 | 载荷大小 | 顶点速度 |
| 进入速度 | 1 | 2 | 1/2 |
| 载荷大小 | 1/2 | 1 | 1/3 |
| 顶点速度 | 2 | 3 | 1 |
由式(4)~式(7)计算可得一致性比例CR为
由于CR < 0.1, 认为该判断矩阵的一致性可以接受。由式(3)和式(4)可以计算得到层次分析法对应的飞行参数的指标权重大小为P1={0.3, 0.16, 0.54}。由式(7)~式(11)可以计算得到基于Critic方法的不同指标的权重大小为P2={0.33, 0.25, 0.42}。将P1和P2代入到式(13) 和式(14)中, 得到线性组合系数σ1*=0.34, σ2*=0.66。再由式(15)计算得到组合权重为P={0.32, 0.22, 0.46}, 分别代表了进入速度、载荷大小和顶点速度在评估过程中所占的比重。
然后, 对机动飞行过程的不同阶段进行分析以获取各个指标的实际飞机参数。为方便评估, 选取飞行过程中的进入段和顶点位置。在北天东坐标系下, 当速度的Y轴分量大于30 km/h或加速度值大于15 m/s2时, 视为机动开始; 当速度的Y轴分量发生正负变化时, 视为斤斗机动达到高度顶点, 载荷大小为从机动开始到高度顶点这一过程的平均载荷大小。
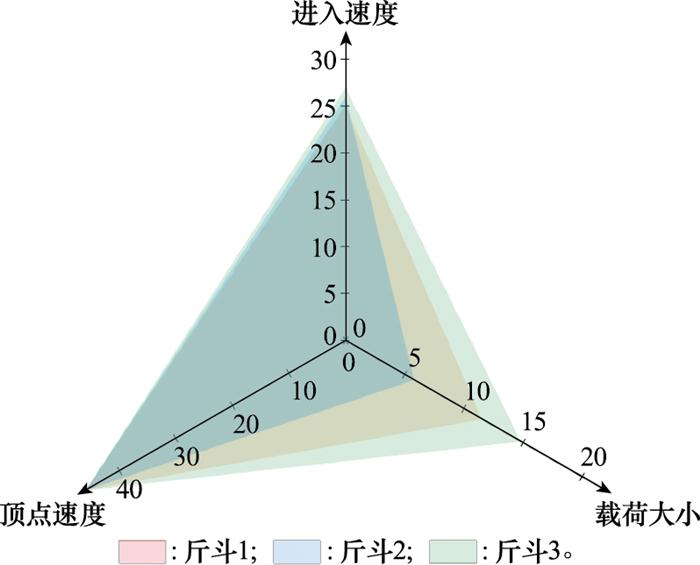
3条飞行轨迹在机动时的进入速度、载荷大小、顶点速度的实际值和偏差值如表 10所示。
表10 机动飞行参数
Table 10
| 机动类型 | 进入速度/(km/h) | 载荷大小/g | 顶点速度/(km/h) | |
| 斤斗1 | 实际值 | 874.47 | 4.88 | 551.24 |
| 偏差值 | +74.47 | +0.38 | +251.24 | |
| 斤斗2 | 实际值 | 870.08 | 5.09 | 587.47 |
| 偏差值 | +70.08 | +0.59 | +289.47 | |
| 斤斗3 | 实际值 | 864.60 | 4.76 | 541.31 |
| 偏差值 | +64.60 | +0.26 | +241.31 | |
表11 机动评估结果
Table 11
| 机动类型 | 进入速度 | 载荷大小 | 顶点速度 | 结果 |
| 斤斗1 | 78.46 | 52.50 | 100.00 | 82.66(良好) |
| 斤斗2 | 81.20 | 26.25 | 100.00 | 77.76(中等) |
| 斤斗3 | 84.63 | 67.50 | 100.00 | 87.93(良好) |
图6
在本文方法中, 首先对机动动作进行识别, 针对不同种类的机动动作有着不同的评估指标及评估标准, 提升了评估过程的可靠性。通过组合赋权方法得到的评估指标占比权重可以有效地区分出不同指标对于机动动作的重要程度, 可以根据此标准对飞行员进行针对训练, 以提升飞行质量。从评估结果可以看出, 基于机动动作识别的飞行训练质量评估方法是可行的, 可以对不同战术机动动作进行有效评估。
传统教练员打分均是基于部分观测数据的主观判断, 无法准确把握不同战术机动的评估指标节点, 并且对于不同指标的重要程度无法做出定量分析。本文提出的自动化的评估方法充分考虑到不同战术机动的飞行特性, 对每个评估指标做出定量分析, 评估方法科学合理, 更具说服性。
4 结束语
针对现有飞行训练质量评估方法的不足, 本文提出了一种基于战术机动识别和组合赋权的评估方法。其主要意义有以下几点: ①将战术机动识别归结为一个多分类问题, 使用基于多尺度特征的深度残差网络的战术机动识别方法, 对基本动作和组合动作均有较高的识别率, 对文中的6种机动动作类型的识别率达到了100%, 而且参数选择简单, 有很好的泛化性能, 为后续的飞行质量评估奠定了基础; ②结合战术机动飞行特性, 利用指标赋权方法, 完成了对不同战术机动动作种类的自动具体评估, 摆脱了对教练员的依赖, 评估结果同时融合了主观专家知识和客观数据特征, 使得评估结果更加科学合理。所提出的飞行训练质量自动评估方法降低了飞行训练成本, 提升了评估效率, 具有较好的应用价值。但是, 本文所提出的飞行质量自动评估方法只选取了部分飞行特征点, 未充分考虑战术机动动作的整体变化。在今后的研究中, 将飞行整体过程纳入评估指标考虑范围, 可以进一步提升评估效果。
参考文献
基于模糊支持向量机的飞机飞行动作识别
[J].
Fuzzy support vector machines based recognition for aeroplane flight action
[J].
基于运动分解和H-SVM的空战目标机动识别
[J].DOI:10.13195/j.kzyjc.2018.1210 [本文引用: 2]
Target maneuver recognition in air combat based on motion decomposition and H-SVM
[J].DOI:10.13195/j.kzyjc.2018.1210 [本文引用: 2]
Online hierarchical re-cognitionn method for target tactical intention in beyond-visual-range air combat
[J].DOI:10.1016/j.dt.2022.02.001 [本文引用: 1]
A flight maneuver re-cognition method based on multi-strategy affine canonical time warping
[J].DOI:10.1016/j.asoc.2020.106527 [本文引用: 2]
飞行成绩评定及管理系统
[J].DOI:10.3969/j.issn.1009-3516.2001.01.020 [本文引用: 2]
A kind of applied system for assessing and managing flying score
[J].DOI:10.3969/j.issn.1009-3516.2001.01.020 [本文引用: 2]
基于BP神经网络的飞行绩效评价模型
[J].DOI:10.13700/j.bh.1001-5965.2010.04.010 [本文引用: 2]
Pilot performance evaluation model based on BP neural networks
[J].DOI:10.13700/j.bh.1001-5965.2010.04.010 [本文引用: 2]
基于BP神经网络的飞行训练品质评估
[J].
Quality assessment of flight training based on BP neural network
[J].
基于动态贝叶斯网络和模糊灰度理论的飞行训练评估
[J].
Flight training evalu-ation based on dynamic Bayesian networkand fuzzy gray theory
[J].
基于MDTW的飞行动作识别算法
[J].
Flight action recognition algorithm based on MDTW
[J].
Evolving multi-label fuzzy classifier
[J].
Low-rank supervised and semi-supervised multi-metric learning for classification
[J].
Gradient-based learning applied to document recognition
[J].
A hybrid attention improved ResNet-based fault diagnosis method of wind turbines gearbox
[J].
Wider or deeper: revisiting the ResNet model for visual recognition
[J].
A comprehensive evaluation model for full-chain CCUS performance based on the analytic hierarchy process method
[J].
Optimization of evaluation indicators for driver's traffic literacy: an improved principal component ana-lysis method
[J].
层次分析法的研究与应用
[J].
Study and applications of analytic hierarchy process
[J].
Determining objective weights in multiple criteria problems: the critic method
[J].
Risk assessment of hybrid rain harvesting system and other small drinking water supply systems by game theory and fuzzy logic modeling
[J].
Dropout: a simple way to prevent neural networks from overfitting
[J].