系统工程与电子技术, 2023, 45(11): 3690-3698 doi: 10.12305/j.issn.1001-506X.2023.11.38

可靠性

基于多惩罚因子优化VMD的滚动轴承故障特征提取方法

李波1,2, 胡哿郗1,2, 石剑钧1,2, 刘恒畅1,2, 洪涛1,2

1. 电子科技大学航空航天学院, 四川 成都 611731

2. 飞行器集群智能感知与协同控制四川省重点实验室, 四川 成都 611731

Fault feature extraction method of rolling bearing based on multiple penalty factors optimization VMD

LI Bo1,2, HU Gexi1,2, SHI Jianjun1,2, LIU Hengchang1,2, HONG Tao1,2

1. School of Aeronautics and Astronautics, University of Electronic Science and Technology of China, Chengdu 611731, China

2. Sichuan Key Laboratory of Intelligent Sensing and Cooperative Control for Aircraft Cluster, Chengdu 611731, China

通讯作者: 李波

收稿日期: 2023-05-9  

基金资助: 四川省科技厅科技计划.  2023YFG0050
四川省科技厅科技计划.  2023YFG0039

Received: 2023-05-9  

作者简介 About authors

李波(1975—),男,教授,博士,主要研究方向为装备故障预测/诊断与维护、生产调度与过程控制 。

胡哿郗(1999—),男,硕士研究生,主要研究方向为装备故障诊断、复杂装备可靠性建模 。

石剑钧(1996—),男,助理工程师,硕士,主要研究方向为装备故障诊断与识别 。

刘恒畅(1997—),男,博士研究生,主要研究方向为装备维修决策与健康评估 。

洪涛(1977—),男,副研究员,博士,主要研究方向为航空宇航智能制造工程、装备故障诊断 。

摘要

针对变分模态分解(variational mode decomposition, VMD)在提取滚动轴承故障特征时预先设置多惩罚因子具有不确定性的问题, 结合灰狼优化(grey wolf optimization, GWO)算法提出一种基于多惩罚因子优化VMD的滚动轴承故障特征提取方法。首先利用GWO算法实现VMD的多惩罚因子自适应优化, 再利用优化得到的参数将滚动轴承的振动信号分解为多个本征模态函数(intrinsic mode function, IMF), 最后对各个IMF分量作包络解调提取滚动轴承的故障频率特征。研究结果表明, 在优化VMD参数时, 该方法相对其他方法优化效率有了明显提高, 并且提取滚动轴承故障特征效果显著, 得到特征频率幅值为其他方法的2~4倍, 证明了该方法的有效性和优越性。

关键词： 特征提取 ; 变分模态分解 ; 本征模态函数 ; 滚动轴承

Abstract

To solve the problem of uncertainty in pre-setting the penalty factor when the variational mode decomposition (VMD) is used to extract rolling bearing fault features, a rolling bearing fault feature extraction method is propose based on VMD optimization with multiple penalty factors using the grey wolf optimization (GWO) algorithm. Firstly, the GWO algorithm is used to achieve adaptive optimization of VMD with multiple penalty factors. Then, the vibration signal of the rolling bearing is decomposed into multiple intrinsic mode functions (IMF) using the optimized parameters. Finally, the fault frequency features of the rolling bearing are extracted by envelope demodulation of each IMF component. The results show that the optimization efficiency of the proposed method is significantly improved compared with other methods when optimizing VMD parameters, and the effect of extracting rolling bearing fault features is significant. The feature frequency amplitude obtained is 2 to 4 times higher than that of other methods, proving the effectiveness and superiority of the proposed method.

Keywords： feature extraction ; variational mode decomposition (VMD) ; intrinsic mode function (IMF) ; rolling bearing

PDF (4175KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李波, 胡哿郗, 石剑钧, 刘恒畅, 洪涛. 基于多惩罚因子优化VMD的滚动轴承故障特征提取方法. 系统工程与电子技术[J], 2023, 45(11): 3690-3698 doi:10.12305/j.issn.1001-506X.2023.11.38

LI Bo. Fault feature extraction method of rolling bearing based on multiple penalty factors optimization VMD. Systems Engineering and Electronics[J], 2023, 45(11): 3690-3698 doi:10.12305/j.issn.1001-506X.2023.11.38

0 引言

滚动轴承因其摩擦阻力小、功率消耗小和机械效率高等特点, 被广泛应用于航空发动机[1-2]、铁路运输设备[3-4]以及大型工业机械设备[5-6], 承担动力传递和动力转换的任务, 是机械发生故障的主要故障源之一[7-8]。由于滚动轴承的健康状态直接关系设备的安全稳定运行, 因此及时发现关键滚动轴承中存在的故障, 对确保机械安全稳定运行具有重大意义[9]。通常情况下, 机械设备运行状态的变化可通过其动态信号(例如振动信号)进行有效反映, 利用信号处理技术分离出其中隐藏的故障特征信息。然而, 其动态信号中蕴含了复杂机械结构中各个部件产生的信号成分, 而且不可避免地存在背景噪声, 导致其中的故障特征信息被干扰成分淹没。同时, 滚动轴承复杂的工况使得动态信号表现出调频、调幅等复杂的时变特性, 提高了提取其故障特征信息的难度[10-11]。由于上述轴承工作环境的特点, 如何在复杂噪声环境下有效提取滚动轴承故障特征变得非常关键。

迄今为止, 学者们提出了多种信号处理技术提取滚动轴承振动信号中的故障特征信息, 而最有效的则是基于时频域的信号处理技术。研究初期, 小波变换被应用于滚动轴承的故障特征提取中, 实现了对信号时频变化特性的分析, 但其变换效果极其依赖经验选取的小波基函数[12]。为此, Huang等[13]首次提出了一种自适应时频处理的经验模态分解方法, 合理解决了小波变换存在的“基选择”经验依赖问题, 但其同时也存在端点效应和模态混叠的缺点。在此基础上, Wu等[14]提出了集成经验模态分解, 有效地解决了经验模态分解存在的模态混叠现象, 但该方法存在一个白噪声选择问题, 易出现分解效果不佳的情况。进而, Dragomiretskiy等[15]提出了变分模态分解方法, 相比于集成经验模态方法具有更好的信号局部性能和更优的噪声抑制能力, 但也存在分解过程中参数难以设定的缺点。

为了解决变分模态分解中参数难以确定的问题, 学者们陆续开展了相应研究。王奉涛等[16]提出通过分解信号的能量差值来确定分解层数。毕凤荣等[17]提出通过计算分解后各个本征模态函数(intrinsic mode function, IMF)的中心频率差值来确定分解层数。李华等[18]提出通过最大峭度原则优化分解层数。然而，上述研究只优化了变分模态分解(variational mode decomposition, VMD)分解层数和惩罚因子中的一个, 没有全面考虑到这两个参数之间的相互作用对分解效果的影响。为此, 程军圣等[19]以正交低峰值为优化目标函数, 利用萤火虫算法对分解层数与惩罚因子进行联合优化。唐贵基等[20]提出以信号包络熵作为粒子群算法的优化目标函数对参数进行优化。Xu等[21]引入Teager能量算子并结合最大峭度系数和平均峭度系数优化分解层数和惩罚因子。虽然上述研究实现了VMD分解层数与惩罚因子的自适应设定, 解决了需手动设置参数的问题, 但没有考虑IMF各个分量对应的惩罚因子αk对VMD结果的影响。因此, 郑圆等[22]利用智能算法确定了分解层数和多惩罚因子αk, 然而其在建立优化目标函数时, 只考虑了分解后信号与原始信号的时域差异, 无法有效地反映分解后信号包含原始信号的信息完整度。由此可见, 当前利用VMD提取滚动轴承的故障特征时, 其预先设置惩罚因子具有不确定性的问题并未得到合理解决, 仍存在较大提升空间。

因此, 本文提出一种基于多惩罚因子优化VMD的滚动轴承故障特征提取方法。首先, 构建了融合皮尔逊相关系数、时频谱相似度以及最大峭度值的优化目标, 然后, 通过最大峭度准则优化其分解层数, 再利用灰狼优化(grey wolf optimization, GWO)算法获取最佳分解层数以及最佳分解模态函数, 保证了分解后模态函数最大限度地包含原始信号的故障特征信息, 提升了滚动轴承振动信号经提取后故障特征的显著性。最后, 利用公开数据集分析验证, 通过对比多种不同方法, 得出本文所提方法的故障特征提取效果优于其他同类方法, 证明了该方法的有效性。

1 算法基本原理

1.1 VMD算法分解原理

VMD非递归式地将具有多个频率成分的实信号分解为多个本征模态函数uk, 并求得每个uk的单边谱, 同时对每个uk进行调频, 最后添加约束条件得到一个带约束的变分模型[23]:

$\begin{array}{c}\mathop {\min }\limits_{_{\left\{ {{u_k}} \right\}\left\{ {{\omega _k}} \right\}}} \left\{ {\sum\limits_{k = 1}^K {\left\| {\frac{{\partial \left[ {\left( {\delta (t) + \frac{{\rm{j}}}{{{\rm{ \mathsf{ π}}} t}}} \right) \cdot {u_k}(t)} \right]}}{{\partial t}} \cdot {{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}} \right\|_2^2} } \right\}\\{\rm{ s}}{\rm{.t }}\sum\limits_k^K {{u_k}} = f\end{array}$

式中: ωk是假设分解得到的各阶模态分量的频率中心; uk是第k个IMF模态分量; f是原始信号; δ(t)为一脉冲函数。

通过拉格朗日函数将上述问题转化为无约束变分问题[15]:

$\begin{array}{c} L_{\left(u_{k}, \omega_{k}, \lambda\right)}=\alpha \sum\limits_{k=1}^{K}\left\|\frac{\partial\left[\left(\delta(t)+\frac{\mathrm{j}}{{\rm{ \mathsf{ π}}} t}\right) \cdot u_{k}(t)\right]}{\partial t} \cdot \mathrm{e}^{-\mathrm{j} \omega_{k} t}\right\|_{2}^{2}+\\\left\|f(t)-\sum\limits_{k=1}^{K} u_{k}(t)\right\|_{2}^{2}\left\langle\lambda(t), f(t)-\sum\limits_{k=1}^{K} u_{k}(t)\right\rangle\end{array}$

式中: α为惩罚因子; λ为拉格朗日乘子。再利用交替乘子方向算法求解, 更新各IMF分量的中心频率以及带宽[15]:

$\omega_{k}^{n+1}=\frac{\int_{0}^{\infty} \omega\left|\hat{u}_{k}(\omega)\right|^{2} \mathrm{~d} \omega}{\int_{0}^{\infty}\left|\hat{u}_{k}(\omega)\right|^{2} \mathrm{~d} \omega} $

$\hat{u}_{k}^{n+1}(\omega)=\frac{\hat{f}(\omega)-\sum\nolimits_{i \neq k} \hat{u}_{i}(\omega)+(\hat{\lambda}(\omega) / 2)}{1+2 \alpha\left(\omega-\omega_{k}\right)^{2}}$

式中: $ \hat{u}_{k}^{n+1}(\omega)$是当前残余量$ \hat{f}(\omega)-\sum\nolimits_{i \neq k} \hat{u}_{i}(\omega)$的滤波结果; ωkn+1为第k个IMF的功率谱重心。通过傅里叶逆变换求得信号实部$ \hat{u}_{k}(t)$。

1.2 GWO算法原理

GWO算法将灰狼种群捕食活动中的追踪、接近、围捕以及进攻行为模拟运用到算法搜索寻优过程中, 其种群将个体分为4个等级: α、β、γ和ω。通过前3种最好的个体α、β、γ引导群体向猎物方向(即最优解)靠近, 该算法原理比较简单。相比其他算法, 在运算过程中需要调整的参数较少且比较容易实现, 且收敛速度较快, 收敛结果较准[23]。

灰狼种群追捕猎物的公式为

$\boldsymbol{D}=\left|\boldsymbol{C} \cdot \boldsymbol{X}_{p}(t)-\boldsymbol{X}(t)\right| $

$\boldsymbol{X}(t+1)=\boldsymbol{X}_{p}(t)-\boldsymbol{A} \cdot \boldsymbol{D}$

式中: C和A为系数; Xp(t)为猎物位置; X(t)为灰狼位置。C和A的更新公式为

$\boldsymbol{C}=2 \boldsymbol{r}_{2} $

$\boldsymbol{A}=2 \boldsymbol{a} \boldsymbol{r}_{1}-\boldsymbol{a}$

式中: r1和r2为随机系数, 其模值范围为[0, 1]; a为收敛因子, 随迭代次数从2到0线性递减。再由式(5)和式(6)求出3条头狼的位置Xα(t+1)、Xβ(t+1)、Xγ(t+1), 然后通过3条头狼的位置确定种群中其他灰狼的位置:

$X(t+1)=\frac{X_{\alpha}(t+1)+X_{\beta}(t+1)+X_{\gamma}(t+1)}{3}$

GWO算法根据当前解空间中前3个最优解搜索全局最优解, 同时在搜索过程充分借助辅助系数改变某个体权重, 因此算法陷入局部最优的概率较低。

2 基于GWO-VMD的滚动轴承故障特征提取方法

2.1 基于皮尔逊相关函数、最大峭度和时频谱相似度的优化目标函数

原始信号分解后的信号不能丢失原始信号的关键信息特征, 且分解后的信号应更明显地体现出其内部的特征, 否则做此分解操作并无意义。因此，量化分解效果的有效性应有两个准则[24-26]: 一是分解后的信号应尽量包含原始信号完整信息; 二是分解后应更明显地突出故障特征。

基于上述两个准则, 本研究提出3个优化目标: 皮尔逊相关系数、时频谱相似度以及最大峭度。

(1) 皮尔逊相关系数

皮尔逊相关系数可衡量两种信号的线性相关程度, 绝对值越大代表线性相关的程度越强。

首先将信号进行VMD, 然后通过得到的模态分量将信号重构, 得到重构信号X(t), Xi为重构信号X(t)某一个样本点。设原始信号为S(t), Si为原始信号S(t)某一个样本点, 则可计算X(t)和S(t)的皮尔逊相关系数如下:

$r=\frac{1}{N-1} \sum\nolimits_{i=1}^{N}\left(\frac{X_{i}-\bar{X}}{\sigma_{X}}\right)\left(\frac{S_{i}-\bar{S}}{\sigma_{S}}\right)$

式中: $ \frac{X_{i}-\bar{X}}{\sigma_{X}} $、$ \bar{X}$及σX分别是对Xi样本的标准分数、样本均值和样本标准差; N为信号采样长度。

(2) 时频谱相似度

时频谱能够描述两种信号在时域上其频率成分的变化情况, 恰好解决了非平稳信号在时域上其频率不断变化的问题, 通过时频谱相似度可以有效地反映两种非平稳信号的相关性。

利用希尔伯特黄变换求得重构信号时频谱Xt-f和原始信号时频谱St-f, 其时频谱相似度为

$S_{\mathrm{im}}=\frac{1}{N} \sum\limits_{i=1}^{N}\left|X_{t-f}(i)-S_{t-f}(i)\right|$

(3) 最大峭度

峭度是一种无量纲参数。通常情况下滚动轴承振动信号峭度值为3左右, 信号幅值呈正态分布, 当出现故障时, 振动信号峭度值增大且信号幅值偏离正态分布。峭度值越大, 表明该滚动轴承故障越严重。

当原始信号分解后, 其各个模态分量中的最大峭度越大, 说明分解后的信号故障特征变现越明显, 因此计算分解后各个本征模态分量的峭度, 取最大的峭度:

$\operatorname{Kur}_{\max }=\max \left(\frac{1}{N_{j}} \sum\limits_{i=1}^{N_{j}}\left(\frac{x_{i}-\bar{x}}{\sigma_{t}}\right)^{4}\right)$

式中: xi为信号值; ${\bar x}$为信号的均值; σt为标准差。

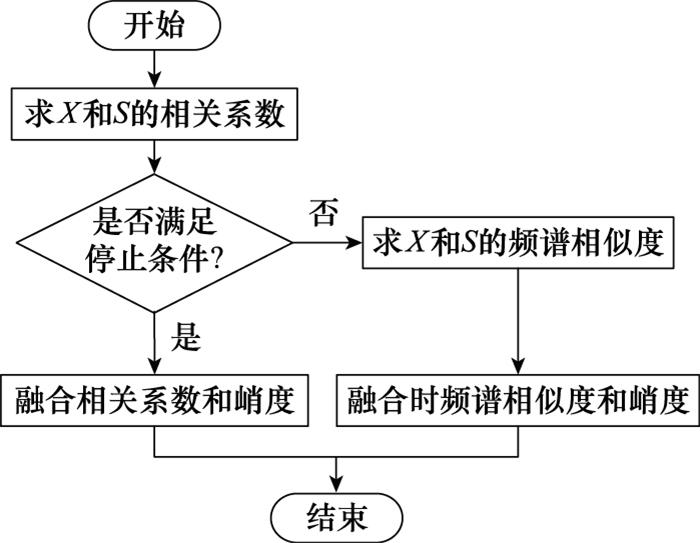
两个时域信号的皮尔逊相关系数只能表征两个信号时域上的相关性, 且在此背景下, 皮尔逊相关系数只有正向判定而无反向判定, 即数值高表征两个信号高度相似, 但数值低并不能表征两个信号毫无相关性。因此，求得以上3个指标后, 引入阈值融合皮尔逊相关系数、时频谱相似度和最大峭度, 融合流程图如图 1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   融合3个目标流程图

Fig.1   Flow chart of integrating three objective


如图 1所示, 当两种信号的皮尔逊相关系数大于某阈值时, 则可充分表明重构信号包含原始信号的完整信息特征, 因此融合最大峭度系数, 提高其对故障特征的敏感性, 不必再进行大量的计算求得时频谱相似度。当皮尔逊相关系数小于阈值, 此时皮尔逊相关系数失效, 必须求得时频谱相似度来标定重构信号与原始信号的相关性。

2.2 基于GWO-VMD的滚动轴承故障特征提取方法

在VMD算法中惩罚因子α是一个重要的参数, 其决定着VMD后各IMF的带宽。通常, 滚动轴承的振动信号包含谐波分量与脉冲分量, 谐波信号频带带宽较小, 因此VMD时需要较大的α, 有利于提取其特征; 而故障脉冲信号相反, 其时域较短, 频带带宽较大, 因此VMD时需要较小的α, 有利于提取其特征。

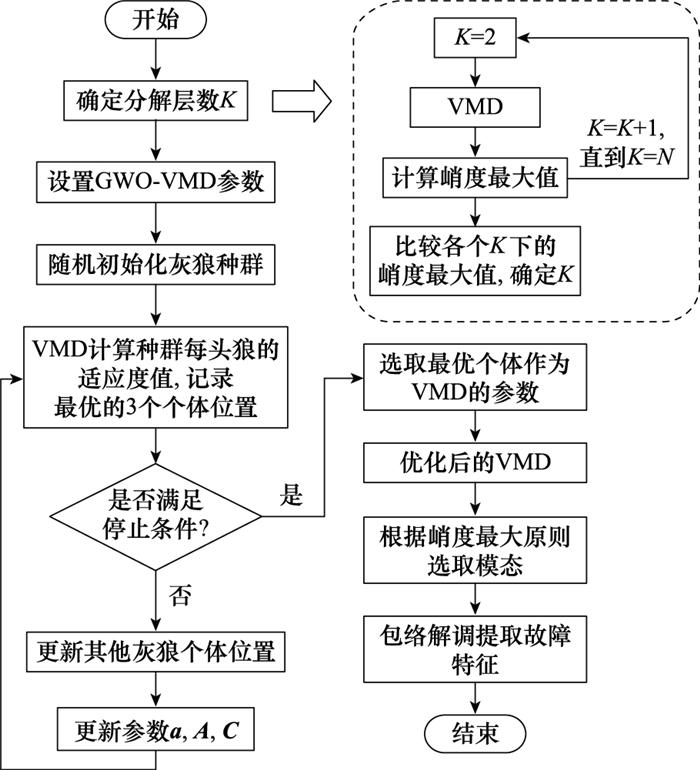
由此可见, 单惩罚因子VMD无法同时提取滚动轴承振动信号包含的谐波特征与故障脉冲特征。因此, 本文首先利用最大峭度准则优化VMD的分解层数K, 然后通过GWO算法, 以上文的优化目标函数为适应度, 为每个IMF分量搜寻最优的惩罚因子, 信号经分解后, 对各个本征模态分量作包络谱分析, 提取其故障频率特征。算法具体流程图如图 2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   GWO-VMD算法流程图

Fig.2   Flow chart of GWO-VMD algorithm


算法具体步骤如下所示。

步骤1  首先需要确定分解层数K的值, 设置K从2递增到n, 每次迭代中对振动信号作VMD得到K个模态分量, 分别求得每个本征模态分量的峭度值, 并取最大值, 取第一个达到极大值时对应的K。

步骤2  设置GWO初始参数a, A、C的值。

步骤3  以Xi=(Xi1, Xi2, …, XiK)作为第i个灰狼的位置, 范围取100到8 000, 随机初始化灰狼种群内N只灰狼个体的位置。

步骤4  将每只灰狼的位置Xi作为惩罚因子[α1, α2, …, αK]对信号进行VMD, 根据式(10)~式(12)计算得出适应度值, 并记录最优的3个头狼个体位置Xα、Xβ和Xγ。

步骤5  通过式(9)更新其他灰狼个体的位置, 并通过式(7)和式(8)更新参数A、C和a的值。

步骤6  循环执行步骤4和步骤5, 直至迭代完毕。

步骤7  选取适应度值最大的个体作为优化后的惩罚因子[α1, α2, …, αK]以及最佳分解层数K作为VMD参数对信号作分解。

步骤8  对各个IMF做包络解调, 提取故障特征信息。

3 实验与分析

3.1 数据源选择

本实验数据来源于某电气工程实验室的滚动轴承数据, 是相关研究学者普遍采用的数据集。该实验采用一个参数可调节的电机作为负载, 负载可为1 hp、2 hp以及3 hp。实验中的故障类型为表面加工的单点故障。实验中被测试的轴承有两种, 其中SKF型号轴承的故障直径包含0.007 mils、0.014 mils、0.021 mils, NTN型号轴承的故障直径包含0.028 mils以及0.040 mils。本研究选择了故障直径为0.021 mils的SKF型号轴承振动信号数据来验证所提方法的有效性, 其转速为1 772 r/min, 采样频率为12 kHz。

3.2 实验过程与结果分析

首先, 根据模型算法求得最佳分解层数, 固定分解因子, 计算出不同分解层数对应的最大峭度值, 最大峭度与分解层数的关系图如图 3所示。由图 3可以观察到，最大峭度值对应的分解层数为4, 因此最佳分解层数为4层。求出最佳分解层数后, 运用GWO-VMD算法, 为每层模态求得最佳的惩罚因子。

图3

新窗口打开| 下载原图ZIP| 生成PPT

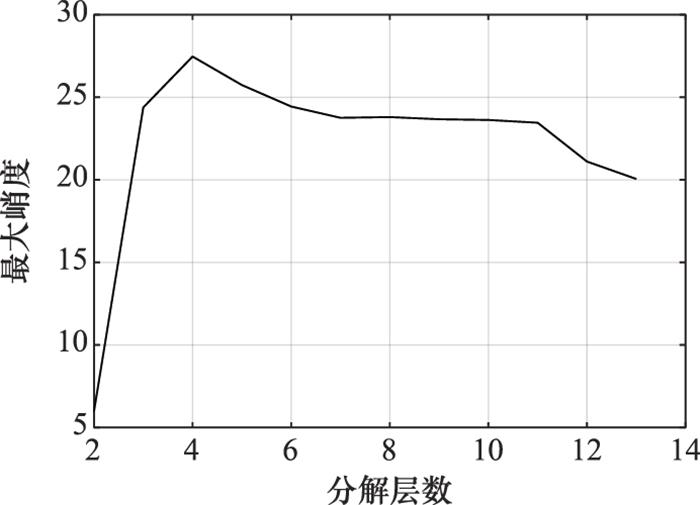
图3   最大峭度与分解层数的关系

Fig.3   Relationship between the maximum kurtosis and the number of decomposition layers


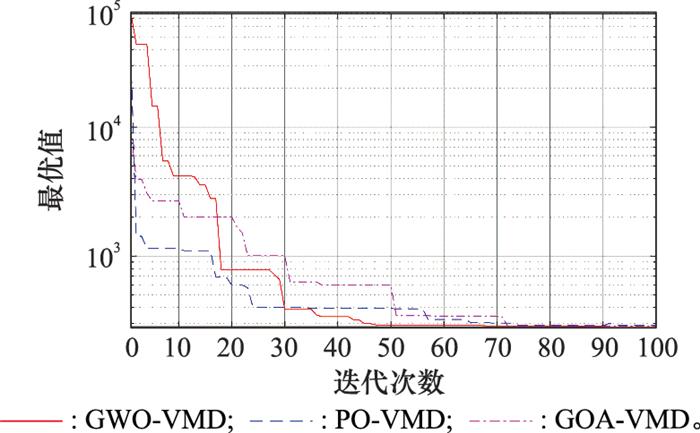
本实验还将本算法与基于参数优化的VMD(parameter optimized VMD, PO-VMD)、基于蝗虫优化算法的VMD(grasshopper optimization algorithm-VMD, GOA-VMD)两种算法求解最优值的收敛情况进行对比, 3种算法的收敛迭代折线图如图 4所示。从图 4中可观察到，GWO-VMD算法收敛效果最好, 在47代左右基本收敛达到最优值；PO -VMD算法虽在前期收敛较快, 但最终在70代左右才基本收敛达到最优值; GOA-VMD算法的效果则完全不如GWO -VMD算法。表 1为各算法达到最优值的收敛情况, 可观察到虽然PO-VMD算法可达到最快的收敛速度, 但其整体性能远远不如GWO-VMD算法, 而GOA-VMD算法各项指标都不如GWO-VMD算法, 因此可表明GWO-VMD算法的效率性强于其他算法。由算法求得4层对应的惩罚因子分别为[5 224, 4 110, 1 860, 540]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   3种算法的迭代收敛图

Fig.4   Iterative convergence plots of three algorithms


表1   3种算法收敛情况

Table 1  Convergence of three algorithms

算法迭代次数
最小值最大值平均值中位数
GWO-VMD415748.6248
PO-VMD398269.8271
GOA-VMD518772.1674

新窗口打开| 下载CSV


将上述求得的最佳分解层数和惩罚因子代入, 对信号作VMD, 并通过分解后的各个模态分量重构原始振动信号数据如图 5和图 6所示。由图 5和图 6可观察到, 原始信号与重构信号的时域波形及其相似。对这两种信号作包络解调, 如图 7所示, 可观察到原始信号与重构信号的包络谱图极其相似, 重构信号包络谱图仅仅在某些频率上的幅值有些许损失, 因此表明该重构信号包含原始信号的完整特征, 证明了该方法的有效性。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   原始振动信号波形图

Fig.5   Waveform diagram of original vibration signal


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   重构信号波形图

Fig.6   Waveform diagram of reconstructed signal


图7

新窗口打开| 下载原图ZIP| 生成PPT

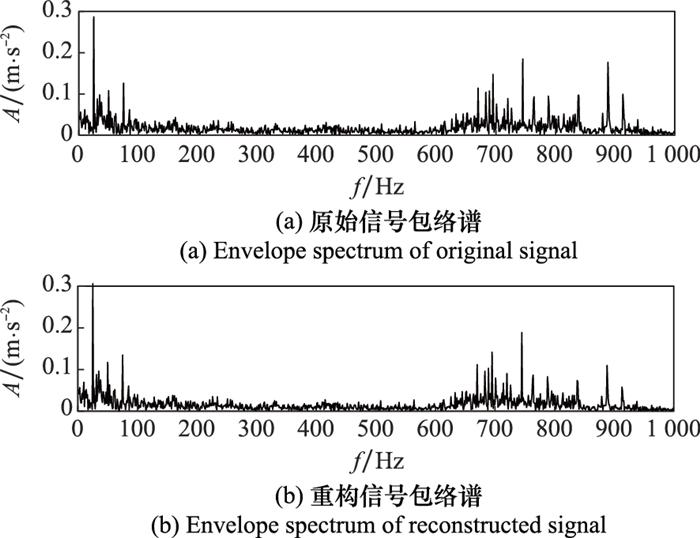
图7   原始信号与重构信号包络谱

Fig.7   Envelope spectrum of original signal and reconstructed signal


再进一步对信号作分解, 并求出各个IMF分量的频谱图。GWO-VMD算法分解后各个IMF的时域波形图以及对应的频谱图如图 8所示。可观察到，原始信号通过分解后, 分离出了各个频段部分的分量, 分解效果较好。PO -VMD算法和VMD算法分解各分量时域波形和频谱分别如图 9和图 10所示。可以观察到，图 9中IMF2的频谱图与IMF4频谱图处有重叠, 并且在低频处丢失了信号应有的频率特征。图 10也有相似的特点, 图 10中IMF1的频谱图与IMF4的频谱图处有重叠, 也丢失了信号本该有的低频特征, 这证明了本文方法的有效性以及优越性。

图8

新窗口打开| 下载原图ZIP| 生成PPT

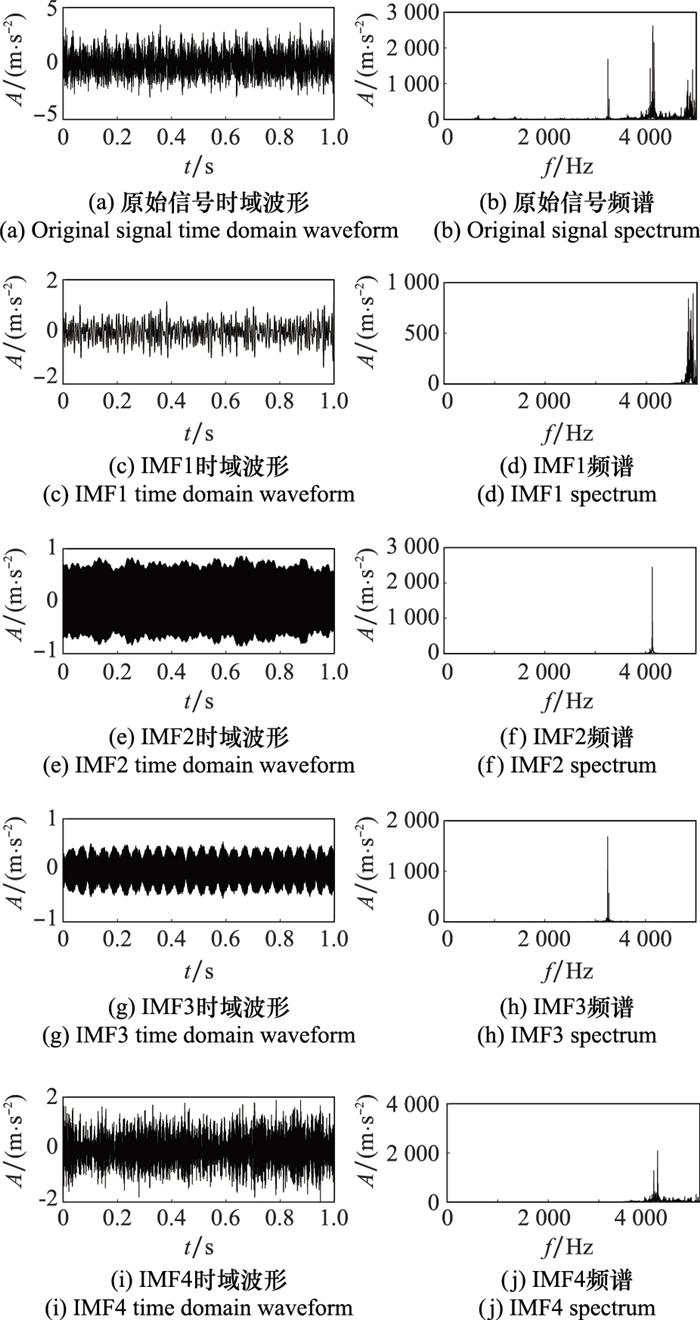
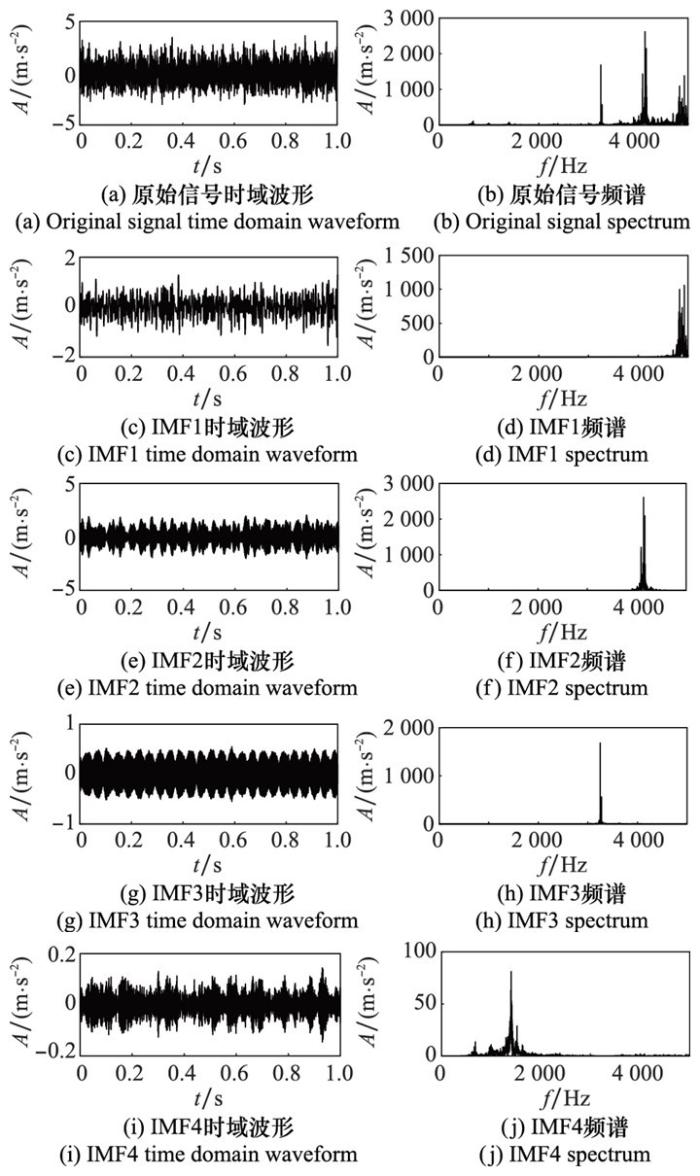
图8   GWO-VMD各分量时域波形和频谱

Fig.8   Time domain waveform and spectrum of each component by GWO-VMD


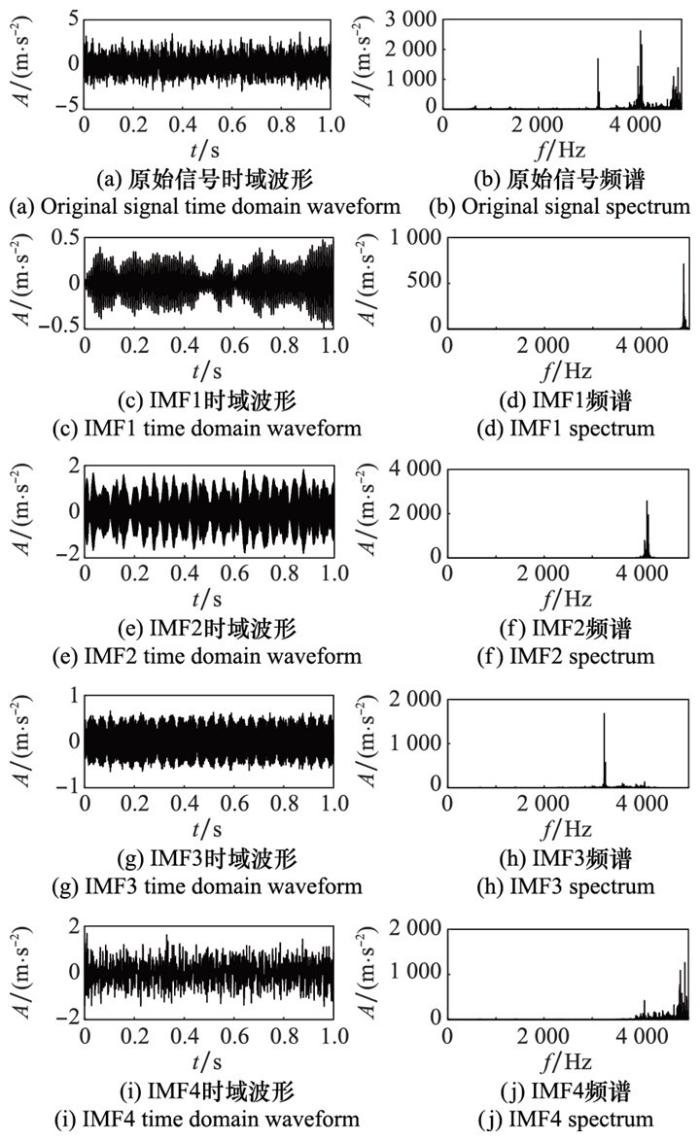
图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   PO-VMD各分量时域波形和频谱

Fig.9   Time domain waveform and spectrum of each component by PO-VMD


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   VMD各分量时域波形、频谱

Fig.10   Time domain waveform and spectrum of each component by VMD


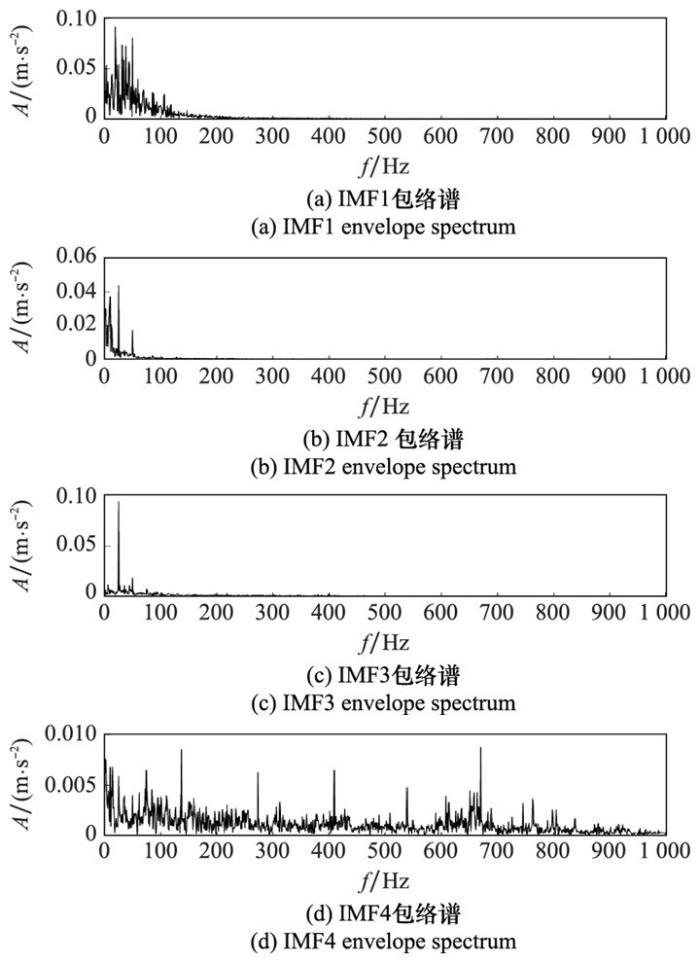
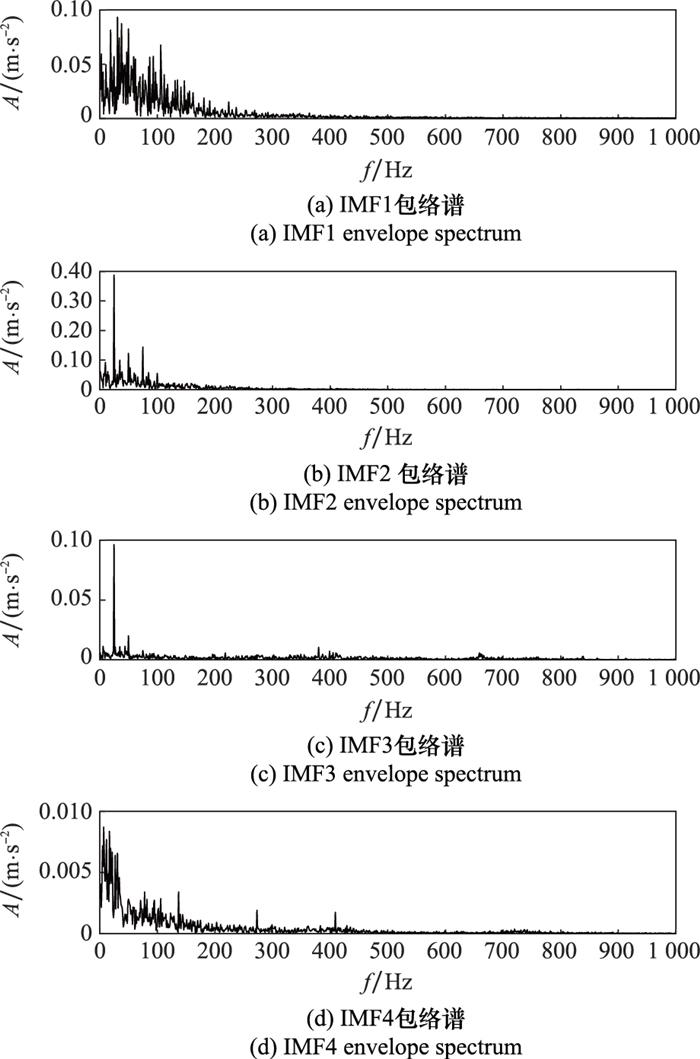
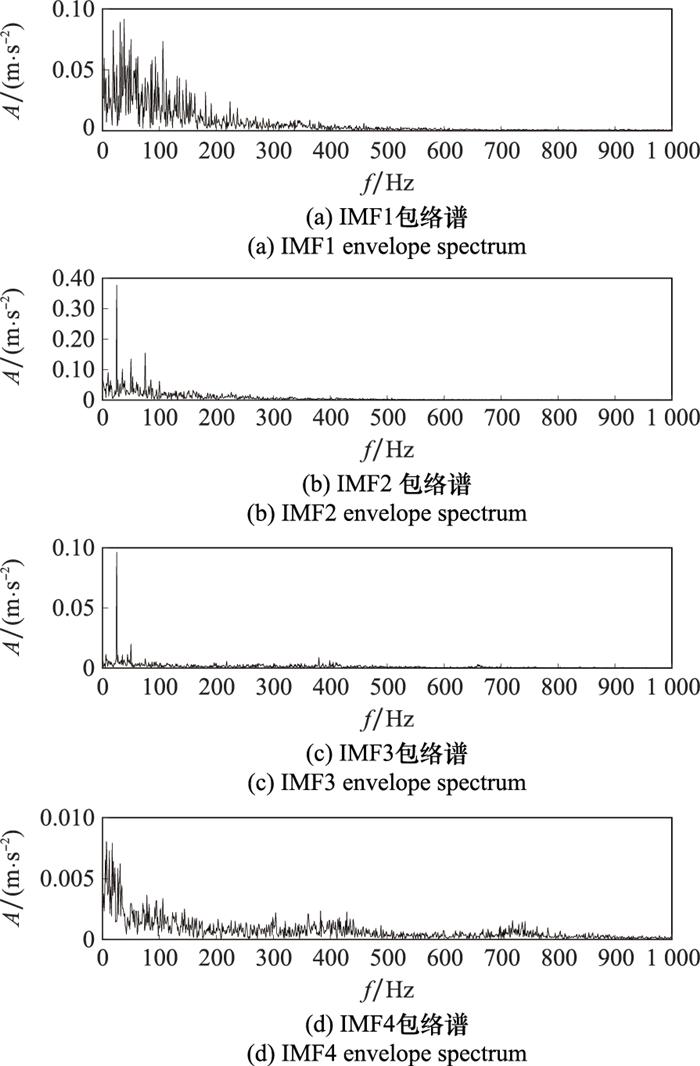
然后，再对3种算法分解得到的IMF分量作包络解调, 得到各个IMF分量的包络谱图。GWO-VMD后各IMF的包络图如图 11所示。可以看到，在故障频率处以及其2~5倍频处有明显的谱峰, 说明提取到了其故障特征频率, 证明本文提出方法的有效性, 并且谱图在故障频率及其倍频处比较干净, 干扰较少。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   GWO-VMD后4个IMF的包络谱

Fig.11   Envelope spectrum of four IMF after GWO-VMD


PO-VMD后的各IMF包络谱图如图 12所示。从图 12可以观察到, 通过PO -VMD后, 虽在IMF4包络谱图中在故障特征频率处以及其2~3倍频处有谱峰, 但是其谱峰不是很明显, 受周围噪声频率干扰会比较大, 并且在4倍频以及4倍频以上处基本看不到谱峰, 抑制效果过于严重导致所需要的故障特征也被抑制, 无法有效地表征信号中蕴含的故障特征信息。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   PO-VMD后各IMF的包络谱

Fig.12   Envelope spectrum of each IMF after PO-VMD


VMD后的各IMF包络谱图如图 13所示。从图 13可观察到, VMD后各个IMF都出现了较大的噪声, 分解过程中噪声抑制不明显, 并且分解后频率成分几乎集中在低频中, 该频段噪声干扰很大, 无法有效地观察到故障频率特征。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   VMD后各IMF的包络谱

Fig.13   Envelope spectrum of each IMF after VMD


上述分析结果表明了本文方法提取效果更好, 能够更有效地提取出故障特征频率。表 2中列出了3种方法提取的特征频率幅值情况, 并做了归一化方便对比。同时，从表 2也可以观察到本文所提的GWO-VMD方法提取的特征频率幅值远大于其他两种对比方法, 进一步验证了本方法的有效性和优越性。

表2   3种算法提取特征频率幅值

Table 2  Characteristic frequency and amplitude extracted by three algorithms

算法特征频率
fi2fi3fi4fi5fi
VMD0.2180.1760.1120.0710.104
PO-VMD0.4160.2730.2610.0180.012
GWO-VMD0.8570.6820.6910.4830.841

新窗口打开| 下载CSV


4 结论

本文提出了一种基于多惩罚因子优化VMD的滚动轴承故障特征提取方法, 该方法以VMD理论为基础, 以提升故障特征显著性和包含信息完整性为目标, 构建融合皮尔逊相关系数、时频谱相似度以及最大峭度值的优化目标函数, 并利用GWO算法自适应地搜索VMD的最佳分解层数和每个IMF分量对应的惩罚因子, 解决了VMD需根据经验手动设置参数导致分解效果不佳的问题, 实现了滚动轴承故障特征的有效提取。实验结果分析表明, GWO-VMD与PO -VMD和VMD等算法相比, 可以在噪声环境下有效地提取轴承故障特征。

参考文献

康玉祥, 陈果, 尉询楷, 等.

基于残差网络的航空发动机滚动轴承故障多任务诊断方法

[J]. 振动与冲击, 2022, 41 (16): 285- 293.

DOI:10.13465/j.cnki.jvs.2022.16.037      [本文引用: 1]

KANG Y X , CHEN G , YU X K , et al.

A multi-task fault diagnosis method of rolling bearings based on the residual network

[J]. Journal of Vibration and Shock, 2022, 41 (16): 285- 293.

DOI:10.13465/j.cnki.jvs.2022.16.037      [本文引用: 1]

李泽东, 李志农, 陶俊勇, 等.

基于特征融合的注意力增强卷积神经网络的航空发动机滚动轴承故障诊断方法

[J]. 兵工学报, 2022, 43 (12): 3228- 3239.

URL     [本文引用: 1]

LI Z D , LI Z N , TAO J Y , et al.

Fault diagnosis for aero-engine rolling bearings based on an attention augmented convolutional neural network with feature fusion

[J]. Acta Armamentarii, 2023, 43 (12): 3228.

URL     [本文引用: 1]

杨志军. 基于优化MOMEDA与改进PSO-Elman的铁路列车滚动轴承故障诊断研究[D]. 北京: 北京交通大学, 2022.

[本文引用: 1]

YANG Z J. Research on fault diagnosis of rolling bearings of railway trains based on optimized MOMEDA and improved PSO-Elman[D]. Beijing: Beijing Jiaotong University, 2022.

[本文引用: 1]

YAN G X , CHEN J , BAI Y , et al.

A survey on fault diagnosis approaches for rolling bearings of railway vehicles

[J]. Processes, 2022, 10 (4): 724.

DOI:10.3390/pr10040724      [本文引用: 1]

柳晓龙. 基于深度学习的滚动轴承故障诊断系统的设计与实现[D]. 沈阳: 中国科学院沈阳计算技术研究所, 2022.

[本文引用: 1]

LIU X L. Design and implementation of rolling bearing fault diagnosis system based on deep learning[D]. Shenyang: Shenyang Institute of Computing Technology, Chinese Academy of Sciences, 2022.

[本文引用: 1]

HU J , DENG S E .

Rolling bearing fault diagnosis based on wireless sensor network data fusion

[J]. Computer Communications, 2022, 181, 404- 411.

DOI:10.1016/j.comcom.2021.10.035      [本文引用: 1]

陈是扦, 彭志科, 周鹏.

信号分解及其在机械故障诊断中的应用研究综述

[J]. 机械工程学报, 2020, 56 (17): 91- 107.

URL     [本文引用: 1]

CHEN S Q , PENG Z K , ZHOU P .

Review of signal decomposition theory and its applications in machine fault diagnosis

[J]. Journal of Mechanical Engineering, 2020, 56 (17): 91- 107.

URL     [本文引用: 1]

WU G G , YAN T Y , YANG G L , et al.

A review on rolling bearing fault signal detection methods based on different sensors

[J]. Sensors, 2022, 22 (21): 8330.

DOI:10.3390/s22218330      [本文引用: 1]

DENG W , LI Z X , LI X Y , et al.

Compound fault diagnosis using optimized MCKD and sparse representation for rolling bearings

[J]. IEEE Trans.on Instrumentation and Measurement,, 2022, 71, 3508509.

[本文引用: 1]

WANG Z L , YANG J H , GUO Y .

Unknown fault feature extraction of rolling bearings under variable speed conditions based on statistical complexity measures

[J]. Mechanical Systems and Signal Processing, 2022, 172, 108964.

DOI:10.1016/j.ymssp.2022.108964      [本文引用: 1]

YIN C , WANG Y L , MA G C , et al.

Weak fault feature extraction of rolling bearings based on improved ensemble noise-reconstructed EMD and adaptive threshold denoising

[J]. Mechanical Systems and Signal Processing, 2022, 171, 108834.

DOI:10.1016/j.ymssp.2022.108834      [本文引用: 1]

张迅, 赵宇, 阮灵辉, 等.

基于小波变换分析箱梁振动噪声的时频特性

[J]. 西南交通大学学报, 2020, 55 (1): 109- 117.

URL     [本文引用: 1]

ZHANG X , ZHAO Y , RUAN L H , et al.

Time-frequency characteristics of box-girder vibration and noise based on wavelet transform

[J]. Journal of Southwest Jiaotong University, 2020, 55 (1): 109- 117.

URL     [本文引用: 1]

HUANG N E , SHEN Z , LONG S R , et al.

The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis

[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454 (1971): 903- 995.

DOI:10.1098/rspa.1998.0193      [本文引用: 1]

WU Z H , HUANG N E .

Ensemble empirical mode decomposition: a noise-assisted data analysis method

[J]. Advances in Adaptive Data Analysis, 2009, 1 (1): 1- 41.

DOI:10.1142/S1793536909000047      [本文引用: 1]

DRAGOMIRETSKIY K , ZOSSO D .

Variational mode decomposition

[J]. IEEE Trans.on Signal Processing, 2014, 62 (3): 531- 544.

DOI:10.1109/TSP.2013.2288675      [本文引用: 3]

王奉涛, 柳晨曦, 张涛, 等.

基于k值优化VMD的滚动轴承故障诊断方法

[J]. 振动、测试与诊断, 2018, 38 (3): 540- 547.

URL     [本文引用: 1]

WANG F T , LIU C X , ZHANG T , et al.

Fault diagnosis of rolling bearing based on k-optimized VMD

[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38 (3): 540- 547.

URL     [本文引用: 1]

毕凤荣, 李鑫, 马腾.

基于变模式分解的爆震特征识别方法

[J]. 振动、测试与诊断, 2018, 38 (5): 903-907, 1076.

URL     [本文引用: 1]

BI F R , LI X , MA T .

Knock detection using variable mode decomposition

[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38 (5): 903-907, 1076.

URL     [本文引用: 1]

李华, 伍星, 刘韬, 等.

变分模态分解和改进的自适应共振技术在轴承故障特征提取中的应用

[J]. 振动工程学报, 2018, 31 (4): 718- 726.

URL     [本文引用: 1]

LI H , WU X , LIU T , et al.

Application of variational mode decomposition and improved adaptive resonance technology in bearing fault feature extraction

[J]. Journal of Vibration Engineering, 2018, 31 (4): 718- 726.

URL     [本文引用: 1]

程军圣, 李梦君, 欧龙辉, 等.

FA-PMA-VMD方法及其在齿根裂纹故障诊断中的应用

[J]. 振动与冲击, 2018, 37 (15): 27-32, 67.

URL     [本文引用: 1]

CHENG J S , LI M J , OU L H , et al.

FA-PMA-VMD method and its application in gear tooth root crack fault diagnosis

[J]. Journal of Vibration and Shock, 2018, 37 (15): 27-32, 67.

URL     [本文引用: 1]

唐贵基, 王晓龙.

参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用

[J]. 西安交通大学学报, 2015, 49 (5): 73- 81.

URL     [本文引用: 1]

TANG G J , WANG X L .

Parameter optimized variational mode decomposition method with application to incipient fault diagnosis of rolling bearing

[J]. Journal of Xi'an Jiaotong University, 2015, 49 (5): 73- 81.

URL     [本文引用: 1]

XU B , ZHOU F X , LI H P , et al.

Early fault feature extraction of bearings based on Teager energy operator and optimal VMD

[J]. ISA Transactions, 2019, 86, 249- 265.

[本文引用: 1]

郑圆, 胡建中, 贾民平, 等.

一种基于参数优化变分模态分解的滚动轴承故障特征提取方法

[J]. 振动与冲击, 2020, 39 (21): 195- 202.

URL     [本文引用: 1]

ZHENG Y , HU J Z , JIA M P , et al.

A method for rolling bearing fault feature extraction based on parametric optimization VMD

[J]. Journal of Vibration and Shock, 2020, 39 (21): 195- 202.

URL     [本文引用: 1]

SEYEDALI M , SEYED M , ANDREW L .

Grey wolf optimizer

[J]. Advances in Engineering Software, 2014, 69, 46- 61.

[本文引用: 2]

LI J M , YAO X F , WANG H , et al.

Periodic impulses extraction based on improved adaptive VMD and sparse code shrinkage denoising and its application in rotating machinery fault diagnosis

[J]. Mechanical Systems and Signal Processing, 2019, 126, 568- 589.

[本文引用: 1]

SUN H C , FANG L , ZHAO F .

A fault feature extraction method for single-channel signal of rotary machinery based on VMD and KICA

[J]. Journal of Vibroengineering, 2019, 21 (2): 370- 383.

郑义, 岳建海, 焦静, 等.

基于参数优化变分模态分解的滚动轴承故障特征提取方法

[J]. 振动与冲击, 2021, 40 (1): 86- 94.

URL     [本文引用: 1]

ZHENG Y , YUE J H , JIAO J , et al.

Fault feature extraction method of rolling bearing based on parameter optimization VMD

[J]. Journal of Vibration and Shock, 2021, 40 (1): 86- 94.

URL     [本文引用: 1]

/

〈 〉

京ICP备11035014号-5
版权所有 © 2019 北京航天情报与信息研究所《系统工程与电子技术》编辑部
通讯地址：北京市142信箱32分箱《系统工程与电子技术》编辑部(100854)
电　话：(010)68388406/68386014    E-mail：xtgcydzjs@126.com(系统工程与电子技术)/jseeoffice@126.com(JSEE)
本系统由北京玛格泰克科技发展有限公司设计开发