0 引言
近年来, 随着航空电子产品可靠性不断提高, 额定应力试验产生的故障数据越来越少甚至无故障, 需采用加速试验的方法, 在保持失效机理不变的条件下, 加速产品失效过程, 以减少试验时间, 缩短研制进度。同时, 由于航空电子产品运行环境复杂, 包括工作应力(如电流、电压等)和环境应力(如温度、湿度、振动和冲击等), 导致传统简单应力试验无法真实复现实际工作环境。因此, 需要研究多应力加速寿命评估方法, 准确获取航空电子产品实际使用环境下的寿命数据。
对于在多应力加速试验中获得的试验数据, 需要利用参数估计方法进行数据处理和可靠性指标外推。极大似然估计(maximum likelihood estimation, MLE)提供了一种利用给定观测数据评估模型参数的方法, 被广泛用于估计简单应力下加速模型的未知参数。但多应力模型中参数过多, 多种应力间存在复杂关系, 使得似然函数求解困难, 采用传统计算方法精度不够、效率不高, 甚至无法求解, 因此可以引入智能算法进行计算和参数求解。国内外有许多学者通过智能算法求解参数估计模型, 获取多应力加速模型。Yang等[18-21]结合神经网络、模拟退火、粒子群优化算法、支持向量回归和遗传算法等进行模型求解, 以预估复杂应力下产品的寿命和测量误差。但很多算法均存在计算效率不高, 容易过早收敛导致结果误差极大等问题。
为解决上述问题, 提出一种考虑广义耦合的多应力加速寿命评估方法, 基于失效机理, 结合模糊映射和模糊相关性明确应力的类型和耦合原则。从试验类别出发, 提出4类MLE方法进行参数估计, 与自适应正弦余弦算法(sine cosine algorithm, SCA)相结合, 求解多应力广义耦合加速模型。以某型低频滤波放大器为例, 设计三应力加速试验, 讨论了考虑实际环境应力耦合和不考虑应力耦合的寿命分布偏差, 得出了考虑实际应力耦合的寿命更短, 符合现实预期。同时, 与传统牛顿迭代法对比, 采用多目标自适应SCA可解决MLE的多参数求解困难问题, 并且求解效率更高, 精度控制在5%以内, 验证了所提方法的有效性。
1 考虑广义耦合的多应力加速模型
1.1 基于Arrhenius的多应力广义耦合加速模型
1.1.1 简单应力加速模型
(1) 单应力加速模型
加速寿命模型的本质是用加大应力而不改变失效机理的方法, 加速产品的失效和退化。根据加速寿命试验的结果, 可以推出正常使用状态或降额使用状态下的产品寿命[22]。典型简单应力加速模型如下。
1) 温度加速应力模型
Arrhenius模型起源于化学领域, 现今广泛应用于加速试验模型建模[23], 一般用于描述产品寿命特征量与所施加温度应力之间的关系, 即
式中: η(·)是产品的寿命特性; α0为常数, 称产品系数, 与产品自身失效机理和试验方法有关; Ea为化学反应的激活能; kB是玻尔兹曼常数, 即8.617 eV/℃; T为温度应力, 一般为开尔文温度, 单位为K。
该模型表明寿命与逆反应速率成正比, 为便于进行多应力推广, 温度加速模型可以表示为
式中: X1为等效的温度应力。
2) 湿度加速应力模型
描述湿度作为加速应力时产品的寿命特征与应力水平之间的关系通常有功率湿度模型、指数湿度模型和倒数指数湿度模型[24], 分别可表示为
式中: RH为所采用的电应力水平; λ和n为与失效模式相关的常数。
3) 电流电压加速应力模型
逆幂律模型通常描述电应力作为加速应力时产品的寿命特征量和应力水平之间的关系[23], 一般可表达为
式中: S为所采用的电应力水平; γ为与产品失效模式相关的常数。
(2) 双应力加速模型
基础的寿命-应力模型只涉及一种应力, 这些模型适用于多数加速试验, 但有些试验包含多种加速应力。因此, 必须推广单应力到双应力乃至多应力, 以更好适应工程需要。在单应力的基础上, 可通过建立物理模型、统计外场及试验数据, 获得一些双应力加速模型, 常用的双应力模型有广义Eyring模型和其相关拓展模型。
广义Eyring模型起源于量子力学和统计力学, 表明了各种外部环境因素对化学反应速率的影响, 在寿命评估中常用于描述含有温度和其他应力与寿命指标[23]的关系:
式中: α0, α1, α2, α3为待估系数; X2为非温度应力, 工程应用可省略1/T。同时, 许多学者提出了不同的基于广义Eyring模型的双应力模型, 例如Peck模型、固体断裂Zhurkov模型[23]等。为便于推广, 将Eyring模型简化为如式(2)的形式:
式中: α3X1X2是X2与温度应力之间可能的耦合项, 需要根据实际应力情况判定存在与否, 但应力之间的耦合情况不一定只有简单相乘关系, 因此需要推广具有广义耦合关系的多应力加速模型。
1.1.2 模型前提和假设
(1) 受测产品的寿命分布满足威布尔分布
加速试验一定程度上会使产品的后期失效提前发生, 从而导致恒定故障率的指数分布在加速试验后期偏差过大, 因此失效率随时间递增的威布尔分布更适用于航空电子产品。
在加速寿命试验下, 寿命累积分布函数为
式中: β是形状参数; η是尺度参数, 一般用来衡量产品的寿命指标。
(2) 试验中多应力水平与寿命满足一定关系
在多应力加速寿命试验中, 要确保加速应力水平不会超过产品可承受的最大应力水平。对于威布尔分布, 特征寿命遵循多应力加速模型:
式中: f(·)表示应力与对数寿命指标的关系; S为标准化后的多应力向量, S=(S1, S2, …, SN)。由于应力测量单位的不同, 在多应力情况下可能存在很大差异, 无法进行统一度量。因此, 需要变换应力来统一不同测量单位下应力的关系, 消除测量单位的影响[24]。Si是第i个应力Xi的标准化形式, 可以表示为
式中: Xi0为第i个应力Xi的正常基准应力水平; XiH为第i个应力Xi的加速基准应力水平。则满足Arrhenius模型、逆幂律模型、指数模型的加速应力标准化过程为
式中: S′i为未标准化应力; 温度应力标准化满足Xi(1), 湿度应力和电流应力标准化满足Xi(2), 某些其他应力标准化满足Xi(3)。
(3) 产品的失效机理在应力水平的各种组合下不发生变化。即在加速模型中, 不同加速应力设置情况下, 同一产品的形状参数β相同。
1.1.3 多应力加速模型的建立和推广
基于Arrhenius模型, 提出一种考虑广义耦合关系的多应力加速模型, 模型由单应力项和多应力广义耦合项组成。因此, 根据式(9)对应力进行标准化后, 多应力反应速率关系可表示为
式中: α0, α1, …, αp为未知参数,
对等式(11)两边取自然对数, 转换为如式(8)形式的考虑广义耦合的多应力加速模型:
式中: 应力项表达为
式中: φ为不同应力间的广义耦合关系; φrs为第r和第s个应力间可能存在的广义耦合关系。其他为对应数目应力可能存在的关系, 由于多应力耦合项不一定是应力的单纯相乘关系, 因此引入一种广义表达表示耦合效应。常用函数形式有指数函数和幂函数, 其参数在一定范围变化时, 可以拟合绝大部分统计模型, 广泛用于回归分析和轨迹建模。从而建立广义耦合表达为
式中: φ为广义耦合表达的通用形式; ωk1、ωk2、ωk3为常数, 表示幂次; k=K1+K2+K3, 为该耦合项中施加应力的数目。耦合项需要结合现实工程情况和产品自身失效机理, 考虑综合应力耦合效应进行判定, 具体形式后续可通过模糊相关性计算确定。
1.2 基于模糊映射层次分析的应力确定方法
1.2.1 结构-机理-应力映射层次分析
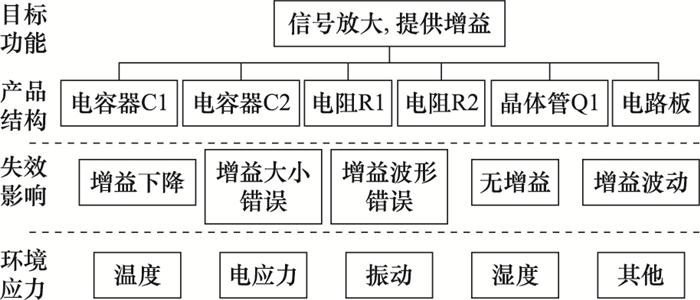
在实际工程应用中, 针对施加应力, 应结合物理失效机理判断应力施加类型和应力耦合项的存在与否。因此, 需分解产品功能结构, 建立可靠性框图[25], 描述产品中所有要素的相互关系, 从而获取功能-结构和失效-应力的映射关系。
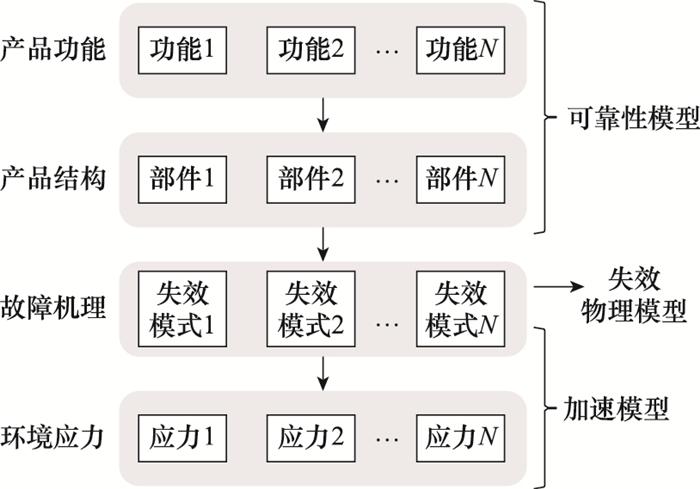
考虑可靠性目标下的层次关系如图 1所示, 其中每层之间的联系相互映射。
图1
图1
功能-结构-失效-应力层次关系
Fig.1
Function-structure-failure-stress hierarchy relationship
1.2.2 基于模糊映射的敏感应力分析
通过层次化映射分析可初步定性获取产品的敏感应力, 为进一步确定实际多应力加速试验的应力类型, 需建立定量模型筛选敏感应力: ①调用失效权重向量、各个故障模式的百分比, 确定模糊关系; ②通过模型获取模糊隶属度, 计算模糊映射矩阵, 确定产品对每种应力的敏感度。
(1) 失效-应力模糊关系表示
构造失效-应力模糊映射关系如下: 直积空间X(=应力)×Y(=失效模式), 映射
式中:
(2) 模糊隶属度和应力敏感度计算
每种应力类型对应的模糊映射定义为
式中: i=1, 2, …, m, 表示应力类型; j=1, 2, …, n, 表示被检测产品的失效模式;
根据第1.2.1节, 定义每种故障模式的故障原因分别为疲劳、磨损、结构破坏、腐蚀等K类, 每种故障原因由s(s≤m)个应力导致, 则第j个故障模式的第i个应力的隶属度为
式中: 第j个故障模式的故障原因百分比为cjk; 第k个故障原因的应力影响程度由影响系数lsk表示。
定义第s个应力的敏感度为Rs(s≤i), 即
式中: λj为第j个失效模式占产品总失效的比例, 即失效模式百分比。应力敏感度可以定量应力对产品的影响程度, 从而确定在多应力加速试验中施加应力的类型。
1.3 基于模糊相关性的广义耦合项计算方法
1.3.1 考虑综合应力耦合效应的耦合项确立
图2
图2
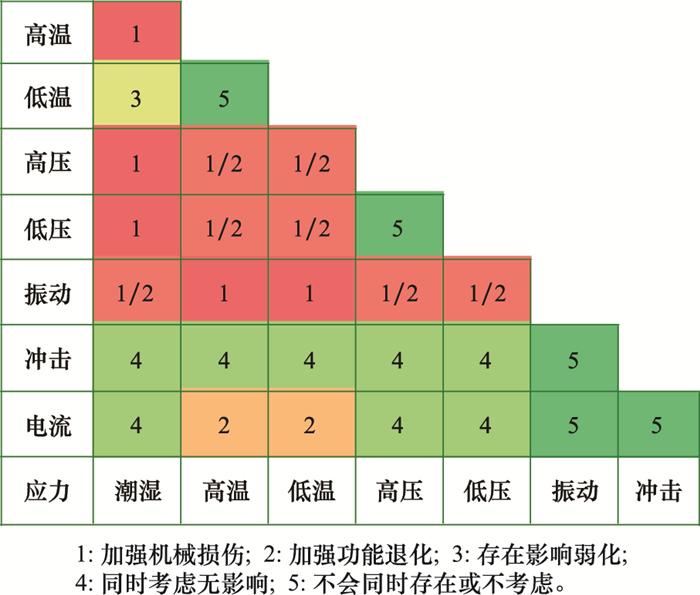
加速应力中的综合应力耦合效应示例
Fig.2
Example of comprehensive stress coupling effects in accelerated stress
1.3.2 考虑广义耦合的多应力加速模型的模糊表示
由于试验观测等存在随机不确定性, 模型建立等存在认知不确定性, 为消除不确定性对耦合项系数的影响, 采用模糊数来表达施加应力与寿命指标的关系。模糊数包括几种类型, 如区间值数、三角数、梯形数、指数等[28]。这里采用最常用模糊化方法, 即三角模糊法, 其隶属函数为
因此, 考虑广义耦合的多应力加速模型的模糊表达为
结合试验数据和模糊相关度计算, 可确定具体的应力广义耦合项的表达形式。
1.3.3 应力耦合关系的模糊相关度计算
相关度衡量样本中两个随机变量是否线性相关, 为确定广义耦合多应力加速模型, 需要计算不同形式耦合项与寿命指标的相关性。传统皮尔森相关系数用来估计一定量实数样本参数之间的相关性, 不适用于模糊数据, 因此提出一种衡量应力与寿命指标模糊相关性的系数计算方法。
对于加速试验获取的寿命数据, 必须考虑模糊区间的长度是否相同, 若将重心和模糊区间长度以相等的权重组合, 则组合可能会超过1或-1, 不满足相关度定义。因此, 为获得合理的模糊相关性, 本文定义所有应力耦合项φ为样本X, 寿命指标ln η为样本Y, 两变量的模糊相关度ε为
其中:
式中: 每组样本的模糊数为xi和yi, 数据长度以模糊隶属面积衡量, 定义为模糊面积||xi||和||yi||; 由此表达模糊重心为(cxi, cyi), 面积为||xi||=area(xi)、||yi||=area(yi)。
同时, (β1, β2)是一个模糊概念, 用来衡量模糊重心和面积的权重, 为简单起见可采用(0.9, 0.1)、(0.8, 0.2)、(0.7, 0.3)、(0.6, 0.4)等来表达权重比例, 从而解释两个变量间相关性的变化。本研究认为重心权重更高, 因此应用(β1, β2)=(0.7, 0.3)来计算模糊数的相关系数。
在模糊相关度的定义下, ε越接近1, 正关联越强, 两个变量越模糊正相关; 反之ε越接近于-1, 负关联越强, 两个变量越模糊负相关; 当ε接近0时, 两个变量几乎不相关。从而通过模糊相关性选取最相关广义耦合项, 以获取与实际情况最符合的形式。
综合第1.2节和第1.3节可得基于失效机理的多应力耦合加速试验的施加应力类型和模型耦合项确立判定流程。
2 考虑广义耦合的多参数估计方法
在实际工程试验中, 一般获取的失效寿命数据有随机截尾数据、全数样本数据、定时截尾数据和定数截尾数据[22]。因此, 从方法的通用性出发, 提出了基于多应力广义耦合加速寿命多种样本数据的MLE方法。
2.1 考虑不同试验数据类型的MLE法
2.1.1 基于多应力广义耦合加速的MLE
(1) 完全样本试验
完全样本试验指样本全部失效才停止试验, 这种试验可获得较完整的数据, 统计分析结果也较好, 但所需时间较长。完全样本试验中, 有n个试验样本, 试验到所有器件全部失效tn时刻停止试验, 依照失效时间先后记录, 试验停止前的失效时间为t1, t2, …, ti, …, tn, MLE为
拓展到多应力的情况, 共设计q组多应力试验, 在第h组试验中, 试件有nh个, 失效时间可表示为th1, th2, …, thi, …, thnh(h≤q), 则多应力组合Sh下产品失效的对数似然函数为
将式(24)代入多应力广义耦合加速模型后, 即可拓展到多应力广义耦合的情况, 获得在完全样本下所有应力组合Sh={S1, S2, …, Sq}下的极大似然函数:
其中, ln ηh(α0, α1, …, αp)为第h组应力组合下的广义耦合加速模型。
(2) 随机截尾试验
随机截尾试验中, 有n个试验样本, r个样本失效, c个样本未失效, 但中途撤离试验, 称为删失样本, n=r+c, 失效时间为t1, t2, …, tr, 删失时间为τ1, τ2, …, τc。则似然函数为
拓展到多应力耦合的情况中, 试件的失效时间和删失时间可分别表示为th1, th2, …, thrh和τh1, τh2, …, τhch, 且nh=rh+ch。
过程同完全样本试验, 式(26)两边取对数, 代入多应力模型, 即可获得在随机截尾试验下多应力广义耦合加速模型的极大似然函数:
(3) 定时截尾和定数截尾试验
定时截尾试验中, 有n个试验样本, 试验到t0时刻停止试验。依照失效时间先后记录试验停止前的失效时间为t1, t2, …, tr≤t0(r < n), 则极大似然函数为
拓展到多应力情况, 试验到th0时刻停止试验, 最后一次记录时间为thr, 且thr≤th0。则多应力组合下产品失效的对数似然函数可表示为
将式(29)代入多应力耦合加速模型, 得定时截尾试验下, 所有应力组合的极大似然函数模型为
同理, 在定数截尾试验中, 试验到第rh个试验件失效后停止试验, 时间为thr。则与定时截尾试验类似, 极大似然函数可表示为
2.1.2 多应力广义耦合MLE模型总结
综合上述4种数据截尾方式, 可得不同截尾试验下的MLE通用模型为
其中, A、B、C、D的形式如表 1所示。
表1 通用多应力MLE模型各相取值
Table 1
| 数据类型 | A | B | C | D |
| 完全样本 | nh | |||
| 随机截尾 | rh | |||
| 定时截尾 | rh | |||
| 定数截尾 | rh |
2.2 求解多应力模型参数的自适应SCA
由于模型参数过多, 使用传统方法过程繁琐、计算量大、求解困难, 所得参数估计模型的误差较大, 置信度不足。因此, 引入多目标自适应SCA, 解决多应力广义耦合情况下传统方法难以求解的问题, 同时在一定程度上减小误差。
2.2.1 建立多参数MLE优化模型
传统似然函数进行MLE时, 对每个待求参数求偏导, 得到一组非线性方程组, 求解较为困难。因此, 在多参数似然函数的求解过程中, 为提高对模型参数求解效率, 将问题转化为优化算法解决多参数无约束优化问题。
一般优化算法的核心是构造自适应变量目标, 针对非线性参数求解问题, 可以采用令每一个方程的绝对值尽量靠近0的方法来进行多参数优化求解。得到自适应目标后, 可以进行优化迭代, 来最小化目标并找到根, 如下所示:
算法目的即转化成寻找无约束优化模型的最小值Fmin, 建立多参数MLE优化模型, 解决非线性求解困难问题。
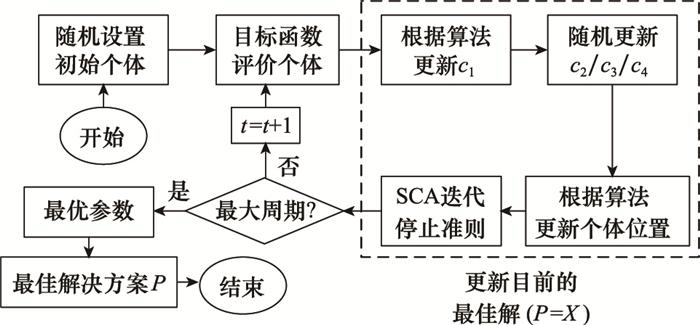
2.2.2 自适应多目标SCA
图3
(1) 自适应过程控制
为探索和利用之间取得适当的平衡, 以实现全局最优解。SCA进行自适应调整和迭代, 如下所示:
式中: t是当前迭代的次数; T是最大迭代次数; b是常数值。c1控制全局搜索和局部探索的转化, 当c1较大时进行全局搜索, 较小时进行局部探索。
(2) 局部探索控制
正余弦函数在[-2, 2]内的影响用数学模型sin c2和cos c2来表示, 该模型描述了正余弦函数的切换范围需要一个解来更新其在不同解中的位置。因此, 定义c2∈[0, 2π], 以搜索局部空间内外的随机位置, 实现局部探索。
(3) 更新个体位置
为了更新参数估计和迭代的位置, 使用等式更新最优解:
式中: Pij表示当前解在第j次迭代时在第i维的位置; c1, c2, c3, c4是4个随机数; Qij是目标位置, 绝对值表示幅度; 参数c1表示向下一个位置区域的移动方向; 参数c2在[2, 2π]之间, 表示运动应该朝向或远离目标的程度; 参数c3表示目标的随机权重分数, 以随机强调(c3>1)或淡化(c3 < 1)目标在确定距离方面的影响; 参数c4是[0, 1]之间的随机数, 表示正弦和余弦函数之间的切换。
(4) 迭代停止
通过一组初始随机解开始优化过程, 然后缓存迄今为止获得的最佳解决方案, 将其指定为目标点, 并在考虑所选最佳解决方案的同时更新其他解决方案。随着迭代次数的增加, 正弦和余弦函数的范围被刷新以保持对搜索空间的利用。当迭代次数达到最大迭代次数时, 停止优化过程。
通过上述过程, 可以获取多应力耦合MLE模型的未知参数, 从而进行寿命评估。
3 实例分析
3.1 多应力耦合加速寿命评估方法整体思路
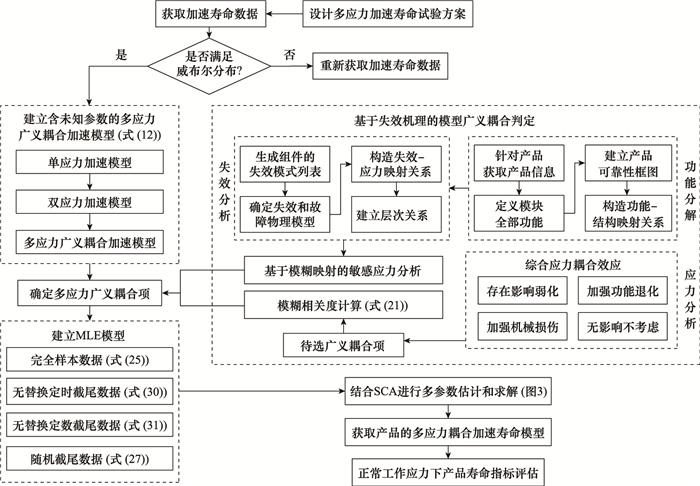
提出基于多应力广义耦合的加速寿命评估方法, 包括三大步骤: ①建立对应含未知参数的多应力广义耦合加速模型, 并确定敏感应力和广义耦合项形式; ②根据不同试验数据类型建立多参数估计模型, 并结合SCA进行参数求解; ③基于加速模型外推正常工作应力下产品的寿命指标。整体思路如图 4所示。
图4
3.2 试验和寿命评估案例分析
3.2.1 试验对象分析
以民用机载电子设备中的射频低噪声放大模块为对象, 进行加速寿命评估和分析。
首先, 进行模糊映射层次分析和敏感应力确定, 确定试验方案, 进行结构-机理-应力的映射分析, 结果如图 5所示。
图5
图5
低噪声放大模块功能-结构映射关系
Fig.5
Function-structure mapping relationship of low-noise amplification module
从可靠性预计手册和外场相似产品数据处获取失效模式和数据, 在工程实际中, 一般采用故障模式、机理及影响分析(failure modes, mechanisms and effects analysis, FMMEA)建立映射关系矩阵。
本文FMMEA结果参考文献[22], 调用该低噪声放大模块各个故障模式的百分比和失效率, 通过结合先验信息和第1.2.1节中的方法, 计算模糊隶属度, 获取失效机理-环境应力模糊映射矩阵:
最终, 计算得施加的敏感应力结果如表 2所示, 为便于工程试验, 选择施加电流、温度和湿度。
表2 低噪声放大模块敏感应力分析结果
Table 2
| 应力 | 应力敏感度 |
| 温度 | 0.319 2 |
| 湿度 | 0.225 8 |
| 电应力 | 0.384 4 |
| 振动 | 0.223 5 |
| 其他 | 0.100 5 |
3.2.2 广义耦合加速模型建模
考虑综合应力耦合效应, 对于电子元器件和电路板, 在高温高湿条件下, 高温加速水汽渗透使电路板表面离子的活性增强, 强化化学腐蚀和电化学效应, 高温下电子活性增强, 同时电子元器件对温度敏感, 工作电流存在浮动和变化[25], 存在耦合关系; 但在潮湿情况下加大电流应力, 一般不会加快损伤或退化进程, 认为不耦合。
因此, 在该三应力试验中, 设置应力耦合关系如表 3所示。
表3 三应力耦合项及系数设置
Table 3
| 加速应力项 | 系数 |
| S1 | α1 |
| S2 | α2 |
| S3 | α3 |
| φ12 | α4 |
| φ13 | α5 |
| φ23 | 0 |
| φ123 | 0 |
根据加速模型, 考虑实际情况耦合和不考虑耦合的三应力加速模型分别为
为便于工程计算, 基于试验结果对所有3次方以下的备选模型进行模糊相关性分析, 备选结果如表 4所示。
表4 广义耦合项的最佳备选形式和模糊相关性
Table 4
| φ12表达式 | ε | φ13表达式 | ε | |
| 0.838 7 | S1exp(S3) | 0.995 2 | ||
| 0.836 1 | 0.992 9 | |||
| S1exp(S2) | 0.820 7 | S12S32 | 0.989 6 | |
| S12S22 | 0.814 0 | exp(S1)exp(S3) | 0.988 7 | |
| S1S2 | 0.805 3 | S1S3 | 0.978 0 |
最后, 确定最优广义耦合项形式为
备选广义耦合项和传统简单耦合项形式分别为
3.2.3 加速试验设计
三应力试验的每个应力组合下的试件数量为20个, 直到所有产品全部失效。该产品的正常工作温度、湿度和电流要求分别为30℃, 50%, 10 mA, 即该组实验的标准法向应力水平。在加速试验中, 施加应力水平如表 5所示。
表5 三应力加速寿命试验方案
Table 5
| 试验应力组合 | 应力水平和组合 | 件数 | ||
| 温度/℃ | 湿度/% | 电流/mA | ||
| 1 | 80 | 80 | 20 | 20 |
| 2 | 80 | 80 | 60 | 20 |
| 3 | 55 | 80 | 40 | 20 |
| 4 | 55 | 95 | 20 | 20 |
| 5 | 70 | 95 | 60 | 20 |
| 6 | 70 | 95 | 40 | 20 |
在三应力试验中投入120件产品, 按评估方案分为6组, 进行定数截尾试验, 直到产品失效截止试验, 统计相关失效数据。
3.2.4 数据的统计分析和假设检验
图6
表6 三应力试验数据AIC和BIC检验结果
Table 6
| 分布 | AIC | BIC |
| 威布尔 | 661.673 0 | 680.185 4 |
| 对数Logistic | 682.314 8 | 700.827 2 |
| 对数正态 | 691.632 6 | 710.145 0 |
| Logistic | 747.858 1 | 766.370 5 |
| 正态 | 905.707 1 | 924.219 5 |
| 最小极值 | 918.994 2 | 934.975 8 |
| 最大极值 | 929.897 0 | 948.409 5 |
| Frechet | 957.679 5 | 976.191 9 |
| 指数 | 981.523 99 | 1 000.036 4 |
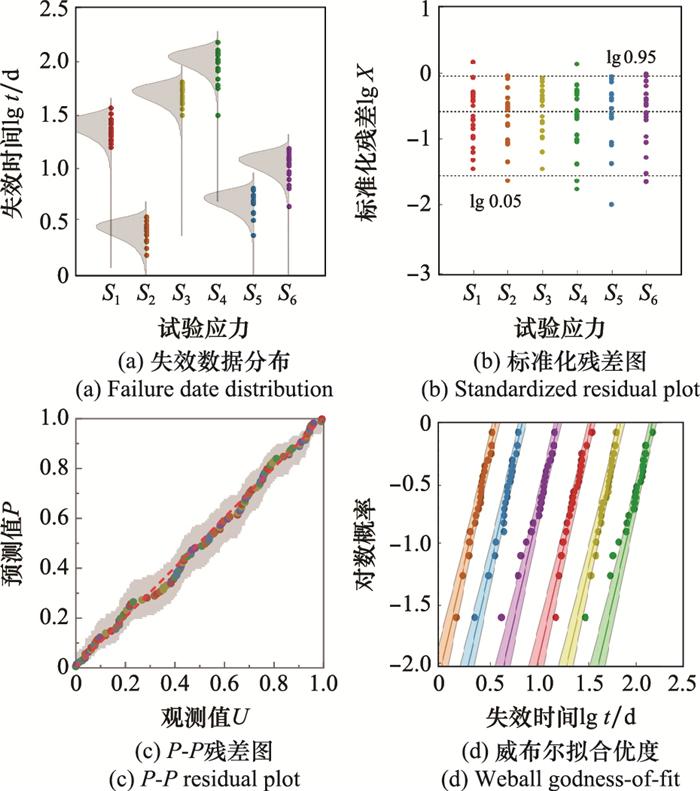
同时, 分别对6组试验数据进行K-S检验, 个案数为20, 原假设显著性水平p0=0.05, 检验结果如表 7所示。
表7 三应力试验数据K-S检验结果
Table 7
| 试验序号 | 平均值 | 标准偏差 | 显著性水平 |
| 1 | 24.214 6 | 5.369 9 | 0.980 5 |
| 2 | 2.665 6 | 0.555 7 | 0.863 0 |
| 3 | 49.896 7 | 9.110 4 | 0.704 0 |
| 4 | 97.884 9 | 28.851 9 | 0.789 2 |
| 5 | 4.951 6 | 1.037 9 | 0.377 0 |
| 6 | 10.973 1 | 2.918 3 | 0.740 0 |
结果表明, 6组数据的显著性水平均大于0.05, 所以接受原假设。通过拟合优度综合判定, 试验数据最满足威布尔分布, 可以进行模型建模、参数估计和寿命评估。
3.2.5 基于SCA的多参数估计和寿命外推
根据式(33)得到MLE模型, 通过SCA和传统牛顿迭代法求解待求参数。
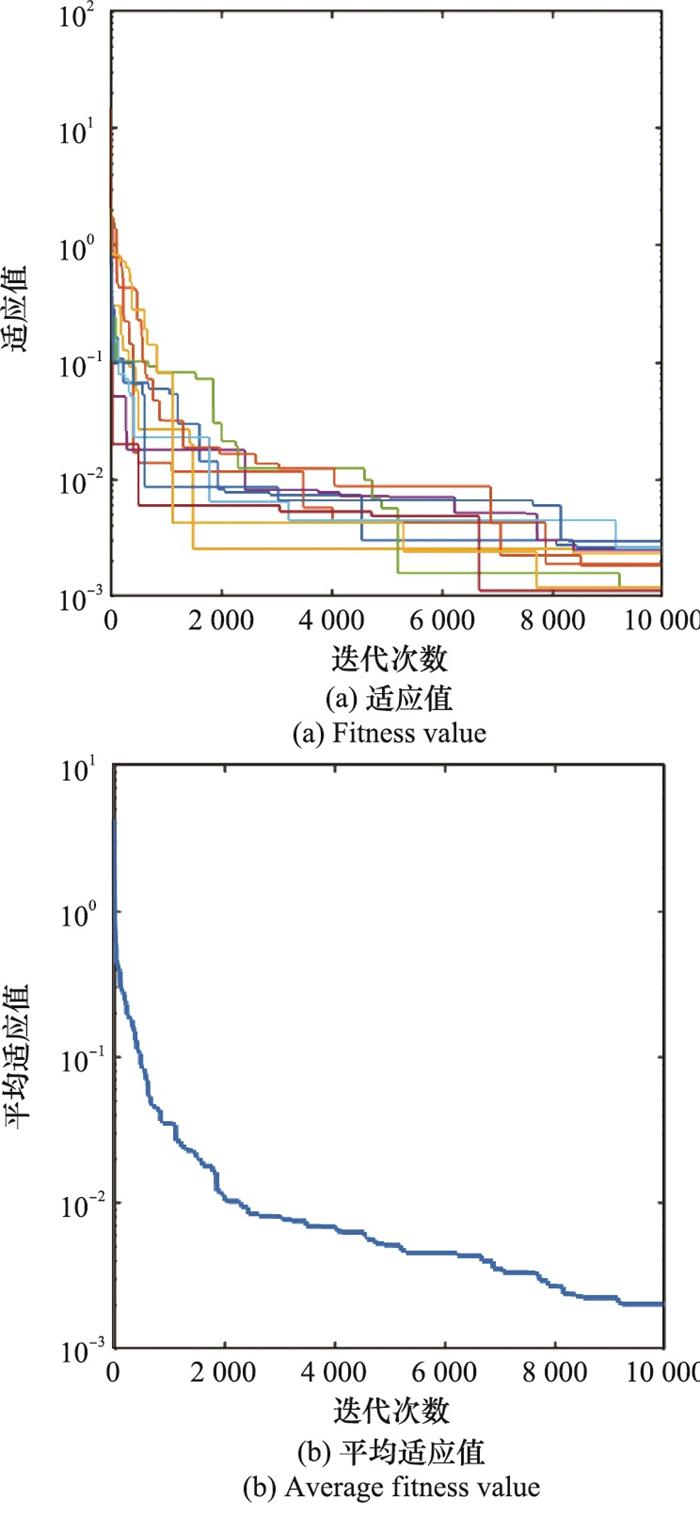
设置算法参数为N=50, a=2, Tmax=10 000;搜索空间设置为[-12, 12]。为尽量消除随机数的影响, 进行10次迭代运算, 计算其平均值。图 7给出了三应力最优广义耦合参数求解的所有适应值收敛曲线和平均适应值收敛曲线, 10 000次迭代后平均适应值收敛于1.93×10-3, 表明该方法求解模型具有良好的迭代收敛性。
图7
图7
三应力最优广义耦合参数求解迭代收敛曲线
Fig.7
Iterative convergence curve for solving triple-stress optimal generalized coupling parameters
表8 三应力模型自适应SCA值、牛顿迭代MLE值及MSE
Table 8
| 模型 | 待求参数 | SCA | 牛顿迭代法 | MSE/% |
| 最优广义耦合 | lnα0 | 8.031 5 | 8.081 6 | 4.361 7 |
| α1 | 1.117 6 | 1.119 1 | 4.908 0 | |
| α2 | 0.759 4 | 0.828 2 | 1.905 2 | |
| α3 | 1.350 7 | 1.232 7 | 4.406 5 | |
| α4 | 0.966 8 | 0.954 5 | 3.428 1 | |
| α5 | 1.130 6 | 1.177 8 | 2.429 0 | |
| 传统简单耦合 | lnα0 | 8.416 6 | 8.443 8 | 3.025 6 |
| α1 | 2.116 4 | 2.297 3 | 3.016 6 | |
| α2 | 1.615 5 | 1.677 8 | 0.943 5 | |
| α3 | 0.288 2 | 0.276 7 | 0.740 2 | |
| α4 | -0.605 1 | -0.606 6 | 0.401 2 | |
| α5 | 3.984 1 | 3.992 1 | 2.701 6 | |
| 备选广义耦合 | lnα0 | 7.945 9 | 7.882 4 | 2.528 2 |
| α1 | 3.824 1 | 3.862 8 | 2.728 2 | |
| α2 | 0.085 7 | 0.086 7 | 2.214 2 | |
| α3 | 3.276 0 | 3.171 5 | 2.291 7 | |
| α4 | -0.405 1 | -0.429 4 | 2.587 7 | |
| α5 | 0.274 1 | 0.277 9 | 1.062 2 | |
| 应力不耦合 | lnα0 | 10.117 8 | 10.121 3 | 2.633 4 |
| α1 | 4.517 8 | 4.526 2 | 0.856 0 | |
| α2 | 1.635 3 | 1.580 4 | 2.415 7 | |
| α3 | 2.788 0 | 2.848 7 | 1.091 8 | |
| α4 | - | - | - | |
| α5 | - | - | - |
表9 威布尔分布的三应力参数估计值和标准误差
Table 9
| 应力组合 | 参数 | 估计值 | 标准误差 | 置信区间(95%) | |
| 1 | η1 | 26.470 8 | 1.157 1 | (24.364 9, 28.997 5) | |
| 2 | η2 | 2.865 8 | 0.124 4 | (2.640 3, 3.138 9) | |
| 3 | η3 | 52.751 5 | 2.284 2 | (48.639 0, 57.794 6) | |
| 4 | η4 | 110.386 7 | 4.826 1 | (101.597 9, 120.923 7) | |
| 5 | η5 | 5.295 3 | 0.229 5 | (4.881 4, 5.801 3) | |
| 6 | η6 | 12.132 1 | 0.528 2 | (11.174 1, 13.290 2) | |
| 整体 | β | 5.185 8 | 0.376 4 | (4.475 1, 5.950 3) |
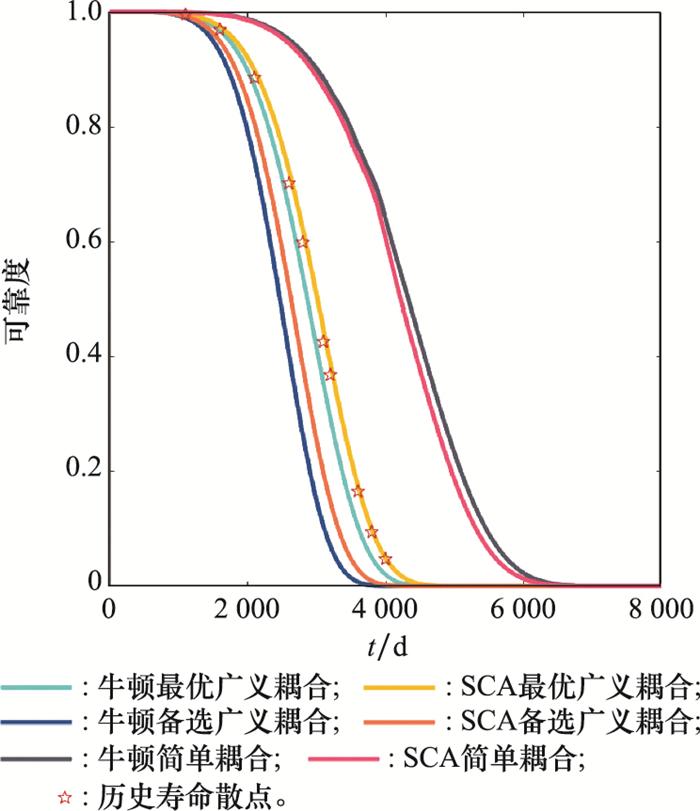
最后, 可以通过求解出的多应力耦合模型外推在正常应力水平下的寿命指标, 给出了最优广义耦合模型、备选广义耦合模型、传统简单耦合模型的牛顿迭代法和自适应SCA的寿命估计结果, 并与可靠性预计中的历史寿命进行对比, 结果如图 8所示。
图8
如表 10所示, 针对该低噪声放大模块, 进行三应力加速试验, 分别对比3类考虑应力耦合和应力不耦合的模型求解结果, 考虑应力广义耦合作用的结果更贴近于实际预计情况, 且经模糊相关性分析的最优广义耦合模型最满足历史寿命数据。根据先验信息, 该产品预计寿命约为3 200天, 与历史经验寿命数据相比, 不考虑应力间耦合结果存在较大误差, 由此可得出应力间的耦合作用对该产品寿命估计精度有很大影响, 必须考虑实际耦合作用。同时, 基于自适应SCA的多参数估计方法标准误差均在5%以内, 说明了参数预测的准确。
表10 正常应力下寿命评估结果
Table 10
| 三应力模型 | SCA | 牛顿迭代法 | 平均相对误差 |
| 最优广义耦合 | 3 076.42 | 3 234.27 | -0.014 0 |
| 备选广义耦合 | 2 823.86 | 2 650.10 | -0.144 7 |
| 传统应力耦合 | 4 521.51 | 4 646.02 | 0.432 4 |
| 不考虑应力耦合 | 24 780.65 | 24 867.15 | 6.757 5 |
4 结束语
本文提出一种多应力广义耦合加速寿命评估方法, 结合实际航空电子产品复杂运行环境, 首先基于传统加速应力模型, 推导出一种考虑多应力广义耦合的加速模型描述分布参数与应力水平的关系, 并基于模糊映射和模糊相关性, 结合产品和工程应用实际给出广义耦合项的设置判定方法, 为长寿命产品的寿命评估提供理论基础。其次, 提出不同试验数据类型的多应力广义耦合参数MLE方法, 并采用自适应SCA获取未知参数, 解决多应力加速模型多参数估计难题。然后, 以某型低噪声放大模块为例, 对方法的正确性和有效性开展验证, 经验证该方法更贴近于实际工作环境且误差控制在5%以内, 有效解决无法快速准确获取国产航空电子零部件的寿命指标问题。
在小样本和数据缺乏的情况下对样本数据的质量要求较高, 小样本容错率较小; 由于自适应算法的随机性, SCA有可能出现结果偏差较大的问题, 需要进行多次迭代求解。后续有待于对其中存在的不确定性和随机性问题进行进一步的研究和探讨。
参考文献
基于多应力综合加速模型的产品可靠性评估方法
[J].
A product reliability evaluation method based on multi-stress comprehensive acceleration model
[J].
加速寿命试验中多应力加速模型综述
[J].
Review of multiple-stress models in acce-lerated life testing
[J].
双应力恒加寿命试验下相依竞争失效模型的统计分析
[J].
Statistical analysis of dependent competitive failure model under double stress constant stress life test
[J].
Reliability assessment model considering heterogeneous population in a multiple stresses accele-rated test
[J].
A new universal multi-stress acceleration model and multi-parameter estimation method based on particle swarm optimization
[J].
基于D优化的多应力加速退化试验设计
[J].
Multi stress accelerated degradation test design based on D optimization
[J].
A novel accelerated life-test method under thermal cyclic loadings for electronic devices considering multiple failure mechanisms
[J].
Accelerated life test of high luminosity blue LEDs
[J].
Reliability and remaining life assessment of an electronic fuze using accelerated life testing
[J].
Optimal design of constant stress accelerated degradation test plan with multiple stresses and multiple degradation measures
[J].
多应力耦合条件下氧气浓缩器退化建模
[J].
Degradation modeling of oxygen concentrator under multiple stress coupling condition
[J].
基于模糊层次分析法的系统加速验证试验设计
[J].
System-level accelerated reliability demonstration testing design based on fuzzy logic and AHP
[J].
A random fuzzy accelerated degradation model and statistical analysis
[J].
An approach to system reliability analysis with fuzzy random variables
[J].
On reliability estimation based on fuzzy lifetime data
[J].
A non-li-near fuzzy regression for estimating reliability in a degradation process
[J].
Bayesian reliability analysis for fuzzy lifetime data
[J].
Smart electricity meter reliability prediction based on accelerated degradation testing and modeling
[J].
Reliability modeling and a statistical inference method of accelerated degradation testing with multiple stresses and dependent competing failure processes
[J].
基于CK-GPR的多应力环境智能电表剩余寿命预测
[J].
Remaining useful life prediction of smart meter based on CK-GPR in multi-stress environment
[J].
基于BP神经网络的多应力加速寿命试验预测方法
[J].
Life-prediction of multi-stress accelerated life testing based on BP algorithm of artificial neural network
[J].
Accelerated life testing-step-stress models and data analyses
[J].
Reliability estimation considering multi-stress monotonic degradation test data with non-constant scale parameter
[J].
Potential failure mode identification of operational amplifier circuit board by using high accelerated limit test
[J].
SCA: a sine cosine algorithm for solving optimization problems
[J].
A new statistical inference method for multi-stress accelerated life testing based on random variable transformation
[J].