0 引言
海洋因其固有的多变性和不均匀性, 导致水声信道是最为复杂多变的无线通信信道之一, 面临多途扩展严重、频带资源有限、时延长的问题[1-2]。近年来, 随着国家“智慧海洋”战略的推进, 以及海洋资源开发, 基于水下传感器网络的水声应用提出了自适应通信的需求[3-4]。但由于水声信道的特性, 当水下传感器源节点直接与汇聚节点通信时, 存在丢包率高、中断率高、可靠性差的问题[5]。Meulen和Cover等[6-7]首先提出协作通信的理念, 通过在源节点和汇聚节点之间加入中继节点协作通信, 有效增加链路可靠性[8-9]。正交频分复用(orthogonal frequency division multiplexing, OFDM)是一种多载波调制方法。通过频分复用实现高速串行数据的并行传输, 是一种有效对抗频率选择性衰落的通信技术[10-12], 在水声通信领域成为了重点发展对象。文献[13-15]提出在OFDM通信制式各子载波间的衰落特性差异很大的情况下, 发射端利用反馈的信噪比(signal to noise ratio, SNR)或误码率参数进行不同速率的自适应切换, 这种基于接收SNR或误码率的自适应传输方案虽然简单可行, 但仅反馈信道状态信息(channel state information, CSI)的某一关键参数, 无法准确描述衰落信道的统计特征。
Liu等[22]利用卷积神经网络和长短期记忆的继成网络设计了一种在线CSI预测模型, 预测性能在多址接入系统中表现了较强优势。Wang等[23]提出一种通过将节点视为智能代理, 节点网络视为多代理网络的方法, 将智能控制中的强化学习概念引入水声传感器网络(underwater acoustic sensor network, UASN), 通过划分状态空间和动作空间, 作者提出了一种基于协作Q-Learning的分布式资源分配算法。该算法通过实验验证了在传输容量指标上优于其他算法。文献[24]建立了捕获未知环境参数对信道质量影响的随机模型, 并提出利用隐马尔可夫模型来补充稀疏信道测量, 预测跨越多天的长时间内的信道特征。现有的基于卷积神经网络、强化学习方法或隐形马尔可夫链的方法虽然能够较好预测信道, 克服瞬时CSI的过时问题, 但该类方法往往需要长期的观测和大量的训练样本, 在水下应用中通常难以满足。文献[25-27]提出利用CSI二阶统计的长期稳定性, 推导出不完美的CSI概率密度函数, 由此表征实际信道情况, 在计算复杂度低的情况下获得了较高比特率。
基于以上问题, 本文提出一种基于不完美CSI的水声自适应功率分配算法(underwater acoustic adaptive power allocation algorithm based on imperfect CSI, APAIS), 首先构建基于中继协作OFDM通信的水下传感器网络模型, 中继节点采用放大转发的方式, 在接收到源节点发送的信号后, 将功率线性放大, 在随后的时隙传递给目的节点。利用Bellhop模型进行水声信道建模, 通过输入实验仿真参数可以得到多径数目、幅度和时延等信息, 进而可以给出信道的冲激响应, 为后续的自适应通信做准备。针对如何在不完美的CSI下进行自适应通信问题, 本文提出了利用条件概率模型表征CSI的不完美问题, 并由此推导出传输时的理论CSI。然后借助于CSI条件概率密度, 可基于不完美CSI获得较为理想的资源分配方案。
1 系统模型
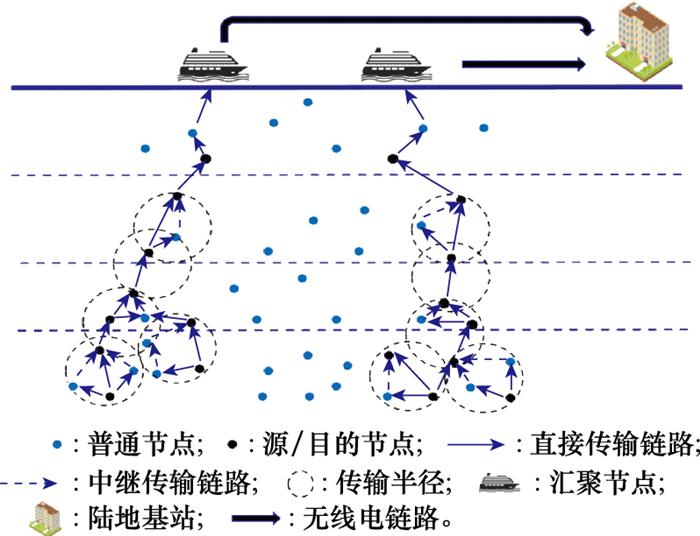
水下传感器网络采用分层结构, 最底层的传感器节点被任意锚定在水下传感网中, 具备一定的感知能力, 执行采集信息任务, 并搭配了水声通信模块进行节点通信, 由于海底生物种类复杂, 需要收集的信息繁多, 因此在最底层部署较多传感器。其他传感器均匀部署在每层, 中继节点也执行信息收集任务, 并负责转发终端感知节点传递过来的数据包, 最终将其发送到sink节点处。水下采用水声通信, 水面采用无线电通信的方式, 将数据传输到陆地基站,如图 1所示。
图1
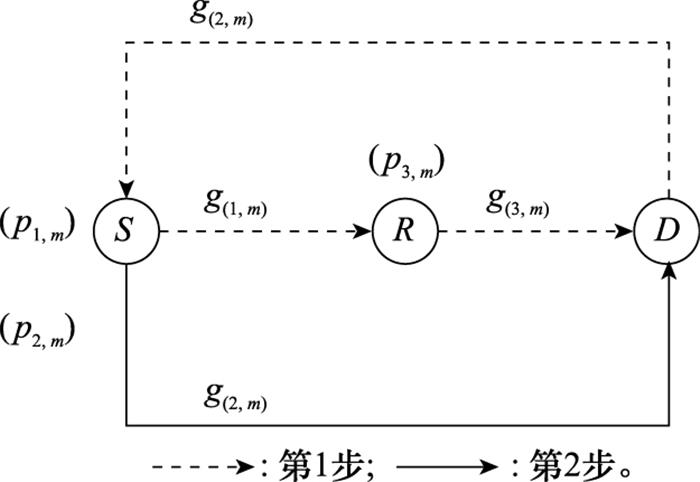
水下传感器节点不仅执行日常信息收集的任务, 还参与协作通信的中继转发任务, 本文采用在水声通信中应用较为广泛的三节点两跳中继模型: 1个源节点、1个中继节点、1个目的节点。为防止发送信号对接收信号产生干扰, 中继端采用时分半双工方式通信,如图 2所示。第1个时隙中, 中继节点接收源节点发送的信号, 源节点可以直接向目的节点通信。第2个时隙中, 经中继处理后的信号转发给目的节点, 同时源节点再次向目的节点发送数据包。
图2
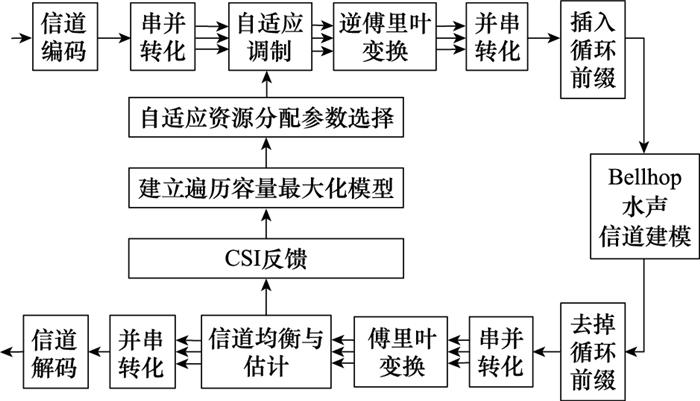
OFDM自适应水声通信模型如图 3所示, 先使用低SNR模式下二进制相移键控(binary phase shift keying, BPSK)发送一次数据, 对接收数据进行信道估计, 将估计得到的时域信道冲激响应作为CSI的已知条件[28], 考虑导致CSI不完美的因素, 推导出条件概率特征的信道增益, 并利用所得到的条件概率密度函数进行遍历容量最大化建模, 根据容量最大化原则, 发送端根据接收到的CSI为子载波选择合适的调制模式、分配发送功率比特。本文基于OFDM的自适应通信系统的实现过程包括以下3个关键部分: ①条件概率表征不完美的CSI[29]; ②建立遍历容量最大化模型; ③自适应资源分配通信参数的选择。
图3
2 APAIS算法
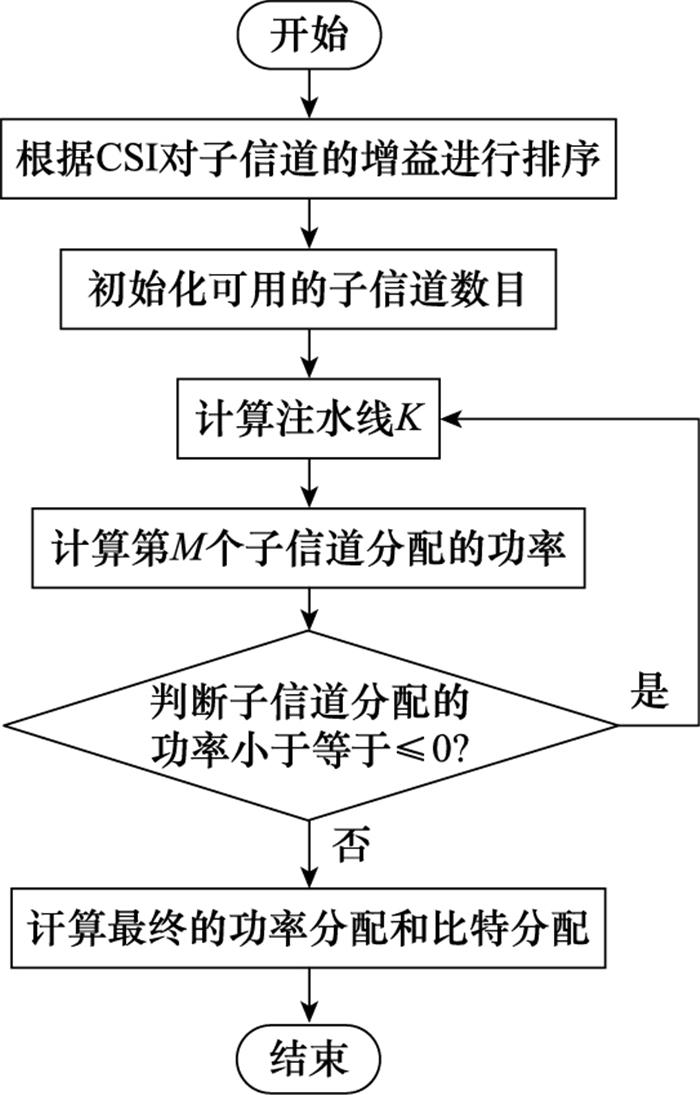
本文基于以上系统模型, 考虑水声信道中多径效应和多普勒扩展等因素对自适应资源分配性能的影响, 自适应功率和比特分配流程图如图 4所示。首先发射端针对接收端反馈回的CSI对各子信道增益进行排序, 并初始化可用的子信道数目, 通过计算注水线分配每个子信道的功率。本文考虑到某些信道具有严重的频率选择性衰落时可能会出现分配的功率为负值的情况, 所以加入对子信道功率正负值的判断, 当系统的总功率不能满足所有子信道的分配, 应该放弃信道状况最差的信道, 不给其分配功率, 此时需要重新计算注水线, 直至所有的信道分配的功率非负。
图4
2.1 中继协作通信
考虑如图 1所示的水声中继放大(amplify and forward, AF)协作OFDM系统模型, 中继节点采用半双工模式, 不能同时收发信息, 避免自干扰导致的通信质量下降问题。为了简化本文所提模型, 提高模型的通用性, 本文假设源节点在两个时隙内发送相同码元。其中, 中继节点的工作模式可分为两步。
第1步, 待传输的信息被编码成m个独立复数符号Sm~CN (0, 1), 并分配给m个子载波, 假设源节点传输Sm至中继节点和目的节点的总功率为p1, m, 上述两节点对应的接收信号为
式中: n1, m~CN(0, ε12)和n2, m~CN(0, ε22)为两节点各自的加性高斯白噪声, 功率为ε12和ε22。本文假定其余各子载波在两节点处的加性高斯白噪声功率均为ε12和ε22。
第2步, 中继节点先将接收信号r1, m进行功率放大, 并以功率p3, m将放大信号转发到目的节点, 且设定功率放大系数为am·exp(jθm), 其中am和θm分别表示幅度放大系数和相位转发系数, 其值分别如下:
式中: ∠(·)表示上述信号的相位信息; 幅度am的取值确保中继节点以p3, m传输信号, 相位的取值保证在目标节点处由直达链路传输的信号和由中继节点传输的信号能保持相同相位。与此同时, 源节点也会在直达链路上继续以p2, m功率传输信号Sm。第2时隙目标节点接收的信息为
基于上述通信过程, 目标节点在第m个子载波上的第1和第2阶段传输SNR分别表示为SNR1, m、SNR2, m:
式中:
式中: 1/2表示中继系统工作在半双工模式。在不完美的CSI下, 信道增益噪声比可以表示为式(8), 其中Ni(i=1, 2) 为中继节点和目的节点的噪声功率谱密度, B为系统总带宽, η是SNR差额, 当系统处于正交振幅调制(quadrature amplitude modulation, QAM), 取值η=-ln 5BER/1.5。
2.2 条件概率建模
本文从不完美的CSI出发, 考虑CSI在实际的水声信道中通常是过时的, 使用条件概率用已知的CSI推导出理论完美的CSI, 并进行遍历容量最大建模, 借助改进的自适应功率分配算法, 可基于不完美CSI实现较为理想的资源分配。该方案在保证性能的前提下降低了对CSI完美程度的要求, 复杂度更低, 开销更少。时变多途水声信道的时域表达式如下:
式中: h(τ, t)信道共P条路径, 第p条路径复增益为Ap(t), 时延为τp(t)。
考虑3种导致瞬时CSI不完美的因素, 包括信道估计误差和反馈延迟, 真实的信道增益表达式都可以表示为
式中: g是上述2种因素影响下直接得到的信道增益;
对于给定的
式中:
2.3 遍历容量最大化建模
将接收端返回到发射端的g[m]为作
式中: pi, m(i=1, 2, 3)是在不同的自适应资源分配系统中第m个子载波对应的发射功率。在总发射功率的约束条件下, 系统的遍历容量最大化准则可以表述为
式中: PT是发射端可利用的最大功率; Sp是数据子载波集。对于给定子载波的分配, 原始问题可以写成如下形式:
该问题是一个凸优化问题, 可以用凸优化的解决方法获得最优解。注水分配算法作为大部分自适应算法的理论基础, 在理论上是功率分配的最优算法。为求最优解, 可以构造如下拉格朗日方程:
根据对偶优化理论, 寻求最优的pk, 使得L值最大, 将L对pm求偏导:
该导数随着pm的增大而减小, 因此当导数等于0时, L取得最大值。经计算得
式中: pm*为最优分配功率, 又由于式(18)的左边是一个单调递减函数, 因此最多只有一个解, 即:
式中: 遍历速率为
3 实验与性能分析
本文利用Matlab软件对所提方案进行仿真实验, 仿真平台为Windows11 AMD Ryzen 7 4700U。本文采用随机中继的方式, 假设源节点-中继节点-目的节点之间的距离为1.5 km。本文对10 000 m(长)×10 000 m(宽)×5 000 m(深) 的仿真场景划分为4层结构, 并在其中部署50个异构节点。其中, 在海底层部署20个收集数据的终端感知节点, 其他3层部署10个节点, 承担数据收集的任务并将来自底层的数据上传到汇聚节点。
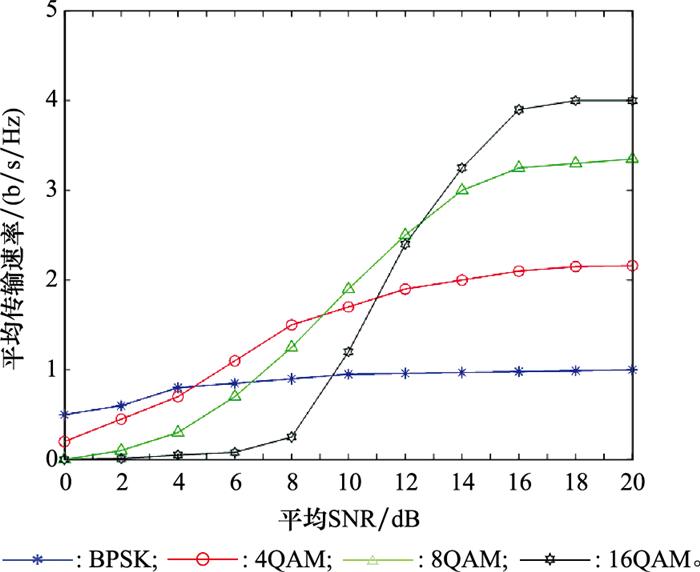
水声信道面临带宽资源有限的问题, 在一定的发射功率限制下, 为了实现发射端和接收端之间的信道容量最大化, 可使用注水算法对子载波进行功率分配。现有一些理论研究通常将各个子信道视作等增益的, 但实际中由于频率选择性衰落各个子信道上的衰落情况是不同的, 因此如果统一调制则会出现频带浪费或误码率过高的情况, 在满足系统通信速率的要求下, 应该基于反馈的信道情况和通信质量的要求进行自适应调制。OFDM中通常可选择的调制方式有BPSK、4QAM、8QAM、16QAM这4种。4种调制方式在平均传输速率上的性能如图 5所示。
图5
图5
不同调制方式的平均传输速率比较
Fig.5
Average transmission rate comparison of different modulation
表1 调制切换阈值
Table 1
| 模式 | 调制方式 | 阈值区间/dB |
| 1 | BPSK | SNR≤5 |
| 2 | 4QAM | 5<SNR≤9 |
| 3 | 8QAM | 9<SNR≤14 |
| 4 | 16QAM | 14<SNR |
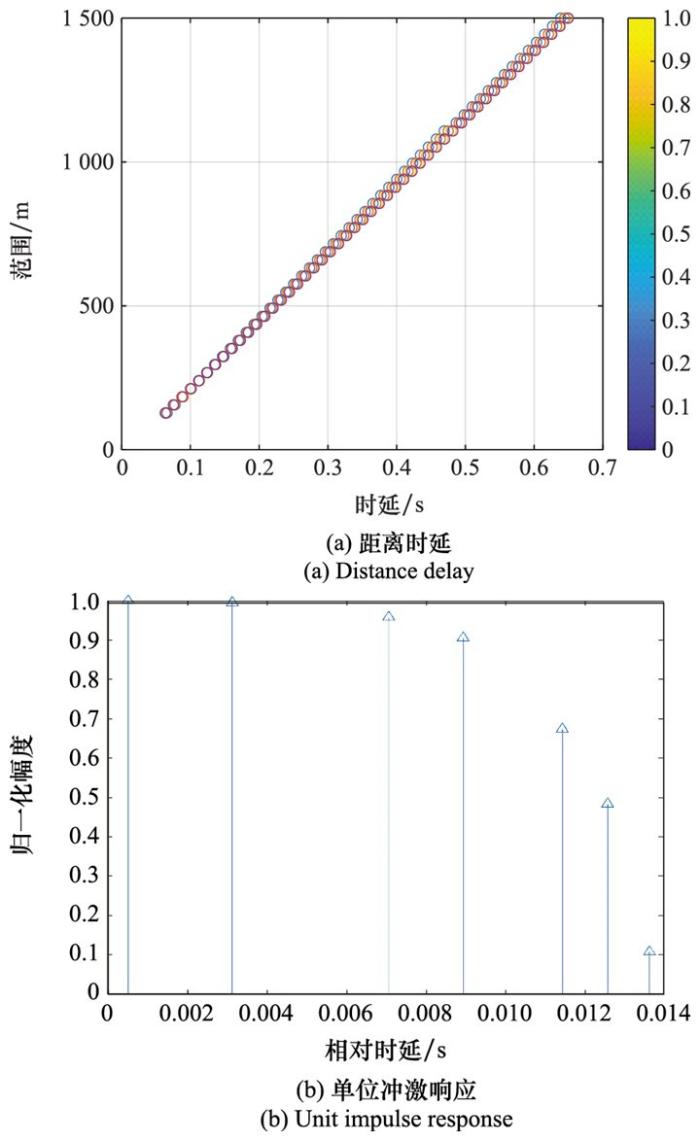
本文采用考虑多种变化因素的水声建模方法, 利用Bellhop射线声学模型计算本征路径, 并在此基础上模拟多种因素引起的小尺度衰落, 仿真参数如表 2所示。
表2 实验参数设置
Table 2
| 实验参数 | 取值 |
| 水深/m | 5 000 |
| 通信半径/m | 2 000 |
| 声速/(m/s) | 1 500 |
| 海面波动幅度/m | ±1 |
| 通信距离变化/m | ±2 |
| 子载波总数量 | 64 |
| 水下节点数量 | 50 |
| 带宽/kHz | 6(21~27) |
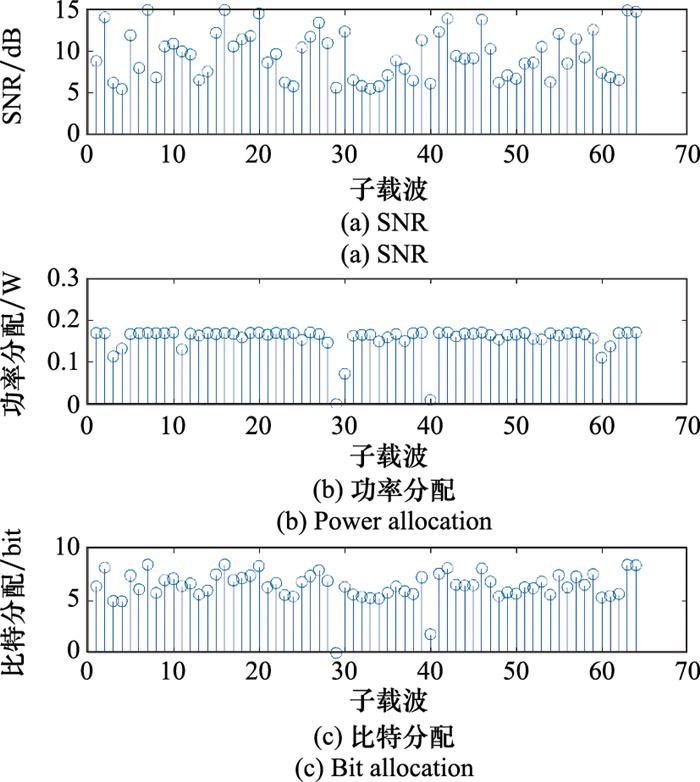
图6
图7
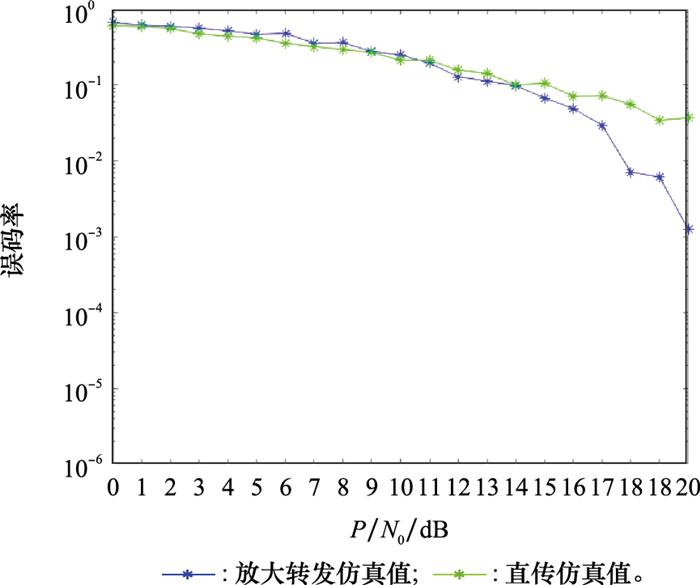
直传非中继系统与放大转发系统仿真关于误码率性能的比较如图 8所示。由于本文采用随机中继的方式, 中继系统在中继节点的选择策略上具有更多随机性, SNR较低时, 容易受到噪声干扰。随着SNR的增加, 相比直传系统, 中继系统的优势更加明显。可以看出,两种方式随着SNR的增加, 两种方式的误码率性能都得到提升。在高SNR的情况下, 协作中继方法转发对于误码率的改善更为明显。在SNR为20 dB时, AF方式可以比直传时获得大概两个百分点的的误码率增益, 这说明中继放大转发协作OFDM通信系统可以获得分集增益, 显著降低系统误码率, 提高系统可靠性。
图8
图8
AF与直传方式误码率性能的比较结果
Fig.8
Comparison result of bit error rate performance between AF and direct transmission
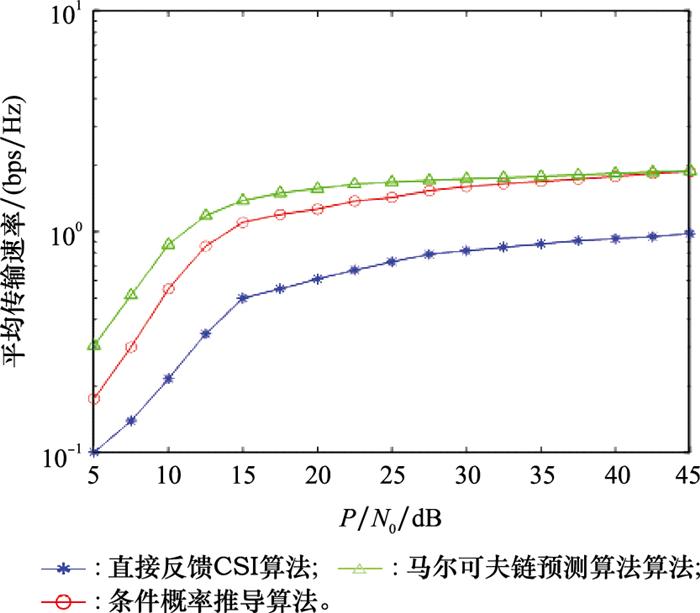
本文算法与文献[30]提出的基于马尔可夫链预测CSI的方法, 以及直接反馈过时CSI进行资源分配的算法关于平均传输速率性能的比较如图 9所示。可以看出, 3种算法随着SNR的增加平均传输速率都在不同程度的增加。特别当SNR小于15 dB时, 基于马尔可夫预测的算法平均传输速率性能优于基于条件概率的算法, 直接反馈CSI的算法的性能表现最差。但当SNR>25 dB时, 基于预测的算法和条件概率推到算法的平均传输速率表现逐渐趋于一致, 直接反馈CSI的算法平均传输速率也得到有效提升, 这是因为当信道状态良好的时候, 反馈的CSI也会趋于稳定, 此时自适应算法的系统平均传输速率性能表现最好。由于基于马尔可夫链预测的算法充分利用感知到的时延CSI和信道统计量来预测数据传输时的CSI, 并由此确定最佳比特负载和功率分配, 因此平均传输速率性能优于本文提出的条件概率推导CSI算法, 但是预测算法关于状态变化概率和矩阵运算的复杂度高于本文提出的算法, 本文基于此对两种算法进行了算法复杂度的比较。
图9
图9
平均传输速率性能的比较结果
Fig.9
Comparison results of average transmission rate performance
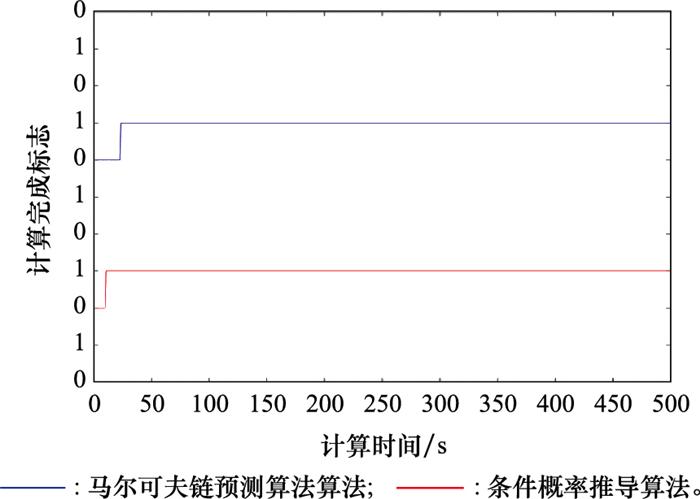
基于马尔可夫链的算法与本文提出的算法关于算法复杂度的比较如图 10所示。本文通过0-1表示算法完成与否, 0表示算法还未完成计算, 1表示算法已经成功计算。可以看出,本文提出的算法在10 s左右已经完成了计算, 而基于预测的算法完成时间远长于本文提出的算法, 大约在23 s才完成了自适应资源分配算法的整体计算。因此, 虽然预测算法的平均传输速率在低SNR的情况下优于本文提出的算法, 但是均衡算法复杂度, 本文提出的算法耗费更少的计算资源, 更适合高SNR的场景。
图10
4 结论
本文针对水声信道信道时变、带宽资源有限、环境复杂因素对自适应资源分配性能的影响, 构建中继放大协作OFDM通信系统模型, 提出利用条件概率对不完美的CSI推导出数据传输时的CSI, 并进行自适应资源分配, 克服了水声信道中具有大时延反馈的CSI不准确问题。仿真结果表明, 本文所构建的中继放大系统优于直传系统的误码率性能, 所提出的条件概率表征不完美CSI的算法平均传输速率性能优于直接反馈CSI的算法, 在高SNR的情况下与基于马尔可夫链预测的算法性能基本一致, 虽然低SNR时平均传输速率次于基于预测的方法, 但通过比较两种方法的算法度, 本文提出的算法相比基于马尔可夫链预测的算法更简单, 更加适用于能量有限的水声系统。
参考文献
基于马尔可夫状态空间的水声正交频分复用技术资源分配
[J].
Resource allocation of underwater acoustic orthogonal frequency division multiplexing based on Markov state space
[J].
水声通信网络信道建模与仿真研究进展
[J].DOI:10.3969/j.issn.1671-1815.2021.04.002 [本文引用: 1]
Progress in channel modeling and simulation of underwater acoustic communication network
[J].DOI:10.3969/j.issn.1671-1815.2021.04.002 [本文引用: 1]
The effect of directional ambient noise on an underwater acoustic link in shallow environments
[J].DOI:10.1109/JOE.2022.3178816 [本文引用: 1]
海洋生态文明建设背景下的海洋资源经济与海洋战略
[J].
Marine resource economy and marine strategy under the background of marine ecological civilization construction
[J].
A survey on underwater wireless sensor networks: requirements, taxonomy, recent advances, and open research challenges
[J].DOI:10.3390/s20185393 [本文引用: 1]
Transmission of information in a terminal discrete memoryless channel
[J].
Capacity theorems for the relay channels
[J].DOI:10.1109/TIT.1979.1056084 [本文引用: 1]
Efficient estimation and prediction for sparse time-varying underwater acoustic channels
[J].DOI:10.1109/JOE.2019.2911446 [本文引用: 1]
Real signal DHT-OFDM with index modulation for underwater acoustic communication
[J].
Joint CFO, gridless channel estimation and data detection for underwater acoustic OFDM systems
[J].
Adaptive modulation and coding for underwater acoustic OFDM
[J].DOI:10.1109/JOE.2014.2323365 [本文引用: 1]
Adaptive OFDMA with partial CSI for downlink underwater acoustic communications
[J].DOI:10.1109/JCN.2016.000054 [本文引用: 1]
Channel state information-based ranging for underwater acoustic sensor networks
[J].DOI:10.1109/TWC.2020.3032589 [本文引用: 1]
Adaptive coding and bit-power loading algorithms for underwater acoustic transmissions
[J].DOI:10.1109/TWC.2021.3070363 [本文引用: 1]
Channel state information prediction for adaptive underwater acoustic downlink OFDMA system: deep neural networks based approach
[J].DOI:10.1109/TVT.2021.3099797 [本文引用: 1]
Self-adaptive resource allocation in underwater acoustic interference channel: a reinforcement learning approach
[J].DOI:10.1109/JIOT.2019.2962915 [本文引用: 1]
Fundamentals of acute relay CSI severity
[J].
基于BELLHOP的水声信道时变模型
[J].
Time-varying model of underwater acoustic channel based on BELLHOP
[J].
Optimal resource allocation in the OFDMA downlink with imperfect channel knowledge
[J].DOI:10.1109/TCOMM.2009.0901.060546 [本文引用: 1]