近年来, 先进体制雷达逐步向智能化方向发展, 其反对抗能力得到了极大提升, 促使雷达对抗方开始研究构建包括态势感知、干扰效果评估、自适应干扰在内的闭环认知对抗系统^[1]。干扰效果评估是认知对抗系统实现闭环的关键环节, 只有准确地评估, 才能及时准确地反馈干扰实施的效果, 从而进行干扰策略和参数的优化调整^[2]。因此, 非合作条件下的干扰效果评估及干扰参数优化已经成为雷达对抗研究领域的一个热点问题。

干扰效果评估是指在对雷达实施干扰后定性或定量评价雷达受到的损伤或破坏的过程。传统的干扰效果评估多为合作式评估, 需要雷达方提供一定实验数据, 以雷达对应系统功能或性能作为评估指标, 依照一定评估准则对评估指标在受干扰前后的数值进行数学计算和分析来实现。评估常用的效能评估准则包括功率准则、信息准则、效率准则、时间准则等, 具体的评估计算方法主要包括评估因子法、模糊综合评估法和智能评估法等。不同评估指标和方法在具体应用中可以组合使用, 如文献[3-4]均在采用智能评估法的同时充分发挥了评估因子法、模糊综合评估法的优势。

在真实对抗作战场景中, 对抗方只能根据己方可以侦察感知到的雷达发射信号、波束转换、平台机动等多方面因素进行干扰评估, 因此需要研究非合作条件下的干扰效果评估方法。文献[5]提出了非合作式干扰效果评估的必要性、判定标准和具体方法, 通过对比在干扰实施前后侦察接收到的雷达发射信号变化, 结合先验知识进行间接评估。Ou等根据干扰前后截获的雷达信号的脉冲幅度和数据率的变化, 以截获信号的幅度累积量作为特征统计量, 设计了基于显著性检验的自屏蔽干扰效能评估检测器^[6]。文献[5-7] 中具体的评估计算过程, 均是根据侦察到的雷达发射信号的变化情况分析得出雷达参数、状态、模式等不同层次的评估指标, 经过综合计算间接评判干扰效果。上述研究所给评估方法的指标计算过程十分依赖专家经验和战前情报, 且侦收的雷达发射信号几乎是唯一的评估信息源, 携带反映雷达系统内部真实状态的信息量有限。因此，研究能够定量感知雷达系统内部各环节的状态在干扰前后变化情况, 实现高可信信息支撑的非合作在线干扰效果评估方法非常必要。

逆处理是通过研究系统外部行为或表现逆向推理系统内部细节的方法。Kalman早在1964年发表的文献[8]中就研究了逆最优控制问题, 目的是确定给定控制策略的成本准则是最优的。近年来逆处理问题在多个领域引起了关注。在人工智能领域, 逆强化学习是典型的逆处理问题, 即在给定策略或观测行为的条件下逆向推断智能体的奖励函数^[9-17]。在电子对抗领域, Krishnamurthy在文献[14]中以具有波形优化能力的认知雷达为对抗对象, 首次提出利用微观经济学中的显示偏好理论检验雷达是否具有认知能力, 并在具有认知能力的情况下估计雷达方波形优化的效用函数。文献[15]基于上述逆强化学习方法提出了对抗自适应雷达系统的处理框架, 提出利用逆滤波处理可以估计雷达方的最优估计和传感器精度以实现逆跟踪。

经典的逆滤波问题主要讨论的是如何通过贝叶斯滤波输出的状态后验估计滤波输入或传感器精度^[16]。从1979年开始, 就已经有专家学者对线性高斯状态空间模型下的Kalman滤波的逆滤波问题进行了研究^[17-19]。文献[16] 针对线性高斯状态空间模型下的两类问题进行了探讨, 针对已知状态后验为真实后验和状态后验带有噪声的两种情况分别提出了对应的逆滤波算法。文献[20]讨论了离散的隐马尔可夫模型(hidden Markov models, HMM) 下的逆滤波问题, 提出了基于聚类算法的逆HMM滤波算法。文献[21]中讨论了逆HMM滤波在电子对抗领域的应用, 通过逆滤波估计所对抗的目标雷达滤波输出及其后验分布和传感器精度, 可为对抗系统自适应干扰提供参考基础。文献[22] 研究了针对Kalman滤波、粒子滤波^[23]等逆滤波处理在对抗自适应雷达系统方面的应用。上述研究均说明, 通过逆滤波处理可以获取雷达滤波输出及其状态后验估计, 为非合作对抗系统实现相应的干扰效果评估提供了新的途径。

本文基于针对雷达系统进行逆处理的思路, 设计了一种基于逆滤波处理估计雷达跟踪误差, 进而实现非合作干扰效果在线评估的方法。以对抗方针对导引头雷达实施距离门拖引干扰(range gate pull off, RGPO)进行自卫为例, 仿真验证了所提方法的可行性和有效性。

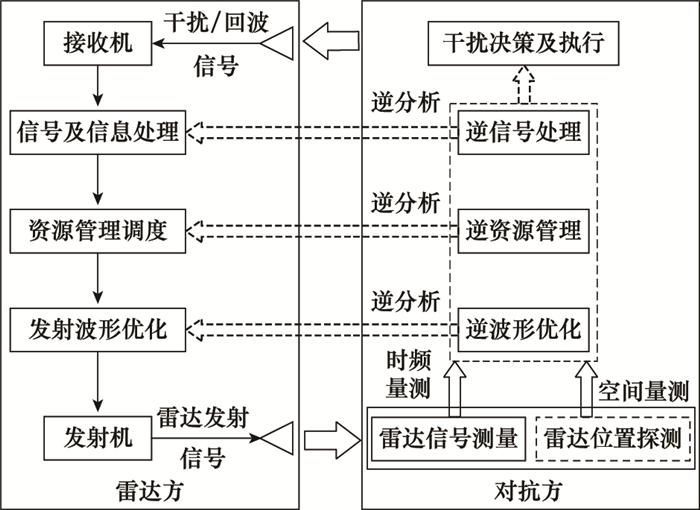
如图 1所示, 雷达系统可由信号收发、信号及信息处理、资源调度、波形优化模块组成。信号收发模块经过天线实现雷达发射信号和回波信号的发射和接收, 信号处理部分实现如脉冲压缩、恒虚警率(constant false alarm rate, CFAR)检测及目标跟踪滤波等处理, 资源调度和波形优化可通过如强化学习等方法实现雷达系统自适应资源调度和认知波形优化。

对抗方对雷达方进行逆分析处理时, 可根据分析对象在雷达系统中所处位置, 模块化映射为慢时间域的逆波形优化和逆资源管理、快时间域的逆信号处理等3个功能模块。逆波形优化模块可以基于接收雷达信号序列的参数测量结果, 对雷达方的发射信号波形优化目标函数进行反演分析, 支持干扰效果评估和干扰策略优化, 具体可利用逆强化学习的方法实现; 逆资源管理模块可基于雷达方系统行为序列观测结果, 对雷达方的资源管理调度目标函数进行反演分析, 支持干扰策略优化, 资源管理逆分析也可通过逆强化学习方法实现; 逆信号处理模块可以基于接收雷达信号变化或者雷达平台机动变化, 即时对雷达方信号或信息处理对应关键节点状态进行推理, 如本文研究的根据雷达平台空间量测逆滤波处理实现雷达目标跟踪中的跟踪误差估计, 进而实现干扰效果评估和干扰策略优化。其中, 雷达平台空间量测可由载机自身搭载的有源探测系统或外部辅助探测系统、或通过侦干探通一体化技术支持得到^[24-25]。

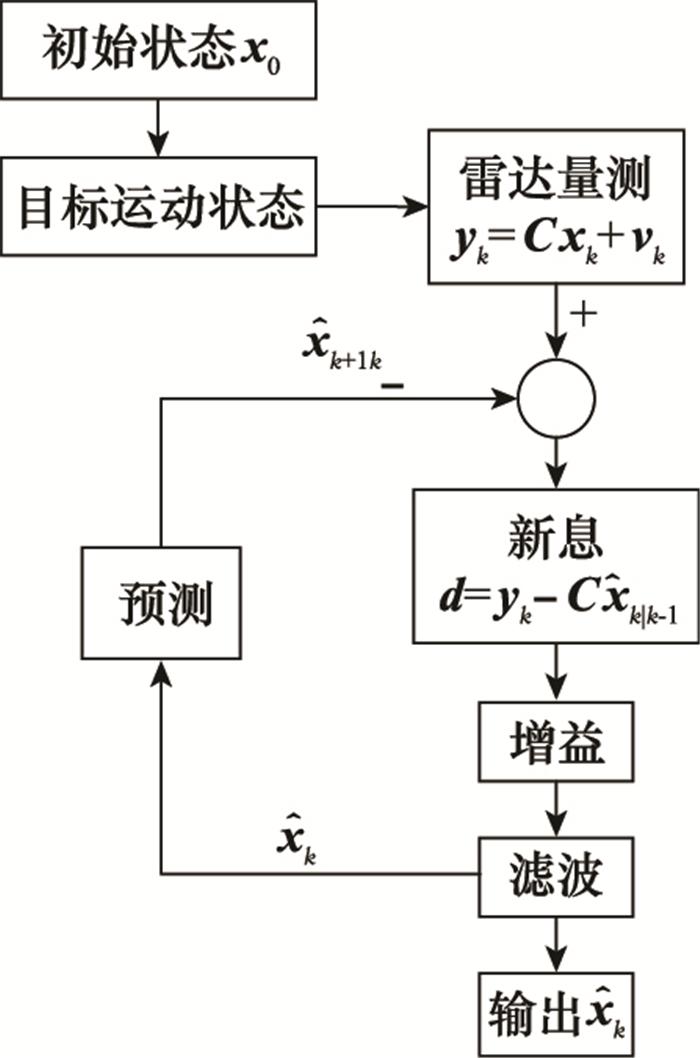
本文拟用的逆滤波处理属于上述框架中的逆信号处理层, 可以实现对雷达跟踪误差的估计。雷达实现目标状态稳定跟踪的基本原理如图 2所示, 其中目标运动状态向量用x_k表示, y_k为雷达对目标运动状态的带噪量测, 新息向量d由雷达量测y_k和状态预测量x_k|k－1计算得到, 然后按照一定准则或方法调整滤波增益与协方差矩阵, 最后得出目标状态估计${{{\boldsymbol{\hat x}}_{k}}}$和下一时刻目标状态的预测值x_k+1|k并参与下一时刻滤波。

具体来说, 雷达滤波过程如下所示:

(1) ${\boldsymbol{x}}_k \sim P_{x_{k-1}, x}=p\left({\boldsymbol{x}} \mid {\boldsymbol{x}}_{k-1}\right), {\boldsymbol{x}}_0 \sim \pi_0$

(2) ${\boldsymbol{y}}_k \sim B_{{\boldsymbol{x}}_{k}, {\boldsymbol{y}}}=p\left({\boldsymbol{y}} \mid {\boldsymbol{x}}_k\right)$

(3) $\pi_k=T\left(\pi_{k-1}, {\boldsymbol{y}}_k\right)=p\left({\boldsymbol{x}}_k \mid {\boldsymbol{y}}_{1: k}\right)$

式中: k=1, 2, …, N表示离散化时间; p(·)表示条件概率密度函数; x_k是基于马尔可夫过程的目标真实运动状态; P_{xk-1, x}表示状态转移规则; π₀表示目标初始状态分布; y_k表示雷达方对目标运动状态的带噪观测值, 服从观测偏好B_{xk, y}; 式(3)表示雷达对目标运动状态x_k的状态后验估计, 将雷达滤波后的输出记为${{{\boldsymbol{\hat x}}_{k}}}$。T算子代表不同的滤波器, π_k为雷达估计得到的目标状态后验分布。

逆滤波处理的输入为对抗方对雷达方根据滤波结果${{{\boldsymbol{\hat x}}_{k}}}$及π_k所采取的后续系统动作的带噪观测。后续系统动作可以是平台运动、波形选择、资源管理等, 记为u_k, 雷达动作的带噪观测记为a_k, 则有

(4) ${\boldsymbol{a}}_k \sim G_{\hat{{\boldsymbol{x}}}_k, \pi_k, a}=p\left(a \mid \hat{{\boldsymbol{x}}}_k, \pi_k\right)$

式中: ${G_{{{\boldsymbol{\hat x}}_k}, {\pi _k}, a}}$是在给定${{{\boldsymbol{\hat x}}_{k}}}$, π_k的情况下观察雷达方行动a_k的条件概率。

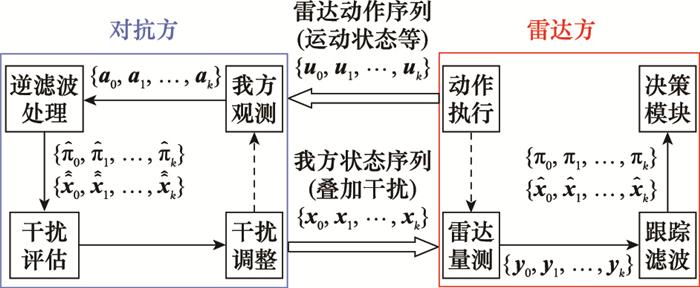
基于式(1)~式(4)建立对抗模型如图 3所示, 图中雷达方系统功能映射为量测模块、跟踪模块、决策模块、执行模块, 与对抗方交互量为叠加干扰的目标运动状态x_k和雷达动作状态u_k^[14]。由此, 针对雷达跟踪模块的逆滤波处理问题可以表述为: 根据已知的目标自身运动状态序列x_0:k和雷达方动作的带噪量测序列a_1:k估计雷达对目标运动状态的估计${{{\boldsymbol{\hat x}}_{k}}}$或其后验分布π_k。当雷达方采用Kalman滤波算法或基于Kalman滤波的概率数据关联(probabilistic data association, PDA)算法时, π_k为高斯分布N(${{{\boldsymbol{\hat x}}_{k}}}$, Σ_k), 其中Σ_k为状态估计${{{\boldsymbol{\hat x}}_{k}}}$的协方差, 因此两者可互相转换。

具体来说, 假设已知概率分布P_{xk-1, x}、B_{xk, y}、${G_{{{\boldsymbol{\hat x}}_k}, {{\rm{ \mathsf{ π} }}_k}, \boldsymbol{a}}}$, 逆滤波处理可用下式表示:

(5) $\alpha_k\left(\hat{{\boldsymbol{x}}}_k\right)=p\left(\hat{{\boldsymbol{x}}}_k \mid \hat{{\boldsymbol{x}}}_0, {\boldsymbol{a}}_{1: k}, {\boldsymbol{x}}_{0: k}\right)$

逆滤波后可得对雷达估计${{{\boldsymbol{\hat x}}_{k}}}$的估计$\hat{\hat{\boldsymbol{x}}}_k$, 结合目标真实运动状态x_k, 即可估计雷达方跟踪误差为$\hat{\boldsymbol{e}}_k=\left|\hat{\hat{\boldsymbol{x}}}_k-\boldsymbol{x}_k\right|$。

针对距离假目标、速度假目标、距离拖引干扰、速度拖引干扰等旨在破坏雷达跟踪精度的干扰样式, 可以利用对雷达跟踪误差的估计实现非合作条件下的干扰效果在线评估。

针对噪声、杂波环境、多目标、目标机动等不同应用场景, 研究者针对性地提出了许多雷达跟踪滤波算法。不同雷达滤波算法需要推导与其匹配的逆滤波处理算法, 文献[14-16] 在给出逆滤波处理概念时, 已针对基本Kalman滤波算法的逆滤波过程进行了讨论。考虑末制导雷达导引头在实际拦截攻击机动目标时会遇到有杂波信号的场景, 本文针对可以适用杂波背景的PDA滤波算法, 推导了对应的逆滤波处理方法。

PDA滤波算法是标准Kalman滤波结合概率数据关联思想的一种跟踪滤波算法, 能够很好地解决杂波场景下的目标跟踪问题^[26]。

PDA滤波的目标状态模型为

(6) ${\boldsymbol{x}}_{k+1}={\boldsymbol{A}} {\boldsymbol{x}}_k+{\boldsymbol{w}}_k, {\boldsymbol{x}}_0 \sim \pi_0$

式中: A为状态转移矩阵; w_k为服从高斯分布的状态过程噪声, w_k~N(0, Q_k); Q_k为过程噪声协方差; π₀~N($\hat{\boldsymbol{x}}_0$, Σ₀), Σ₀为初始滤波协方差。

杂波背景下k时刻落入相关波门内的量测不止一个, 记y_kⁱ(i=1, 2, …, m_k)为k时刻波门内的第i个量测, m_k为落入波门内的有效量测数目, 当该量测源于真实目标时有

(7) ${\boldsymbol{y}}_k^i={\boldsymbol{C}} {\boldsymbol{x}}_k+{\boldsymbol{v}}_k$

式中: C为量测矩阵; v_k~N(0, R_k)为量测噪声; R_k为量测噪声协方差矩阵。

在杂波背景下, 雷达方利用量测值计算$\hat{\boldsymbol{x}}_k$和π_k~N($\hat{\boldsymbol{x}}_k$, Σ_k), 该过程分为状态预测、关联概率计算和状态更新3步。最终得出对目标状态的估计为

(8) $\hat{{\boldsymbol{x}}}_k={\boldsymbol{A}} \hat{{\boldsymbol{x}}}_{k-1}+{\boldsymbol{K}}_k \sum\limits_{i=1}^{m_k} \beta_k^i\left({\boldsymbol{y}}_k^i-{\boldsymbol{C A}} \hat{{\boldsymbol{x}}}_{k-1}\right)$

滤波误差协方差如下:

(9) $\begin{gathered}{\boldsymbol{\varSigma}}_k=\beta_k^0 {\boldsymbol{\varSigma}}_{k \mid k-1}+\left(1-\beta_k^0\right)\left[{\boldsymbol{\varSigma}}_{k \mid k-1}-{\boldsymbol{K}}_k {\boldsymbol{S}}_k {\boldsymbol{K}}_k^{{\mathrm{T}}}\right]+ \\{\boldsymbol{K}}_k\left[\sum\limits_{i=1}^{m_k} \beta_k^i {\boldsymbol{s}}_k^i {\boldsymbol{s}}_k^{i {\mathrm{~T}}}-{\boldsymbol{s}}_k {\boldsymbol{s}}_k^{{\mathrm{T}}}\right] {\boldsymbol{K}}_k^{{\mathrm{T}}}\end{gathered}$

式中: β_kⁱ(i=0, 1, 2…, m_k)为每个候选量测的关联概率; s_k为组合新息^[27]; K_k表示滤波增益; Σ_k|k－1是根据前一时刻滤波协方差预测的误差协方差。

上述过程涉及两个随机事件θ_kⁱ$\triangleq${y_kⁱ来自目标的量测}, θ_k⁰$\triangleq${k时刻相关波门内无来自目标的量测}, 记k时刻的量测来自于目标的条件概率为β_kⁱ, k时刻的量测不是源自目标的条件概率为β_k⁰, 则

(10) $\sum\limits_{i=0}^{m_k} \beta_k^i=1$

雷达可根据上述滤波结果和某些预制函数选择其动作为u_k^[22]。若雷达方为雷达导引头, 该动作可以是基于线性二次型高斯(linear quadratic Gaussian, LQG)理论设计的最优制导律, 即雷达导引头的加速度状态。若雷达方为认知雷达, 则该动作可以为雷达波形设计或资源管理动作, 即雷达系统的发射波形或资源分配结果。对抗方在噪声中观测到的雷达方动作a_k如下:

(11) ${\boldsymbol{a}}_k={\boldsymbol{u}}_k+{\boldsymbol{\mu}}_k=\overline{{\boldsymbol{C}}}_k \hat{{\boldsymbol{x}}}_k+{\boldsymbol{\mu}}_k$

式中: μ_k为服从高斯分布的量测噪声, μ_k~i.i.d N(0, σ_μ²); σ_μ²为量测噪声协方差; C_k为动作矩阵。

将式(7)代入式(8)可得

(12) $\hat{{\boldsymbol{x}}}_k=\left({\boldsymbol{I}}-{\boldsymbol{K}}_k {\boldsymbol{C}} \sum\limits_{i=1}^{m_k} \beta_k^i\right) {\boldsymbol{A}} \hat{{\boldsymbol{x}}}_{k-1}+\sum\limits_{i=1}^{m_k} \beta_k^i {\boldsymbol{C}} {\boldsymbol{K}}_k {\boldsymbol{x}}_k+\sum\limits_{i=1}^{m_k} \beta_k^i {\boldsymbol{K}}_k {\boldsymbol{v}}_k$

由式(10)可得

(13) $\sum\limits_{i=1}^{m_k} \beta_k^i=1-\beta_k^0$

由于β_k⁰的计算依赖于雷达方的真实观测集, 而对抗方无法获取该观测集, 本文采取与文献[27]中类似的处理方法, 以β⁰代替β_k⁰, 即

(14) $\bar{\beta}^0={\mathrm{E}}\left[\beta_k^0 \mid Y^k\right]=p\left(\theta_k^0 \mid Y^k\right)=1-P_D P_G$

式中: P_D为检测概率; P_G是n维量测落入波门内的概率; 与雷达方相同, P_D和P_G根据专家经验得出^[27]。将式(14)代入式(12)可得对抗方逆PDA滤波模型的状态方程为

(15) $\hat{{\boldsymbol{x}}}_k=\left({\boldsymbol{I}}-{\boldsymbol{K}}_k {\boldsymbol{C}} {\boldsymbol{P}}_D P_G\right) {\boldsymbol{A}} \hat{{\boldsymbol{x}}}_{k-1}+P_D P_G {\boldsymbol{C}} {\boldsymbol{K}}_k {\boldsymbol{x}}_k+P_D P_G {\boldsymbol{K}}_k {\boldsymbol{v}}_k$

由状态方程式(15)和量测方程式(11)可知, 逆PDA滤波模型是一个线性高斯模型, 可采取与标准Kalman滤波类似的方法进行逆处理。为了便于描述, 将对抗方逆滤波使用的状态矩阵、控制矩阵、状态过程噪声、量测噪声如下所示:

(16) $\left\{\begin{array}{l}\overline{{\boldsymbol{A}}}_k=\left({\boldsymbol{I}}-P_D P_G {\boldsymbol{K}}_{k+1} {\boldsymbol{C}}\right) {\boldsymbol{A}} \\\overline{{\boldsymbol{F}}}_k=P_D P_G {\boldsymbol{K}}_{k+1} {\boldsymbol{C}} \\\overline{{\boldsymbol{Q}}}_k=P_D P_G {\boldsymbol{K}}_k {\boldsymbol{K}}_k^{{\mathrm{T}}} \\\overline{{\boldsymbol{R}}}={\boldsymbol{\sigma}}_\mu^2\end{array}\right.$

在概率分布P_{xk-1, x}、B_{xk, y}、$G_{{\boldsymbol{\hat{x} }}_k, \pi_k, {\boldsymbol{ a}}}$已知的条件下, 式(16) 中除K_k+1外的其他参数均已知。根据PDA滤波算法可知计算K_k+1需已知前一时刻的雷达滤波的滤波误差协方差Σ_k。而Σ_k需知雷达真实量测, 因此无法直接模拟计算K_k+1, 需要雷达方的滤波协方差Σ_k进行估计。在无法获知雷达真实量测的情况下, 本文通过修正的Riccati方程^[28]估计滤波协方差:

(17) ${\boldsymbol{\varSigma}}_k={\boldsymbol{\varSigma}}_{k \mid k-1}-\frac{c P_D}{1+a P_D^{1-b} \lambda V_k} {\boldsymbol{K}}_k {\boldsymbol{S}}_k {\boldsymbol{K}}_k^{{\mathrm{T}}}$

式中: Σ_k|k－1= AΣ_k－1A^T+ Q_k; λ为杂波密度; a、b、c为3个计算因子, 可根据文献[28]查表得出。则

(18) ${\boldsymbol{K}}_{k+1}={\boldsymbol{\varSigma}}_{k+1 \mid k} {\boldsymbol{C}}^{{\mathrm{T}}} {\boldsymbol{S}}_{k+1}^{-1}=\left({\boldsymbol{A}} {\boldsymbol{\varSigma}}_k {\boldsymbol{A}}^{{\mathrm{T}}}+{\boldsymbol{Q}}\right) {\boldsymbol{C}}^{{\mathrm{T}}}\left({\boldsymbol{C}}\left({\boldsymbol{A}} {\boldsymbol{\varSigma}}_k {\boldsymbol{A}}^{{\mathrm{T}}}+{\boldsymbol{Q}}\right) {\boldsymbol{C}}^{{\mathrm{T}}}+{\boldsymbol{R}}\right)^{-1}$

根据上述推导, 对抗方实现逆PDA滤波的输入为雷达动作的带噪量测, 输出是雷达方对对抗方运动状态的估计的最优估计, 处理流程如图 4所示。

与图 4对应的具体逆滤波实现步骤如下。

步骤  1   对k=0时刻逆滤波最优估计$\hat{\hat{\boldsymbol{x}}}_0$、雷达滤波协方差Σ₀、逆滤波协方差Σ₀及逆滤波观测噪声协方差σ_μ²进行初始化。

步骤  2   当k≥1时, 根据式(18)计算雷达滤波增益K_k, 并根据式(16)计算逆滤波参数A_k－1、F_k－1、Q_k、R。

步骤  3   状态预测。

预测雷达对目标状态的最优估计:

(19) $\hat{\hat{{\boldsymbol{x}}}}_{k \mid k-1}=\overline{{\boldsymbol{A}}}_{k-1} \hat{\hat{{\boldsymbol{x}}}}_{k-1}+\overline{{\boldsymbol{F}}}_{k-1} {\boldsymbol{x}}_k$

预测对抗方逆滤波的误差协方差:

(20) $\overline{{\boldsymbol{\varSigma}}}_{k \mid k-1}=\overline{{\boldsymbol{A}}}_{k-1} \overline{{\boldsymbol{\varSigma}}}_{k-1} \overline{{\boldsymbol{A}}}_{k-1}^{{\mathrm{T}}}+\overline{{\boldsymbol{Q}}}_k$

步骤  4   状态更新。

对抗方逆PDA滤波增益为

(21) $\overline{{\boldsymbol{K}}}_k=\overline{{\boldsymbol{\varSigma}}}_{k \mid k-1} \overline{{\boldsymbol{C}}}_k^{{\mathrm{T}}}\left(\overline{{\boldsymbol{C}}}_k \overline{{\boldsymbol{\varSigma}}}_{k \mid k-1} \overline{{\boldsymbol{C}}}_k^{{\mathrm{T}}}+\overline{{\boldsymbol{R}}}\right)^{-1}$

利用k时刻对抗方对雷达方动作的噪声量测值a_k对步骤3所得预测状态值$\hat{\hat{\boldsymbol{x}}}_{k \mid k-1}$进行修正, 得到雷达方对对抗方状态估计的最优估计。这与雷达Kalman滤波中利用雷达目标运动状态的量测对其一步预测的目标运动状态进行修正类似:

(22) $\hat{\hat{{\boldsymbol{x}}}}_k=\hat{\hat{{\boldsymbol{x}}}}_{k \mid k-1}+\overline{{\boldsymbol{K}}}_k\left({\boldsymbol{a}}_k-\overline{{\boldsymbol{C}}}_k \hat{\hat{{\boldsymbol{x}}}}_{k \mid k-1}\right)$

更新k时刻的滤波协方差:

(23) $\overline{{\boldsymbol{\varSigma}}}_k=\left({\boldsymbol{I}}-\overline{{\boldsymbol{K}}}_k \overline{{\boldsymbol{C}}}_k\right) {\boldsymbol{\varSigma}}_{k \mid k-1}$

步骤  5   k=k+1, 跳转至步骤2进行下一时刻处理。

在二维平面内进行仿真, 雷达始终位于坐标原点, 在杂波背景下利用PDA滤波对目标的距离、速度信息进行滤波跟踪。目标初始位置为[5 km, 8 km], 并以100 m/s的速度沿x轴负方向做匀速直线运动, 仿真中时间间隔为Δt=1 s, 总时长为100 s。

雷达方滤波的目标模型为匀速(constant velocity, CV), 过程噪声均方差q为1, 量测噪声均方差r为10。对抗方利用逆Kalman滤波处理实现对雷达的逆跟踪, 动作矩阵C_k为

$\overline{{\boldsymbol{C}}}_k=\left[\begin{array}{llll}1 & 1 & 0 & 0 \\0 & 0 & 1 & 1\end{array}\right] \times {\boldsymbol{\varSigma}}_k$

假定雷达滤波检测概率P_D=1.0, 波门大小随滤波过程中的新息协方差变化, P_G=0.999 7。具体的杂波生成参考文献[29]中的方法, 杂波量测在关联波门内服从泊松分布。

对抗方在杂波下利用逆PDA滤波算法估计雷达对目标运动状态的估计, 进行100次蒙特卡罗实验, 通过计算均方根误差和均方根误差均值对逆PDA滤波算法估计雷达对目标运动状态估计的准确性进行评价。距离均方根误差(root mean square error, RMSE)及其均值计算公式如下:

(24) ${\mathrm{RMSE}}_{-} r(k)=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(\hat{\hat{r}}_k^{(i)}-\hat{r}_k^{(i)}\right)}$

(25) ${\text { AVRMSE }}\_{r}=\frac{1}{M} \sum\limits_{k=1}^M \sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(\hat{\hat{r}}_k^{(i)}-\hat{r}_k^{(i)}\right)}$

式中: N为蒙特卡罗实验次数; $\hat{\hat{r}}_k^{(i)}$、$\hat{r}_k^{(i)}$表示第i次实验k时刻的距离逆滤波值和滤波值。速度RMSE及其RMSE均值的计算方法类似。

(1) 不同对抗方量测噪声下的仿真实验

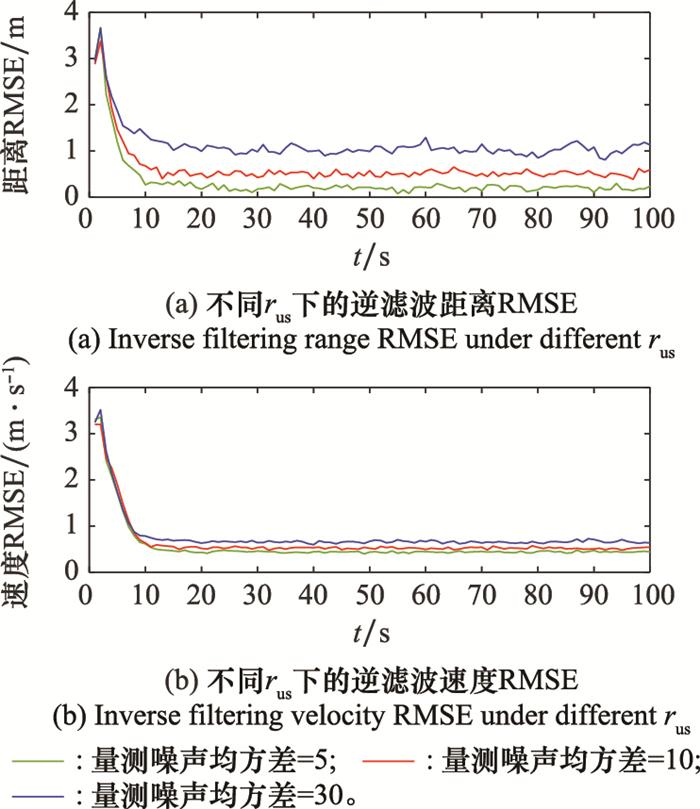
对抗方量测噪声均方差取r_us={5, 10, 30}, 仿真实验结果如图 5所示, 仿真中λ为0.000 1 s/m。

由图 5可知, 对抗方量测噪声均方差的大小会略微影响算法的收敛速度, 但在10帧后均收敛到稳定值, 说明杂波下逆PDA算法具有时效性。通过对比收敛后的RMSE可知, 当杂波密度固定时, 量测噪声均方差越大, 逆滤波估计的误差越大。

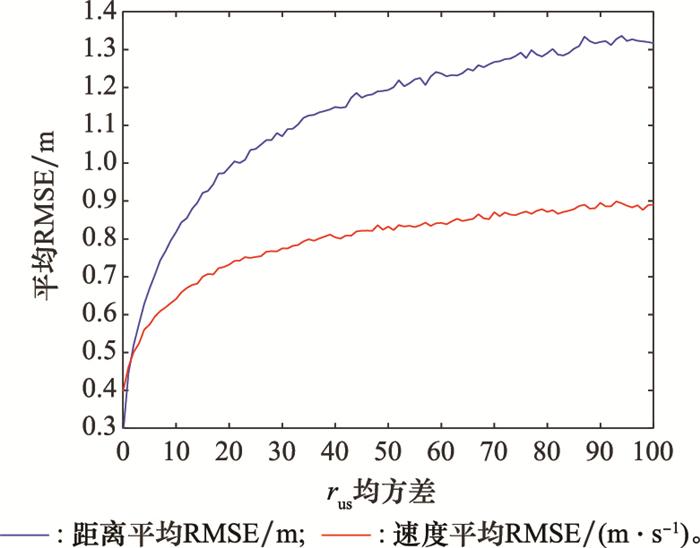
对抗方量测噪声均方差以1为步进遍历0~100区间, 所得平均RMSE如图 6所示。

由图 6可知, 当r_us为0时, 逆滤波AVRMSE最小, 随着r_us的增大, AVRMSE越来越大, 但当r_us增大到100时, 距离AVRMSE仍然较小, 小于1.5 m, 速度AVRMSE则始终小于1 m/s, 说明杂波下逆PDA滤波算法估计雷达最优估计的误差较小, 准确性高。

(2) 不同杂波密度下的仿真实验

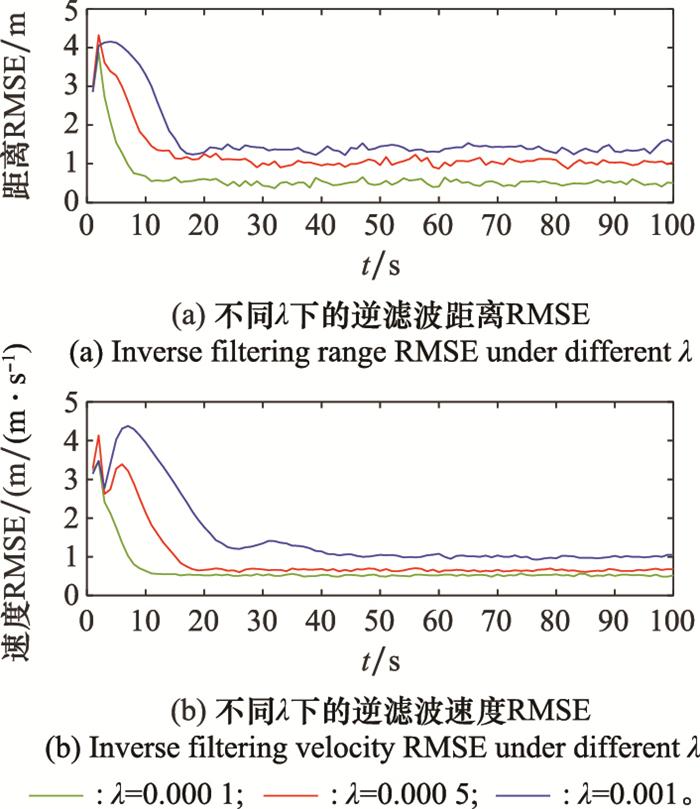
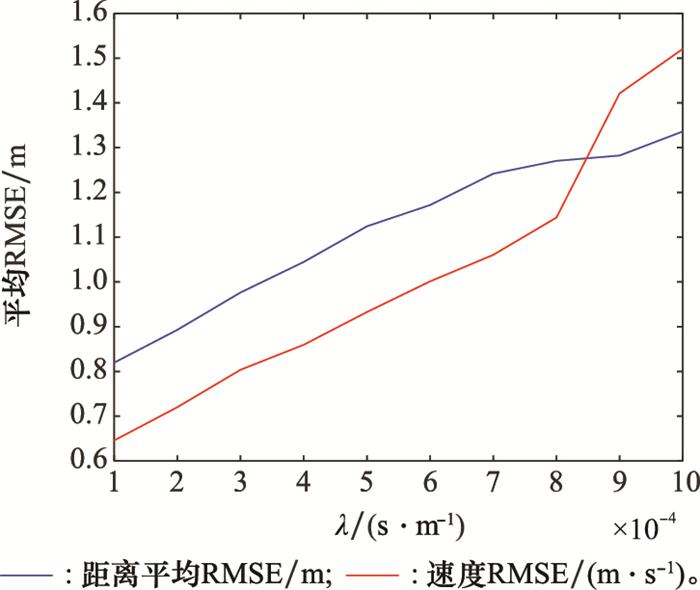
对抗方量测噪声均方差r_us=10, 杂波密度取λ={0.000 1, 0.000 5, 0.001}, 仿真所得逆滤波距离和速度RMSE如图 7所示。

由图 7可知, 杂波密度越大, 逆滤波算法的收敛速度越慢, 且逆滤波的估计误差越大。当杂波密度为0.000 1时, 算法收敛速度最快。当杂波密度为0.000 5时, 在15~20帧距离速度RMSE才收敛, 收敛后距离速度RMSE均大于λ=0.000 1时的实验结果。当杂波密度增大到0.001时, 算法的收敛速度最慢, 收敛后的RMSE最大。

图 8为以0.000 1为杂波密度步进值, 在不同杂波密度下实验所得AVRMSE结果。由图 8可知, 杂波密度越大, 距离和速度的平均RMSE值越大, 即逆滤波估计的误差越大。

综上所述, 杂波下逆滤波估计准确性与对抗方量测噪声和杂波密度有关, 量测噪声均方差和杂波密度越大, 逆滤波估计误差越大, 但当r_us和λ在正常范围内, 逆PDA滤波算法能够以较低误差估计雷达方对目标运动状态的估计, 因此可以利用对雷达最优估计的估计对雷达跟踪误差进行逆向计算, 为非合作条件下的干扰效果定量评估提供依据。

RGPO干扰是典型的可通过增大雷达跟踪误差, 逐渐引偏雷达致使雷达重新搜索的干扰样式, 本节以RGPO干扰为例, 设计通过逆滤波处理实现对抗方对雷达跟踪功能干扰效果的在线评估和干扰参数的实时优化。

RGPO干扰是最有效的欺骗干扰方法之一。典型的RGPO干扰的实施过程分为捕获期(停拖期)、拖引期、关闭期3个阶段^[30]。假设拖引期进行匀速拖引, 上述过程可用如下所示:

(26) $R_J(t)=\left\{\begin{array}{l}R+v_1 t, 0 \leqslant t<t_1 \\R+v_1 t+v_2\left(t-t_1\right), t_1 \leqslant t<t_2 \\{\text { 干扰关闭, }} t_2 \leqslant t<T_J\end{array}\right.$

式中: v₁为真实回波所代表的目标运动速度; v₂为对抗方拖引干扰的拖引速度; t₁为停拖期时长, t₂－t₁为拖引期时长; T_J为一个拖引周期。

RGPO干扰的效果与拖引策略有密切关系。若拖引速度太快则可能由于雷达方的距离跟踪系统难以及时响应, 导致干扰信号脱离雷达跟踪波门, 或被雷达抗干扰环节识别, 导致干扰失败, 若拖引速度太慢可能导致拖引期结束仍未将雷达跟踪波门拖离真实目标回波信号, 干扰也会失败。传统的RGPO干扰往往利用情报分析实现制定干扰策略, 在作战过程中按照固定策略实施干扰。且对干扰是否成功的判别, 也只能在一个干扰周期结束后通过状态识别判断雷达是否进入搜索状态来进行判定或根据多次试验数据计算拖引成功率进行干扰效果评估, 无法在一个干扰周期内对干扰效果进行在线评估, 并实时调整干扰策略参数^[30]。

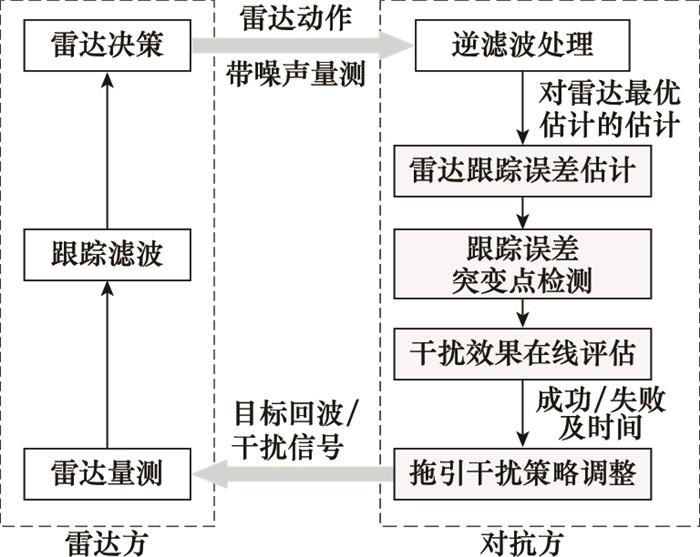
本节设计的基于逆滤波处理对RGPO干扰效果进行在线评估, 并根据评估结果动态调整干扰策略的方法总体流程如图 9所示。

(1) 雷达距离跟踪误差估计

以雷达动作在噪声中的量测a_k和自身运动状态x_k作为逆滤波处理的输入, 处理得到雷达对目标运动状态估计的估计值$\hat{\hat{\boldsymbol{x}}}_k$, 具体过程见第2节。则对抗方估计的雷达距离跟踪误差为$\hat{\boldsymbol{e}}_k=\left|\hat{\hat{r}}_k-r_k\right|$, 其中r_k为目标与雷达相对距离真实值, $\hat{\hat{r}}_k$为对抗方估计值。

(2) 距离跟踪误差突变点检测

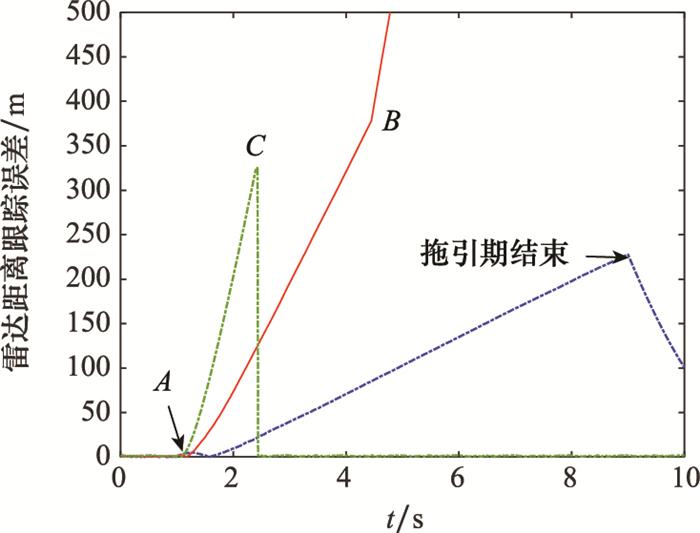
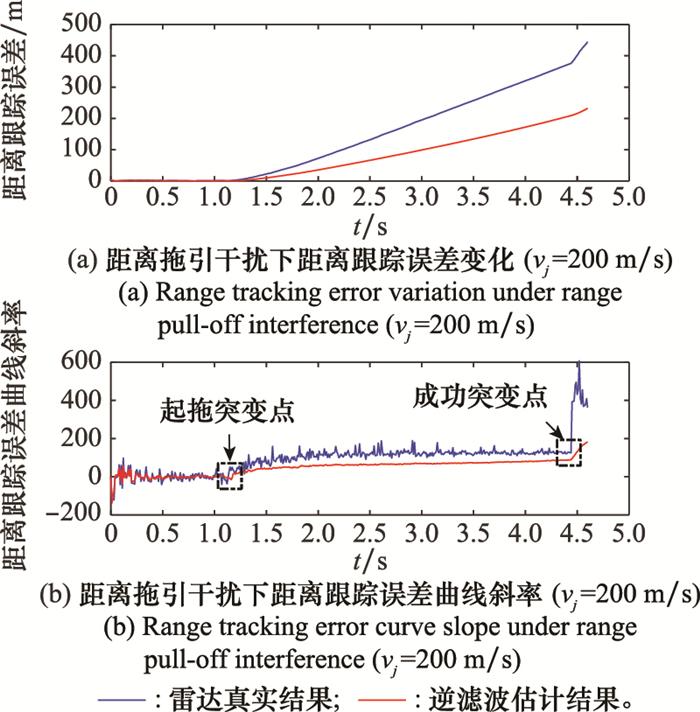
针对距离门拖引干扰, 雷达方可以通过跟踪波门移动速度变化率的分析识别拖引干扰, 然后采用记忆跟踪波门等方法对抗拖引干扰^[31], 造成拖引干扰失败。为了利用距离跟踪误差进行干扰效果判定, 本文根据距离拖引干扰原理定义了图 10所示的3类突变点: ①起拖突变点: 假设停拖期干扰信号能够成功捕获距离波门, A点时刻进入拖引期, 拖引干扰开始起效, 雷达距离跟踪误差会发生第1次突然增大, 将该点称为起拖突变点。②成功突变点: 拖引期出现起拖突变点后, 雷达跟踪误差将持续增大。如果跟踪波门在B点时刻被成功拖离真实目标回波, 雷达跟踪误差将发生第2次突然增大, 将该点记为成功突变点。③失败突变点: 如果在拖引期实施过程中, 由于拖引速度过大没有拖走跟踪波门或干扰被雷达成功识别, 雷达在C点时刻重新锁定跟踪上目标本体, 雷达跟踪误差会突然减小, 记该点为失败突变点。

跟踪误差突变点检测方法设计如下。

持续对估计跟踪误差曲线斜率$\hat{e}_{\text {rate }_k}$进行记忆, 计算当前k₁时刻为止的误差斜率均值:

(27) $\bar{e}_{{\text {rate }}_k}=\frac{1}{k} \sum\limits_{i=1}^k \hat{e}_{{\text {rate }}_k}$

进入拖引期后, 若从k₀时刻开始连续累计Δk_t个时刻点误差斜率均值比前一时刻误差斜率均值的增长量大于阈值γ_e1, 则将k₀+Δk_t－1时刻记为突增点, 记该时刻为k₁, 从k₁时刻开始重新计算距离误差均值, 即

(28) $\bar{e}_{{\text {rate }}_k}=\frac{1}{k-k_1+1} \sum\limits_{i=k_1}^k \hat{{\boldsymbol{e}}}_{{\text {rate }}_k}$

若在拖引期首次检测出突增点则为起拖突变点, 若在检测出起拖突增点后雷达跟踪误差持续增大, 并第2次检测出突增点, 则为成功突变点。

突降点检测与突增点检测方法类似, 对估计跟踪误差曲线斜率进行记忆, 计算曲线斜率均值, 当从某一时刻开始连续Δk_t次误差均值减小量大于阈值γ_e2, 则检测为失败突变点。

(3) 干扰效果在线评估及策略调整

基于突变点检测结果, 可以对干扰成功/失败及成功/失败时刻的干扰效果进行评估, 并根据评估结果调整干扰策略。干扰效果评估结果及干扰策略调整措施如表 1所示, 其中Ⅲ型失败是由于拖引速度过大导致在拖引初期干扰信号就脱离跟踪波门或被雷达抗干扰识别, 其余类型原因见上文。需要指出的是, 在线干扰策略调整是一个多要素约束条件下的受限优化问题, 由于本文重点为基于逆滤波处理的干扰效果在线评估方法设计, 在干扰策略调整方面做了简化处理, 即根据评估结果直接对拖引速度及关机时间做出调整。

本文仿真验证以主动寻的制导雷达导引头作为雷达方, 体制为脉冲多普勒雷达, 雷达导引头基于LQG控制理论^[32-33]确定的最优制导律带来的雷达位置状态变化, 作为雷达方动作。本文假设该雷达量测已由载机自身搭载的有源探测系统或外部辅助探测系统或通过侦干探通一体化技术支持得到。

假设雷达方对目标距离、速度信息进行滤波跟踪, 得出对相对状态x的最优估计$\widehat {\bf{x}} = \left[ {{{\hat r}_x}, {{\hat r}_y}, {{\hat r}_z}, {{\hat v}_x}, {{\hat v}_y}, {{\hat v}_z}, {{\hat a}_{tx}}, {{\hat a}_{ty}}, } \right.{\left. {{{\hat a}_{tz}}} \right]^{\rm{T}}} $, 其中r、v、a分别为目标对雷达的相对距离、速度、加速度。雷达导引头以最小化过载和脱靶量为目的根据LQG理论设计最优制导律^[32]为

(29) ${\boldsymbol{u}}=\left[a_{m x}, a_{m y}, a_{m z}\right]^{{\mathrm{T}}}=\left[C_1 {\boldsymbol{I}}_3, C_2 {\boldsymbol{I}}_3, C_3 {\boldsymbol{I}}_3\right] \hat{{\boldsymbol{x}}}$

式中: a_mx、a_my、a_mz表示雷达导引头在各方向上的加速度分量; 系数C₁, C₂, C₃分别如下:

(30) $\left\{\begin{array}{l}C_1=\frac{N}{t_{{\mathrm{go}}}^2} \\C_2=\frac{N}{t_{{\mathrm{go}}}} \\C_3=\frac{N\left[{\mathrm{e}}^{-\lambda t_{{\mathrm{go}}}}+\lambda t_{{\mathrm{go}}}-1\right]}{\left(\lambda t_{{\mathrm{go}}}\right)^2} \\t_{{\mathrm{go}}}=t_f-t\end{array}\right.$

式中: t_go表示飞行器剩余飞行时间; N为导航比。由式(29)可知, 在该制导律影响下, 导弹运动特性与弹目距离、导航比、飞行器剩余飞行时间有关, 且在导航比及剩余飞行时间一定的前提下, 导弹在x、y、z各方向上的运动加速度随跟踪距离的增大而增大。

由上可得, 对抗方在噪声中观测到的雷达动作为a = u + μ, 其中逆滤波模型量测矩阵C =[C₁I₃, C₂I₃, C₃I₃]。

具体对抗仿真在二维平面空间内进行, 场景为空-空对抗, 导弹迎头攻击载机目标, 雷达对目标进行距离、速度跟踪。以雷达初始位置为坐标原点建立直角坐标系, 导弹初始飞行速度为[400 m/s, 500 m/s], 目标初始时刻位于[1 000 m, 1 000 m], 沿x轴负方向做匀速直线运动, 速度为200 m/s。

雷达在杂波中利用PDA滤波器对目标进行跟踪, 距离波门宽度为脉宽的整数倍, 脉宽μ=5×10^－6 s。目标检测概率P_D=1, 目标落入波门内概率P_G=0.999 7。假设波门最大跟踪速度v_max=700 m/s。对抗方采取自卫式距离门干扰, 假设干扰在停拖期可以成功捕获距离跟踪波门, 干扰参数设置如表 2所示。

仿真中杂波体现为关联波门内的虚假测量点, 杂波生成方式与第2.2节相同, 仿真中每帧Δt=0.01 s。

实验从以下3个方面评价本文干扰效果评估方法的有效性和适用性。

(1) 在线干扰效果评估结果的正确性。若雷达方的真实情况与干扰方在线干扰效果评估结果相同, 评估正确, 反之评估错误。

(2) 在线干扰效果评估的时效性。采用干扰方得到评估结果时刻t₁与导引头真实受影响时刻t₀间的延迟Δτ=t₁－t₀, 评价该方法的时效性。

(3) 雷达跟踪误差估计的准确性。由于干扰效果评估以跟踪误差估计为基础, 因此跟踪误差估计RMSE能一定程度反映干扰效果评估的准确性。采用拖引期内干扰效果评估过程中的雷达跟踪误差估计RMSE值, 评价对抗方对雷达跟踪误差估计的准确度, 具体计算方法如下:

(31) ${\mathrm{RMSE}}\_ e=\sqrt{\frac{1}{L} \sum\limits_{k=1}^L\left(\hat{e}_k-e_k\right)}$

式中: e_k和$\hat{e}_k$为k时刻真实的雷达距离跟踪误差和对抗方对跟踪误差的估计值; L为计算时间区间内的仿真总帧数。

(1) 不同拖引干扰参数下的干扰效果评估

图 11~图 14所示为拖引速度为v_j={50, 200, 500, 700}m/s条件下的四组干扰效果评估结果, 实验中设置导引头导航比N=10, 杂波密度λ=0.000 1 s/m。

图 11所示为干扰效果评估结果为Ⅰ型失败时的干扰效果评估曲线, 由图 11可知, 当拖引速度为500 m/s时, 真实和估计跟踪误差曲线均在2.38 s时检测到失败突变点, 判断干扰失败, 说明当前拖引速度过大, 导致被雷达抗干扰模块识别或由于速度过大使得干扰信号脱离跟踪波门。图 12所示为Ⅱ型失败的干扰效果评估曲线, 可看出拖引期只检测到了起拖突变点, 说明当前50 m/s的拖引速度太小, 不足以使真实回波脱离雷达跟踪波门。

图 13所示为Ⅲ型失败的干扰效果评估曲线, 可以看出当前拖引速度过大, 初始时刻就被雷达抗干扰失败或干扰信号脱离跟踪波门或拖引速度超过雷达最大跟踪速度。如图 14为判定结果为成功的干扰效果评估曲线, 可看出在拖引期相继检测到起拖突变点和成功突变点, 说明当前200 m/s的拖引速度可以成功将雷达距离波门拖离目标回波。

表 3所示为拖引速度取50~700 m/s的7组实验结果。由表 3可知, 不同拖引速度下干扰效果定性评估结果均正确, 与真实干扰结果相同。

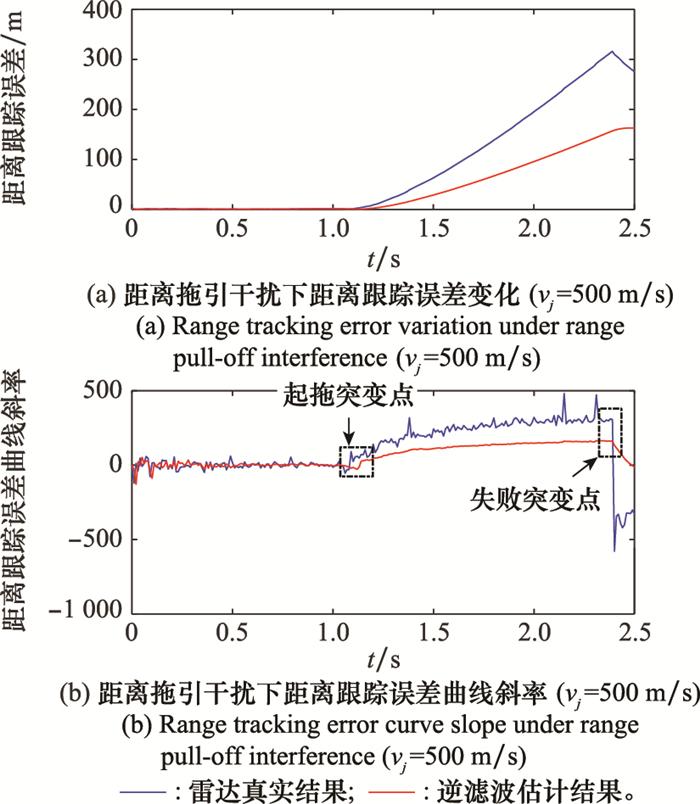
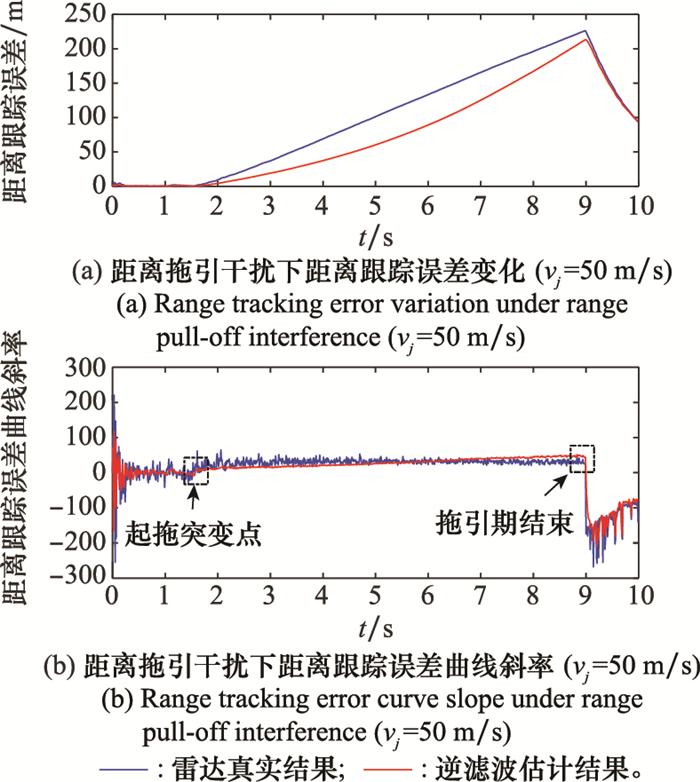
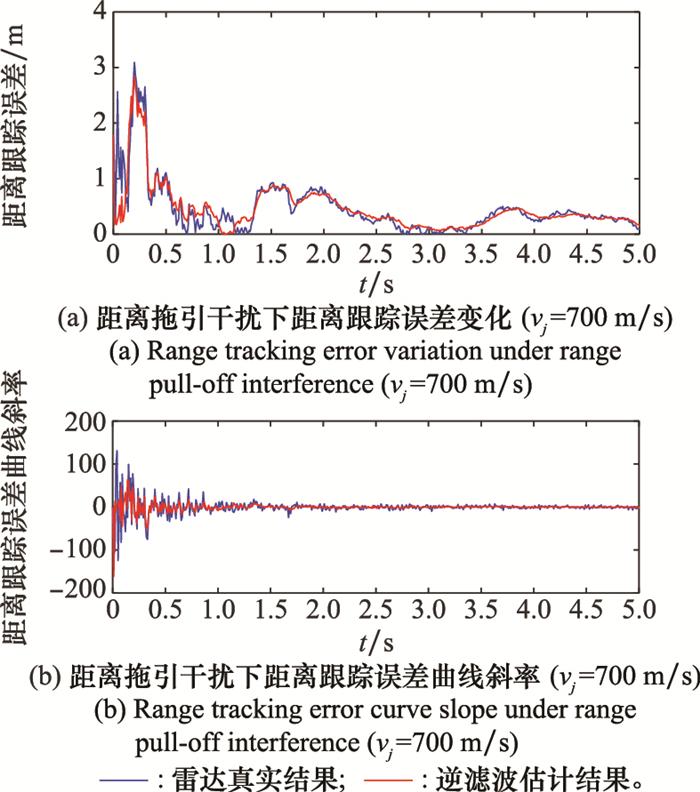
当拖引速度过小, 如50 m/s时, 干扰效果评估时延为0 s, 这是由于判定依据为直到拖引期结束还未出现成功/失败突变点, 因此判定时刻为拖引期结束时, 没有突变点检测引入的时延。当拖引速度取100~500 m/s时, 干扰成功/失败的判定均是由于在拖引期检测到成功/失败突变点, 因此会引入突变点检测的必要时延, 即突变点检测中累计判断时长, 仿真中设定检测中累计判定次数为Δk_t=3, 因此时延为0.02 s。当拖引速度为700 m/s时, 由于拖引期过半还没有检测到起拖突变点, 则没有由于突变点检测引入的时延, 但实际上从进入拖引期开始干扰便失败, 而判定时刻为拖引期中期, 因此判断时刻延迟拖引期时长的一半。此外通过分析距离跟踪误差估计的RMSE值可知, 尽管相比于第2.2节中无干扰下的估计RMSE有所增大, 但如表所示, 该范围内的RMSE增减未对干扰效果评估的正确性及时效性产生影响。

(2) 不同对抗方量测噪声的干扰效果评估

在拖引速度v_j=200 m/s, 雷达导引头导航比N=10的基础设置下, 令观测噪声均方差r_us取0~100的8组数值, 可得如表 4所示的实验结果。

由表 4可知，当量测噪声均方差在0~100内时, 干扰效果定性评估结果均正确。干扰效果评估时延和跟踪误差估计RMSE会随对抗方量测噪声均方差的增大而增加。当量测噪声均方差较小时, 干扰效果评估时延的来源仅为突变点检测中的累计判断时长。

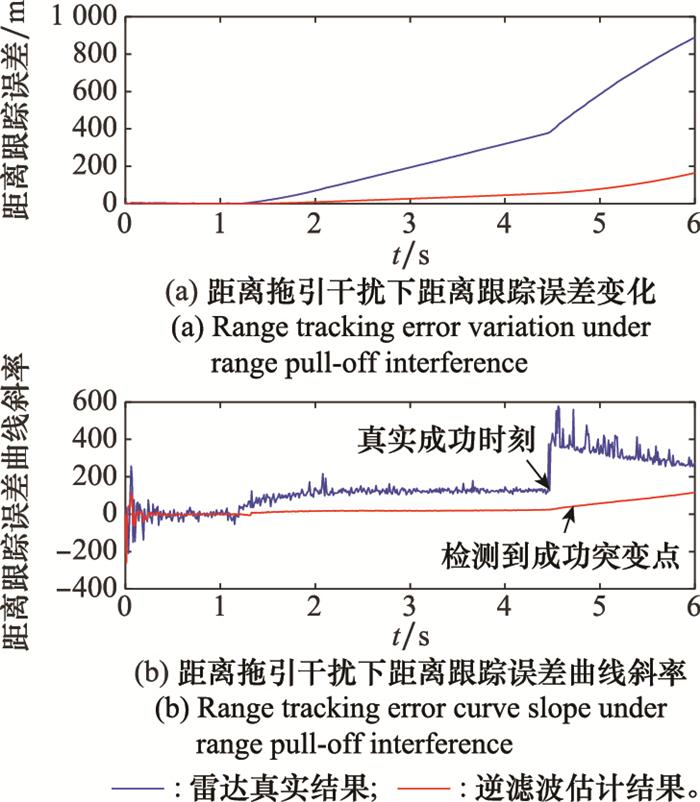
当量测噪声均方差为10时有如图 15所示的仿真结果。

由图 15可知, 此时成功突变点变得更加“不明显”, 需等到误差斜率均值增大到一定阈值才可判定成功, 因此当量测噪声均方差大于10时, 评估时延不仅来源于突变点检测中的必要时延, 还包括由于突变点“不明显”导致的检测滞后。且该时延随着量测噪声均方差的增大而增加, 对应的跟踪误差估计RMSE也会增大, 当时延增大到一定程度后, 将导致在拖引期内始终未检测出成功突变点, 判定干扰失败, 导致评估结果错误。经实验, 当量测噪声均方差在正常范围内时不会出现上述情况, 因此能保证干扰效果评估的正确性。

(3) 不同雷达动作参数下的干扰效果评估

在拖引速度v_j=200 m/s, 对抗方量测噪声均方差为r_us=0.1 m的条件下, 改变雷达动作参数, 在本节所设置的仿真场景中主要体现为雷达导引头的导航比, 令导航比从0.1增大到5进行如表 5所示的7组实验。

由表 5可知, 雷达导引头导航比越大, 干扰效果评估时延和跟踪误差估计RMSE越小。当雷达导引头导航比小于1时, 评估时延和跟踪误差估计RMSE稍大, 但仍能保证评估结果的正确性。当导引头导航比大于1时评估时延小于1 s。且导航比只需大于3即可保证干扰效果评估方法没有除突变点检测必要时延外的其他时间延迟, 保证干扰效果评估的强时效性。

综上所述, 本文所提出的基于逆滤波处理的RGPO效果评估方法适用于不同拖引速度下的RGPO效果评估。干扰效果评估的正确性、时效性及距离跟踪误差估计准确性与对抗方的量测噪声和雷达动作参数有关。随着量测噪声均方差增大和导航比的减小, 干扰效果评估的时间延迟和跟踪误差估计RMSE增大, 增大到一定程度可能导致干扰效果定性评估结果错误。经仿真实验可知, 当对抗方量测噪声均方差小于100, 雷达导引头导航比大于0.1时, 干扰效果评估结果均正确。且当量测噪声均方差小于30, 雷达导引头导航比大于等于1时, 在干扰效果评估结果正确的基础上, 可保证干扰效果评估的强时效性和距离跟踪误差估计的准确性。

(4) 基于干扰效果评估的距离拖引干扰策略调整仿真实验

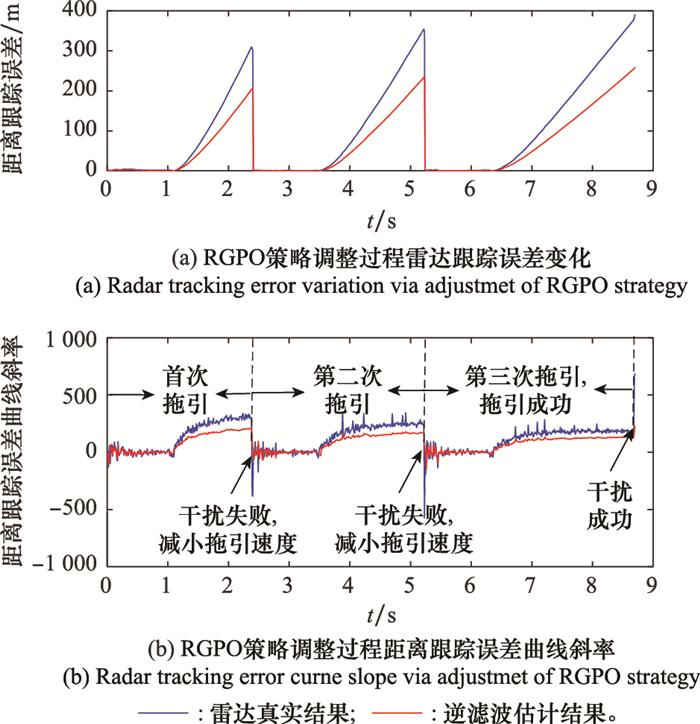
本实验验证如本文第3.2节所述的距离拖引干扰策略改进方法, 仿真设置初始拖引速度为500 m/s, 结果如图 16所示。

由图 16可知, 仿真开始以500 m/s的拖引速度进行首次干扰, 于2.4 s检测到失败突变点, 判定干扰失败, 根据策略调整方案需要停止拖引并减小拖引速度。减小拖引速度为400 m/s后开始实施第2次干扰, 但此时拖引速度仍较大, 导致干扰信号在5.22 s再次脱离雷达距离跟踪波门, 对抗方在5.24 s检测到失败突变点并停止干扰。再次减小拖引速度到300 m/s后实施第3次干扰, 在8.7 s时检测到成功突变点, 判定干扰成功。由图 16可知, 在第1次干扰周期内基于干扰效果在线评估结果调整干扰策略后进行了第2次拖引干扰, 并在第2次拖引干扰周期内根据本次评估结果调整拖引速度参数及关机时间, 实施第3次距离拖引干扰后干扰成功。本实验表明, 本文所提方法可实现非合作对抗过程中的干扰效果在线即时评估, 并通过在线调整策略达到成功干扰的目的。

本文针对非合作雷达干扰效果在线评估问题, 提出了基于逆滤波处理的干扰效果在线评估方法并基于此对干扰参数进行实时优化。本文首先对逆滤波处理估计雷达跟踪误差问题进行建模, 推导仿真了杂波背景下雷达滤波的逆滤波处理算法。然后, 基于逆滤波处理提出了适用于破坏雷达跟踪状态的干扰类型的干扰效果在线评估方法。最后以针对导引头雷达的自卫式RGPO为例, 仿真验证了该方法的可行性和有效性。本文所提干扰效果在线评估方法是通过逆信号处理实现雷达系统更多内部状态感知和推理的一次有益探索, 但在对抗条件方面作了相应假设并在干扰策略调整方面做了简化, 后期将在更宽松的假设下对更多雷达内部环节的逆处理方法开展研究。