0 引言
结合实际作战环境, 舰空导弹在试验过程中, 其性能受多种因素的影响, 这些因素既包括定量因素, 如靶标的距离、高度、速度、遭遇距离、航路捷径等, 也包括定性因素, 如靶标种类、干扰样式等。同时存在的定性-定量因子给舰空导弹补充试验设计增加了不小的难度。当前, 补充试验设计方法主要可分为基于输入的试验设计方法和基于输出的试验设计方法。其中, 基于输入的试验设计方法主要有随机抽样法[3-4]、低差异序贯法[5]、嵌套拉丁超立方体设计法[6-7]、泰森多边形抽样法[8]、蒙特卡罗抽样法[9-10]、均方误差(mean square error, MSE)法等方法[11]; 基于输出的试验设计方法主要为贝叶斯优化法[12]、黄金分割法[13]、局部线性近似-泰森(local linear approximation-Voronoi, LOLA-Voronoi)方法[14]等, 其中贝叶斯优化法主要用于黑箱函数极值搜索, 而黄金分割法和LOLA-Voronoi方法无法利用代理模型在样本信息利用上的优势, 补充试验设计效果不稳定。
上述基于输入的试验方法仅使用当前试验样本的位置来确定下一步的采样位置, 不考虑输出响应值的影响, 一味追求样本分布的均匀性, 对试验空间重点区域的开发考虑不足; 而基于输出的试验设计方法同时兼顾了输入和响应对采样的共同影响, 通过构建近似梯度来平衡采样中的探索与开发(LOLA-Voronoi方法), 不依赖代理模型。但是, 对于某些具有有效先验知识的采样空间而言, 构建代理模型可提高搜索效率, 相比于通过近似梯度进行补充试验的设计方法, 基于模型的补充试验设计方法可有效改善试验结果的适用性[15-16]。此外, 目前对基于模型的补充试验设计方法的研究的主要关注点仍在定量因子设计, 对混合定性-定量因子的试验设计的研究较少。与仅包含定量因子的预测评估模型相比, 定性-定量因子混合的预测评估模型有其自身特点, 探索定性-定量因子混合预测评估模型基础上的补充试验设计方法具有一定价值。
事实上, 类似舰空导弹的复杂装备在试验方案设计中面临的问题普遍存在, 本文针对当前补充试验设计方法在处理包含定性-定量因子方面存在的不足, 研究了一种混合定性-定量因子模型的补充试验设计方法。该方法首先构建了定性-定量因子混合评估模型。然后, 利用探索-开发平衡策略进行补充试验设计建模, 并在此基础上确定目标试验点与最佳邻域, 再借助遗传算法搜索出最佳邻域位置。最后, 通过示例对所提出的模型和方法进行了验证。
1 定性-定量因子混合评估建模
假设需要进行的补充试验设计中, 试验输入既包含定性因子, 又包含定量因子, 可以表示为w=(xt, zt)t, 其中x= (x1, x2, …, xm)t表示m个定量因子, z=(z1, z2, …, zJ)t表示J个定性因子。
假设已获得n组试验数据, 在此基础上构建高斯过程模型:
式中: 未知系数向量为β, β =(β1, β2, …, βl)t, 相关函数向量为f(w), f(w)=(f1(w), f2(w), …, fl(w))t, 两者相乘组成高斯过程模型的回归项; ε(w)~GP(0, σ2)是满足均值为0、方差为σ2的高斯过程残差项。
由上可知, 残差项ε(w)~GP(0, σ2)中相关函数的构建是关键。与定量因子相关函数的构建方法不同, 定性因子中并没有“距离”的概念, 因此, 基于距离的相关函数方法对定性因子并不适用[17]。为此, 需要建立既包含定性因子, 又包含定量因子的相关函数模型。
为了便于理解相关函数的构建过程, 首先构建仅包含一个定性因子的相关函数模型。设定性因子z1具有I1等级类别水平, 进一步, 令εu(w)=ε((xt, ut)t), u=1, 2, …, I1, 可进一步得到:
由式(2)可知, 仅需要定义ε*(x)的相关函数和互相关函数即可。为了便于后续计算, 假设ε*(x)=Aη(x)。其中, A=(a1, a2, …, aI1)是一个具有单位行向量的I1×I1的非奇异矩阵(即当u=1, 2, …, I1时, 向量乘积autau=1);η(x)=(η1(x), η2(x), …, ηI1(x))t。其中, η1(x), η2(x), …, ηI1(x)为具有相同方差σ2和相关函数Kϕ的独立随机过程。由此可知, corr (η(xi), η(xj))=Kϕ(xi, xj)II1。其中, II1是一个I1×I1的单位矩阵。对于任意两个输入wi和wj, 其相关函数可定义为
令τr, s=artas, 其中, r, s=1, 2, …, I1, 可进一步得到定性因子相关矩阵T1=(τr, s)=AAt, 这是一个具有单位对角元素的正定矩阵。由上可知, 对于任意单位对角元素的正定矩阵T1=(τr, s)和任意相关函数Kϕ(xi, xj), 式(3)中的相关函数可进一步写为corr(ε(wi), ε(wj))=τz1i, z1jKϕ(xi, xj)。其中, τz1j, z1i=τz1i, z1j描述等级类别z1j和z1i的互相关性。定量因素响应模型构建相同, Kϕ(xi, xj)的构建仍然选用高斯核函数。因此, ε(wi)和ε(wj)的相关函数可进一步表示为
由式(4)可知, τz1j, z1i互相关模型的构建和求解是定量-定性因子混合响应模型构建的关键。目前, 常用的解决方法包括可交换相关函数法、乘法相关函数法、组相关函数法、序数定性因子相关函数法和超球面分解法等。相比而言, 超球面分解法常用来描述复杂估计过程模型中的相关性, 可以用投影的方式直观表现定性因子的位置关系[18], 可有效克服其他方法未知参数多、推导困难、计算量巨大的缺点, 便于理解和计算。因此, 本文选用超球面分解法进行定性因子相关性建模, 主要分以下两步进行。
步骤1 已知T1=(τr, s)是一个具有单位对角元素的正定矩阵, 对其进行Cholesky分解, 可得
式中: L={lr, s}为具有严格正对角项的下三角矩阵。
步骤2 对下三角矩阵L={lr, s}的每个行向量[lr, 1, lr, 2, …, lr, r]进行描述, 将其定义为一个多维单位超球面上的坐标, 如下所示:
式中: θr, s∈(0, π)。由此可知, 对角矩阵L={lr, s}中对角线中元素lr, r均为正值, 可进一步推导, L={lr, s}为正定矩阵。此外, 式(6)中
当J=1时, T1=1, 即与仅包含定量因素的相关函数构建方法相同。
当J=2时,
进一步构建多维单位球面坐标, 可得
由l2, 1≥0可知, θ2, 1∈(0, π), 计算方法如下所示:
当J=3时,
其中, l1, 2=l2, 1, l1, 3=l3, 1, l3, 2=l2, 3; 进一步构建多维单位球面坐标可得
式中: θi, j∈(0, π)。计算方法如下所示:
当定性因素数目u>1时, 构造任意两个输入的相关函数模型:
与定量因素预测响应模型构建相似[18], 定量-定性因素混合预测响应模型中包含的未知相关系数为ϕ和θ。
任意未知输入w0的预测响应模型为
式中: rt(w0)=(corr(ε(w0), ε(w1)), corr(ε(w0), ε(w2)), …, corr(ε(w0), ε(wn))); F=(f(w1), f(w2), …, f(wn)); R是包含所有corr(ε(wr), ε(ws))(r, s=n)的相关函数矩阵。
与定量因素预测响应模型中未知参数估计值的求取方法相似[19], 利用极大似然估计可进一步求得
2 补充试验模型构建
假设当前已获得的试验响应值构成的样本集合为N={W=(w1, w2, …, wn)t, Y=(y1, y2, …, yn)t}, 在该样本集合中依次选择一组试验样本(wi, yi)(其中i=1, 2, …, n)作为验证样本, 利用交叉验证方法对模型预测精度进行评估验证, 预测值均方根误差(root mean square error, RMSE)为
式中: 当RMSE(n)≤δ时, 初始样本数量满足对预测模型精度的要求, 不需要再进行补充试验设计; 当RMSE(n)>δ时, 初始样本数量无法满足对预测模型精度的要求, 需要进行后续补充试验设计。其中, δ为预测精度误差允许值。
当预测响应模型的预测精度无法满足要求时, 需要增加试验样本的数量来提高预测模型的准确性, 在满足预测精度的前提下尽可能少地补充试验样本点, 是补充试验模型构建的关键。由预测模型构建的基本特征可知, 在进行补充采样时, 应对两个因素进行平衡, 这两个因素分别为探索和开发。探索是对全局未开发区域不确定性的度量; 开发是对感兴趣区域的度量。为此, 本文在已构建预测响应模型的基础上设计补充试验。
2.1 探索
由上文可知, 预测点的不确定性由预测均方差表示, 预测均方差的大小表征着预测结果的不确定性。在进行补充试验时,应探索选择预测均方差较大的点, 以降低预测值的不确定性, 提高预测模型的稳定性。
对于同时包含定性-定量因子的试验, 对任意未测点w, 该未测点的预测均方差(mean square error of prediction, MSEP)可表示为
利用多元正态条件分布可知:
式中: μ1是一个m×1向量; μ2是一个n×1向量; Σ1, 1是一个m×m矩阵; Σ1, 2=Σ2, 1t是一个m×n矩阵; Σ2, 2是一个n×n矩阵,则可以得到条件分布[W1|W2]为
由于[y(w), Y]均满足多元正态分布的条件, 利用多元正态条件分布公式可进一步推导出:
式中: MSEP为
式中: F=(f(w1), f(w2), …, f(wn)); Rw是包含所有corr(ε(wr), ε(ws))(r, s=n)的相关矩阵; rw=(corr(ε(w), ε(w1)), corr(ε(w), ε(w2)), …, corr(ε(w), ε(wn)))t; fw=f(w)。
通过构建MSEP模型可以对任意未测点进行MSEP估计, 并且可以通过优化算法找出MSEP最大的点, 并在该位置进行补充试验。通过观察MSEP可知, 未测点MSEP的取值只与输入有关, 与响应值无关。因此, 在进行补充试验时, 每组试验均可以补充多个样本点。
2.2 探索-开发
现实中存在着某些响应曲面局部难以近似的问题, 在补充试验中需要对该区域进行更加深入的开发, 以进一步提高预测模型精度。与文献[12]中的局部线性近似(local linear approximation, LOLA)方法不同, 本节考虑预测模型评估值对局部区域的描述, 在此基础上研究探索-开发策略。基于构建的评估预测模型, 探讨补充试验设计新方式。实现过程分为以下3步: 在当前样本空间中确定出目标试验点; 构建目标试验点的最佳邻域; 通过极大化MSEP在邻域中搜索补充样本点。
步骤1 确定包含重点区域的目标试验点。已知当前已获得试验样本空间为N, N={W=(w1, w2, …, wn)t, Y=(y1, y2, …, yn)t}, 依次将试验点{wi, yi}作为候选目标点, 利用样本空间中的剩余试验样本构建预测响应模型, 并对该候选目标试验点wi的预测值和MSEP进行求解。
式中: i=1, 2,…, n。
在此基础上, 给出目标试验点wi的预测误差(prediction error, PE), 分别为
由上可知, 目标试验点是由探索项和开发项共同确定的, 因此, 计算出每个候选目标试验点的MSEP和PE, 并将MSEP与PE相加的和作为候选目标试验点的得分, 将得分最高的点作为搜索的目标试验点, 如下所示:
步骤2 构建目标试验点的最佳邻域。由式(15)确定目标样本位置后, 接下来就需要构建最优目标邻域。
为不失一般性, 将最佳邻域中试验点的数量确定为d=2m, 其中m为定量因素的数目。依照定性因子对当前试验样本空间进行划分, 可得目标样本点邻域中试验点的数量为k, 则候选邻域的数目为Ckd。与LOLA方法中构建邻域的方式相似[14], 设定N(wobj, i)=(wi, 1, wi, 2, …, wi, m)表示目标试验点wobj的第i个邻域, 在此基础上获得多定量和单定量条件下的交叉多面体比率。
在多定量条件下,有
式中: pr表示候选目标试验点wobj中的定量N(因子xobj; pr)表示候选邻域; C(N(pr))表示候选邻域的内聚值; A(N(pr))为候选邻域的黏合值。
在单定量条件下,有
接下来给出候选邻域的分数:
对S(N(pr))按照分数值大小进行排序, 选出最优邻域。接下来,在邻域范围内搜索出新样本的位置, 完成补充试验设计。
步骤3 利用构建的MSEP模型在邻域中搜索下一个补充样本点。
已知邻域N(pr), 就可以确定邻域取值范围Vobj, 并在此基础上利用上文构建的MSEP模型, 搜索最优值作为补充试验输入。
由式(14)可知:
在邻域取值范围Vobj内, 利用遗传算法搜索出MSEP的最大值:
将式(16)作为第一组补充试验输入值, 然后将该值分别代入式(8)计算补充试验输入条件下的预测响应值, 并将该试验点补充到当前试验样本空间, 继续迭代上述过程, 直至达到该批试验次数要求。在此基础上, 将上述补充试验设计点代入响应模型, 并获得对应的响应值。
将所有的数值模拟试验数据补充到试验样本空间, 重新构建评估模型, 然后利用式(11)中的交叉验证方法对模型预测精度进行评估验证, 判定评估精度是否满足要求, 以确定是否需要继续进行补充试验。
3 算例分析
算例1
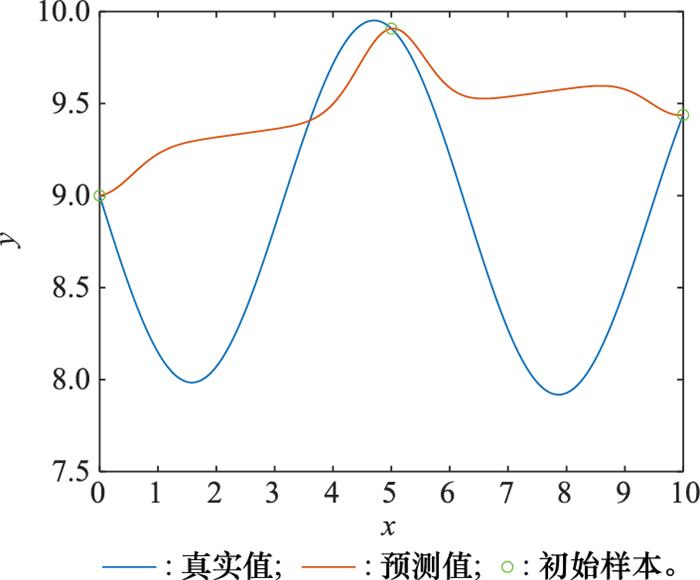
图1
图1
为均匀试验设计的3组初始样本点
Fig.1
Three groups of initial sample points for uniform test design
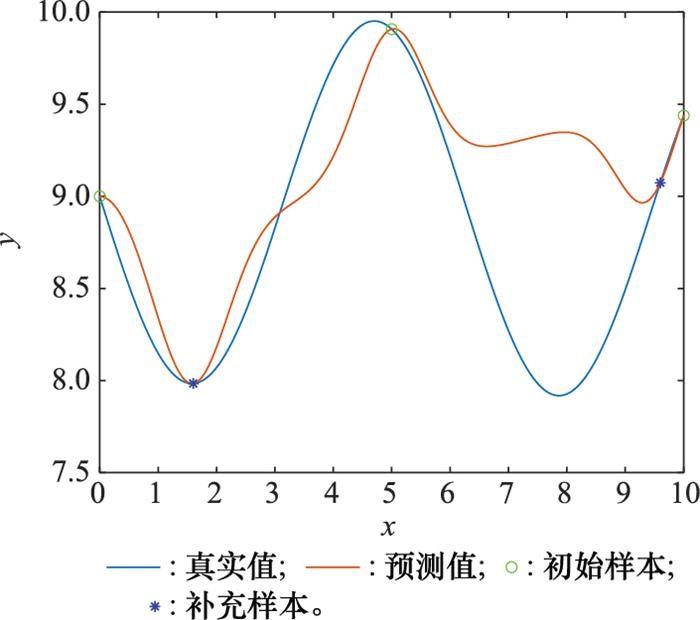
图2
图2
MSE方法补充的2组试验样本点
Fig.2
Two groups of test sample points supplemented by MSE method
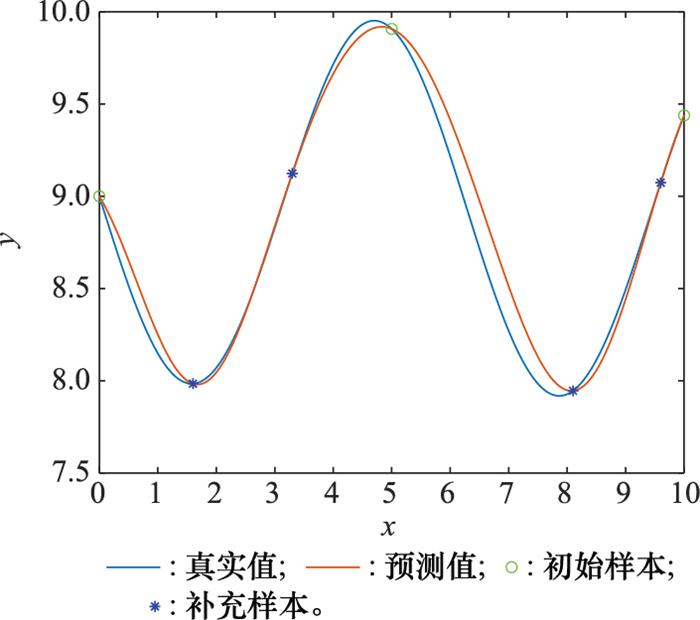
图3
图3
MSE方法补充的4组试验样本点
Fig.3
Four groups of test sample points supplemented by MSE method
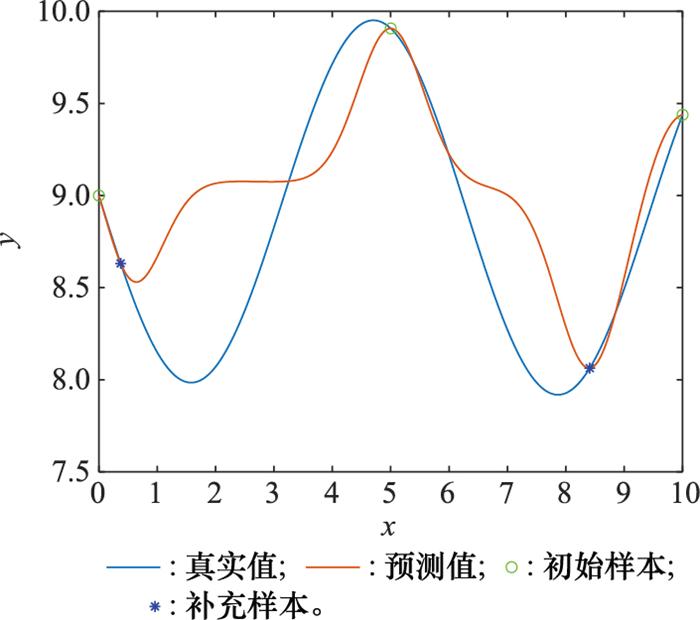
图4
图4
所提方法补充的2组样本点
Fig.4
Two groups of sample points supplemented by the proposed method
图5
图5
所提方法补充4组样本点
Fig.5
Four groups of sample points supplemented by the proposed method
图6
算例2
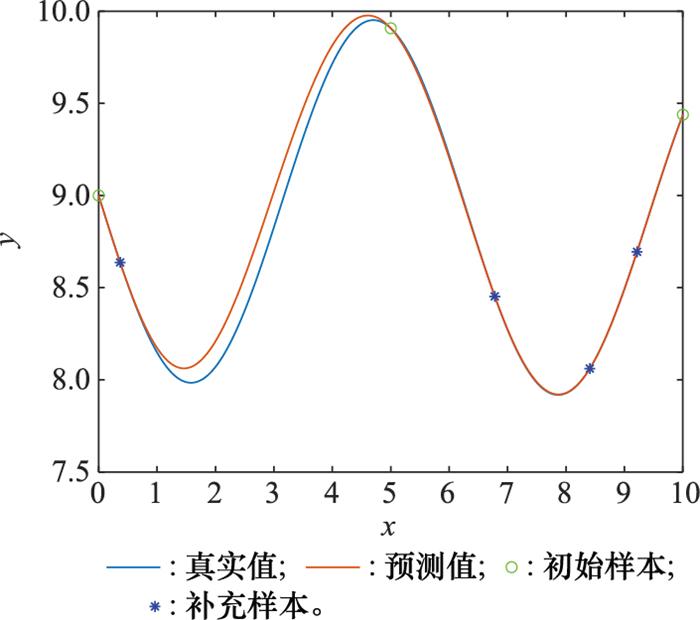
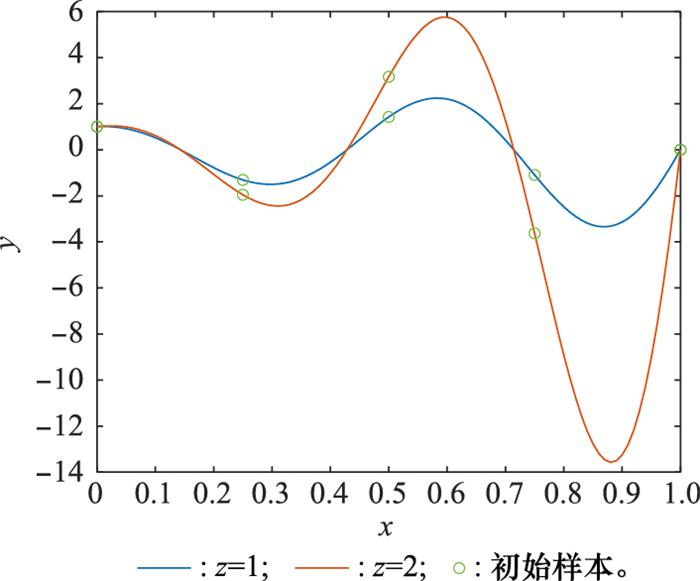
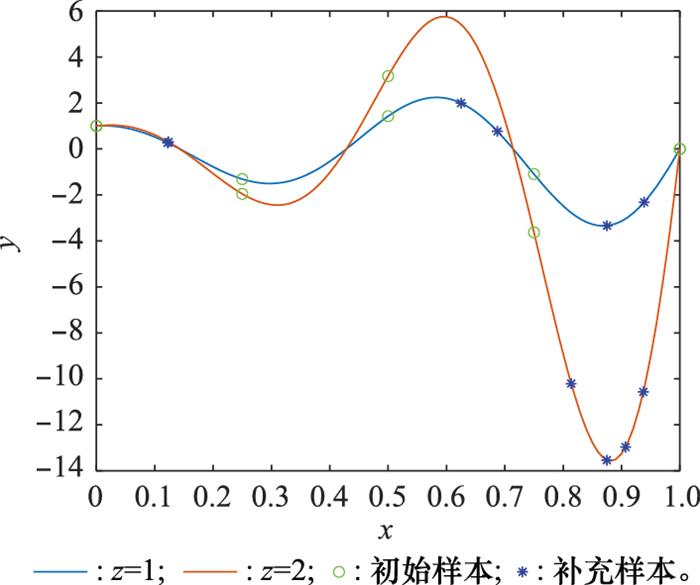
在数值算例2中, 测试函数包含一个定量因素和一个定性因素, 其中定性因素包含两个水平。首先, 利用均匀试验设计获得10个初始样本, 如图 7所示。
图7
图8
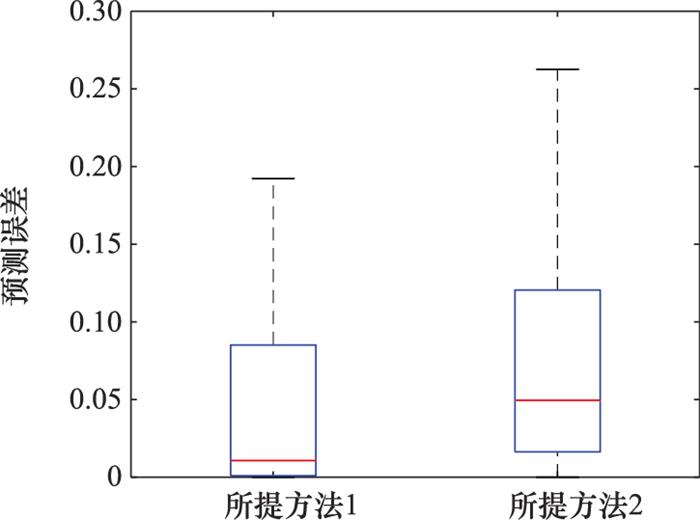
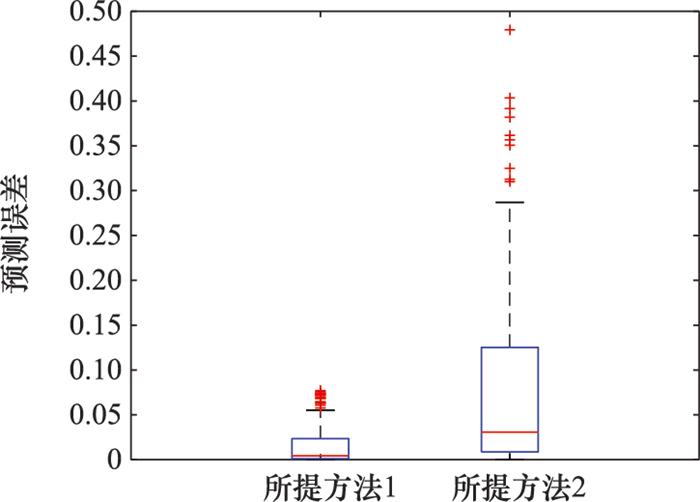
图9
图 9为预测误差箱型图。分析结果表明, 本文所提方法对于解决定性-定量因子混合补充实验设计问题, 对精度的改善效果更好。
4 示例研究
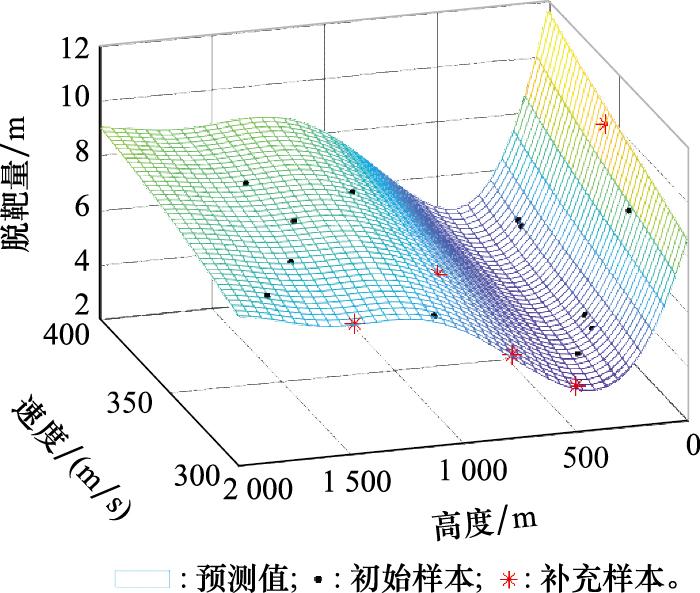
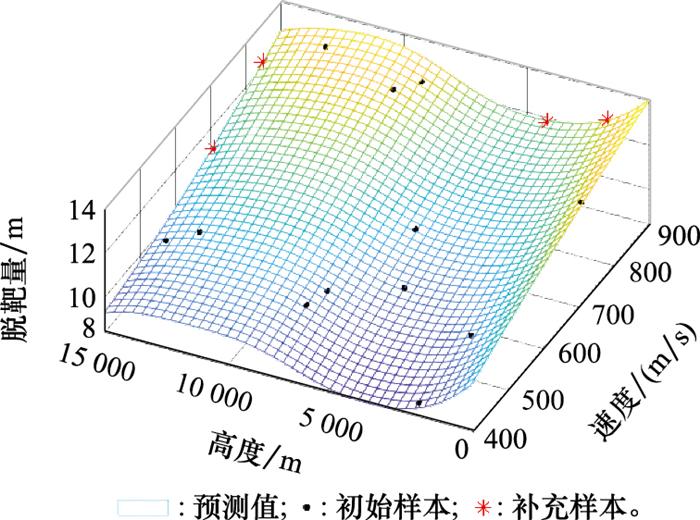
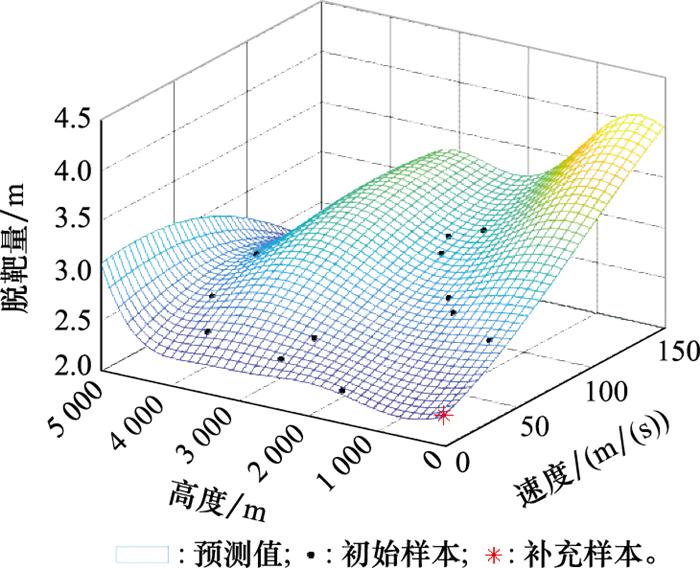
舰空导弹是舰艇主要的防空武器, 其作战性能受到目标、背景、干扰等复杂战场环境的影响, 涉及多个定性和定量因子。为了更好地验证本文所提方法的有效性, 下面对某型舰空导弹的试验影响因素进行抽象和简化, 在假设其他影响因素固定的前提下, 仅考虑目标因素的影响。选择脱靶量为响应值, 靶标类型、靶标速度和靶标高度为影响因子, 其取值范围如表 1所示。
表1 试验因子范围
Table 1
| 靶标种类 | 靶标速度/(m/s) | 靶标高度/m |
| 亚音速飞弹 | 300~400 | 10~2 000 |
| 常规飞机 | 400~900 | 50~15 000 |
| 直升飞机 | 0~150 | 30~5 000 |
表2 补充试验结果
Table 2
| 靶标种类 | 靶标速度/(m/s) | 靶标高度/m |
| 亚音速飞弹 | 300.61 | 1 484.26 |
| 亚音速飞弹 | 356.40 | 23.77 |
| 常规飞机 | 849.17 | 14 977.19 |
| 亚音速飞弹 | 302.04 | 772.24 |
| 直升飞机 | 0.41 | 33.27 |
| 常规飞机 | 703.65 | 14 889.13 |
| 常规飞机 | 899.59 | 1 704.10 |
| 常规飞机 | 897.69 | 4 139.37 |
| 亚音速飞弹 | 329.14 | 936.84 |
| 亚音速飞弹 | 301.45 | 497.26 |
图10
图11
图12
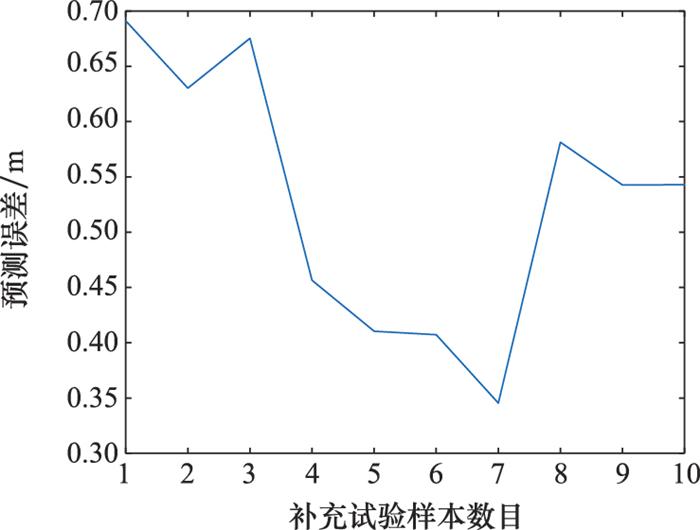
进一步, 利用交叉验证方法对补充试验后的模型预测精度进行验证, 模型预测误差如图 13所示。
图13
由图 13可知, 在补充试验过程中, 预测误差随样本数目的增加表现为非单调性递减的特征, 这与补充试验的探索特性有关。当补充试验点的位置处于某些关键未知区域时, 交叉验证误差会出现增加的情况, 试验结果与补充试验设计方法期望的探索方式一致。
5 结束语
本文结合舰空导弹等复杂装备在补充试验方案设计中存在的问题, 基于定性-定量因子混合模型, 提出了改善预测模型精度的补充试验设计方法。该方法主要平衡了对补充试验空间的探索与开发, 增强了捕捉重要特征样本位置的能力, 改善了预测模型的构建精度。通过算例分析, 验证了本文提出的补充试验设计方法的有效性。最后, 结合某型舰空导弹的补充试验方案设计对方法进行了深入的验证和分析。事实上, 影响舰空导弹等复杂装备的试验因素包含定性因素和定量因素是常态, 并且影响因素数量很多, 甚至因素间存在复杂的约束关系, 这就给模型的复杂度以及算法的求解效率提出了更大的挑战。本文仅是针对此类问题进行了初步的探索, 以最大限度地提高对试验对象性能描述的准确性, 后续将结合实际工程问题进行更加深入的研究。
参考文献
An iterated local coordinate-exchange algorithm for constructing experimental design for multi-dimensional constrained spaces
[J].DOI:10.23919/JSEE.2021.000103 [本文引用: 1]
The combat application of queuing theory model in formation ship to air missile air defense opera tions
[J].DOI:10.1088/1742-6596/1570/1/012083
Quantile regression for large-scale application
[J].
A statistical perspective on algorithmic leveraging
[J].
An efficient algorithm for constructing optimal design of computer experiment
[J].DOI:10.1016/j.jspi.2004.02.014 [本文引用: 1]
Nested latin hypercube design
[J].DOI:10.1093/biomet/asp045 [本文引用: 1]
Sequential design and ana-lysis of high-accuracy and low-accuracy computer codes
[J].DOI:10.1080/00401706.2012.723572 [本文引用: 1]
Efficient space-filling and non-collapsing sequential design strategies for simulation-based modeling
[J].DOI:10.1016/j.ejor.2011.05.032 [本文引用: 1]
基于BOX-COX变换的桥梁结构地震易损性分析
[J].
Seismic vulnerability analysis of bridge structure based on BOX-COX transformation
[J].
知识驱动的SSVEP刺激界面序贯式实验方案优化
[J].
Knowledge-driven optimization of sequential experimental scheme for SSVEP stimulus interface
[J].
Chemically doped fluorescent carbon and graphene quantum dots for bioimaging, sensor, catalytic and photoeletronic applications
[J].DOI:10.1039/C5NR07579C [本文引用: 2]
A novel hybrid sequential design strategy for global surrogate modeling of computer experiments
[J].DOI:10.1137/090761811 [本文引用: 1]
Hierarchical nonlinear approximation for experimental design and statistical data fitting
[J].
考虑变幂数的畸变动力学相似试验模型设计方法即试验研究
[J].
Design method of distorted dynamics similitude experimental model considering variable power and experimental study
[J].
A simple approach to emulation for computer model with qualitative and quantitative factors
[J].DOI:10.1198/TECH.2011.10025 [本文引用: 1]