箔条干扰作为一种常见的雷达无源干扰手段, 在1973年海战中被首次投入使用, 由于其具备干扰效果显著、干扰实施便捷和干扰成本低廉的优势, 现已被广泛应用于电子对抗(electronic countermeasures, ECM)[1 ] 。箔条弹打出后抛撒在空中,通过扩散形成具有一定长度、宽度和厚度的云状干扰物, 称为箔条走廊[2 ] 。箔条本身没有动力, 完全依靠自然扩散, 以箔条走廊尺寸、谱宽的稳定性为依据, 将扩散过程分为正在扩散状态和完全扩散状态[3 ] 。以箔条弹打出位置是否与目标在同一波束内为依据,分为质心式和冲淡式, 质心式箔条干扰可以近距离利用箔条走廊遮盖并保护目标; 冲淡式干扰的箔条走廊可以在远距离处形成诱饵[4 -5 ] 。文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的。
针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] 。第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标。
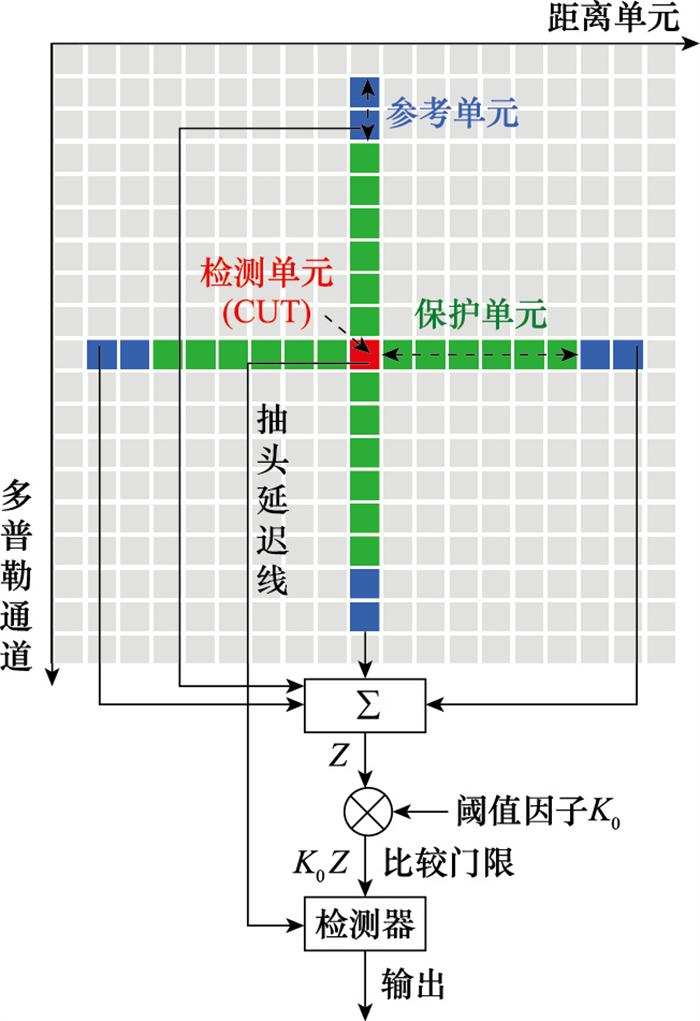
图1
2D-CFAR原理框图
Fig.1
Principle block diagram of 2D-CFAR
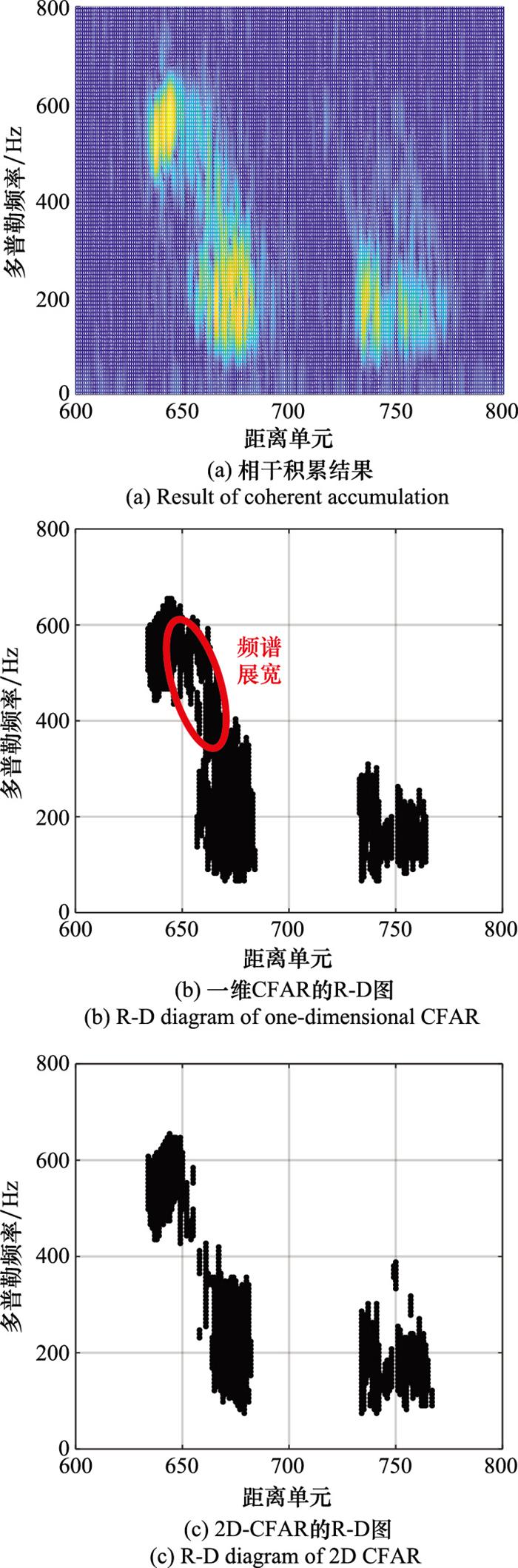
图2
一、二维CFAR结果对比
Fig.2
Comparison of the results of one-dimensional CFAR and 2D-CFAR
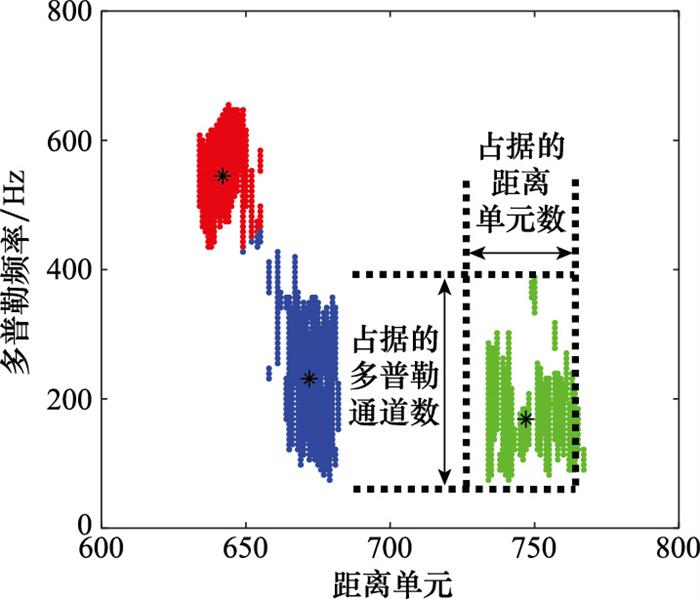
图3
MS算法聚类结果
Fig.3
Clustering result of MS algorithm
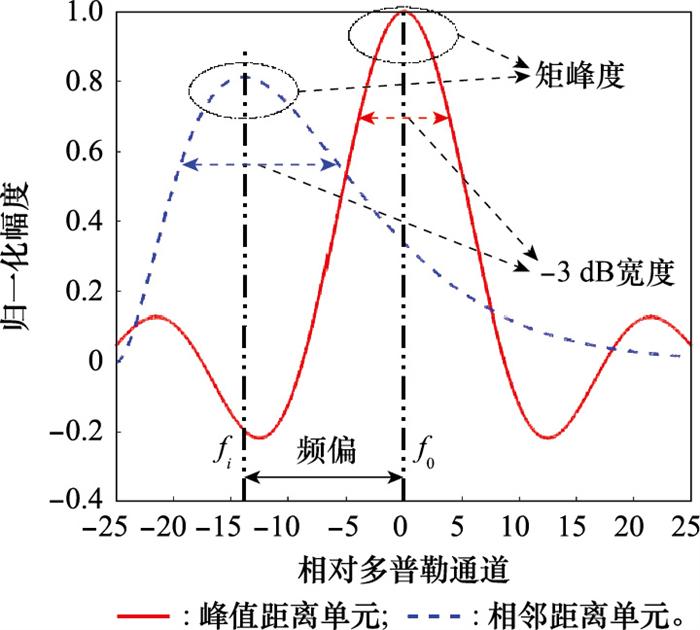
图4
频谱的特征信息
Fig.4
Characteristic information of the spectrum
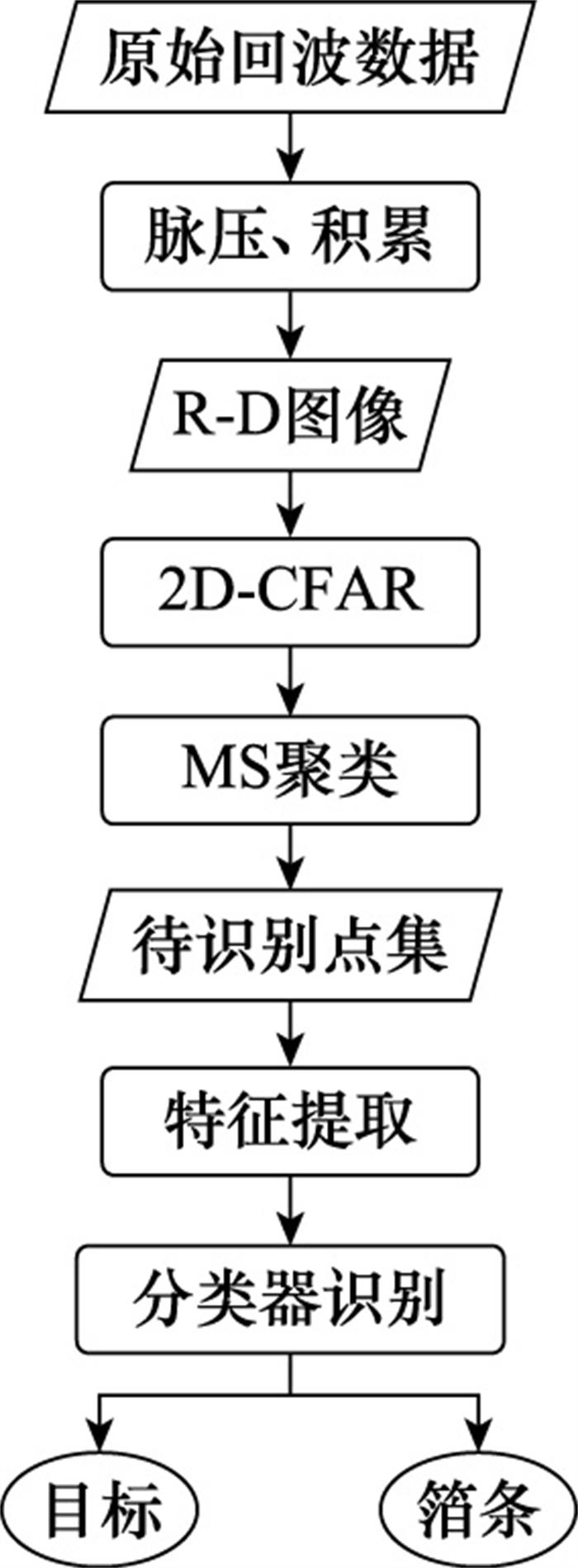
图5
数据处理流程
Fig.5
Procedure of data processing
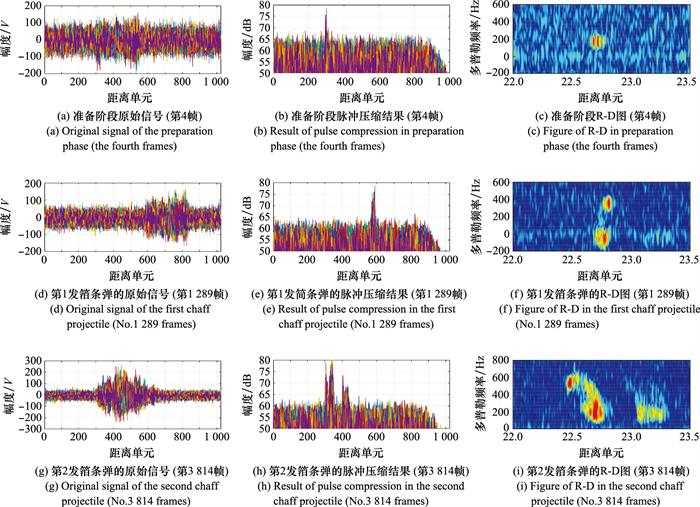
图6
传统雷达信号处理结果
Fig.6
Results of traditional radar signal processing
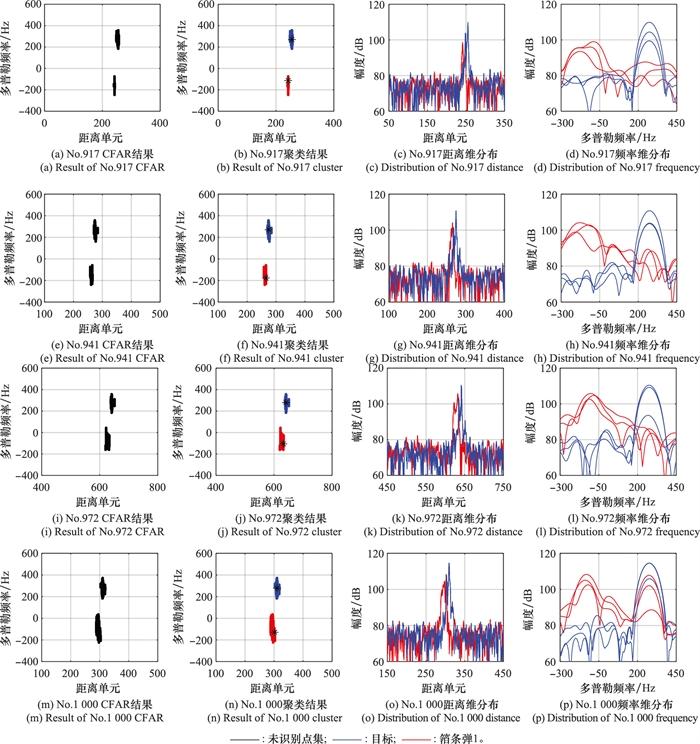
图7
第1发箔条弹的扩散过程
Fig.7
Diffusion process of the first chaff projectile
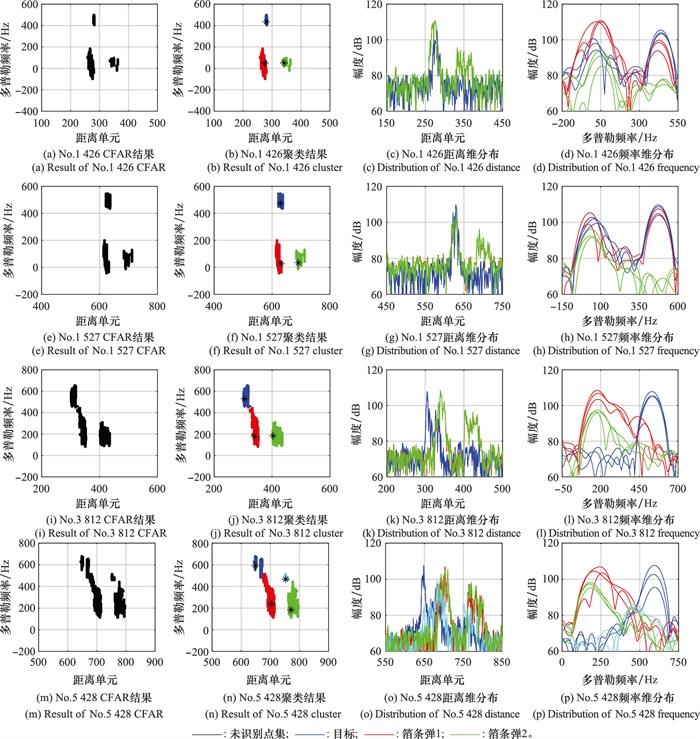
图8
第2发箔条弹的扩散过程
Fig.8
Diffusion process of the second chaff projectile
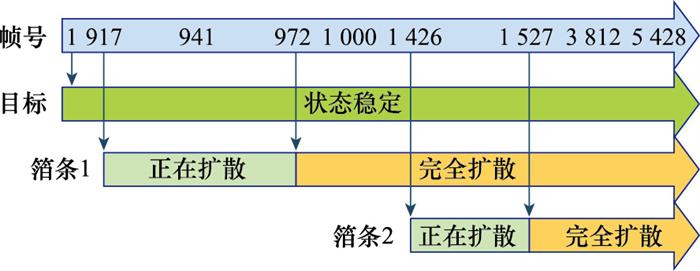
观察图 7 中的距离维分布, 箔条弹1从第917帧打出直至第1 527帧, 箔条弹1和目标在距离维是不可分辨的。由于目标速度与箔条速度存在明显差异, 第3 812帧时箔条弹1和目标在距离维度上分离开形成两个峰值。观察图 8 中的频率分布, 完全扩散后的箔条弹1峰值点周围距离单元的能量中心开始对齐, 谱宽稳定, 但能量仍不集中; 箔条弹2的扩散(第1 426帧、第1 527帧)与图 7 中箔条弹1扩散过程的结论相似: 峰值点周围单元频率分布中心不够集中, 且谱宽波动起伏较大; 箔条弹2完全扩散后(第3 812帧、第5 428帧)同样形成了能量中心对齐、谱宽稳定的趋势。在箔条弹2打出后, 目标峰值点周围距离单元的频率分布依旧保持着能量中心对齐且谱宽稳定的状态, 且相较于稳定后的箔条弹的频率分布, 目标的频率分布关于峰点对称分布, 能量更加集中。
图9
箔条弹扩散状态
Fig.9
Diffusion state of chaff projectile
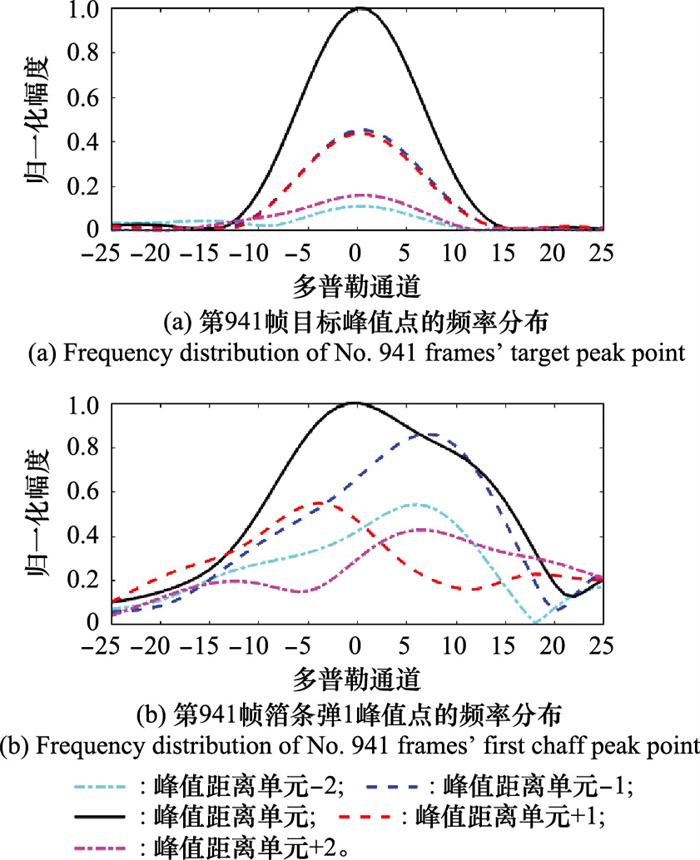
图10
第941帧频率分布
Fig.10
Frequency distribution of No.941 frames
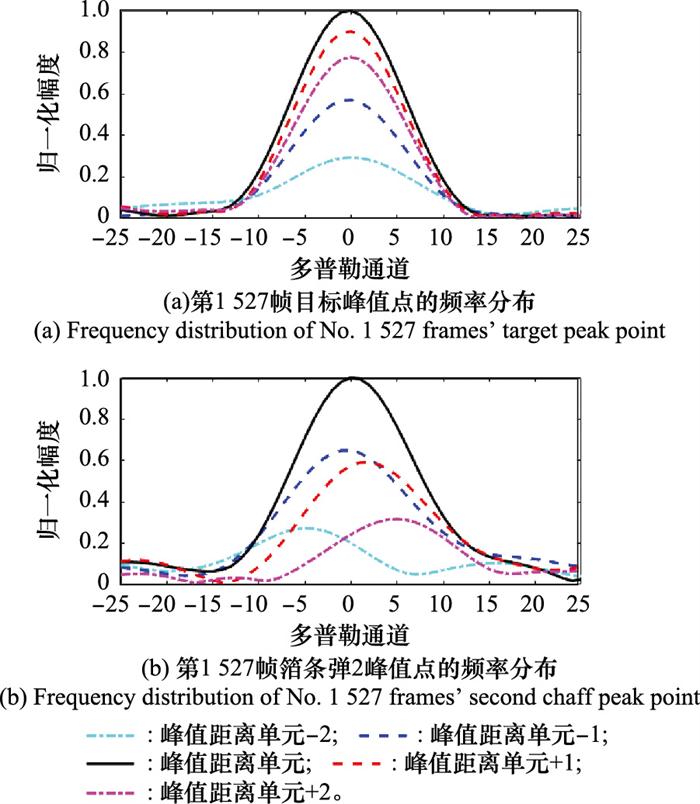
图11
第1 527帧频率分布
Fig.11
Frequency distribution of No.1 527 frames
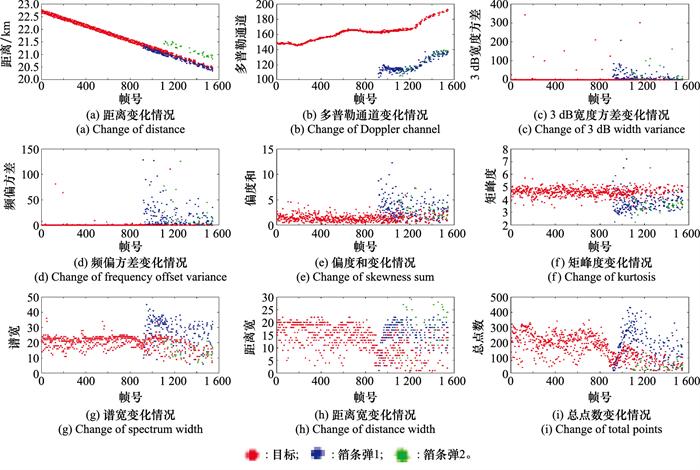
图12
特征统计分析
Fig.12
Analysis of feature statistics
如表 4 所示, 3个分类器均能够不同程度地完成箔条的识别任务。其中, 最主要的分类错误来源于箔条1和箔条2之间的混淆。在实际应用中,该类错误不影响目标识别。括号内的数字表示不忽略箔条1、箔条2混淆错误的准确率, 括号外的数字表示忽略该错误的准确率。显然, 就准确率而言,随机森林>支持向量机>朴素贝叶斯; 但是,朴素贝叶斯却具备最短的训练时间和最快的预测速度; 随机森林虽然准确率高, 但预测速度异常慢。这是由分类器模型的复杂度导致的。对于末制导雷达而言, 预测速度关乎雷达能否及时辨别目标, 准确度体现了分类性能。在能够进行离线训练的条件下,训练时间并不重要, 只有在线学习的条件下才有必要考虑训练时间。因此, 在允许离线训练的条件下, 相较于另外两种分类器, 支持向量机既有较高的准确率, 也有了较快的预测速度。
[1]
尚炜 , 陈伯孝 , 蒋丽凤 . 基于频谱展宽效应的一种抗箔条方法
[J]. 制导与引信 , 2006 , 27 (3 ): 5-9, 24
[本文引用: 1]
SHANG W , CHEN B X , JIANG L F . An anti-chaff jamming method based on the effect of spectral expansion
[J]. Guidance & Fuze , 2006 , 27 (3 ): 5-9, 24
[本文引用: 1]
[2]
陈静 . 雷达箔条干扰原理 [M]. 北京 : 国防工业出版社 , 2007 .
[本文引用: 2]
CHEN J . Principles of radar chaff jamming [M]. Beijing : National Defense Industry Publishing House , 2007 .
[本文引用: 2]
[3]
李伟 , 贾惠波 , 顾启泰 . 识别箔条干扰的一种实用方法
[J]. 现代雷达 , 2000 , 22 (3 ): 37 - 40 .
[本文引用: 1]
LI W , JIA H B , GU Q T . A practical method against chaff jamming for the radar
[J]. Modern Radar , 2000 , 22 (3 ): 37 - 40 .
[本文引用: 1]
[4]
ZAK J, VACH M, DVORACEK F. Advanced chaff usage in modern EW[C]//Proc. of the IEEE Radar Methods and Systems Workshop, 2016: 56-59.
[本文引用: 1]
[5]
GILLES R . Chaff and flare overview [M]. London : BAE Systems , 2010 .
[本文引用: 1]
[6]
ZHU G Q, MAN L, CHEN Y, et al. Approach of electromagnetic modeling for chaff clouds formed by exploding[C]//Proc. of the IEEE International Conference on Computational Electromagnetics, 2018.
[本文引用: 1]
[7]
ZAK J, GREGOR L, DVORACEK F, et al. Measurement of CHAFF RCS[C]//Proc. of the IEEE 19th International Radar Symposium, 2018: 1-7.
[8]
ZUO Y C, GUO L X, XIAO D H. The near-field scattering of chaff cloud[C]//Proc. of the IEEE Cross Strait Quad-Regional Radio Science and Wireless Technology Conference, 2018.
[9]
马贤杰 , 马榜 , 李石川 , 等 . 直升机载箔条弹干扰效能分析
[J]. 航天电子对抗 , 2018 , 34 (6 ): 17 - 22 .
[本文引用: 1]
MA X J , MA B , LI S C , et al . Analysis of interference effectiveness of helicopter-borne chaff bombs
[J]. Aerospace Electronic Warfare , 2018 , 34 (6 ): 17 - 22 .
[本文引用: 1]
[10]
GUO L X, ZUO Y C. Investigation on the electromagnetic scattering from the chaff cloud in airflow with VRT[C]//Proc. of the IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization, 2020.
[本文引用: 1]
[11]
YIN C, BO Y. An improved model for computing the scattering amplitude coefficient of the chaff cloud[C]//Proc. of the IEEE Workshop on Advanced Research and Technology in Industry Applications, 2014: 1371-1374.
[12]
ZHOU Z Y, LI J L, LIANG X X, et al. Polarization and frequency spectra characteristics of chaff cloud clutter signals[C]// Proc. of the IEEE International Conference on Computational Electromagnetics, 2019.
[13]
ZHANG L, WU Z. Simulation of full-polarization electromagnetic back-scattering characteristics of large number of high-density chaff clouds[C]//Proc. of the IEEE Cross Strait Quad-Regional Radio Science and Wireless Technology Conference, 2019.
[14]
CUI G, SHI L F, MA J, et al. Study on chaff diffusion and polarization stratification[C]//Proc. of the IEEE International Conference on Computational Electromagnetics, 2018.
[15]
全斯农 , 范晖 , 代大海 , 等 . 一种基于精细极化目标分解的舰船箔条云识别方法
[J]. 雷达学报 , 2021 , 10 (1 ): 61 .
QUAN S N , FAN H , DAI D H , et al . Recognition of ships and chaff clouds based on sophisticated polarimetric target decomposition
[J]. Journal of Radars , 2021 , 10 (1 ): 61 .
[17]
李永祯 , 刘业民 , 庞晨 , 等 . 基于分层极化特性的箔条云识别方法研究
[J]. 系统工程与电子技术 , 2021 , 43 (8 ): 2099 - 2107 .
LI Y Z , LIU Y M , PANG C . Study on chaff clouds recognition method based on layered polarization characteristics
[J]. Systems Engineering and Electronics , 2021 , 43 (8 ): 2099 - 2107 .
[18]
LEE H, KIM S. Fuzzy decision tree based Gentle Boost algorithm for detecting chaff echo in weather radar data[C]//Proc. of the IEEE 7th Joint International Conference on Soft Computing and Intelligent Systems and 15th International Symposium on Advanced Intelligent Systems, 2014: 1443-1448.
[本文引用: 1]
[19]
ZHANG L F, ZHEN S. Dynamic diffusion modeling and scattering characteristic of large number chaff clouds[C]//Proc. of the IEEE International Symposium on Antennas and Propagation, 2019.
[本文引用: 1]
[20]
LI R, HAO X, BAI S. The micro-Doppler features extraction of experimental data of chaff cloud scatter dispersion based on empirical mode decomposition[C]//Proc. of the IEEE International Conference on Signal, Information and Data Processing, 2019.
[本文引用: 1]
[21]
赵海波 , 胡光锐 . 基于自适应联合时频处理的抗箔条干扰技术
[J]. 上海交通大学学报 , 2008 , 42 (7 ): 1211 - 1216 .
ZHAO H B , HU G R . Anti-cloud jamming method based on adaptive joint time-frequency processing
[J]. Journal of Shanghai Jiaotong University , 2008 , 42 (7 ): 1211 - 1216 .
[22]
舒欣 , 沈福民 . 时频分析技术在抑制箔条干扰中的应用
[J]. 西安电子科技大学学报 , 2001 , 28 (5 ): 676 - 680 .
[本文引用: 1]
SHU X , SHEN F M . The application of the time-frequency analysis
[J]. Journal of Xidian University , 2001 , 28 (5 ): 676 - 680 .
[本文引用: 1]
[23]
LIU Y M , XING S Q , LIU Y C , et al . Maximum likelihood angle estimation of target in the presence of chaff centroid jamming
[J]. IEEE Access , 2018 , 6 , 74416 - 74428 .
[本文引用: 1]
[24]
刘业民 , 邢世其 , 李永祯 , 等 . 基于极化单脉冲雷达的角度估计方法
[J]. 系统工程与电子技术 , 2018 , 40 (8 ): 50 - 56 .
[本文引用: 1]
LIU Y M , XING S Q , LI Y Z , et al . Method for angle estimating based on polarization monopulse radar
[J]. Systems Engineering and Electronics , 2018 , 40 (8 ): 50 - 56 .
[本文引用: 1]
[25]
李金梁 , 来庆福 , 李永祯 , 等 . 基于极化对比增强的导引头抗箔条算法
[J]. 系统工程与电子技术 , 2011 , 33 (2 ): 268 - 271 .
[本文引用: 1]
LI J L , LAI Q F , LI Y Z , et al . Anti-chaff algorithm for seekers based on polarimetric contrast enhancement
[J]. Systems Engineering and Electronics , 2011 , 33 (2 ): 268 - 271 .
[本文引用: 1]
[26]
ZUO Y C, GUO L X, LIU W. A scattering evaluation method of chaff cloud based on VRT and SVM[C]//Proc. of the IEEE Photonics & Electromagnetics Research Symposium-Fall, 2019: 1105-1108.
[本文引用: 2]
[27]
KAYDOK U. Chaff discrimination using convolutional neural networks and range profile data[C]//Proc. of the IEEE International Radar Conference, 2020: 373-377.
[本文引用: 1]
[28]
刘世敏. 箔条干扰的特征及其实测数据分析[D]. 西安: 西安电子科技大学, 2009: 23-44.
[本文引用: 3]
LIU S M. Characteristics of chaff interference and analysis of actual data[D]. Xi'an: Xidian University, 2009: 23-44.
[本文引用: 3]
[29]
刘博 , 常文革 . 反舰宽带相参雷达的一种抗箔条干扰方法
[J]. 系统工程与电子技术 , 2014 , 34 (3 ): 38 - 44 .
URL
LIU B , CHANG W G . Effective anti-chaff jamming method for anti-ship wideband coherent radar
[J]. Systems Engineering and Electronics , 2014 , 34 (3 ): 38 - 44 .
URL
[30]
曹司磊 , 曾维贵 , 刘明刚 . 基于区域判别的抗质心式箔条干扰方法
[J]. 兵工自动化 , 2017 , (6 ): 70 - 74 .
[本文引用: 4]
CAO S L , ZENG W G , LIU M G . Centroid-chaff jamming confrontation based on region discrimination
[J]. Ordnance Industry Automation , 2017 , (6 ): 70 - 74 .
[本文引用: 4]
[31]
陈伯孝 . 现代雷达系统分析与设计 [M]. 西安 : 西安电子科技大学出版社 , 2012 .
[本文引用: 1]
CHEN B X . Modern radar system analysis and design [M]. Xi'an : Xidian University Press , 2012 .
[本文引用: 1]
[32]
WINKLER V. Range Doppler detection for automotive FMCW radars[C]//Proc. of the IEEE European Radar Conference, 2007: 166-169.
[本文引用: 1]
[33]
FUKUNAGA K , HOSTETLER L D . The estimation of the gradient of a density function, with applications in pattern recognition
[J]. IEEE Trans.on Information , 1975 , 21 (1 ): 32 - 40 .
[本文引用: 1]
[34]
CHENG Y Z . Mean shift, mode seeking, and clustering
[J]. IEEE Trans.on Pattern Analysis and Machine Intelligence , 1995 , 17 (8 ): 790 - 799 .
[本文引用: 1]
[35]
周芳芳 , 樊晓平 , 叶榛 . 均值漂移算法的研究与应用
[J]. 控制与决策 , 2007 , 22 (8 ): 841 - 847 .
[本文引用: 1]
ZHOU F F , FAN X P , YE Z . Mean shift research and applications
[J]. Control and Decision , 2007 , 22 (8 ): 841 - 847 .
[本文引用: 1]
[36]
JOANES D N , GILL C A . Comparing measures of sample skewness and kurtosis
[J]. Journal of the Royal Statistical Society , 2010 , 47 (1 ): 183 - 189 .
[本文引用: 2]
基于频谱展宽效应的一种抗箔条方法
1
2006
... 箔条干扰作为一种常见的雷达无源干扰手段, 在1973年海战中被首次投入使用, 由于其具备干扰效果显著、干扰实施便捷和干扰成本低廉的优势, 现已被广泛应用于电子对抗(electronic countermeasures, ECM)[1 ] .箔条弹打出后抛撒在空中,通过扩散形成具有一定长度、宽度和厚度的云状干扰物, 称为箔条走廊[2 ] .箔条本身没有动力, 完全依靠自然扩散, 以箔条走廊尺寸、谱宽的稳定性为依据, 将扩散过程分为正在扩散状态和完全扩散状态[3 ] .以箔条弹打出位置是否与目标在同一波束内为依据,分为质心式和冲淡式, 质心式箔条干扰可以近距离利用箔条走廊遮盖并保护目标; 冲淡式干扰的箔条走廊可以在远距离处形成诱饵[4 -5 ] .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
An anti-chaff jamming method based on the effect of spectral expansion
1
2006
... 箔条干扰作为一种常见的雷达无源干扰手段, 在1973年海战中被首次投入使用, 由于其具备干扰效果显著、干扰实施便捷和干扰成本低廉的优势, 现已被广泛应用于电子对抗(electronic countermeasures, ECM)[1 ] .箔条弹打出后抛撒在空中,通过扩散形成具有一定长度、宽度和厚度的云状干扰物, 称为箔条走廊[2 ] .箔条本身没有动力, 完全依靠自然扩散, 以箔条走廊尺寸、谱宽的稳定性为依据, 将扩散过程分为正在扩散状态和完全扩散状态[3 ] .以箔条弹打出位置是否与目标在同一波束内为依据,分为质心式和冲淡式, 质心式箔条干扰可以近距离利用箔条走廊遮盖并保护目标; 冲淡式干扰的箔条走廊可以在远距离处形成诱饵[4 -5 ] .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
2
2007
... 箔条干扰作为一种常见的雷达无源干扰手段, 在1973年海战中被首次投入使用, 由于其具备干扰效果显著、干扰实施便捷和干扰成本低廉的优势, 现已被广泛应用于电子对抗(electronic countermeasures, ECM)[1 ] .箔条弹打出后抛撒在空中,通过扩散形成具有一定长度、宽度和厚度的云状干扰物, 称为箔条走廊[2 ] .箔条本身没有动力, 完全依靠自然扩散, 以箔条走廊尺寸、谱宽的稳定性为依据, 将扩散过程分为正在扩散状态和完全扩散状态[3 ] .以箔条弹打出位置是否与目标在同一波束内为依据,分为质心式和冲淡式, 质心式箔条干扰可以近距离利用箔条走廊遮盖并保护目标; 冲淡式干扰的箔条走廊可以在远距离处形成诱饵[4 -5 ] .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
... .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
2
2007
... 箔条干扰作为一种常见的雷达无源干扰手段, 在1973年海战中被首次投入使用, 由于其具备干扰效果显著、干扰实施便捷和干扰成本低廉的优势, 现已被广泛应用于电子对抗(electronic countermeasures, ECM)[1 ] .箔条弹打出后抛撒在空中,通过扩散形成具有一定长度、宽度和厚度的云状干扰物, 称为箔条走廊[2 ] .箔条本身没有动力, 完全依靠自然扩散, 以箔条走廊尺寸、谱宽的稳定性为依据, 将扩散过程分为正在扩散状态和完全扩散状态[3 ] .以箔条弹打出位置是否与目标在同一波束内为依据,分为质心式和冲淡式, 质心式箔条干扰可以近距离利用箔条走廊遮盖并保护目标; 冲淡式干扰的箔条走廊可以在远距离处形成诱饵[4 -5 ] .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
... .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
识别箔条干扰的一种实用方法
1
2000
... 箔条干扰作为一种常见的雷达无源干扰手段, 在1973年海战中被首次投入使用, 由于其具备干扰效果显著、干扰实施便捷和干扰成本低廉的优势, 现已被广泛应用于电子对抗(electronic countermeasures, ECM)[1 ] .箔条弹打出后抛撒在空中,通过扩散形成具有一定长度、宽度和厚度的云状干扰物, 称为箔条走廊[2 ] .箔条本身没有动力, 完全依靠自然扩散, 以箔条走廊尺寸、谱宽的稳定性为依据, 将扩散过程分为正在扩散状态和完全扩散状态[3 ] .以箔条弹打出位置是否与目标在同一波束内为依据,分为质心式和冲淡式, 质心式箔条干扰可以近距离利用箔条走廊遮盖并保护目标; 冲淡式干扰的箔条走廊可以在远距离处形成诱饵[4 -5 ] .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
A practical method against chaff jamming for the radar
1
2000
... 箔条干扰作为一种常见的雷达无源干扰手段, 在1973年海战中被首次投入使用, 由于其具备干扰效果显著、干扰实施便捷和干扰成本低廉的优势, 现已被广泛应用于电子对抗(electronic countermeasures, ECM)[1 ] .箔条弹打出后抛撒在空中,通过扩散形成具有一定长度、宽度和厚度的云状干扰物, 称为箔条走廊[2 ] .箔条本身没有动力, 完全依靠自然扩散, 以箔条走廊尺寸、谱宽的稳定性为依据, 将扩散过程分为正在扩散状态和完全扩散状态[3 ] .以箔条弹打出位置是否与目标在同一波束内为依据,分为质心式和冲淡式, 质心式箔条干扰可以近距离利用箔条走廊遮盖并保护目标; 冲淡式干扰的箔条走廊可以在远距离处形成诱饵[4 -5 ] .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
1
... 箔条干扰作为一种常见的雷达无源干扰手段, 在1973年海战中被首次投入使用, 由于其具备干扰效果显著、干扰实施便捷和干扰成本低廉的优势, 现已被广泛应用于电子对抗(electronic countermeasures, ECM)[1 ] .箔条弹打出后抛撒在空中,通过扩散形成具有一定长度、宽度和厚度的云状干扰物, 称为箔条走廊[2 ] .箔条本身没有动力, 完全依靠自然扩散, 以箔条走廊尺寸、谱宽的稳定性为依据, 将扩散过程分为正在扩散状态和完全扩散状态[3 ] .以箔条弹打出位置是否与目标在同一波束内为依据,分为质心式和冲淡式, 质心式箔条干扰可以近距离利用箔条走廊遮盖并保护目标; 冲淡式干扰的箔条走廊可以在远距离处形成诱饵[4 -5 ] .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
1
2010
... 箔条干扰作为一种常见的雷达无源干扰手段, 在1973年海战中被首次投入使用, 由于其具备干扰效果显著、干扰实施便捷和干扰成本低廉的优势, 现已被广泛应用于电子对抗(electronic countermeasures, ECM)[1 ] .箔条弹打出后抛撒在空中,通过扩散形成具有一定长度、宽度和厚度的云状干扰物, 称为箔条走廊[2 ] .箔条本身没有动力, 完全依靠自然扩散, 以箔条走廊尺寸、谱宽的稳定性为依据, 将扩散过程分为正在扩散状态和完全扩散状态[3 ] .以箔条弹打出位置是否与目标在同一波束内为依据,分为质心式和冲淡式, 质心式箔条干扰可以近距离利用箔条走廊遮盖并保护目标; 冲淡式干扰的箔条走廊可以在远距离处形成诱饵[4 -5 ] .文献[2 ]已证明,箔条走廊的干扰功能与雷达体制无关, 对于现有的脉冲多普勒雷达、相控阵雷达、合成孔径雷达、毫米波雷达及未来的新体制雷达而言, 箔条干扰都将是一种有效的干扰手段, 因此无论是现在还是将来,研究抗箔条干扰问题都是非常有意义的. ...
1
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
直升机载箔条弹干扰效能分析
1
2018
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
Analysis of interference effectiveness of helicopter-borne chaff bombs
1
2018
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
1
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
一种基于精细极化目标分解的舰船箔条云识别方法
0
2021
Recognition of ships and chaff clouds based on sophisticated polarimetric target decomposition
0
2021
关于制导雷达目标识别抗箔条干扰仿真研究
0
2016
Anti-chaff jamming method of target recognition for guidance radar based on frequency characteristics
0
2016
基于分层极化特性的箔条云识别方法研究
0
2021
Study on chaff clouds recognition method based on layered polarization characteristics
0
2021
1
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
1
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
1
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
基于自适应联合时频处理的抗箔条干扰技术
0
2008
Anti-cloud jamming method based on adaptive joint time-frequency processing
0
2008
时频分析技术在抑制箔条干扰中的应用
1
2001
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
The application of the time-frequency analysis
1
2001
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
Maximum likelihood angle estimation of target in the presence of chaff centroid jamming
1
2018
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
基于极化单脉冲雷达的角度估计方法
1
2018
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
Method for angle estimating based on polarization monopulse radar
1
2018
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
基于极化对比增强的导引头抗箔条算法
1
2011
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
Anti-chaff algorithm for seekers based on polarimetric contrast enhancement
1
2011
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
2
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
... 本文将在R-D图上寻找目标、箔条的特征信息, 并借鉴了引言中第3种思路的研究成果.文献[27 ]采用卷积神经网络的方式对目标、箔条峰值点的距离分布数据进行训练、学习、分类识别; 文献[28 -30 ]则分别对目标、箔条的距离和频率分布特征进行了讨论研究.上述文献只考虑了识别, 并未考虑分离, 即只有在尚未识别目标、箔条的条件下, 在R-D图中将目标与箔条进行分离才能进行识别.文献[26 ]通过边界搜索的方式先分离目标与箔条, 再进行识别.但是箔条云本身存在距离、多普勒维度的扩展, 边界搜索并不能够准确分离目标与箔条. ...
1
... 本文将在R-D图上寻找目标、箔条的特征信息, 并借鉴了引言中第3种思路的研究成果.文献[27 ]采用卷积神经网络的方式对目标、箔条峰值点的距离分布数据进行训练、学习、分类识别; 文献[28 -30 ]则分别对目标、箔条的距离和频率分布特征进行了讨论研究.上述文献只考虑了识别, 并未考虑分离, 即只有在尚未识别目标、箔条的条件下, 在R-D图中将目标与箔条进行分离才能进行识别.文献[26 ]通过边界搜索的方式先分离目标与箔条, 再进行识别.但是箔条云本身存在距离、多普勒维度的扩展, 边界搜索并不能够准确分离目标与箔条. ...
3
... 本文将在R-D图上寻找目标、箔条的特征信息, 并借鉴了引言中第3种思路的研究成果.文献[27 ]采用卷积神经网络的方式对目标、箔条峰值点的距离分布数据进行训练、学习、分类识别; 文献[28 -30 ]则分别对目标、箔条的距离和频率分布特征进行了讨论研究.上述文献只考虑了识别, 并未考虑分离, 即只有在尚未识别目标、箔条的条件下, 在R-D图中将目标与箔条进行分离才能进行识别.文献[26 ]通过边界搜索的方式先分离目标与箔条, 再进行识别.但是箔条云本身存在距离、多普勒维度的扩展, 边界搜索并不能够准确分离目标与箔条. ...
... 如图 3 所示,MS算法准确地凝聚了2D-CFAR结果, 每种颜色表示一类, 并标记了各类密度中心点.在此基础上,可以采取文献[28 -30 ]的方式, 利用各点集所占据的多普勒通道数(谱宽)、距离单元数识别箔条. ...
... 在实际场景中, 目标为多点模型, 箔条为箔条云团模型.本文以文献[28 -30 ]分析峰值距离单元的频率分布为基础, 兼顾峰值相邻距离单元的频率分布, 并提出了新的特征信息辅助判别. ...
3
... 本文将在R-D图上寻找目标、箔条的特征信息, 并借鉴了引言中第3种思路的研究成果.文献[27 ]采用卷积神经网络的方式对目标、箔条峰值点的距离分布数据进行训练、学习、分类识别; 文献[28 -30 ]则分别对目标、箔条的距离和频率分布特征进行了讨论研究.上述文献只考虑了识别, 并未考虑分离, 即只有在尚未识别目标、箔条的条件下, 在R-D图中将目标与箔条进行分离才能进行识别.文献[26 ]通过边界搜索的方式先分离目标与箔条, 再进行识别.但是箔条云本身存在距离、多普勒维度的扩展, 边界搜索并不能够准确分离目标与箔条. ...
... 如图 3 所示,MS算法准确地凝聚了2D-CFAR结果, 每种颜色表示一类, 并标记了各类密度中心点.在此基础上,可以采取文献[28 -30 ]的方式, 利用各点集所占据的多普勒通道数(谱宽)、距离单元数识别箔条. ...
... 在实际场景中, 目标为多点模型, 箔条为箔条云团模型.本文以文献[28 -30 ]分析峰值距离单元的频率分布为基础, 兼顾峰值相邻距离单元的频率分布, 并提出了新的特征信息辅助判别. ...
反舰宽带相参雷达的一种抗箔条干扰方法
0
2014
Effective anti-chaff jamming method for anti-ship wideband coherent radar
0
2014
基于区域判别的抗质心式箔条干扰方法
4
2017
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
... 本文将在R-D图上寻找目标、箔条的特征信息, 并借鉴了引言中第3种思路的研究成果.文献[27 ]采用卷积神经网络的方式对目标、箔条峰值点的距离分布数据进行训练、学习、分类识别; 文献[28 -30 ]则分别对目标、箔条的距离和频率分布特征进行了讨论研究.上述文献只考虑了识别, 并未考虑分离, 即只有在尚未识别目标、箔条的条件下, 在R-D图中将目标与箔条进行分离才能进行识别.文献[26 ]通过边界搜索的方式先分离目标与箔条, 再进行识别.但是箔条云本身存在距离、多普勒维度的扩展, 边界搜索并不能够准确分离目标与箔条. ...
... 如图 3 所示,MS算法准确地凝聚了2D-CFAR结果, 每种颜色表示一类, 并标记了各类密度中心点.在此基础上,可以采取文献[28 -30 ]的方式, 利用各点集所占据的多普勒通道数(谱宽)、距离单元数识别箔条. ...
... 在实际场景中, 目标为多点模型, 箔条为箔条云团模型.本文以文献[28 -30 ]分析峰值距离单元的频率分布为基础, 兼顾峰值相邻距离单元的频率分布, 并提出了新的特征信息辅助判别. ...
Centroid-chaff jamming confrontation based on region discrimination
4
2017
... 针对如何对抗箔条干扰的问题, 目前已有许多学者给出了解决方案, 梳理参考文献,大致总结出如下3种思路: 第1种是以箔条自身物理特征建模为基础, 研究其雷达反射截面积特性[6 -9 ] 、极化散射特性[10 -18 ] 和扩散模型等物理特征[19 ] 与目标的差异, 实现目标与箔条走廊的识别; 第2种是对回波信号进行预处理, 采用时频分析的方式提取时频特征完成目标回波的分离[20 -22 ] , 或者采用角度估计优化算法[23 -24 ] 、极化增强目标信号等方式抑制干扰信号[25 ] ; 第3种是从常规雷达信号处理后的距离-多普勒(range-Doppler, R-D)二维图出发, 分析R-D图中目标、箔条占据的距离单元数和多普勒通道数(谱宽), 将目标与箔条区分开[26 -30 ] .第1种思路能够实现非常高的识别准确率, 但由于箔条金属自身尺寸、镀层和极化散射特性等工艺指标并不统一, 抗干扰方更无法获知此类关键信息, 故这类方法实用性不强; 第2种思路能够有效地对抗状态稳定的箔条干扰, 但由于从未扩散到完全扩散整个过程的回波特性并不稳定, 所以这类方法不能稳定、有效地对抗整个扩散过程的箔条干扰; 第3种思路同样能够在完全扩散状态下准确地分辨目标与箔条, 但需要根据扩散过程调整判决门限, 且无法区分未扩散状态的箔条假目标. ...
... 本文将在R-D图上寻找目标、箔条的特征信息, 并借鉴了引言中第3种思路的研究成果.文献[27 ]采用卷积神经网络的方式对目标、箔条峰值点的距离分布数据进行训练、学习、分类识别; 文献[28 -30 ]则分别对目标、箔条的距离和频率分布特征进行了讨论研究.上述文献只考虑了识别, 并未考虑分离, 即只有在尚未识别目标、箔条的条件下, 在R-D图中将目标与箔条进行分离才能进行识别.文献[26 ]通过边界搜索的方式先分离目标与箔条, 再进行识别.但是箔条云本身存在距离、多普勒维度的扩展, 边界搜索并不能够准确分离目标与箔条. ...
... 如图 3 所示,MS算法准确地凝聚了2D-CFAR结果, 每种颜色表示一类, 并标记了各类密度中心点.在此基础上,可以采取文献[28 -30 ]的方式, 利用各点集所占据的多普勒通道数(谱宽)、距离单元数识别箔条. ...
... 在实际场景中, 目标为多点模型, 箔条为箔条云团模型.本文以文献[28 -30 ]分析峰值距离单元的频率分布为基础, 兼顾峰值相邻距离单元的频率分布, 并提出了新的特征信息辅助判别. ...
1
2012
... 式中: sinc(u )=sin u /u .单点目标和箔条丝会在t =τ +n Tr +fd /μ 处形成一个sinc函数形状的峰值[31 ] . ...
1
2012
... 式中: sinc(u )=sin u /u .单点目标和箔条丝会在t =τ +n Tr +fd /μ 处形成一个sinc函数形状的峰值[31 ] . ...
1
... 箔条云团存在两个维度同时展宽的现象, 在两个维度同时进行CFAR(two-dimensional CFAR, 2D-CFAR)[32 ] 处理的结果将比单一维度的CFAR更为可靠. ...
The estimation of the gradient of a density function, with applications in pattern recognition
1
1975
... 均值漂移(mean shift, MS)算法是一种有效的统计迭代算法[33 ] , 1995年,Cheng[34 ] 将其改进后应用于聚类和全局优化, 此后该算法在计算机视觉领域得到了广泛应用.MS算法的基本思想是, 通过反复迭代搜索特征空间中样本点最密集的区域[35 ] , 即按照分布密度进行聚类.MS算法具备原理简单、迭代效率高、聚类准确的特点, 非常适合被应用于凝聚2D-CFAR后的目标、箔条点集. ...
Mean shift, mode seeking, and clustering
1
1995
... 均值漂移(mean shift, MS)算法是一种有效的统计迭代算法[33 ] , 1995年,Cheng[34 ] 将其改进后应用于聚类和全局优化, 此后该算法在计算机视觉领域得到了广泛应用.MS算法的基本思想是, 通过反复迭代搜索特征空间中样本点最密集的区域[35 ] , 即按照分布密度进行聚类.MS算法具备原理简单、迭代效率高、聚类准确的特点, 非常适合被应用于凝聚2D-CFAR后的目标、箔条点集. ...
均值漂移算法的研究与应用
1
2007
... 均值漂移(mean shift, MS)算法是一种有效的统计迭代算法[33 ] , 1995年,Cheng[34 ] 将其改进后应用于聚类和全局优化, 此后该算法在计算机视觉领域得到了广泛应用.MS算法的基本思想是, 通过反复迭代搜索特征空间中样本点最密集的区域[35 ] , 即按照分布密度进行聚类.MS算法具备原理简单、迭代效率高、聚类准确的特点, 非常适合被应用于凝聚2D-CFAR后的目标、箔条点集. ...
Mean shift research and applications
1
2007
... 均值漂移(mean shift, MS)算法是一种有效的统计迭代算法[33 ] , 1995年,Cheng[34 ] 将其改进后应用于聚类和全局优化, 此后该算法在计算机视觉领域得到了广泛应用.MS算法的基本思想是, 通过反复迭代搜索特征空间中样本点最密集的区域[35 ] , 即按照分布密度进行聚类.MS算法具备原理简单、迭代效率高、聚类准确的特点, 非常适合被应用于凝聚2D-CFAR后的目标、箔条点集. ...
Comparing measures of sample skewness and kurtosis
2
2010
... 矩峰度与偏度通常在统计学中用于描述分布的形状特征, 矩峰度表征了概率密度分布曲线在均值处的尖锐程度; 偏度度量了样本分布的偏斜程度及偏向[36 ] . ...
... 文献[36 ]中,关于样本X 的矩峰度K urtosis 、偏度S kewness 定义如下: ...