[1]
ROSENBLATT F . The perceptron: a probabilistic model for information storage and organization in the brain
[J]. Psychological Review , 1958 , 65 (6 ): 386 .
DOI:10.1037/h0042519
[本文引用: 2]
[2]
RUMELHART D E , MCCLELLAND J L . Parallel distributed processing: explorations in the microstructure of cognition [M]. Cambridge : MIT Press , 1986 .
[本文引用: 1]
[3]
ANDERSON J A . A simple neural network generating an inte-ractive memory
[J]. Mathematical Biosciences , 1972 , 14 (3/4 ): 197 - 220 .
[本文引用: 2]
[4]
KOHONEN T . Correlation matrix memories
[J]. IEEE Trans.on Computers , 1972 , 100 (4 ): 353 - 359 .
[本文引用: 2]
[5]
FUKUSHIMA K . Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position
[J]. Biological Cybernetics , 1980 , 36 , 193 - 202 .
DOI:10.1007/BF00344251
[本文引用: 2]
[6]
OLSHAUSEN B A , FIELD D J . Emergence of simple-cell receptive field properties by learning a sparse code for natural images
[J]. Nature , 1996 , 381 (6583 ): 607 - 609 .
DOI:10.1038/381607a0
[本文引用: 1]
[7]
BELL A J , SEJNOWSKI T J . An information-maximization approach to blind separation and blind deconvolution
[J]. Neural Computation , 1995 , 7 (6 ): 1129 - 1159 .
DOI:10.1162/neco.1995.7.6.1129
[本文引用: 1]
[8]
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]//Proc. of the Conference on Advances in Neural Information Processing Systems, 2012, 25: 1097-1105.
[本文引用: 1]
[9]
HE K M, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//Proc. of the IEEE Conference on Computer Vision and Pattern Recognition, 2016: 770-778.
[本文引用: 1]
[10]
SUTSKEVER I, VINYALS O, LE Q V. Sequence to sequence learning with neural networks[C]//Proc. of the Conference on Advances in Neural Information Processing Systems, 2014: 3104-3112.
[本文引用: 1]
[11]
HINTON G E , DENG L , YU D , et al . Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups
[J]. IEEE Signal Processing Magazine , 2012 , 29 (6 ): 82 - 97 .
DOI:10.1109/MSP.2012.2205597
[本文引用: 1]
[12]
LI F F , FERGUS R , PERONA P . One-shot learning of object categories
[J]. IEEE Trans.on Pattern Analysis and Machine Intelligence , 2006 , 28 (4 ): 594 - 611 .
DOI:10.1109/TPAMI.2006.79
[本文引用: 1]
[13]
LIU Z, LI J G, SHEN Z Q, et al. Learning efficient convolutional networks through network slimming[C]//Proc. of the IEEE International Conference on Computer Vision, 2017: 2736-2744.
[本文引用: 1]
[14]
ZEILER M D, FERGUS R. Visualizing and understanding convolutional networks[C]//Proc. of the European Conference on Computer Vision, 2014: 818-833.
[本文引用: 1]
[15]
ZHANG Y , TINˇO P , LEONARDIS A , et al . A survey on neural network interpretability
[J]. IEEE Trans.on Emerging Topics in Computational Intelligence , 2021 , 5 (5 ): 726 - 742 .
DOI:10.1109/TETCI.2021.3100641
[本文引用: 1]
[16]
THOMAS A , DASGUPTA S , ROSING T . Theoretical foundations of hyperdimensional computing
[J]. Journal of Artificial Intelligence Research , 2021 , 72 , 215 - 249 .
DOI:10.1613/jair.1.12664
[本文引用: 3]
[17]
KANERVA P . Sparse distributed memory [M]. Cambridge : MIT Press , 1988 .
[本文引用: 3]
[18]
KANERVA P . Hyperdimensional computing: an introduction to computing in distributed representation with high-dimensional random vectors
[J]. Cognitive Computation , 2009 , 1 (2 ): 139 - 159 .
DOI:10.1007/s12559-009-9009-8
[本文引用: 5]
[19]
MASSE N Y , TURNER G C , JEFFERIS G S X E . Olfactory information processing in Drosophila
[J]. Current Biology , 2009 , 19 (16 ): R700 - R713 .
DOI:10.1016/j.cub.2009.06.026
[本文引用: 1]
[20]
CARON S J C , RUTA V , ABBOTT L F , et al . Random convergence of olfactory inputs in the Drosophila mushroom body
[J]. Nature , 2013 , 497 (7447 ): 113 - 117 .
DOI:10.1038/nature12063
[本文引用: 1]
[21]
SQUIRE L R . Memory and the hippocampus: a synthesis from findings with rats, monkeys, and humans
[J]. Psychological Review , 1992 , 99 (2 ): 195 - 231 .
DOI:10.1037/0033-295X.99.2.195
[本文引用: 1]
[22]
RAHIMI A, KANERVA P, RABAEY J M. A robust and energy-efficient classifier using brain-inspired hyperdimensional computing[C]//Proc. of the International Symposium on Low Power Electronics and Design, 2016: 64-69.
[本文引用: 3]
[23]
ZHANG S, WANG R, ZHANG J J, et al. Assessing robustness of hyperdimensional computing against errors in associative memory[C]//Proc. of the IEEE 32nd International Conference on Application-specific Systems, Architectures and Processors, 2021: 211-217.
[24]
HERSCHE M , LIPPUNER S , KORB M , et al . Near-channel classifier: symbiotic communication and classification in high-dimensional space
[J]. Brain Informatics , 2021 , 8 (1 ): 16 .
DOI:10.1186/s40708-021-00138-0
[25]
KARUNARATNE G , SCHMUCK M , LE GALLO M , et al . Robust high-dimensional memory-augmented neural networks
[J]. Nature Communications , 2021 , 12 (1 ): 2468 .
DOI:10.1038/s41467-021-22364-0
[本文引用: 1]
[26]
YAO Y R , LIU W B , ZHANG G , et al . Radar-based human activity recognition using hyperdimensional computing
[J]. IEEE Trans.on Microwave Theory and Techniques , 2022 , 70 (3 ): 1605 - 1619 .
DOI:10.1109/TMTT.2021.3134992
[本文引用: 6]
[27]
GE L L , PARHI K K . Classification using hyperdimensional computing: a review
[J]. IEEE Circuits and Systems Magazine , 2020 , 20 (2 ): 30 - 47 .
DOI:10.1109/MCAS.2020.2988388
[本文引用: 4]
[28]
HASSAN E , HALAWANI Y , MOHAMMAD B , et al . Hyper-dimensional computing challenges and opportunities for AI applications
[J]. IEEE Access , 2021 , 10 , 97651 - 97664 .
[本文引用: 2]
[29]
IMANI M, KONG D, RAHIMI A, et al. VoiceHD: hyperdimensional computing for efficient speech recognition[C]//Proc. of the IEEE International Conference on Rebooting Computing, 2017.
[本文引用: 3]
[30]
JOSHI A, HALSETH J T, KANERVA P. Language geometry using random indexing[C]//Proc. of the International Symposium on Quantum Interaction, 2016: 265-274.
[本文引用: 2]
[31]
IMANI M , HWANG J , ROSING T , et al . Low-power sparse hyperdimensional encoder for language recognition
[J]. IEEE Design and Test , 2017 , 34 (6 ): 94 - 101 .
DOI:10.1109/MDAT.2017.2740839
[本文引用: 3]
[32]
MA D N, GUO J M, JIANG Y, et al. HDTest: differential fuzz testing of brain-inspired hyperdimensional computing[C]//Proc. of the ACM/IEEE Design Automation Conference, 2021: 391-396.
[本文引用: 2]
[33]
YAO Y R , LIU W B , ZHANG G , et al . Fast SAR image recog-nition via hyperdimensional computing using monogenic mapping
[J]. IEEE Geoscience and Remote Sensing Letters , 2022 , 19 , 4508205 .
[本文引用: 3]
[34]
RAHIMI A , KANERVA P , BENINI L , et al . Efficient biosignal processing using hyperdimensional computing: network templates for combined learning and classification of ExG signals
[J]. Proceedings of the IEEE , 2018 , 107 (1 ): 123 - 143 .
[本文引用: 1]
[35]
RAHIMI A, BENATTI S, KANERVA P, et al. Hyperdimensional biosignal processing: a case study for EMG-based hand gesture recognition[C]//Proc. of the IEEE International Conference on Rebooting Computing, 2016.
[本文引用: 3]
[36]
BURRELLO A , SCHINDLER K , BENINI L , et al . Hyperdimensional computing with local binary patterns: one-shot learning of seizure onset and identification of ictogenic brain regions using short-time iEEG recordings
[J]. IEEE Trans.on Biome-dical Engineering , 2019 , 67 (2 ): 601 - 613 .
[本文引用: 2]
[37]
KIM Y, IMANI M, MOSHIRI N, et al. GenieHD: efficient DNA pattern matching accelerator using hyperdimensional computing[C]//Proc. of the Design, Automation and Test in Europe Conference and Exhibition, 2020: 115-120.
[本文引用: 1]
[38]
CHANG C Y , CHUANG Y , CHANG E J , et al . MulTa-HDC: a multi-task learning framework for hyperdimensional computing
[J]. IEEE Trans.on Computers , 2021 , 70 (8 ): 1269 - 1284 .
DOI:10.1109/TC.2021.3073409
[本文引用: 1]
[39]
RÄSÄNEN O J , SAARINEN J P . Sequence prediction with sparse distributed hyperdimensional coding applied to the analysis of mobile phone use patterns
[J]. IEEE Trans.on Neural Networks and Learning Systems , 2015 , 27 (9 ): 1878 - 1889 .
[本文引用: 1]
[40]
RASANEN O , KAKOUROS S . Modeling dependencies in multiple parallel data streams with hyperdimensional computing
[J]. IEEE Signal Processing Letters , 2014 , 21 (7 ): 899 - 903 .
DOI:10.1109/LSP.2014.2320573
[41]
SCHLEGEL K, MIRUS F, NEUBERT P, et al. Multivariate time series analysis for driving style classification using neural networks and hyperdimensional computing[C]//Proc. of the IEEE Intelligent Vehicles Symposium, 2021: 602-609.
[本文引用: 1]
[42]
RAHIMI A, KANERVA P, MILLAN J R, et al. Hyperdimensional computing for noninvasive brain-computer interfaces: blind and one-shot classification of EEG error-related potentials[C]//Proc. of the ACM/EAI International Conference on Bio-inspired Information and Communications Technologies, 2017: 19-26.
[本文引用: 1]
[43]
IMANI M, MORRIS J, BOSCH S, et al. AdaptHD: adaptive efficient training for brain-inspired hyperdimensional computing[C]//Proc. of the IEEE Biomedical Circuits and Systems Conference, 2019.
[本文引用: 3]
[44]
RAHIMI A , DATTA S , KLEYKO D , et al . High-dimensional computing as a nanoscalable paradigm
[J]. IEEE Trans.on Circuits and Systems I: Regular Papers , 2017 , 64 (9 ): 2508 - 2521 .
DOI:10.1109/TCSI.2017.2705051
[本文引用: 1]
[45]
IMANI M, MESSERLY J, WU F, et al. A binary learning framework for hyperdimensional computing[C]//Proc. of the Design, Automation and Test in Europe Conference & Exhibition, 2019: 126-131.
[本文引用: 1]
[46]
SCHMUCK M , BENINI L , RAHIMI A . Hardware optimizations of dense binary hyperdimensional computing: remateria-lization of hypervectors, binarized bundling, and combinational associative memory
[J]. ACM Journal on Emerging Technologies in Computing Systems , 2019 , 15 (4 ): 32 .
[本文引用: 1]
[47]
SALAMAT S , IMANI M , ROSING T . Accelerating hyperdimensional computing on FPGAs by exploiting computational reuse
[J]. IEEE Trans.on Computers , 2020 , 69 (8 ): 1159 - 1171 .
DOI:10.1109/TC.2020.2992662
[本文引用: 1]
[48]
LI H, WU T F, RAHIMI A, et al. Hyperdimensional computing with 3D VRRAM in-memory kernels: device-architecture co-design for energy-efficient, error-resilient language recognition[C]//Proc. of the IEEE International Electron Devices Meeting, 2016.
[本文引用: 1]
[49]
WU T F, LI H, HUANG P C, et al. Brain-inspired computing exploiting carbon nanotube FETs and resistive RAM: hyperdimensional computing case study[C]//Proc. of the IEEE International Solid-State Circuits Conference, 2018: 492-494.
[本文引用: 1]
[50]
KARUNARATNE G , LE-GALLO M , CHERUBINI G , et al . In-memory hyperdimensional computing
[J]. Nature Electro-nics , 2020 , 3 (6 ): 327 - 337 .
DOI:10.1038/s41928-020-0410-3
[本文引用: 1]
[51]
HOPFIELD J J . Neural networks and physical systems with emergent collective computational abilities
[J]. Proceedings of the National Academy of Sciences , 1982 , 79 (8 ): 2554 - 2558 .
DOI:10.1073/pnas.79.8.2554
[本文引用: 1]
[52]
ACKLEY D H , HINTON G E , SEJNOWSKI T J . A learning algorithm for Boltzmann machines
[J]. Cognitive Science , 1985 , 9 (1 ): 147 - 169 .
DOI:10.1207/s15516709cog0901_7
[本文引用: 1]
[54]
HINTON G E , ANDERSON J A . Parallel models of associative memory: updated edition [M]. New York : Psychology Press , 2014 .
[本文引用: 1]
[55]
MINSKY M , PAPERT S . Perceptrons [M]. Cambridge : MIT Press , 1969 .
[本文引用: 1]
[56]
WERBOS P J . Backpropagation through time: what it does and how to do it
[J]. Proceedings of the IEEE , 1990 , 78 (10 ): 1550 - 1560 .
DOI:10.1109/5.58337
[本文引用: 1]
[57]
RUMELHART D E , HINTON G E , WILLIAMS R J . Learning representations by back-propagating errors
[J]. Nature , 1986 , 323 (6088 ): 533 - 536 .
DOI:10.1038/323533a0
[本文引用: 1]
[58]
LECUN Y , BOSER B , DENKER J S , et al . Backpropagation applied to handwritten zip code recognition
[J]. Neural Computation , 1989 , 1 (4 ): 541 - 551 .
DOI:10.1162/neco.1989.1.4.541
[本文引用: 1]
[59]
HINTON G E . Mapping part-whole hierarchies into connectionist networks
[J]. Artificial Intelligence , 1990 , 46 (1/2 ): 47 - 75 .
[本文引用: 1]
[60]
SMOLENSKY P . Tensor product variable binding and the representation of symbolic structures in connectionist systems
[J]. Artificial Intelligence , 1990 , 46 (1/2 ): 159 - 216 .
[本文引用: 1]
[61]
PLATE T A . Holographic reduced representations
[J]. IEEE Trans.on Neural Networks , 1995 , 6 (3 ): 623 - 641 .
DOI:10.1109/72.377968
[本文引用: 1]
[62]
KANERVA P. Binary spatter-coding of ordered k -tuples[C]//Proc. of the International Conference on Artificial Neural Networks, 1996: 869-873.
[本文引用: 1]
[63]
GAYLER R W. Multiplicative binding representation operators and analogy[C]//Proc. of the Workshop on Advances in Analogy Research: Integration of Theory and Data from the Cognitive Computational and Neural Sciences, 1998.
[本文引用: 1]
[64]
PLATE T A . Holographic reduced representations: distributed representation for cognitive structures [M]. Stanford : CSLI , 2003 .
[本文引用: 1]
[65]
LEVY S D, GAYLER R. Vector symbolic architectures: a new building material for artificial general intelligence[C]//Proc. of the Conference on Artificial General Intelligence, 2008: 414-418.
[本文引用: 1]
[66]
IMANI M, HUANG C, KONG D, et al. Hierarchical hyperdimensional computing for energy efficient classification[C]//Proc. of the ACM/ESDA/IEEE Design Automation Confe-rence, 2018.
[本文引用: 1]
[67]
QUASTHOFF U, RICHTER M, BIEMANN C. Corpus portal for search in monolingual corpora[C]//Proc. of the International Conference on Language Resources and Evaluation, 2006: 1799-1802.
[本文引用: 1]
[68]
KOEHN P. Europarl: a parallel corpus for statistical machine translation[C]//Proc. of the Machine Translation Summit X, 2005: 79-86.
[本文引用: 1]
[69]
KLEYKO D , OSIPOV E , SENIOR A , et al . Holographic graph neuron: a bioinspired architecture for pattern processing
[J]. IEEE Trans.on Neural Networks and Learning Systems , 2016 , 28 (6 ): 1250 - 1262 .
[本文引用: 3]
[70]
MANABAT A X, MARCELO C R, QUINQUITO A L, et al. Performance analysis of hyperdimensional computing for cha-racter recognition[C]//Proc. of the International Symposium on Multimedia and Communication Technology, 2019.
[本文引用: 1]
[71]
IMANI M, KIM Y, WORLEY T, et al. HDCluster: an accurate clustering using brain-inspired high-dimensional computing[C]//Proc. of the Design, Automation and Test in Europe Conference & Exhibition, 2019: 1591-1594.
[本文引用: 1]
[72]
KLEYKO D , RAHIMI A , RACHKOVSKIJ D A , et al . Classification and recall with binary hyperdimensional computing: tradeoffs in choice of density and mapping characteristics
[J]. IEEE Trans.on Neural Networks and Learning Systems , 2018 , 29 (12 ): 5880 - 5898 .
DOI:10.1109/TNNLS.2018.2814400
[本文引用: 1]
[73]
IMANI M, SALAMAT S, KHALEGHI B, et al. SparseHD: algorithm-hardware co-optimization for efficient high-dimensional computing[C]//Proc. of the IEEE 27th Annual International Symposium on Field-Programmable Custom Computing Machines, 2019: 190-198.
[本文引用: 1]
[74]
MITROKHIN A , SUTOR P , SUMMERS-STAY D , et al . Symbolic representation and learning with hyperdimensional computing
[J]. Frontiers in Robotics and AI , 2020 , 7 , 63 .
DOI:10.3389/frobt.2020.00063
[本文引用: 1]
[75]
ALONSO P, SHRIDHAR K, KLEYKO D, et al. HyperEmbed: tradeoffs between resources and performance in NLP tasks with hyperdimensional computing enabled embedding of n-gram statistics[C]//Proc. of the International Joint Conference on Neural Networks, 2021.
[本文引用: 1]
[76]
KLEYKO D , KHEFFACHE M , FRADY E P , et al . Density encoding enables resource-efficient randomly connected neural networks
[J]. IEEE Trans.on Neural Networks and Learning Systems , 2020 , 32 (8 ): 3777 - 3783 .
[77]
MORRIS J, LUI H W, STEWART K, et al. HyperSpike: hyperdimensional computing for more efficient and robust spiking neural networks[C]//Proc. of the 2022 Design, Automation & Test in Europe Conference & Exhibition, 2022: 664-669.
[78]
KLEYKO D , FRADY E P , KHEFFACHE M , et al . Integer echo state networks: efficient reservoir computing for digital hardware
[J]. IEEE Trans.on Neural Networks and Learning Systems , 2022 , 33 (4 ): 1688 - 1701 .
DOI:10.1109/TNNLS.2020.3043309
[本文引用: 1]
[79]
HSU P K, YU S. In-memory 3D NAND flash hyperdimensional computing engine for energy-efficient SARS-CoV-2 genome sequencing[C]//Proc. of the IEEE International Memory Workshop, 2022.
[本文引用: 1]
[80]
DUBREUIL T, AMARI P, BARRAUD S, et al. A novel 3D 1T1R RRAM architecture for memory-centric hyperdimensional computing[C]//Proc. of the IEEE International Memory Workshop, 2022.
[本文引用: 1]
[81]
DATTA S , ANTONIO R A G , ISON A R S , et al . A programmable hyper-dimensional processor architecture for human-centric IoT
[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems , 2019 , 9 (3 ): 439 - 452 .
DOI:10.1109/JETCAS.2019.2935464
[本文引用: 1]
The perceptron: a probabilistic model for information storage and organization in the brain
2
1958
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
... 人工智能这一名称诞生在1956年的达特茅斯会议上, 经过曲折且漫长的发展, 人工智能算法如今取得了令人瞩目的成果.早期的高维认知模型以线性模型为主.1957年, Rosenblatt[1 ] 用简单的加减法运算发明了感知机, 通过二元线性分类器实现最简单形式的前馈式人工神经网络.1972年Anderson[3 ] 和Kohonen[4 ] 提出了线性相关矩阵存储器理论, 其基本思想类似感知机中神经元之间的信息传递方式和联结结构, 假设神经元突触的相互作用是线性叠加的, 试图通过一个存储矩阵, 即权重矩阵, 构造一组神经元与另一组神经元之间的线性映射关系, 将需要分析处理的各种信息等同为权重矩阵的特征向量.然而对于复杂的认知行为来说, 线性模型的效果有限, 因此后续研究开始向非线性模型发展. ...
1
1986
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
A simple neural network generating an inte-ractive memory
2
1972
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
... 人工智能这一名称诞生在1956年的达特茅斯会议上, 经过曲折且漫长的发展, 人工智能算法如今取得了令人瞩目的成果.早期的高维认知模型以线性模型为主.1957年, Rosenblatt[1 ] 用简单的加减法运算发明了感知机, 通过二元线性分类器实现最简单形式的前馈式人工神经网络.1972年Anderson[3 ] 和Kohonen[4 ] 提出了线性相关矩阵存储器理论, 其基本思想类似感知机中神经元之间的信息传递方式和联结结构, 假设神经元突触的相互作用是线性叠加的, 试图通过一个存储矩阵, 即权重矩阵, 构造一组神经元与另一组神经元之间的线性映射关系, 将需要分析处理的各种信息等同为权重矩阵的特征向量.然而对于复杂的认知行为来说, 线性模型的效果有限, 因此后续研究开始向非线性模型发展. ...
Correlation matrix memories
2
1972
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
... 人工智能这一名称诞生在1956年的达特茅斯会议上, 经过曲折且漫长的发展, 人工智能算法如今取得了令人瞩目的成果.早期的高维认知模型以线性模型为主.1957年, Rosenblatt[1 ] 用简单的加减法运算发明了感知机, 通过二元线性分类器实现最简单形式的前馈式人工神经网络.1972年Anderson[3 ] 和Kohonen[4 ] 提出了线性相关矩阵存储器理论, 其基本思想类似感知机中神经元之间的信息传递方式和联结结构, 假设神经元突触的相互作用是线性叠加的, 试图通过一个存储矩阵, 即权重矩阵, 构造一组神经元与另一组神经元之间的线性映射关系, 将需要分析处理的各种信息等同为权重矩阵的特征向量.然而对于复杂的认知行为来说, 线性模型的效果有限, 因此后续研究开始向非线性模型发展. ...
Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position
2
1980
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
... 同时期中, 神经网络等连接主义模型也在感知机之后逐渐发展.1969年, Minsky等人[55 ] 在对感知机的分析中, 提出两大限制连接主义模型发展的缺陷: ①基本感知机无法处理异或回路; ②当时有限的计算机计算能力不足以完成大型多层神经网络的训练.1974年, Werbos首次提出了使用误差反向传播[56 ] 训练神经网络的方法, 有效解决了感知机无法处理异或回路的问题.1986年, Rumelhart等人[57 ] 将反向传播算法推广至多层神经网络, 但是由于计算机性能限制, 仍然难以实现网络的训练和计算.卷积、池化等目前连接主义人工智能算法中的常用概念在当时也被Fukushima[5 ] 引入, 以实现更好的特征提取和减少运算量的效果, 陆续诞生了如LeCun等人在1989年提出的使用反向传播进行训练的卷积神经网络[58 ] 等经典模型. ...
Emergence of simple-cell receptive field properties by learning a sparse code for natural images
1
1996
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
An information-maximization approach to blind separation and blind deconvolution
1
1995
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
1
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
1
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
1
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
Deep neural networks for acoustic modeling in speech recognition: the shared views of four research groups
1
2012
... 如何使计算机具有和人脑类似甚至更好的记忆、学习、联想、认知和思考能力, 是长期以来广大研究人员共同希望解决的难题之一.神经科学在寻求解释人类神智活动的同时, 也为机器学习领域提供了丰富的灵感来源, 并由此衍生出了一系列类人脑人工智能算法.例如, 从神经细胞间信息传递模型抽象出的单层感知机[1 ] 和在其基础上发展的深度神经网络[2 ] , 假定神经元突触相互作用是线性累加的相关矩阵存储器(correlation matrix memories, CMM)[3 -4 ] , 受视网膜神经元感受野启发的卷积神经网络[5 ] , 借鉴大脑激活稀疏性的稀疏编码[6 ] , 以及模拟大脑如何在嘈杂环境中将注意力集中到某个特定声音的独立成分分析(independent component analysis, ICA)算法[7 ] 等.其中, 神经网络在被提出初期, 由于其较大的模型规模和当时有限的计算机算力, 模型训练困难, 准确率有限.直到2012年基于深度卷积神经网络的AlexNet模型[8 ] 取得突破性进展后, 神经网络的相关研究在图像识别[9 ] 、自然语言处理[10 ] 、语音识别[11 ] 等诸多领域得到了广泛应用, 以神经网络为代表的连接主义模型迅速成为了人工智能领域的研究热点. ...
One-shot learning of object categories
1
2006
... 随着需要处理的任务难度不断上升, 神经网络模型不断向着更深、更广、更复杂的趋势发展.但是, 这一趋势直接使神经网络的模型规模越来越庞大.目前, 常用的神经网络模型, 需要训练的参数量一般都在百万以上.巨大运算量带来的漫长训练时间对硬件设备的精度和性能要求较高, 也需要更多的能耗和更好的模型稳定性.较低的硬件友好性也使神经网络很难在物联网、嵌入式系统等小型平台上完成实时片上训练.此外, 神经网络模型的训练依赖大数据驱动、无指标调参和浮点数迭代运算, 而大脑产生认知并执行决策时所需样本很少, 快速联想能力强且容错性高, 两者存在着本质差异.虽然在很多实际应用中, 黑匣式神经网络模型做出的决策判断取得了良好的识别效果, 但目前神经网络模型提取的特征和产生决策的具体逻辑仍然在语义层面难以理解, 并且缺乏标准的数学工具定量评估模型的泛化能力和实际学习能力, 其可信度和可解释性有限.大量工作围绕解决神经网络算法存在的上述问题开展, 例如减少样本需求并加速训练过程的小样本学习[12 ] 、简化模型结构的剪枝技术[13 ] 、增加模型可解释性的可视化技术[14 -15 ] 等. ...
1
... 随着需要处理的任务难度不断上升, 神经网络模型不断向着更深、更广、更复杂的趋势发展.但是, 这一趋势直接使神经网络的模型规模越来越庞大.目前, 常用的神经网络模型, 需要训练的参数量一般都在百万以上.巨大运算量带来的漫长训练时间对硬件设备的精度和性能要求较高, 也需要更多的能耗和更好的模型稳定性.较低的硬件友好性也使神经网络很难在物联网、嵌入式系统等小型平台上完成实时片上训练.此外, 神经网络模型的训练依赖大数据驱动、无指标调参和浮点数迭代运算, 而大脑产生认知并执行决策时所需样本很少, 快速联想能力强且容错性高, 两者存在着本质差异.虽然在很多实际应用中, 黑匣式神经网络模型做出的决策判断取得了良好的识别效果, 但目前神经网络模型提取的特征和产生决策的具体逻辑仍然在语义层面难以理解, 并且缺乏标准的数学工具定量评估模型的泛化能力和实际学习能力, 其可信度和可解释性有限.大量工作围绕解决神经网络算法存在的上述问题开展, 例如减少样本需求并加速训练过程的小样本学习[12 ] 、简化模型结构的剪枝技术[13 ] 、增加模型可解释性的可视化技术[14 -15 ] 等. ...
1
... 随着需要处理的任务难度不断上升, 神经网络模型不断向着更深、更广、更复杂的趋势发展.但是, 这一趋势直接使神经网络的模型规模越来越庞大.目前, 常用的神经网络模型, 需要训练的参数量一般都在百万以上.巨大运算量带来的漫长训练时间对硬件设备的精度和性能要求较高, 也需要更多的能耗和更好的模型稳定性.较低的硬件友好性也使神经网络很难在物联网、嵌入式系统等小型平台上完成实时片上训练.此外, 神经网络模型的训练依赖大数据驱动、无指标调参和浮点数迭代运算, 而大脑产生认知并执行决策时所需样本很少, 快速联想能力强且容错性高, 两者存在着本质差异.虽然在很多实际应用中, 黑匣式神经网络模型做出的决策判断取得了良好的识别效果, 但目前神经网络模型提取的特征和产生决策的具体逻辑仍然在语义层面难以理解, 并且缺乏标准的数学工具定量评估模型的泛化能力和实际学习能力, 其可信度和可解释性有限.大量工作围绕解决神经网络算法存在的上述问题开展, 例如减少样本需求并加速训练过程的小样本学习[12 ] 、简化模型结构的剪枝技术[13 ] 、增加模型可解释性的可视化技术[14 -15 ] 等. ...
A survey on neural network interpretability
1
2021
... 随着需要处理的任务难度不断上升, 神经网络模型不断向着更深、更广、更复杂的趋势发展.但是, 这一趋势直接使神经网络的模型规模越来越庞大.目前, 常用的神经网络模型, 需要训练的参数量一般都在百万以上.巨大运算量带来的漫长训练时间对硬件设备的精度和性能要求较高, 也需要更多的能耗和更好的模型稳定性.较低的硬件友好性也使神经网络很难在物联网、嵌入式系统等小型平台上完成实时片上训练.此外, 神经网络模型的训练依赖大数据驱动、无指标调参和浮点数迭代运算, 而大脑产生认知并执行决策时所需样本很少, 快速联想能力强且容错性高, 两者存在着本质差异.虽然在很多实际应用中, 黑匣式神经网络模型做出的决策判断取得了良好的识别效果, 但目前神经网络模型提取的特征和产生决策的具体逻辑仍然在语义层面难以理解, 并且缺乏标准的数学工具定量评估模型的泛化能力和实际学习能力, 其可信度和可解释性有限.大量工作围绕解决神经网络算法存在的上述问题开展, 例如减少样本需求并加速训练过程的小样本学习[12 ] 、简化模型结构的剪枝技术[13 ] 、增加模型可解释性的可视化技术[14 -15 ] 等. ...
Theoretical foundations of hyperdimensional computing
3
2021
... 然而, 这些在神经网络模型中需要通过额外处理才能在特定情况下实现的特性, 直接且自然地存在于超维计算基本架构中[16 ] .因此, 虽然超维计算的理论雏形早在20世纪80年代就被提出[17 ] , 在近年来也作为一种新兴技术重新得到了全球范围内的关注和系统性的研究. ...
... 在超维计算中, 每一个实体都被编码映射为一个超维向量, 即一个维度为数千、数万或更高的高维矢量.实体的信息被全息地分布在超维向量中的每个元素上, 每个元素之间几乎是独立的.在超维向量所在的超维空间中, 通过对向量进行加法、乘法和排列等简单运算即可产生丰富且具有特殊性质的数学计算行为[16 ] , 进而实现后续的高能效、高鲁棒性认知操作[22 -25 ] .在实际应用中, 超维向量的运算通常由简单高效的逐位二进制整数运算实现.模型不依赖于大数据驱动, 对每个样本通过一次编码映射即可完成训练, 使超维计算所需的运算成本和对硬件性能的要求极低, 具有超快速的训练时间和数据刷新率.其硬件友好性使小成本片上训练成为可能, 并且在获得新样本时, 已有模型可以实时更新与学习.同时, 由于超维计算中的运算都是可逆的, 模型也具有良好的可验证性和可解释性. ...
... 2008年, Levy[65 ] 将以高维、分布式数据表示作为识别基础的计算模型统称为矢量符号架构(vector symbolic architectures, VSA), 涵盖了全息简化表示、飞溅码等诸多理论.矢量符号架构作为一种新型人工智能架构, 提供了一种系统的方式来生成和操作各类信息的高维表示来完成认知操作.超维计算是矢量符号架构等早期模型的继承者, 在硬件效率方面有着很强的附加优势[16 ] .超维计算中的大量概念和思想也同样适用于矢量符号架构模型, 因此矢量符号架构也常被作为超维计算的别称之一. ...
3
1988
... 然而, 这些在神经网络模型中需要通过额外处理才能在特定情况下实现的特性, 直接且自然地存在于超维计算基本架构中[16 ] .因此, 虽然超维计算的理论雏形早在20世纪80年代就被提出[17 ] , 在近年来也作为一种新兴技术重新得到了全球范围内的关注和系统性的研究. ...
... 通过压缩函数可以将线性相关矩阵存储器算法中使用的输出向量转化为点吸引子的形式, 实现模型的非线性化.著名的Hopfield网络[51 ] 采用的就是这种方式, 其核心功能是将残缺输入数据通过联想关联重建为完整数据, 具有较好的识别性能和鲁棒性.后续发展为玻尔兹曼机[52 ] 和深度置信网络[53 ] (deep belief network, DBN), 对人工智能领域产生了深远影响.然而, Hopfield网络的存储容量是有限的.例如, 具有N 个神经元的二进制Hopfield网络, 其最大可存储模式为2N [54 ] 围绕联想存储器展开的工作基础上, Kanerva[17 ] 在1988年提出了稀疏分布式存储理论, 通过引入随机权值的方式, 使用固定尺寸的权重矩阵就可以构造无限容量的联想存储器系统, 这也被认为是超维计算存储结构的直接理论雏形之一. ...
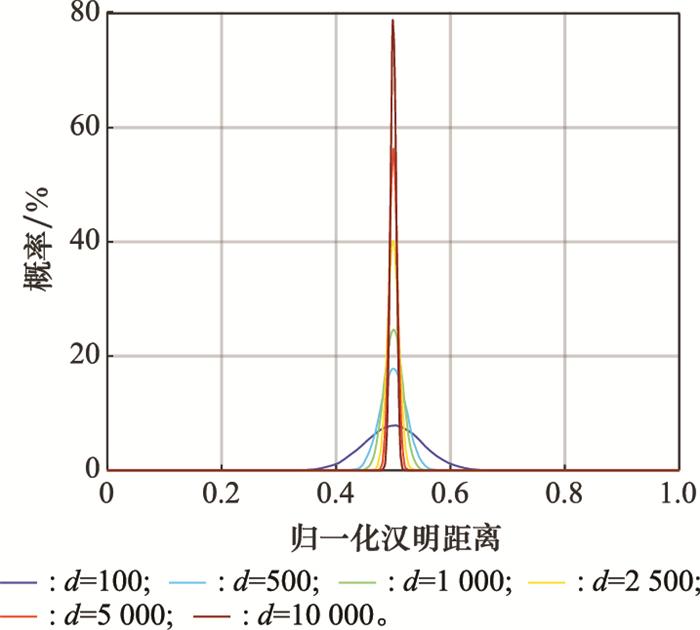
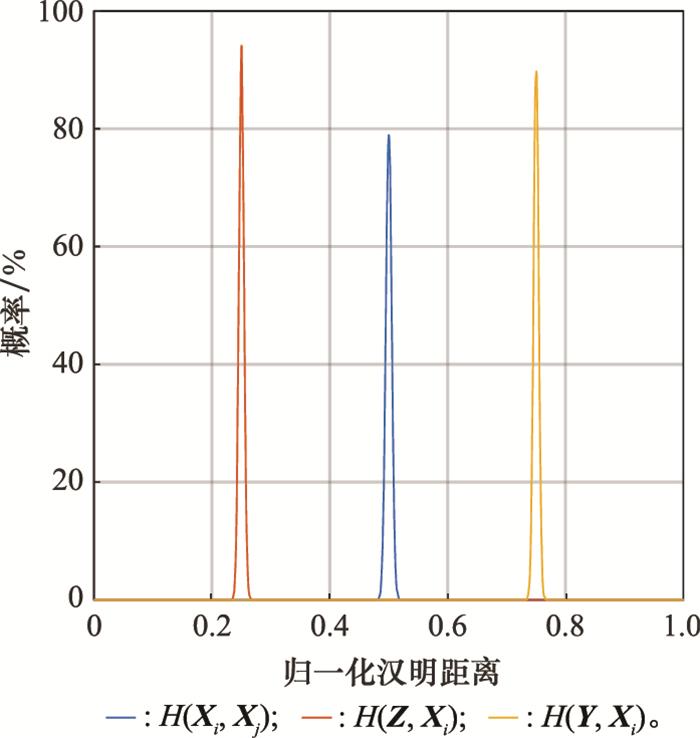
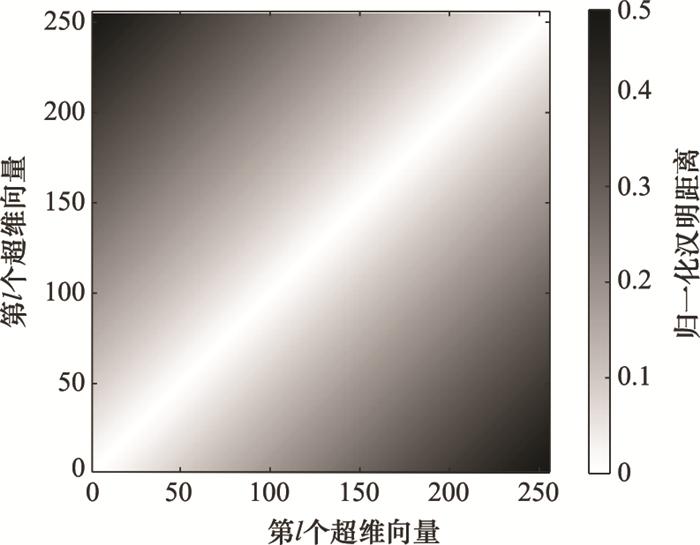
... 如图 3 所示, 如果在超维空间中任意选取一对采用二元数据类型进行编码的超维向量, 其归一化汉明距离的概率密度函数将集中在0.5左右, 且集中程度随着维数的增大而增大.根据统计, 当d =10 000时, 使用二进制编码或双极编码的一个超维向量与其他(210 000 -1)个超维向量之间的归一化汉明距离中, 仅有百万分之一小于0.476或大于0.524, 仅有十亿分之一小于0.470或大于0.530[17 ] .这一特点表明, 在概率上, 几乎所有互相之间不存在关联的超维向量对之间的归一化汉明距离都为0.5左右, 而更靠近0和更靠近1的归一化汉明距离只有通过人为设置或运算操作才可能出现. ...
Hyperdimensional computing: an introduction to computing in distributed representation with high-dimensional random vectors
5
2009
... 超维计算[18 ] 同样是理论神经科学与计算机科学交叉领域的产物.与上文提到的神经网络等人工智能算法相比, 相同之处在于其都将信息的高维分布式表示作为数据的表示方式或处理过程中的基本环节.生物学中的相关研究表明, 许多生物的感觉系统中都有一个将相对低维的感觉输入信号转化为高维稀疏表示的器官, 并使用此高维表示实现后续的认知行为[19 -20 ] , 此特点与这些算法中高维的概念相符.不同之处在于, 超维计算将记忆的产生和回忆看作是一种高维的全局随机映射与相似度匹配, 类似大脑中海马体将短时记忆信息经过加工转化后形成大脑皮层长时记忆的方式[21 ] , 将新信息通过联想、筛选和整合, 添加至已有的信息编码中, 这与神经网络等连接主义模型中的多层复合数值运算不同. ...
... 2009年, Kanerva[18 ] 将矢量符号架构中的早期模型进行整合, 以教程文章的形式首次正式提出超维计算的系统性理论与基本原理.Kanerva[18 ] 介绍了超维计算的模型结构和模型背后的主要思想, 对超维计算的性质、数据编码规则、具体运算方法和不同场景下的使用方式进行了详细说明, 并给出了实际应用示例.在极低的运算成本和计算资源需求下, 超维计算通过简单的算术运算和一次映射就可以在超维空间中实现对事物的高效识别、学习和认知, 这一性质使超维计算在计算资源有限的应用场景中作为轻量级分类器展现出极大潜力. ...
... [18 ]介绍了超维计算的模型结构和模型背后的主要思想, 对超维计算的性质、数据编码规则、具体运算方法和不同场景下的使用方式进行了详细说明, 并给出了实际应用示例.在极低的运算成本和计算资源需求下, 超维计算通过简单的算术运算和一次映射就可以在超维空间中实现对事物的高效识别、学习和认知, 这一性质使超维计算在计算资源有限的应用场景中作为轻量级分类器展现出极大潜力. ...
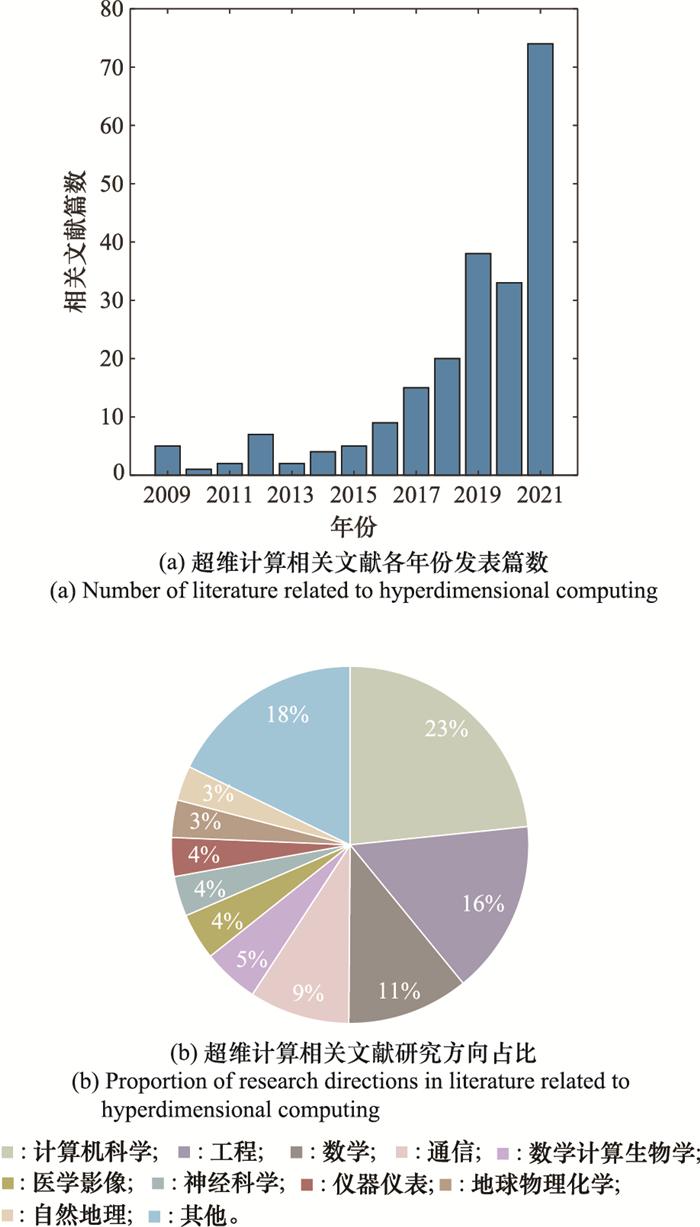
... 可以看出, 自2009年Kanerva在文献[18 ]中正式提出超维计算的概念和原理以来, 超维计算相关文献每年的发表篇数保持着快速上升趋势, 并在近年来得到全球范围内研究人员越来越多的关注, 未来一段时间内仍有着巨大的发展空间和研究价值.除计算机科学外, 超维计算得到应用的研究方向还包括了工程、数学、通信、数学计算生物学、神经科学、医学影像、仪器仪表、地球物理化学等领域, 适用情景非常丰富. ...
... 在几何意义上, 乘法运算相当于将超维空间中的两个点绑定后作为一个整体映射到空间中的另一个位置, 过程中保持点与点之间的汉明距离[18 ] .这很类似于数学中自变量与因变量的绑定, 或者是计算机中地址与数值的绑定.因此, 乘法运算常被用来绑定一个地址-数值对.例如, 将式(6)中的A B A
Olfactory information processing in Drosophila
1
2009
... 超维计算[18 ] 同样是理论神经科学与计算机科学交叉领域的产物.与上文提到的神经网络等人工智能算法相比, 相同之处在于其都将信息的高维分布式表示作为数据的表示方式或处理过程中的基本环节.生物学中的相关研究表明, 许多生物的感觉系统中都有一个将相对低维的感觉输入信号转化为高维稀疏表示的器官, 并使用此高维表示实现后续的认知行为[19 -20 ] , 此特点与这些算法中高维的概念相符.不同之处在于, 超维计算将记忆的产生和回忆看作是一种高维的全局随机映射与相似度匹配, 类似大脑中海马体将短时记忆信息经过加工转化后形成大脑皮层长时记忆的方式[21 ] , 将新信息通过联想、筛选和整合, 添加至已有的信息编码中, 这与神经网络等连接主义模型中的多层复合数值运算不同. ...
Random convergence of olfactory inputs in the Drosophila mushroom body
1
2013
... 超维计算[18 ] 同样是理论神经科学与计算机科学交叉领域的产物.与上文提到的神经网络等人工智能算法相比, 相同之处在于其都将信息的高维分布式表示作为数据的表示方式或处理过程中的基本环节.生物学中的相关研究表明, 许多生物的感觉系统中都有一个将相对低维的感觉输入信号转化为高维稀疏表示的器官, 并使用此高维表示实现后续的认知行为[19 -20 ] , 此特点与这些算法中高维的概念相符.不同之处在于, 超维计算将记忆的产生和回忆看作是一种高维的全局随机映射与相似度匹配, 类似大脑中海马体将短时记忆信息经过加工转化后形成大脑皮层长时记忆的方式[21 ] , 将新信息通过联想、筛选和整合, 添加至已有的信息编码中, 这与神经网络等连接主义模型中的多层复合数值运算不同. ...
Memory and the hippocampus: a synthesis from findings with rats, monkeys, and humans
1
1992
... 超维计算[18 ] 同样是理论神经科学与计算机科学交叉领域的产物.与上文提到的神经网络等人工智能算法相比, 相同之处在于其都将信息的高维分布式表示作为数据的表示方式或处理过程中的基本环节.生物学中的相关研究表明, 许多生物的感觉系统中都有一个将相对低维的感觉输入信号转化为高维稀疏表示的器官, 并使用此高维表示实现后续的认知行为[19 -20 ] , 此特点与这些算法中高维的概念相符.不同之处在于, 超维计算将记忆的产生和回忆看作是一种高维的全局随机映射与相似度匹配, 类似大脑中海马体将短时记忆信息经过加工转化后形成大脑皮层长时记忆的方式[21 ] , 将新信息通过联想、筛选和整合, 添加至已有的信息编码中, 这与神经网络等连接主义模型中的多层复合数值运算不同. ...
3
... 在超维计算中, 每一个实体都被编码映射为一个超维向量, 即一个维度为数千、数万或更高的高维矢量.实体的信息被全息地分布在超维向量中的每个元素上, 每个元素之间几乎是独立的.在超维向量所在的超维空间中, 通过对向量进行加法、乘法和排列等简单运算即可产生丰富且具有特殊性质的数学计算行为[16 ] , 进而实现后续的高能效、高鲁棒性认知操作[22 -25 ] .在实际应用中, 超维向量的运算通常由简单高效的逐位二进制整数运算实现.模型不依赖于大数据驱动, 对每个样本通过一次编码映射即可完成训练, 使超维计算所需的运算成本和对硬件性能的要求极低, 具有超快速的训练时间和数据刷新率.其硬件友好性使小成本片上训练成为可能, 并且在获得新样本时, 已有模型可以实时更新与学习.同时, 由于超维计算中的运算都是可逆的, 模型也具有良好的可验证性和可解释性. ...
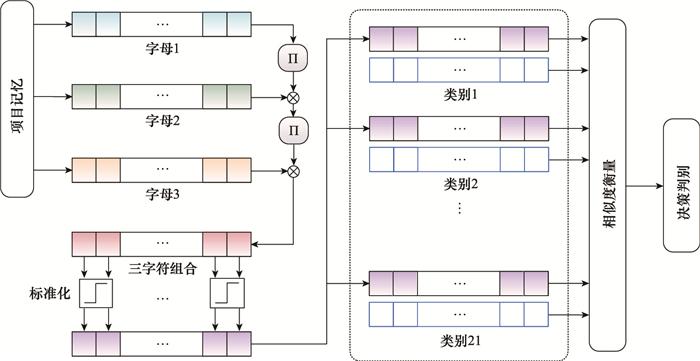
... 欧洲国家的语言一般都由字母组成, 识别出任意一段文字具体是由哪个国家的语言写成的是自然语言处理中的一个经典问题.基于三字符组合频率直方图的方法是传统识别途径之一, 对于26个字母和空格, 共27个字符来说, 每三个字符为一组共有273 种可能的组合方式.该方法扫描一段文字中每三个字符的组合, 将一段文字中各种组合情况的出现次数记录在273 维的个数向量对应位置中, 最终构成一个组合频率直方图, 通过测试样本和训练样本的组合频率直方图相似度对比完成识别.但这种方法随着选择不同数量的字符组合作为识别依据时, 直方图的维度将指数级上升, 占用更多的存储空间和计算资源.超维计算可以有效解决上述问题[22 , 30 -31 ] , 基本处理流程如图 14 所示. ...
... 文献[22 ]对欧洲21国语言进行了分类, 基于Wortschatz语料库[67 ] 中约一百万字节的文本训练得到每个国家语言的样本超维向量, 使用Europarl语料库[68 ] 中每个国家各1 000个单独句子作为测试样本, 最终的平均识别准确率为96.7%, 以传统机器学习一半的运算成本和能耗实现了仅比传统机器学习方法低1.2%的准确率, 且具有比传统机器学习方法更好的容错率.文献[31 ]将该算法移植至新兴纳米技术集成电路芯片, 实现了20 000个单独句子98%的准确率. ...
Near-channel classifier: symbiotic communication and classification in high-dimensional space
0
2021
Robust high-dimensional memory-augmented neural networks
1
2021
... 在超维计算中, 每一个实体都被编码映射为一个超维向量, 即一个维度为数千、数万或更高的高维矢量.实体的信息被全息地分布在超维向量中的每个元素上, 每个元素之间几乎是独立的.在超维向量所在的超维空间中, 通过对向量进行加法、乘法和排列等简单运算即可产生丰富且具有特殊性质的数学计算行为[16 ] , 进而实现后续的高能效、高鲁棒性认知操作[22 -25 ] .在实际应用中, 超维向量的运算通常由简单高效的逐位二进制整数运算实现.模型不依赖于大数据驱动, 对每个样本通过一次编码映射即可完成训练, 使超维计算所需的运算成本和对硬件性能的要求极低, 具有超快速的训练时间和数据刷新率.其硬件友好性使小成本片上训练成为可能, 并且在获得新样本时, 已有模型可以实时更新与学习.同时, 由于超维计算中的运算都是可逆的, 模型也具有良好的可验证性和可解释性. ...
Radar-based human activity recognition using hyperdimensional computing
6
2022
... 总的来说, 超维计算以其更快的学习过程、更低的延迟率、更高的能效、更贴合神经科学的鲁棒性、更轻量的模型规模、更少的样本需求和更多的可解释特征, 成为一种极具前途的片上实时学习和识别方法[26 ] , 从基本架构上直接解决了神经网络等人工智能算法存在的问题, 作为一种新兴轻量级分类器提供了辅助甚至取代现有传统机器学习方法的可能性[27 -28 ] .目前, 有关超维计算的系统理论、工程应用以及与其他算法配合使用的研究仍然处在快速发展阶段. ...
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
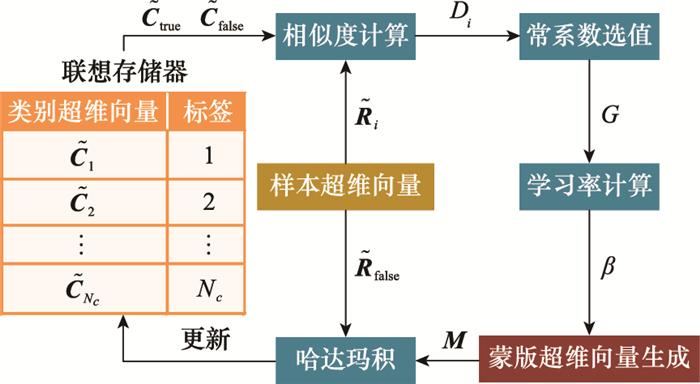
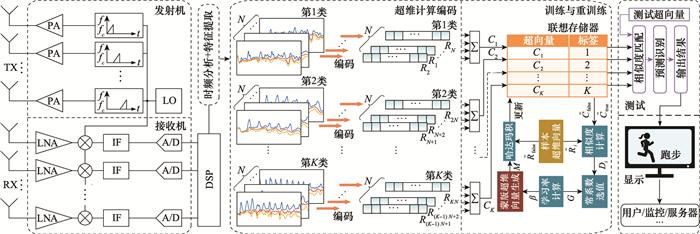
... 蒙版重训练[26 ] 方法进一步解决了上述问题, 其基本原理受AdaptHD启发, 整体流程如图 12 所示. ...
... 文献[26 ]中使用毫米波雷达对6种不同的实测人体姿态进行探测, 并基于超维计算模型完成高效快速识别.结合雷达频谱图像的实际特点, 文献[26 ]选择提取包络的方式保留频谱图中的微多普勒特征和空间能量关系, 在大幅减少待处理数据量的同时, 获得了一维结构的包络数据输入超维计算进行后续编码与识别.在完成一次初步训练后, 进一步通过式(22)的蒙版重训练方法调整和完善模型, 整体处理流程如图 17 所示.实验结果显示, 蒙版重训练仅额外花费约3.4%的总训练时间, 将平均识别准确率从不使用重训练方法时的83.2%有效提升至92.9%.在对比实验中, 超维计算的识别准确率超过了大部分传统分类器, 并且与识别准确率相近的神经网络模型相比, 超维计算模型的平均训练速度快4.1倍以上.在样本数较少和数据点有限等情况下, 超维计算仍然表现出较强的稳定性和鲁棒性, 准确率与训练时间上的优势将更加明显. ...
... ]中使用毫米波雷达对6种不同的实测人体姿态进行探测, 并基于超维计算模型完成高效快速识别.结合雷达频谱图像的实际特点, 文献[26 ]选择提取包络的方式保留频谱图中的微多普勒特征和空间能量关系, 在大幅减少待处理数据量的同时, 获得了一维结构的包络数据输入超维计算进行后续编码与识别.在完成一次初步训练后, 进一步通过式(22)的蒙版重训练方法调整和完善模型, 整体处理流程如图 17 所示.实验结果显示, 蒙版重训练仅额外花费约3.4%的总训练时间, 将平均识别准确率从不使用重训练方法时的83.2%有效提升至92.9%.在对比实验中, 超维计算的识别准确率超过了大部分传统分类器, 并且与识别准确率相近的神经网络模型相比, 超维计算模型的平均训练速度快4.1倍以上.在样本数较少和数据点有限等情况下, 超维计算仍然表现出较强的稳定性和鲁棒性, 准确率与训练时间上的优势将更加明显. ...
... (3) 更好的预处理方法.对于第5.1节中的第二个问题, 在输入超维计算前提前使用一些高效的预处理方法是有效的.预处理可以实现减少数据量, 去除冗余信息, 保留核心特征数据等功能, 这也对提高最终的识别准确率有一定的帮助.对于图像等数据而言, 可以使用类似包络提取[26 , 35 ] 、投影变换、稀疏表示[73 ] 、主成分分析等特征提取方法将原始数据转化为向量形式或降低待处理数据量后再进行编码.甚至可以如文献[74 ]中通过哈希神经网络产生图像的高维表示, 直接作为样本超维向量输入超维计算进行训练和测试, 也可以取得良好的识别效果.但值得注意和思考的是, 如何在通过额外计算量以完成预处理和保持超维计算的轻量化快速认知模型之间保持平衡. ...
Classification using hyperdimensional computing: a review
4
2020
... 总的来说, 超维计算以其更快的学习过程、更低的延迟率、更高的能效、更贴合神经科学的鲁棒性、更轻量的模型规模、更少的样本需求和更多的可解释特征, 成为一种极具前途的片上实时学习和识别方法[26 ] , 从基本架构上直接解决了神经网络等人工智能算法存在的问题, 作为一种新兴轻量级分类器提供了辅助甚至取代现有传统机器学习方法的可能性[27 -28 ] .目前, 有关超维计算的系统理论、工程应用以及与其他算法配合使用的研究仍然处在快速发展阶段. ...
... 当奇数个超维向量相加时不会出现歧义, 直接将和超维向量$\tilde{\boldsymbol{R}}$ N , 通过对比该均值与1/2的大小关系进行阈值处理即可.但当偶数个超维向量相加时, 在某些位上可能会出现加数超维向量中0的个数与1的个数完全相同的情况.此时, 该位计算得到的均值将正好等于1/2.实验表明, 在超维计算中当维数较高时, 这些位上数值是选择0还是选择1对整个加法运算几乎没有影响[27 ] , 因此这些位在标准化处理中常采用随机选择的方式.给出3个二进制编码的8维向量进行加法运算的例子如下: ...
... 式中: 除了第一项H 1 ⊕H 1 ⊕V 1 以外的项, 根据超维向量的正交性可以视为噪声, 在高维度中对V 1 的影响可以近似忽略[27 ] . ...
... (1) 最高识别准确率一般低于基于神经网络的连接主义模型.虽然在计算资源有限的平台中, 在相同的训练时间, 或在可用样本数量较少等情况下, 超维计算的准确率可以接近甚至高于神经网络及其他分类识别算法.但是, 在不考虑计算成本的情况下, 除了例如文献[36 ]研究的癫痫病发作检测和文献[71 ]研究的乳腺癌识别等部分应用领域外, 超维计算的识别准确率一般低于连接主义算法, 且由于超维计算的模型和参数较为简单, 在相对固定的模型框架下准确率也相对固定, 最高准确率难以进一步提升.因此, 文献[27 ]将超维计算的识别准确率称为是一种可接受的准确率. ...
Hyper-dimensional computing challenges and opportunities for AI applications
2
2021
... 总的来说, 超维计算以其更快的学习过程、更低的延迟率、更高的能效、更贴合神经科学的鲁棒性、更轻量的模型规模、更少的样本需求和更多的可解释特征, 成为一种极具前途的片上实时学习和识别方法[26 ] , 从基本架构上直接解决了神经网络等人工智能算法存在的问题, 作为一种新兴轻量级分类器提供了辅助甚至取代现有传统机器学习方法的可能性[27 -28 ] .目前, 有关超维计算的系统理论、工程应用以及与其他算法配合使用的研究仍然处在快速发展阶段. ...
... 从上述相关应用和研究中可以发现, 超维计算更擅长处理一维结构(序列、矢量)的数据, 而在处理二维结构(图像)的数据上优势暂时还不明显[28 ] .因此, 现有图像识别应用中超维计算处理的对象大部分仍然是尺寸较小的简单图像, 以验证可行性.对于更复杂图像的处理方式, 有待进一步研究. ...
3
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
... 重训练的概念由Imani等人在2017年提出[29 ] , 通过增量更新类别超维向量, 避免由于向单个类别超维向量添加大量样本超维向量而导致的信息容量问题和准确率下降问题, 修正模型由于编码、样本质量、错误标签等各种原因导致的对某些训练样本的错误认知. ...
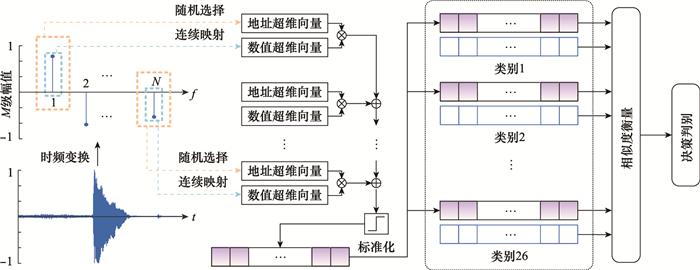
... 语音识别是人机交互、智能家居、机器翻译等领域中的重要环节之一, 超维计算在轻量级物联网平台的语音识别中展现出超高能效和学习速度.文献[29 ]首次将超维计算用于语音识别中, 提出了VoiceHD算法, 处理流程如图 13 所示. ...
2
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
... 欧洲国家的语言一般都由字母组成, 识别出任意一段文字具体是由哪个国家的语言写成的是自然语言处理中的一个经典问题.基于三字符组合频率直方图的方法是传统识别途径之一, 对于26个字母和空格, 共27个字符来说, 每三个字符为一组共有273 种可能的组合方式.该方法扫描一段文字中每三个字符的组合, 将一段文字中各种组合情况的出现次数记录在273 维的个数向量对应位置中, 最终构成一个组合频率直方图, 通过测试样本和训练样本的组合频率直方图相似度对比完成识别.但这种方法随着选择不同数量的字符组合作为识别依据时, 直方图的维度将指数级上升, 占用更多的存储空间和计算资源.超维计算可以有效解决上述问题[22 , 30 -31 ] , 基本处理流程如图 14 所示. ...
Low-power sparse hyperdimensional encoder for language recognition
3
2017
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
... 欧洲国家的语言一般都由字母组成, 识别出任意一段文字具体是由哪个国家的语言写成的是自然语言处理中的一个经典问题.基于三字符组合频率直方图的方法是传统识别途径之一, 对于26个字母和空格, 共27个字符来说, 每三个字符为一组共有273 种可能的组合方式.该方法扫描一段文字中每三个字符的组合, 将一段文字中各种组合情况的出现次数记录在273 维的个数向量对应位置中, 最终构成一个组合频率直方图, 通过测试样本和训练样本的组合频率直方图相似度对比完成识别.但这种方法随着选择不同数量的字符组合作为识别依据时, 直方图的维度将指数级上升, 占用更多的存储空间和计算资源.超维计算可以有效解决上述问题[22 , 30 -31 ] , 基本处理流程如图 14 所示. ...
... 文献[22 ]对欧洲21国语言进行了分类, 基于Wortschatz语料库[67 ] 中约一百万字节的文本训练得到每个国家语言的样本超维向量, 使用Europarl语料库[68 ] 中每个国家各1 000个单独句子作为测试样本, 最终的平均识别准确率为96.7%, 以传统机器学习一半的运算成本和能耗实现了仅比传统机器学习方法低1.2%的准确率, 且具有比传统机器学习方法更好的容错率.文献[31 ]将该算法移植至新兴纳米技术集成电路芯片, 实现了20 000个单独句子98%的准确率. ...
2
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
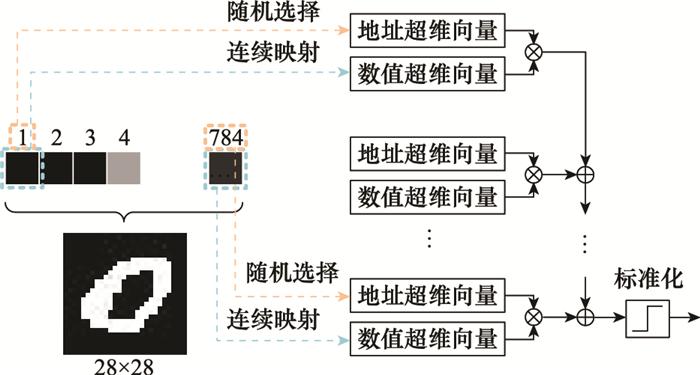
... 更一般地, 文献[32 ]将超维计算用于尺寸为28×28像素美国国家标准与技术研究院混合数据集(Mixed National Institute of Standards and Technolog Database, MNIST)手写数字图像数据集的识别中.文中采用双极编码方式, 将灰度像素所在的共784个位置编码为地址超维向量, [0, 255]的灰度值使用连续映射编码为数值超维向量, 处理流程相当于将图像按行或按列直接展开为向量的形式, 使用第3.1节中对语音信号记录型样本编码的方式编码手写数字图像, 整体处理流程如图 16 所示.该算法在极短的训练时间内识别准确率可以达到约90%, 并通过生成对抗性输入的方式重训练超维计算模型, 大幅增强了模型的鲁棒性和可靠性. ...
Fast SAR image recog-nition via hyperdimensional computing using monogenic mapping
3
2022
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
... 基于第2节的背景知识, 在超维空间中, 通过对超维向量的操作可以产生丰富的计算行为, 为编码、学习和认知更复杂的样本数据和信息提供基础.超维计算的模型不同于连接主义模型, 在简单、快速、高效的同时, 框架也相对固定, 编码过程是影响最终的模型效果的核心环节.正如文献[33 ]中所说, 超维计算的性能完全取决于模型架构的设计, 而不是模型的具体训练过程, 这也是超维计算不同于连接主义模型之处. ...
... 文献[33 ]首先通过单演信号分析方法, 将合成孔径雷达图像变换为基本不随目标配置、姿态角、俯仰角、随机噪声污染、遮挡等因素变化的多尺度高维解析信号, 转化为一维向量的形式, 然后使用主成分分析减少冗余数据后, 使用张量积进行高维映射编码并输入超维计算.该方法在运动和静止目标获取与识别(moving and stationary target acquisition and recognition, MSTAR)公开数据集中, 以极低的参数量和运算量实现了对合成孔径雷达图像10类目标的超快速、高准确率识别, 与现有算法相比, 在保证最终识别准确率的同时, 进一步将运算量降低了2~5个数量级. ...
Efficient biosignal processing using hyperdimensional computing: network templates for combined learning and classification of ExG signals
1
2018
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
3
... 地址中存储的数值则与独立地址不同, 数值可以代表个数、幅值、质量、灰度等信息, 在同一范围内的数值之间并不是完全独立的, 例如0~5 V的电压、50~100 g的质量等.每个范围内通常包含着多个相互关联的数值, 具体的离散点个数由采样精度决定.连续映射[35 ] 是将同一范围内的多个数值映射到超维空间中的一种有效方法. ...
... 现有的样本编码方法中, 主要将数据按两种形式进行编码: 记录型[35 ] 和多元型[66 ] .这两种类型之间没有严格的划分并且可以相互转化, 某些数据既可以作为记录型也可以作为序列型.一般来说, 记录型样本编码侧重更高的编码精度, 保留更多信息; 而序列型样本编码侧重更快的运算速度, 占用更少的计算资源.具体编码方式如下. ...
... (3) 更好的预处理方法.对于第5.1节中的第二个问题, 在输入超维计算前提前使用一些高效的预处理方法是有效的.预处理可以实现减少数据量, 去除冗余信息, 保留核心特征数据等功能, 这也对提高最终的识别准确率有一定的帮助.对于图像等数据而言, 可以使用类似包络提取[26 , 35 ] 、投影变换、稀疏表示[73 ] 、主成分分析等特征提取方法将原始数据转化为向量形式或降低待处理数据量后再进行编码.甚至可以如文献[74 ]中通过哈希神经网络产生图像的高维表示, 直接作为样本超维向量输入超维计算进行训练和测试, 也可以取得良好的识别效果.但值得注意和思考的是, 如何在通过额外计算量以完成预处理和保持超维计算的轻量化快速认知模型之间保持平衡. ...
Hyperdimensional computing with local binary patterns: one-shot learning of seizure onset and identification of ictogenic brain regions using short-time iEEG recordings
2
2019
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
... (1) 最高识别准确率一般低于基于神经网络的连接主义模型.虽然在计算资源有限的平台中, 在相同的训练时间, 或在可用样本数量较少等情况下, 超维计算的准确率可以接近甚至高于神经网络及其他分类识别算法.但是, 在不考虑计算成本的情况下, 除了例如文献[36 ]研究的癫痫病发作检测和文献[71 ]研究的乳腺癌识别等部分应用领域外, 超维计算的识别准确率一般低于连接主义算法, 且由于超维计算的模型和参数较为简单, 在相对固定的模型框架下准确率也相对固定, 最高准确率难以进一步提升.因此, 文献[27 ]将超维计算的识别准确率称为是一种可接受的准确率. ...
1
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
MulTa-HDC: a multi-task learning framework for hyperdimensional computing
1
2021
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
Sequence prediction with sparse distributed hyperdimensional coding applied to the analysis of mobile phone use patterns
1
2015
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
Modeling dependencies in multiple parallel data streams with hyperdimensional computing
0
2014
1
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
1
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
3
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
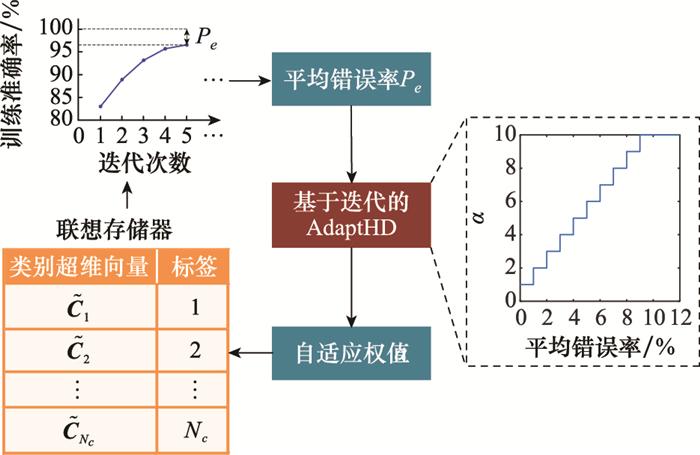
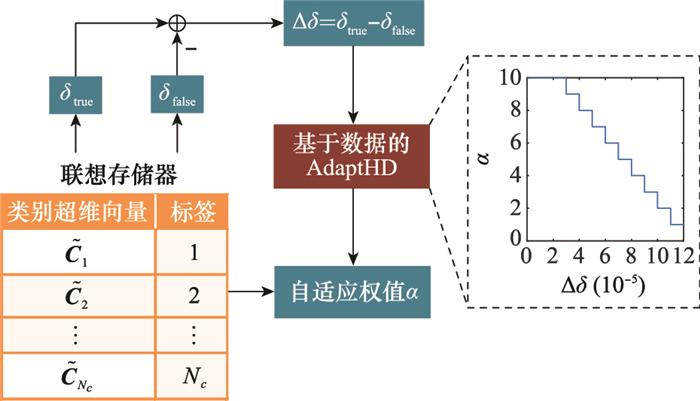
... 为解决上述问题, Imani等人又进一步提出了一种基于超维计算的自适应学习方法(adaptive learning approach based on hyperdimensional computing, AdaptHD)[43 ] .对于第一个问题, AdaptHD不再对使用记录型样本编码得到的样本超维向量和训练得到的类别超维向量进行标准化处理, 保留加法运算产生的原始整数类型超维向量, 即$\tilde{\boldsymbol{R}}$ i $\tilde{\boldsymbol{C}}$ k α 与$\tilde{\boldsymbol{R}}$ i
... 由图 10 和图 11 可以看出, 对于方法1和方法2中α 的取值, 文献[43 ]均采用阶梯式方法, 即将浮点数形式的P e δ 划分为多个区间, 每个区间中使用对应的整数α 取值.该方法具有良好的自适应效果, 在训练样本与训练得到的模型有较大差异时可以明显加速训练准确率的收敛, 提升最终的模型精度与识别准确率. ...
High-dimensional computing as a nanoscalable paradigm
1
2017
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
1
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
Hardware optimizations of dense binary hyperdimensional computing: remateria-lization of hypervectors, binarized bundling, and combinational associative memory
1
2019
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
Accelerating hyperdimensional computing on FPGAs by exploiting computational reuse
1
2020
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
1
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
1
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
In-memory hyperdimensional computing
1
2020
... 超维计算已经在语音识别[29 ] 、语言识别[30 -31 ] 、手写数字识别[32 ] 、合成孔径雷达(synthetic aperture radar, SAR)图像识别[33 ] 、人体姿态识别[26 ] 、生物信号处理[34 -36 ] 、脱氧核糖核酸(deoxyribonucleic acid, DNA)模式匹配[37 ] 、多任务学习[38 ] 、多传感器信息融合[39 -41 ] 和脑机接口[42 ] 等诸多领域得到了很好的应用.特别是在计算资源严格受限的设备上, 例如树莓派[43 ] (raspberry pi, RPi)、特定应用集成电路[44 -45 ] (application specific integrated circuit, ASIC)、现场可编程门阵列[46 -47 ] (field programmable gate array, FPGA)、可变电阻式存储器[48 -49 ] (resistive random-access memory, ReRAM)和相变存储器[50 ] (phase change memory, PCM), 超维计算的优势将更加突出. ...
Neural networks and physical systems with emergent collective computational abilities
1
1982
... 通过压缩函数可以将线性相关矩阵存储器算法中使用的输出向量转化为点吸引子的形式, 实现模型的非线性化.著名的Hopfield网络[51 ] 采用的就是这种方式, 其核心功能是将残缺输入数据通过联想关联重建为完整数据, 具有较好的识别性能和鲁棒性.后续发展为玻尔兹曼机[52 ] 和深度置信网络[53 ] (deep belief network, DBN), 对人工智能领域产生了深远影响.然而, Hopfield网络的存储容量是有限的.例如, 具有N 个神经元的二进制Hopfield网络, 其最大可存储模式为2N [54 ] 围绕联想存储器展开的工作基础上, Kanerva[17 ] 在1988年提出了稀疏分布式存储理论, 通过引入随机权值的方式, 使用固定尺寸的权重矩阵就可以构造无限容量的联想存储器系统, 这也被认为是超维计算存储结构的直接理论雏形之一. ...
A learning algorithm for Boltzmann machines
1
1985
... 通过压缩函数可以将线性相关矩阵存储器算法中使用的输出向量转化为点吸引子的形式, 实现模型的非线性化.著名的Hopfield网络[51 ] 采用的就是这种方式, 其核心功能是将残缺输入数据通过联想关联重建为完整数据, 具有较好的识别性能和鲁棒性.后续发展为玻尔兹曼机[52 ] 和深度置信网络[53 ] (deep belief network, DBN), 对人工智能领域产生了深远影响.然而, Hopfield网络的存储容量是有限的.例如, 具有N 个神经元的二进制Hopfield网络, 其最大可存储模式为2N [54 ] 围绕联想存储器展开的工作基础上, Kanerva[17 ] 在1988年提出了稀疏分布式存储理论, 通过引入随机权值的方式, 使用固定尺寸的权重矩阵就可以构造无限容量的联想存储器系统, 这也被认为是超维计算存储结构的直接理论雏形之一. ...
A fast learning algorithm for deep belief nets
1
2006
... 通过压缩函数可以将线性相关矩阵存储器算法中使用的输出向量转化为点吸引子的形式, 实现模型的非线性化.著名的Hopfield网络[51 ] 采用的就是这种方式, 其核心功能是将残缺输入数据通过联想关联重建为完整数据, 具有较好的识别性能和鲁棒性.后续发展为玻尔兹曼机[52 ] 和深度置信网络[53 ] (deep belief network, DBN), 对人工智能领域产生了深远影响.然而, Hopfield网络的存储容量是有限的.例如, 具有N 个神经元的二进制Hopfield网络, 其最大可存储模式为2N [54 ] 围绕联想存储器展开的工作基础上, Kanerva[17 ] 在1988年提出了稀疏分布式存储理论, 通过引入随机权值的方式, 使用固定尺寸的权重矩阵就可以构造无限容量的联想存储器系统, 这也被认为是超维计算存储结构的直接理论雏形之一. ...
1
2014
... 通过压缩函数可以将线性相关矩阵存储器算法中使用的输出向量转化为点吸引子的形式, 实现模型的非线性化.著名的Hopfield网络[51 ] 采用的就是这种方式, 其核心功能是将残缺输入数据通过联想关联重建为完整数据, 具有较好的识别性能和鲁棒性.后续发展为玻尔兹曼机[52 ] 和深度置信网络[53 ] (deep belief network, DBN), 对人工智能领域产生了深远影响.然而, Hopfield网络的存储容量是有限的.例如, 具有N 个神经元的二进制Hopfield网络, 其最大可存储模式为2N [54 ] 围绕联想存储器展开的工作基础上, Kanerva[17 ] 在1988年提出了稀疏分布式存储理论, 通过引入随机权值的方式, 使用固定尺寸的权重矩阵就可以构造无限容量的联想存储器系统, 这也被认为是超维计算存储结构的直接理论雏形之一. ...
1
1969
... 同时期中, 神经网络等连接主义模型也在感知机之后逐渐发展.1969年, Minsky等人[55 ] 在对感知机的分析中, 提出两大限制连接主义模型发展的缺陷: ①基本感知机无法处理异或回路; ②当时有限的计算机计算能力不足以完成大型多层神经网络的训练.1974年, Werbos首次提出了使用误差反向传播[56 ] 训练神经网络的方法, 有效解决了感知机无法处理异或回路的问题.1986年, Rumelhart等人[57 ] 将反向传播算法推广至多层神经网络, 但是由于计算机性能限制, 仍然难以实现网络的训练和计算.卷积、池化等目前连接主义人工智能算法中的常用概念在当时也被Fukushima[5 ] 引入, 以实现更好的特征提取和减少运算量的效果, 陆续诞生了如LeCun等人在1989年提出的使用反向传播进行训练的卷积神经网络[58 ] 等经典模型. ...
Backpropagation through time: what it does and how to do it
1
1990
... 同时期中, 神经网络等连接主义模型也在感知机之后逐渐发展.1969年, Minsky等人[55 ] 在对感知机的分析中, 提出两大限制连接主义模型发展的缺陷: ①基本感知机无法处理异或回路; ②当时有限的计算机计算能力不足以完成大型多层神经网络的训练.1974年, Werbos首次提出了使用误差反向传播[56 ] 训练神经网络的方法, 有效解决了感知机无法处理异或回路的问题.1986年, Rumelhart等人[57 ] 将反向传播算法推广至多层神经网络, 但是由于计算机性能限制, 仍然难以实现网络的训练和计算.卷积、池化等目前连接主义人工智能算法中的常用概念在当时也被Fukushima[5 ] 引入, 以实现更好的特征提取和减少运算量的效果, 陆续诞生了如LeCun等人在1989年提出的使用反向传播进行训练的卷积神经网络[58 ] 等经典模型. ...
Learning representations by back-propagating errors
1
1986
... 同时期中, 神经网络等连接主义模型也在感知机之后逐渐发展.1969年, Minsky等人[55 ] 在对感知机的分析中, 提出两大限制连接主义模型发展的缺陷: ①基本感知机无法处理异或回路; ②当时有限的计算机计算能力不足以完成大型多层神经网络的训练.1974年, Werbos首次提出了使用误差反向传播[56 ] 训练神经网络的方法, 有效解决了感知机无法处理异或回路的问题.1986年, Rumelhart等人[57 ] 将反向传播算法推广至多层神经网络, 但是由于计算机性能限制, 仍然难以实现网络的训练和计算.卷积、池化等目前连接主义人工智能算法中的常用概念在当时也被Fukushima[5 ] 引入, 以实现更好的特征提取和减少运算量的效果, 陆续诞生了如LeCun等人在1989年提出的使用反向传播进行训练的卷积神经网络[58 ] 等经典模型. ...
Backpropagation applied to handwritten zip code recognition
1
1989
... 同时期中, 神经网络等连接主义模型也在感知机之后逐渐发展.1969年, Minsky等人[55 ] 在对感知机的分析中, 提出两大限制连接主义模型发展的缺陷: ①基本感知机无法处理异或回路; ②当时有限的计算机计算能力不足以完成大型多层神经网络的训练.1974年, Werbos首次提出了使用误差反向传播[56 ] 训练神经网络的方法, 有效解决了感知机无法处理异或回路的问题.1986年, Rumelhart等人[57 ] 将反向传播算法推广至多层神经网络, 但是由于计算机性能限制, 仍然难以实现网络的训练和计算.卷积、池化等目前连接主义人工智能算法中的常用概念在当时也被Fukushima[5 ] 引入, 以实现更好的特征提取和减少运算量的效果, 陆续诞生了如LeCun等人在1989年提出的使用反向传播进行训练的卷积神经网络[58 ] 等经典模型. ...
Mapping part-whole hierarchies into connectionist networks
1
1990
... 为解决当时多层神经网络难以训练的问题, Hinton[59 ] 在1990年指出, 神经网络在处理层次化结构的信息时必须简化其模式表示方法, 提出用简化表示来表征部分-整体结构.简化描述框架中要求设计一些向量, 每个向量作为一部分一起组成一个整体, 并被压缩成与原始向量相同维度的单个向量, 这个简化后的向量可以作为表示更大整体的一部分.同时, 缩减必须是可逆的, 才能在部分-整体层次结构中双向移动, 但该文献中未给出具体的实现方法.Smolensky[60 ] 提出了一种分布式表示方法, 称为张量积表示.这种方法通过外积运算实现变量与其对应数值的绑定, 其特性满足了简化描述中所期望达到的部分性质.例如, 张量积表示通过简化融合, 将整体和部分的局部特殊情况添加至已有的结构化数据表示中构成一个整体, 允许从简单的表示递归构造复杂的表示等.张量运算在之后也成为连接主义模型的重要基础之一. ...
Tensor product variable binding and the representation of symbolic structures in connectionist systems
1
1990
... 为解决当时多层神经网络难以训练的问题, Hinton[59 ] 在1990年指出, 神经网络在处理层次化结构的信息时必须简化其模式表示方法, 提出用简化表示来表征部分-整体结构.简化描述框架中要求设计一些向量, 每个向量作为一部分一起组成一个整体, 并被压缩成与原始向量相同维度的单个向量, 这个简化后的向量可以作为表示更大整体的一部分.同时, 缩减必须是可逆的, 才能在部分-整体层次结构中双向移动, 但该文献中未给出具体的实现方法.Smolensky[60 ] 提出了一种分布式表示方法, 称为张量积表示.这种方法通过外积运算实现变量与其对应数值的绑定, 其特性满足了简化描述中所期望达到的部分性质.例如, 张量积表示通过简化融合, 将整体和部分的局部特殊情况添加至已有的结构化数据表示中构成一个整体, 允许从简单的表示递归构造复杂的表示等.张量运算在之后也成为连接主义模型的重要基础之一. ...
Holographic reduced representations
1
1995
... 但是, 张量积是以增加表示的尺寸为代价将低阶的信息带至高阶中, 没有实现简化的本质目的.这一问题可以由Plate在1995年提出的全息简化表示[61 ] (holographic reduced representation, HRR)解决.在HRR中, 通过循环卷积的思想实现简化描述: 两个n 维实向量在经过元素级的加法、乘法、循环移位运算后仍然得到一个n 维实向量, 这个实向量将包含由张量积得到的n ×n 矩阵中的所有元素.以HRR为基础, 使用不同的数据类型又衍生出了Kanerva提出的飞溅码[62 ] 、Gayler提出的一般化双极飞溅码[63 ] 等编码方式, 但核心原理基本类似.2003年, 经过补充完善, Plate全面阐述了全息简化表示理论[64 ] , 对于复向量等各类情况也同样适用.通过全息简化表示, 可以实现对各类组合结构的编码和解码, 其中的有关概念与超维计算已经非常相似, 基本奠定了超维计算的核心思想. ...
1
... 但是, 张量积是以增加表示的尺寸为代价将低阶的信息带至高阶中, 没有实现简化的本质目的.这一问题可以由Plate在1995年提出的全息简化表示[61 ] (holographic reduced representation, HRR)解决.在HRR中, 通过循环卷积的思想实现简化描述: 两个n 维实向量在经过元素级的加法、乘法、循环移位运算后仍然得到一个n 维实向量, 这个实向量将包含由张量积得到的n ×n 矩阵中的所有元素.以HRR为基础, 使用不同的数据类型又衍生出了Kanerva提出的飞溅码[62 ] 、Gayler提出的一般化双极飞溅码[63 ] 等编码方式, 但核心原理基本类似.2003年, 经过补充完善, Plate全面阐述了全息简化表示理论[64 ] , 对于复向量等各类情况也同样适用.通过全息简化表示, 可以实现对各类组合结构的编码和解码, 其中的有关概念与超维计算已经非常相似, 基本奠定了超维计算的核心思想. ...
1
... 但是, 张量积是以增加表示的尺寸为代价将低阶的信息带至高阶中, 没有实现简化的本质目的.这一问题可以由Plate在1995年提出的全息简化表示[61 ] (holographic reduced representation, HRR)解决.在HRR中, 通过循环卷积的思想实现简化描述: 两个n 维实向量在经过元素级的加法、乘法、循环移位运算后仍然得到一个n 维实向量, 这个实向量将包含由张量积得到的n ×n 矩阵中的所有元素.以HRR为基础, 使用不同的数据类型又衍生出了Kanerva提出的飞溅码[62 ] 、Gayler提出的一般化双极飞溅码[63 ] 等编码方式, 但核心原理基本类似.2003年, 经过补充完善, Plate全面阐述了全息简化表示理论[64 ] , 对于复向量等各类情况也同样适用.通过全息简化表示, 可以实现对各类组合结构的编码和解码, 其中的有关概念与超维计算已经非常相似, 基本奠定了超维计算的核心思想. ...
1
2003
... 但是, 张量积是以增加表示的尺寸为代价将低阶的信息带至高阶中, 没有实现简化的本质目的.这一问题可以由Plate在1995年提出的全息简化表示[61 ] (holographic reduced representation, HRR)解决.在HRR中, 通过循环卷积的思想实现简化描述: 两个n 维实向量在经过元素级的加法、乘法、循环移位运算后仍然得到一个n 维实向量, 这个实向量将包含由张量积得到的n ×n 矩阵中的所有元素.以HRR为基础, 使用不同的数据类型又衍生出了Kanerva提出的飞溅码[62 ] 、Gayler提出的一般化双极飞溅码[63 ] 等编码方式, 但核心原理基本类似.2003年, 经过补充完善, Plate全面阐述了全息简化表示理论[64 ] , 对于复向量等各类情况也同样适用.通过全息简化表示, 可以实现对各类组合结构的编码和解码, 其中的有关概念与超维计算已经非常相似, 基本奠定了超维计算的核心思想. ...
1
... 2008年, Levy[65 ] 将以高维、分布式数据表示作为识别基础的计算模型统称为矢量符号架构(vector symbolic architectures, VSA), 涵盖了全息简化表示、飞溅码等诸多理论.矢量符号架构作为一种新型人工智能架构, 提供了一种系统的方式来生成和操作各类信息的高维表示来完成认知操作.超维计算是矢量符号架构等早期模型的继承者, 在硬件效率方面有着很强的附加优势[16 ] .超维计算中的大量概念和思想也同样适用于矢量符号架构模型, 因此矢量符号架构也常被作为超维计算的别称之一. ...
1
... 现有的样本编码方法中, 主要将数据按两种形式进行编码: 记录型[35 ] 和多元型[66 ] .这两种类型之间没有严格的划分并且可以相互转化, 某些数据既可以作为记录型也可以作为序列型.一般来说, 记录型样本编码侧重更高的编码精度, 保留更多信息; 而序列型样本编码侧重更快的运算速度, 占用更少的计算资源.具体编码方式如下. ...
1
... 文献[22 ]对欧洲21国语言进行了分类, 基于Wortschatz语料库[67 ] 中约一百万字节的文本训练得到每个国家语言的样本超维向量, 使用Europarl语料库[68 ] 中每个国家各1 000个单独句子作为测试样本, 最终的平均识别准确率为96.7%, 以传统机器学习一半的运算成本和能耗实现了仅比传统机器学习方法低1.2%的准确率, 且具有比传统机器学习方法更好的容错率.文献[31 ]将该算法移植至新兴纳米技术集成电路芯片, 实现了20 000个单独句子98%的准确率. ...
1
... 文献[22 ]对欧洲21国语言进行了分类, 基于Wortschatz语料库[67 ] 中约一百万字节的文本训练得到每个国家语言的样本超维向量, 使用Europarl语料库[68 ] 中每个国家各1 000个单独句子作为测试样本, 最终的平均识别准确率为96.7%, 以传统机器学习一半的运算成本和能耗实现了仅比传统机器学习方法低1.2%的准确率, 且具有比传统机器学习方法更好的容错率.文献[31 ]将该算法移植至新兴纳米技术集成电路芯片, 实现了20 000个单独句子98%的准确率. ...
Holographic graph neuron: a bioinspired architecture for pattern processing
3
2016
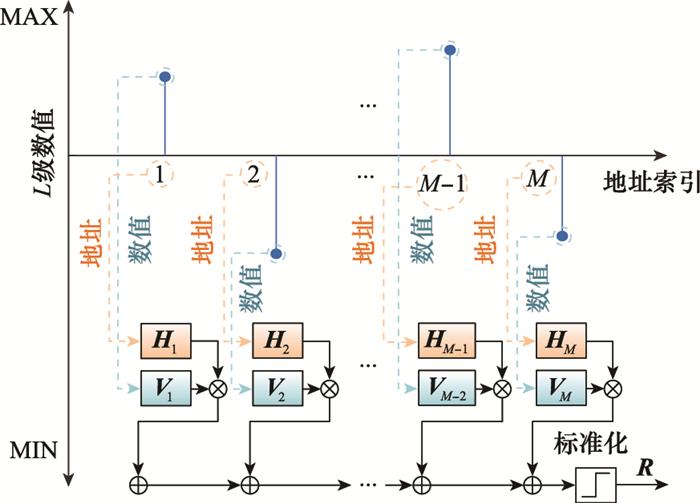
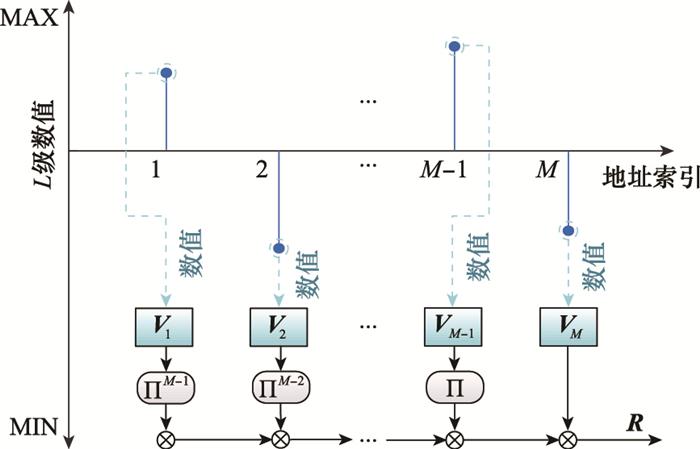
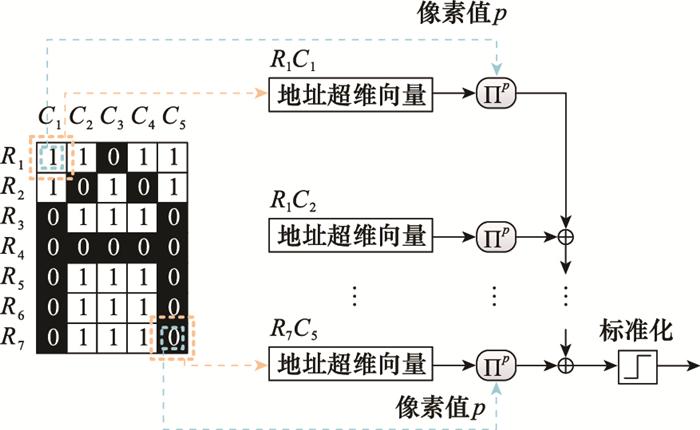
... 目前, 超维计算直接识别图像的研究仍在起步阶段.文献[69 ]将超维计算应用于尺寸为7×5像素的小型黑白字母图像的识别, 其编码方式如图 15 所示. ...
... 首先, 生成35个相互独立且正交的地址超维向量代表每个像素的位置, 根据各个位置的像素值是0还是1决定是否使用移位方式实现的排列运算.这种编码方式在文献[69 ]中被称为全息神经元(holographic graph neuron, HoloGN), 该方法在二进制图像中相比生成数值超维向量再进行样本编码的方式更加高效.在此基础上, 文献[69 ]和文献[70 ]进一步讨论了在字母图像失真等情况下超维计算的表现, 通过二进制编码方式实现了优异识别效果并具有很强的鲁棒性, 在14.3%的失真率下仍然可以保持90%左右的识别准确率, 但识别的黑白字母图像尺寸较小且像素值仅有0和1两种取值. ...
... ]中被称为全息神经元(holographic graph neuron, HoloGN), 该方法在二进制图像中相比生成数值超维向量再进行样本编码的方式更加高效.在此基础上, 文献[69 ]和文献[70 ]进一步讨论了在字母图像失真等情况下超维计算的表现, 通过二进制编码方式实现了优异识别效果并具有很强的鲁棒性, 在14.3%的失真率下仍然可以保持90%左右的识别准确率, 但识别的黑白字母图像尺寸较小且像素值仅有0和1两种取值. ...
1
... 首先, 生成35个相互独立且正交的地址超维向量代表每个像素的位置, 根据各个位置的像素值是0还是1决定是否使用移位方式实现的排列运算.这种编码方式在文献[69 ]中被称为全息神经元(holographic graph neuron, HoloGN), 该方法在二进制图像中相比生成数值超维向量再进行样本编码的方式更加高效.在此基础上, 文献[69 ]和文献[70 ]进一步讨论了在字母图像失真等情况下超维计算的表现, 通过二进制编码方式实现了优异识别效果并具有很强的鲁棒性, 在14.3%的失真率下仍然可以保持90%左右的识别准确率, 但识别的黑白字母图像尺寸较小且像素值仅有0和1两种取值. ...
1
... (1) 最高识别准确率一般低于基于神经网络的连接主义模型.虽然在计算资源有限的平台中, 在相同的训练时间, 或在可用样本数量较少等情况下, 超维计算的准确率可以接近甚至高于神经网络及其他分类识别算法.但是, 在不考虑计算成本的情况下, 除了例如文献[36 ]研究的癫痫病发作检测和文献[71 ]研究的乳腺癌识别等部分应用领域外, 超维计算的识别准确率一般低于连接主义算法, 且由于超维计算的模型和参数较为简单, 在相对固定的模型框架下准确率也相对固定, 最高准确率难以进一步提升.因此, 文献[27 ]将超维计算的识别准确率称为是一种可接受的准确率. ...
Classification and recall with binary hyperdimensional computing: tradeoffs in choice of density and mapping characteristics
1
2018
... (1) 更多的应用领域.作为一种新兴类人脑认知模型, 超维计算的最直接发展方向是在更多的应用领域得到部署和应用, 以其高硬件友好性、高鲁棒性、低样本量需求、快速学习过程和模型可解释性等优势特点, 为各研究领域的不同任务提供一种可能的, 甚至是不可替代的新选择.超维计算所能完成的任务不局限于分类识别, 在环境感知、故障诊断、语义凝练、类比推理和逻辑关系表征等诸多方面, 也有着大量模型层面的先天优势[72 ] . ...
1
... (3) 更好的预处理方法.对于第5.1节中的第二个问题, 在输入超维计算前提前使用一些高效的预处理方法是有效的.预处理可以实现减少数据量, 去除冗余信息, 保留核心特征数据等功能, 这也对提高最终的识别准确率有一定的帮助.对于图像等数据而言, 可以使用类似包络提取[26 , 35 ] 、投影变换、稀疏表示[73 ] 、主成分分析等特征提取方法将原始数据转化为向量形式或降低待处理数据量后再进行编码.甚至可以如文献[74 ]中通过哈希神经网络产生图像的高维表示, 直接作为样本超维向量输入超维计算进行训练和测试, 也可以取得良好的识别效果.但值得注意和思考的是, 如何在通过额外计算量以完成预处理和保持超维计算的轻量化快速认知模型之间保持平衡. ...
Symbolic representation and learning with hyperdimensional computing
1
2020
... (3) 更好的预处理方法.对于第5.1节中的第二个问题, 在输入超维计算前提前使用一些高效的预处理方法是有效的.预处理可以实现减少数据量, 去除冗余信息, 保留核心特征数据等功能, 这也对提高最终的识别准确率有一定的帮助.对于图像等数据而言, 可以使用类似包络提取[26 , 35 ] 、投影变换、稀疏表示[73 ] 、主成分分析等特征提取方法将原始数据转化为向量形式或降低待处理数据量后再进行编码.甚至可以如文献[74 ]中通过哈希神经网络产生图像的高维表示, 直接作为样本超维向量输入超维计算进行训练和测试, 也可以取得良好的识别效果.但值得注意和思考的是, 如何在通过额外计算量以完成预处理和保持超维计算的轻量化快速认知模型之间保持平衡. ...
1
... (5) 与其他算法的配合使用.多种算法相互结合, 取长补短, 发挥各自优势, 是目前的热点研究方向之一.上述第三点中将超维计算与预处理方法结合也是其中的一种算法配合方式.同时, 超维计算与其他分类识别算法, 特别是连接主义模型, 在思路上有着相似之处, 例如都利用信息的高维表示作为运算和处理的基本环节.这也意味着在编码、训练、决策等环节, 超维计算均有着和其他算法直接或间接配合使用的可能[75 -78 ] . ...
Density encoding enables resource-efficient randomly connected neural networks
0
2020
Integer echo state networks: efficient reservoir computing for digital hardware
1
2022
... (5) 与其他算法的配合使用.多种算法相互结合, 取长补短, 发挥各自优势, 是目前的热点研究方向之一.上述第三点中将超维计算与预处理方法结合也是其中的一种算法配合方式.同时, 超维计算与其他分类识别算法, 特别是连接主义模型, 在思路上有着相似之处, 例如都利用信息的高维表示作为运算和处理的基本环节.这也意味着在编码、训练、决策等环节, 超维计算均有着和其他算法直接或间接配合使用的可能[75 -78 ] . ...
1
... (6) 相关硬件与芯片设计.随着超维计算的发展, 相关或专用硬件与芯片设计技术也存在着研究与发展的前景[79 -80 ] , 可能仅使用包含大字长算数逻辑单元(arithmetic and logical unit, ALU)的集成电路就可以很好地完成认知与识别任务[81 ] .并行运算设备和硬件加速框架的发展同样有利于超维计算的发展. ...
1
... (6) 相关硬件与芯片设计.随着超维计算的发展, 相关或专用硬件与芯片设计技术也存在着研究与发展的前景[79 -80 ] , 可能仅使用包含大字长算数逻辑单元(arithmetic and logical unit, ALU)的集成电路就可以很好地完成认知与识别任务[81 ] .并行运算设备和硬件加速框架的发展同样有利于超维计算的发展. ...
A programmable hyper-dimensional processor architecture for human-centric IoT
1
2019
... (6) 相关硬件与芯片设计.随着超维计算的发展, 相关或专用硬件与芯片设计技术也存在着研究与发展的前景[79 -80 ] , 可能仅使用包含大字长算数逻辑单元(arithmetic and logical unit, ALU)的集成电路就可以很好地完成认知与识别任务[81 ] .并行运算设备和硬件加速框架的发展同样有利于超维计算的发展. ...