目标检测作为雷达最基本的功能之一, 已受到众多学者的广泛关注。相控阵(phased array, PA)通过调整发射天线之间的相位关系, 控制天线合成波束指向, 具有波束指向灵活、高分辨、高可靠性等优点, 广泛运用于雷达、通信领域^[1]。然而, PA雷达发射天线方向图仅是角度的函数, 即某一角度位置处雷达波束角度聚焦, 而在旁瓣位置处存在较大信噪比(signal-to-noise ratio, SNR)损失。因此, PA雷达在旁瓣区域的目标检测性能急剧下降。频率分集阵列(frequency diverse array, FDA)概念于2006年被提出^[2-3], 已得到了广泛研究。概念上, FDA在发射阵元间引入了一个小的频率增量, 得到一个距离-角度-时间依赖的发射方向图^[4-5], 在接收端经过信号处理后可以增加系统在距离维的自由度。基于FDA的额外距离维自由度, 可以实现目标距离-角度参数联合估计^[6-7]、机载雷达距离模糊杂波抑制^[8-10]、高分宽幅合成孔径雷达成像^[11-13]、干扰抑制^[14-16]、感知雷达目标跟踪^[17-19]等。此外, 文献[20-21]对FDA雷达的概念与原理、FDA雷达技术研究进展及应用等进行了详细的综述, 阐明了它与相控阵相比的优势及应用前景。在目标检测方面, FDA可实现目标距离-角度检测。文献[22]分析了包括FDA、FDA-多输入多输出(multiple input multiple output, MIMO)雷达在内的不同体制雷达的目标检测性能。文献[23]研究了基于FDA-MIMO雷达的低可观测目标检测技术, 充分利用FDA的灵活的自由度实现运动目标参数的高精度测量。考虑到FDA额外的距离信息, 文献[24]考虑了非均匀环境下的FDA-MIMO雷达检测, 并利用了3种优化方法实现主值距离差估计。文献[25]利用FDA的距离自由度解决了存在欺骗式干扰环境的目标检测问题。文献[26]考虑了FDA使用大频率增量时的多普勒扩展问题, 提出了一种FDA雷达主瓣杂波环境下的盲多普勒目标检测算法。文献[27]考虑了无需训练数据的FDA雷达目标检测, 利用结构广义似然比检测基于目标数据实现了对干扰协方差矩阵的估计。但是, 相比传统PA雷达, FDA雷达方向图仅在脉内短时聚焦, 导致了一定的能量损失, 最终降低了雷达目标检测的性能。

基于上述分析, 本文提出一种联合两种模式雷达的PA和FDA双模式雷达模型, 将均匀线阵部分阵元间引入频率增量, 即将均匀线阵分为两部分: 一部分阵元作为PA阵列, 另一部分阵元作为FDA阵列。通过联合利用PA的灵活波束扫描与FDA发射宽覆盖的优势, 能够在保证一定主瓣检测性能的同时实现旁瓣区域目标的检测。设计了PA和FDA双模联合最优检测器, 推导了检测概率和检测SNR。在仿真部分, 仿真分析了PA和FDA双模式雷达模型的发射方向图; 在检测性能方面, 基于检测概率和检测SNR对比了PA和FDA双模联合检测和单一模式检测的性能。

本文结构如下：第1节建立了PA和FDA双模式雷达发射模型, 分析了PA和FDA双模式雷达模型发射方向图特性, 给出了PA和FDA双模式雷达接收信号模型; 第2节设计了PA和FDA双模式雷达联合最优检测器, 推导了检测概率、检测SNR; 第3节, 仿真分析了双模式雷达发射方向图和检测性能, 并与单一模式PA、FDA雷达进行比较; 第4节提出了结论。

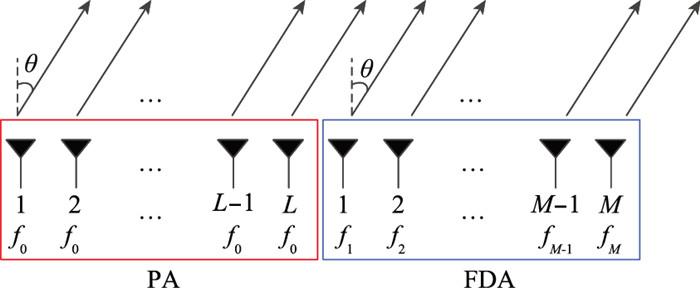
PA和FDA双模式雷达即PA、FDA同时工作的雷达, 本文所指PA和FDA双模式雷达, 是指将天线孔径分为两个独立的部分, 分别发射PA信号和FDA信号。双模式PA和FDA雷达发射信号模型如图 1所示。考虑一个由L+M个全向天线单元组成的均匀线阵, 阵列阵元间距为d, 左边L个阵元组成PA, 右边M个阵元组成FDA。

以左边第一个阵元位置为参考, 阵列发射信号可分为两部分, PA发射信号、FDA第m个阵元发射信号, 可分别表示为

(1) $s^{\mathrm{PA}}(t)=\operatorname{rect}\left(\frac{t}{T_p}\right) \mathit{\Phi}_0(t) \exp \left(\mathrm{j} 2 \pi f_0 t\right)$

(2) $s_m^{\mathrm{FDA}}(t)=\operatorname{rect}\left(\frac{t}{T_p}\right) \mathit{\Phi}_m(t) \exp \left(\mathrm{j} 2 \pi f_m t\right)$

式中: T_p表示脉冲宽度; t∈(0, T_r)表示脉冲重复时间内的时间变量; T_r=1/f_prf表示脉冲重复时间; f₀表示发射信号载频; Φ₀(t)表示PA发射信号包络; Φ_m(t)表示FDA第m个阵元发射信号包络, 且不同载频发射信号波形满足正交性条件, 即$ \int_{T_p} \Phi_m(t) \Phi_{m^{\prime}}^*(t-\tau) \mathrm{dt}=0\left(m, m^{\prime}=0, 1, \cdots, M, m \neq m^{\prime}, \forall \tau\right)$, 其中τ为任意时延, *表示共轭运算; Δf表示频率增量且满足$\Delta f \ll f_0 ; f_m=f_0+(m-1) \Delta f(m=1, 2, \cdots, M) $表示FDA第m个阵元发射信号载频。

考虑空间远场任意距离-角度(R, θ)处单点目标源, 阵列发射信号电磁波在该位置的电场分布可表示为

(3) $\begin{gathered}F=\operatorname{rect}\left(\frac{t-\frac{R}{\mathrm{c}}}{T_p}\right) \cdot \\\left\{\sum\limits_{l=1}^L w_l^* \exp \left\{\mathrm{j} 2 \pi f_0\left(t-\frac{R-(l-1) d \sin \theta}{\mathrm{c}}\right)\right\}+\right. \\\left.\sum\limits_{m=1}^M \exp \left\{\mathrm{j} 2 \pi f_m\left(t-\frac{R-(L+m-1) d \sin \theta}{\mathrm{c}}\right)\right\}\right\}\end{gathered}$

式中: c为光速; w_l表示PA发射端第l个阵元的发射端加权项。即若PA发射端指向空间角度θ_t, PA发射端加权矢量可表示为

(4) $\begin{aligned}& \boldsymbol{w}=\left[w_1, w_2, \cdots, w_L\right]^{\mathrm{T}}= \\& {\left[\begin{array}{c}1 \\\exp \left(\frac{\mathrm{j} 2 \pi f_0 d \sin \theta_t}{\mathrm{c}}\right) \\\vdots \\\exp \left(\frac{\mathrm{j} 2 \pi f_0(L-1) d \sin \theta_t}{\mathrm{c}}\right)\end{array}\right]} \\&\end{aligned}$

由式(3), 某一时刻空间远场位置(R, θ)处的电场强度可表示为

(5) $\begin{gathered}F(t, R, \theta)=\sum\limits_{l=1}^L \exp \left\{\mathrm{j} 2 \pi f_0 \frac{(l-1) d\left(\sin \theta-\sin \theta_t\right)}{\mathrm{c}}\right\}+ \\\exp \left(\mathrm{j} 2 \pi f_0 \frac{L d \sin \theta}{\mathrm{c}}\right) \cdot \\\sum\limits_{m=1}^M \exp \left\{\mathrm { j } 2 \pi \left\{(m-1) \Delta f\left(t-\frac{R}{\mathrm{c}}+\frac{L d \sin \theta}{\mathrm{c}}\right)+\right.\right. \\\left.\left.f_0 \frac{(m-1) d \sin \theta}{\mathrm{c}}\right\}\right\}\end{gathered}$

式(5)中省略了相位中关于阵元序号m的二次项, 即$ \exp \left\{\mathrm{j} 2 \pi(m-1)^2 \Delta f \frac{d \sin \theta}{\mathrm{c}}\right\}$。

当FDA发射信号的频偏满足$\Delta f \ll f_0 $时, 即频率步进量远小于带宽时忽略该项是合理的^{[10, 28-29]}。

由式(5)可以看出, 双模式雷达方向图的幅度和相位响应是时间/距离-角度三维依赖的函数。注意到, 时间和距离实际上是一对共生共存的变量。值得一提的是, 双模式雷达方向图的时间/距离-角度依赖与FDA的时间/距离-角度依赖不完全相同。FDA的时间/距离-角度依赖强调, FDA的主瓣在整个角度空间内覆盖, 即主瓣位置随着距离的不同覆盖在不同的角度; 而时间的概念则是电磁波的传播, 也正是由于时变特性才共生了距离依赖的方向图。对于双模式雷达, 由于PA波束汇聚在空间指向角且同时共存的FDA宽覆盖的距离-角度波束, 雷达波束主瓣在PA发射端指向角位置叠加同时仍存在波束覆盖旁瓣区域。因此, PA和FDA双模式雷达方向图可通过PA发射端加权相位灵活控制叠加主瓣的方向, 并由FDA的频率增量控制旁瓣区域的波束自动扫描, 这种波束覆盖特性将有利于雷达实现特定方向观测的同时实现旁瓣区域目标检测。

考虑阵列全部阵元接收信号, 即接收阵元个数为N=L+M, 第n个阵元接收信号可表示为

(6) $\begin{gathered}y_n=y_n^{\mathrm{PA}}+y_n^{\mathrm{FDA}}=\sum\limits_{l=1}^L\left\{\xi \alpha \operatorname{rect}\left(\frac{t-\tau_0}{T_p}\right) \mathit{\Phi}_0\left(t-\tau_{l, n}^{\mathrm{PA}}\right) \cdot\right. \\\left.w_l^* \exp \left(\mathrm{j} 2 \pi f_0\left(t-\tau_{l, n}^{\mathrm{PA}}\right)\right)\right\}+ \\\sum\limits_{m=1}^M\left\{\xi \alpha \operatorname{rect}\left(\frac{t-\tau_0}{T_p}\right) \mathit{\Phi}_m\left(t-\tau_{m, n}^{\mathrm{FDA}}\right) \cdot\right. \\\left.\exp \left(\mathrm{j} 2 \pi f_m\left(t-\tau_{m, n}^{F \mathrm{FA}}\right)\right)\right\}\end{gathered}$

式中：ξ表示目标复散射系数; α~CN(0, 1)表示通道复正态随机系数; τ₀=2R/c表示目标信号时延;

$\tau_{l, n}^{\mathrm{PA}}=\frac{2 R-(l-1) d \sin \theta-(n-1) d \sin \theta}{\mathrm{c}}$

表示PA的双程时延;

$\tau_{m, n}^{\mathrm{FDA}}=\frac{2 R-(L+m-1) d \sin \theta-(n-1) d \sin \theta}{\mathrm{c}}$

表示FDA的双程时延。

在接收端, 接收信号经过下变频、匹配滤波、数字混频, 信号可表示为PA和FDA接收信号两部分, 即

(7) $y_n^{\mathrm{PA}}=\alpha \beta_1 \exp \left\{\mathrm{j} 2 \pi(n-1) \frac{d \sin \theta}{\lambda_0}\right\}$

(8) $\begin{gathered}y_{m n}^{\mathrm{FDA}} \approx \alpha \beta_2 \exp \left\{\mathrm{j} 2 \pi(n-1) \frac{d \sin \theta}{\lambda_0}\right\} \cdot \\\exp \left\{\mathrm{j} 2 \pi(m-1)\left(-\Delta f \frac{2 R}{\mathrm{c}}+\frac{d \sin \theta}{\lambda_0}\right)\right\}\end{gathered}$

式中: 由于$(M-1) \Delta f / f_0 \ll 1, y_{m n}^{\mathrm{FDA}} $忽略了相位差$\exp \{\mathrm{j} 2 \pi \cdot(m-1) \Delta f L d \sin \theta / c\} $。将PA和FDA进行排列, 可构建双模式雷达信号模型为

(9) $\boldsymbol{y}={ }_\alpha \boldsymbol{v}(R, \theta) \boldsymbol{\beta}+\boldsymbol{n} \in {\bf{C}}^{(M+1) N \times 1}$

式中: $ \boldsymbol{\beta}=\left[\beta_1, \beta_2\right]^{\mathrm{T}} \in \bf{C}^{2 \times 1}, \beta_1=\xi \eta_1$包括PA发射端波束形成项η₁和目标复散射系数ξ, β₂=ξη₂包括FDA发射端相对参考阵元位置导致的相位差η₂和目标复散射系数ξ; v(R, θ)表示双模式雷达联合发射-接收导向矢量。具体地,

(10) $\eta_1=\sum\limits_{l=1}^L \exp \left\{\mathrm{j} 2 \pi(l-1) \frac{d\left(\sin \theta-\sin \theta_0\right)}{\lambda}\right\}$

(11) $\eta_2=\exp \left\{\mathrm{j} 2 \pi \frac{L d \sin \theta}{\lambda}\right\}$

(12) $\boldsymbol{v}(R, \theta)=\operatorname{diag}(1, \boldsymbol{a}(R, \theta)) \otimes \boldsymbol{b}(\theta) \in {\bf{C}}^{(M+1) N \times 2}$

式中: b(θ)表示接收导向矢量; a(R, θ)表示FDA发射端导向矢量。

为了评估双模式雷达检测性能, 首先设计了所提双模式雷达在Neyman-Pearson准则下的最优检测器; 为了分析所提双模式雷达的检测器性能, 分析了最优检测器下的检测概率和检测SNR。

构建如下二元假设检验问题

(13) $\left\{\begin{array}{l}\mathrm{H}_0: \boldsymbol{y}=\boldsymbol{n} \sim \mathrm{CN}(0, \bf{R}) \\\mathrm{H}_1: \boldsymbol{y}=\alpha \boldsymbol{v} \boldsymbol{\beta}+\boldsymbol{n} \sim \mathrm{CN}(\alpha \boldsymbol{v} \boldsymbol{\beta}, \bf{R})\end{array}\right.$

根据Neyman-Pearson准则, 最优检测器为似然比检测器(likelihood ratio test, LRT), 即

(14) $T=\ln \frac{f\left( \boldsymbol{y}\mid {{H}_{1}} \right)}{f\left( \boldsymbol{y}\mid {{H}_{0}} \right)}\underset{{{H}_{0}}}{\overset{{{H}_{1}}}{\mathop{\gtrless }}}\,\varsigma $

式中: $ \varsigma $表示检测阈值; $f\left(\boldsymbol{y} \mid \mathrm{H}_1\right) \text { 和 } f\left(\boldsymbol{y} \mid \mathrm{H}_0\right) $分别表示H₁假设和H₀假设下的观测向量的概率密度函数(probability density function, PDF), 可分别写为

(15) $f\left(\boldsymbol{y} \mid \mathrm{H}_0\right)=c_1^{\prime} \exp \left(-\frac{1}{\sigma_n^2}\|\boldsymbol{y}\|^2\right)$

(16) $\begin{gathered}f\left(\boldsymbol{y} \mid \mathrm{H}_1\right)=\int_0^1 f\left(\boldsymbol{y} \mid \mathrm{H}_1\right) f(\alpha) \mathrm{d} \alpha= \\c_1^{\prime} \exp \left(-\frac{1}{\sigma_n^2}\|\boldsymbol{y}\|^2\right) \cdot \exp \left(-\frac{\left\|\boldsymbol{y}^{\dagger} \boldsymbol{v} \boldsymbol{\beta}\right\|^2}{\sigma_n^2+|\boldsymbol{v} \boldsymbol{\beta}|^2}\right)\end{gathered}$

式中: σ_n²表示噪声功率; $(\cdot)^{\dagger} $表示共轭转置操作；c′₀和c′₁表示与信号参数无关的常数项。将式(15)和式(16)代入式(14), 可得最优检测器为

(17) $T={{\left\| {{\boldsymbol{y}}^{\dagger }}\boldsymbol{v }\boldsymbol{\beta} \right\|}^{2}}\underset{{{H}_{0}}}{\overset{{{H}_{1}}}{\mathop{\gtrless }}}\,\varsigma $

式中: $ y^{\dagger} \boldsymbol{v} \boldsymbol{\beta}=\left\{\begin{array}{l}n, H_0 \\\|\boldsymbol{v} \boldsymbol{\beta}\|^2 \alpha+n, \mathrm{H}_1\end{array}, n \sim \mathrm{CN}\left(0, \sigma_n^2|\boldsymbol{v} \boldsymbol{\beta}|^2\right)\right.$。因此, 最优检测器统计量的分布函数为

(18) $\left\{\begin{array}{l}\frac{\sigma_n^2}{2}\left(\eta_1^2+M\right) N \chi_2^2, \mathrm{H}_0 \\\left(\frac{\rho\left(\eta_1^2 N+M N\right)^2}{2}+\frac{\sigma_n^2}{2}\left(\eta_1^2+M\right) N\right) \chi_2^2, \mathrm{H}_1\end{array}\right.$

式中: ρ=ξ²表示目标复散射系数相关的输入信号功率。根据式(18), 最优检测器的检测概率(probability of detection, PD)、阈值、检测虚警率(probability of false alarm, PFA)可分别表示为

(19) $P_d^{\mathrm{PA}+\mathrm{FDA}}=1-F_{\chi_2^2}\left(\frac{F_{\chi_2^2}^{-1}\left(1-P_{\mathrm{fa}}\right)}{1+\frac{\rho\left(\eta_1^2 N+M N\right)}{\sigma_n^2}}\right)$

(20) $\varsigma^{\mathrm{PA}+\mathrm{FDA}}=\frac{\sigma_n^2}{2}\left(\eta_1^2+M\right) N F_{\chi_2^{-1}}^{-1}\left(1-P_{\mathrm{fa}}\right)$

(21) $P_{\mathrm{fa}}^{\mathrm{PA}+\mathrm{FDA}}=\operatorname{Pr}\left(\chi_2^2>\frac{2 \varsigma}{\sigma_n^2\left(\eta_1^2+M\right) N}\right)$

为了分析比较双模式雷达与PA和FDA的性能, 相似地, PA和FDA雷达最优检测器的PD、阈值、PFA可写为

(22) $P_d^{\mathrm{PA}}=1-F_{\chi_{(2)}^2}\left(\frac{F_{\chi_{(i)}^2}^{-1}\left(1-P_{\mathrm{FA}}\right)}{1+\frac{\rho \eta_{\mathrm{PA}}^2 N^{\mathrm{PA}}}{\sigma_n^2}}\right)$

(23) $P_d^{\mathrm{FDA}}=1-F_{\chi_{(2)}^2}\left(\frac{F_{\chi_{(2)}^2}^{-1}\left(1-P_{\mathrm{FA}}\right)}{1+\frac{\rho M^{\mathrm{FDA}} N^{\mathrm{FDA}}}{\sigma_n^2}}\right)$

(24) $\varsigma^{\mathrm{PA}}=\frac{\sigma_n^2 N^{\mathrm{PA}}}{2} F_{\chi_{(2)}^{-1}}^{-1}\left(1-P_{\mathrm{FA}}\right)$

(25) $\varsigma^{\mathrm{FDA}}=\frac{\sigma_n^2 M^{\mathrm{FDA}} N^{\mathrm{FDA}}}{2} F_{\chi_{(2)}^2}^{-1}\left(1-P_{\mathrm{FA}}\right)$

(26) $P_{\mathrm{fa}}^{\mathrm{PA}}=P\left(\chi_{(2)}^2>\frac{2 \zeta^{\mathrm{PA}}}{\sigma_n^2 N^{\mathrm{PA}}}\right)$

(27) $P_{\mathrm{fa}}^{\mathrm{FDA}}=P\left(\chi_{(2)}^2>\frac{2 \zeta^{\mathrm{FDA}}}{\sigma_n^2 M^{\mathrm{FDA}} N^{\mathrm{FDA}}}\right)$

式中: PA发射、接收阵元个数分别为M^PA和N^PA, FDA发射、接收阵元个数分别为M^FDA和N^FDA。从式(20)、式(24)和式(25)可以看出, 与PA、FDA雷达不同, PA和FDA双模式雷达最优检测阈值与角度相关。

本节分析了不同雷达模式下的检测性能。定义PA、FDA以及PA和FDA双模式雷达波束形成等效SNR:

(28) $\mathrm{SNR}^{\mathrm{PA}} \triangleq \frac{\rho \eta_{\mathrm{PA}}^2 N^{\mathrm{PA}}}{\sigma_n^2}$

(29) $\mathrm{SNR}^{\mathrm{FDA}} \triangleq \frac{\rho M^{\mathrm{FDA}} N^{\mathrm{FDA}}}{\sigma_n^2}$

(30) $\mathrm{SNR}^{\mathrm{PA}+\mathrm{FDA}} \triangleq \frac{\rho\left(\eta_1^2 N+M N\right)}{\sigma_n^2}$

式中: η_PA是关于PA发射阵元个数、目标角度的波束形成项, 可写为

(31) $\eta_{\mathrm{PA}}=\xi \sum\limits_{m=1}^{M^{\mathrm{PA}}} \exp \left\{\mathrm{j} 2 \pi(m-1) \frac{d\left(\sin \theta-\sin \theta_0\right)}{\lambda}\right\}$

雷达PD可重写为

(32) $P_d(i)=1-F_{\chi_2^2}\left(\frac{1}{1+\operatorname{SNR}(i)} F_{\chi_2^2}^{-1}\left(1-P_{\mathrm{fa}}\right)\right)$

式中:

$\begin{gathered}\mathrm{SNR}(i)=\left\{\begin{array}{l}\mathrm{SNR}^{\mathrm{PA}}, i=1 \\\mathrm{SNR}^{\mathrm{FDA}}, i=2 \\\mathrm{SNR}^{\mathrm{PA}+\mathrm{FDA}}, i=3\end{array}\right. \\P_d(i)=\left\{\begin{array}{l}P_d^{\mathrm{PA}}, i=1 \\P_d^{\mathrm{FDA}}, i=2 \\P_d^{\mathrm{PA}+\mathrm{FDA}}, i=3\end{array}\right.\end{gathered}$

显然, 雷达检测概率与波束形成SNR成正比, SNR越大, 检测概率越高。因此, 为了分析不同雷达模式下的检测概率, 下面将分析3种雷达模式下的雷达波束形成等效SNR。

由于波束形成等效SNR与阵列阵元个数相关, 分析了两种阵元数条件下的波束形成等效SNR: ①双模式阵列阵元总数与PA和FDA阵列阵元数的总数相等, 即子阵分析; ② PA阵列阵元数等于FDA阵列阵元数, 等于双模式阵列阵元数, 即全阵分析。3种体制下的波束形成SNR可总结如表 1所示。

表 1中，

(33) $\eta=\xi \sum\limits_{m=1}^N \exp \left\{\mathrm{j} 2 \pi(m-1) \frac{d\left(\sin \theta-\sin \theta_0\right)}{\lambda}\right\}$

对于FDA雷达, 由于发射波束广域覆盖特性, SNR^FDA不随目标角度位置变化。而窄波束PA雷达, 发射能量在某一角度位置汇聚, 即η_PA²与sinθ－sinθ₀有关。因此，PA波束形成等效SNR在远离波束指向的目标处SNR损失较大, 且波束形成等效SNR变化范围为$\left[0, \frac{\rho\left(M^{\mathrm{PA}}\right)^2 N}{\sigma_n^2}\right] $。

本文所提PA和FDA双模式雷达检测器, 由于兼具了两种雷达的发射特性, 目标接收SNR随目标角度位置变化, 且波束形成SNR变化范围为$ \left[\frac{\rho M N}{\sigma_n^2}, \frac{\rho\left(L^2 N+M N\right)}{\sigma_n^2}\right]$。

显然, PA和FDA双模式雷达检测器波束形成等效SNR相对PA雷达变化范围较小。

传统PA雷达在分析目标检测性能时, 考虑目标位于主瓣内。实际搜索阶段中, 在旁瓣区域的目标SNR损失较大, 目标检测概率此时急速下降。与传统雷达不同地, FDA雷达发射波束广域覆盖, 目标检测概率不随目标角度位置变化, 但广域覆盖导致接收SNR降低, 最终降低了检测概率。本文所提PA和FDA双模式雷达, 接收SNR随目标角度位置变化较小, 可在较小SNR损失条件下兼顾旁瓣区域目标检测。

由于检测概率也与虚警概率有关, 本节另外分析了检测性能的另外一个理论度量指标: 检测SNR。根据文献[30], 目标检测SNR可表示为

(34) $\gamma=\frac{\left|\mathrm{E}\left(T \mid \mathrm{H}_1\right)-\mathrm{E}\left(T \mid \mathrm{H}_0\right)\right|^2}{\frac{1}{2}\left[\operatorname{Var}\left(T \mid \mathrm{H}_1\right)+\operatorname{Var}\left(T \mid \mathrm{H}_0\right)\right]}$

实际上, 式(34)代表了检测器区分假设H₁和H₀的能力。根据式(18), 式(34)中各项分别为

(35) $\mathrm{E}\left(T \mid \mathrm{H}_0\right)=\left(\eta_1^2+M\right) N \sigma_n^2$

(36) $\mathrm{E}\left(T \mid \mathrm{H}_1\right)=\rho\left(\eta_1^2 N+M N\right)^2+\left(\eta_1^2+M\right) N \sigma_n^2$

(37) $\operatorname{Var}\left(T \mid \mathrm{H}_0\right)=\left(\eta_1^2+M\right)^2 N^2 \sigma_n^4$

(38) $\operatorname{Var}\left(T \mid \mathrm{H}_1\right)=\left[\rho\left(\eta_1^2 N+M N\right)^2+\left(\eta_1^2+M\right) N \sigma_n^2\right]^2$

目标检测SNR可写为

(39) $\gamma^{\mathrm{PA}+\mathrm{FDA}}=\frac{1}{\left[\frac{1}{2}+\frac{1}{\mathrm{SNR}^{\mathrm{PA}+\mathrm{FDA}}}+\left(\frac{1}{\mathrm{SNR}^{\mathrm{PA}+\mathrm{FDA}}}\right)^2\right]}$

相似地, 可得到PA和FDA目标检测SNR分别为

(40) $\gamma^{\mathrm{PA}}=\frac{1}{\frac{1}{2}+\frac{1}{\mathrm{SNR}^{\mathrm{PA}}}+\left(\frac{1}{\mathrm{SNR}^{\mathrm{PA}}}\right)^2}$

(41) $\gamma^{\mathrm{FDA}}=\frac{1}{\frac{1}{2}+\frac{1}{\mathrm{SNR}^{\mathrm{FDA}}}+\left(\frac{1}{\mathrm{SNR}^{\mathrm{FDA}}}\right)^2}$

显然, 检测SNR实际上是关于波束形成SNR的单调递增函数。因此, 雷达最优检测器检测能力与波束形成SNR成正比。

本节仿真实验仿真对比了PA雷达、FDA雷达及PA和FDA双模式雷达的发射方向图, 分析了3种模式下的雷达最优检测特性, 基本仿真参数如表 2所示。

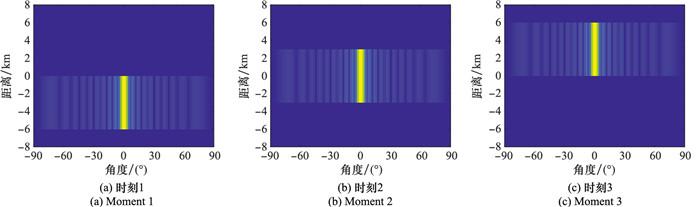
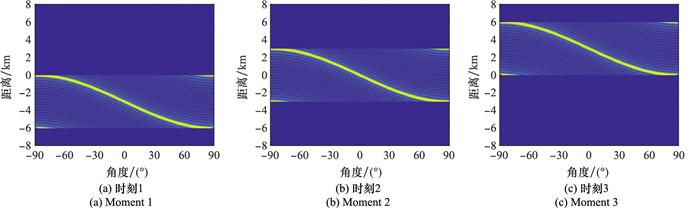
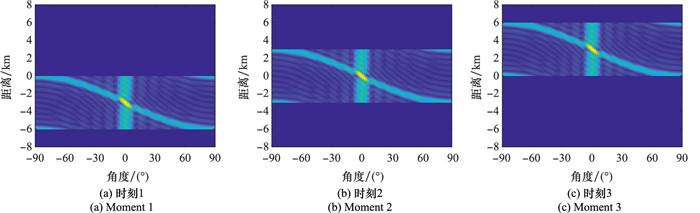
图 2~图 4对比仿真了PA、FDA及PA和FDA双模式雷达在3个不同时刻的发射方向图, 且考虑PA发射端波束指向空间角度0°位置。由于脉冲雷达覆盖距离范围由脉冲宽度决定, 因此3种模式雷达在某一时刻的雷达电磁波都只覆盖了部分空间距离范围。图 2为传统PA雷达在不同时刻的发射方向图, 可以看出PA发射方向图是角度聚焦的, 且随着时间的变化方向图主瓣方向不改变, 即PA方向图是时不变的。图 3为FDA雷达在不同时刻的发射方向图, 可见FDA方向图在角度空间内是全覆盖的, 不同的角度处覆盖在不同的距离位置, 即FDA发射方向图是距离-角度依赖的; 随着时间变化, 空间电磁波向前传播, 对于某一位置处的电磁波, 距离依赖和电磁波传播导致了该位置处电磁波时变, 即FDA方向图的时变性。这就是FDA方向图的时间/距离-角度依赖性。此外, FDA发射电磁波在角度空间内的覆盖范围主要取决于频率偏移量和脉冲宽度之间的关系, 仿真实验中取Δf=1/T_p, 角度空间覆盖范围刚好为整个空间角度范围; 若Δf减小, 则电磁波只覆盖部分角度空间范围。图 4为PA和FDA双模式雷达的发射方向图。由于PA发射方向图聚焦在空间某一角度位置, 双模式雷达发射方向图在角度方向有一个聚焦的波束; 同时由于FDA的距离-角度依赖的广域覆盖特性, 空间电磁波叠加造成双模式雷达在旁瓣区域内实现了全覆盖, 即自动完成了旁瓣扫描。因此, 与传统FDA不完全一致, 双模式雷达不同时刻发射方向图, 存在受PA发射端指向控制的主瓣叠加波束且可同时实现了旁瓣自动扫描, 电磁传播特性与理论分析一致。

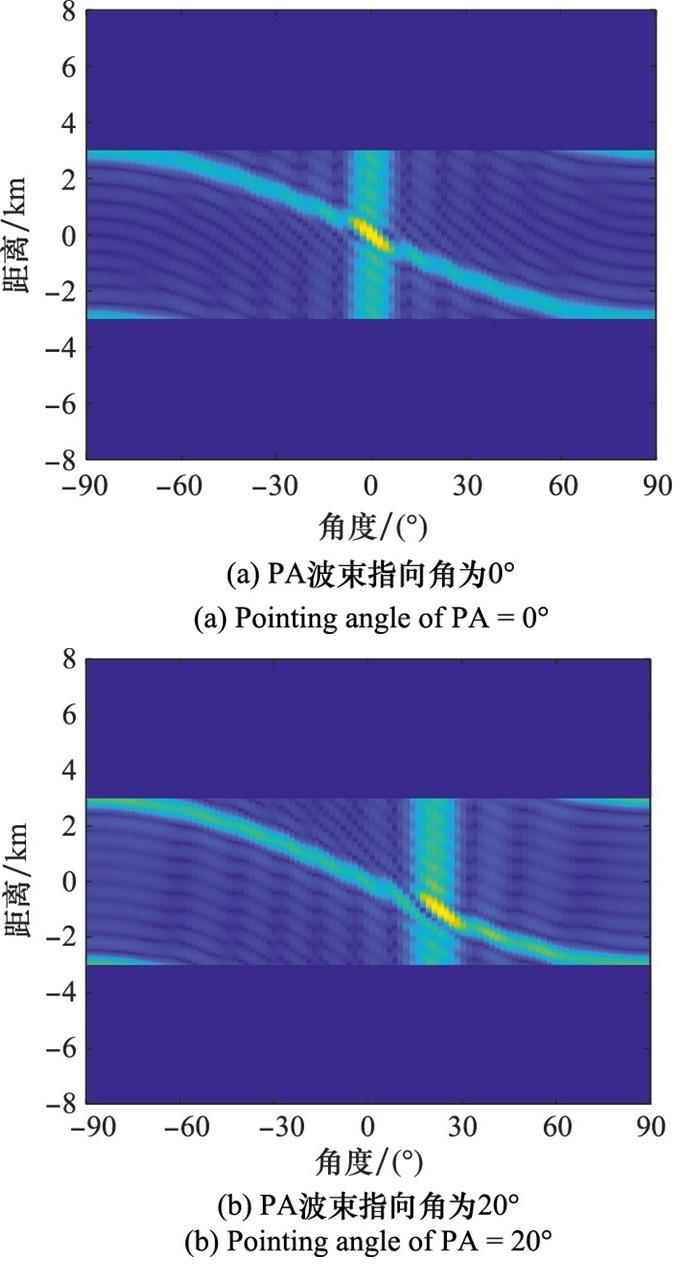
图 5为同一时刻, 经发射端不同角度方向加权后的PA和FDA双模式发射方向图。可以看出, 传统PA发射加权指定了双模式雷达的强式雷达仍可实现整个空间角度自动扫描。因此, PA和FDA双模式雷达下, 相比FDA增加了系统波束的灵活性。实际中, 这种双模式PA和FDA雷达波束特性有利于实现特定方向观测的同时实现旁瓣区域目标搜索。

本节仿真分析了PA、FDA以及PA和FDA双模式雷达的检测特性。由于检测特性与阵列阵元个数相关, 为了分析全面, 本节考虑了两种阵列阵元个数条件。具体地, 本节仿真实验中阵元个数如表 3所示。

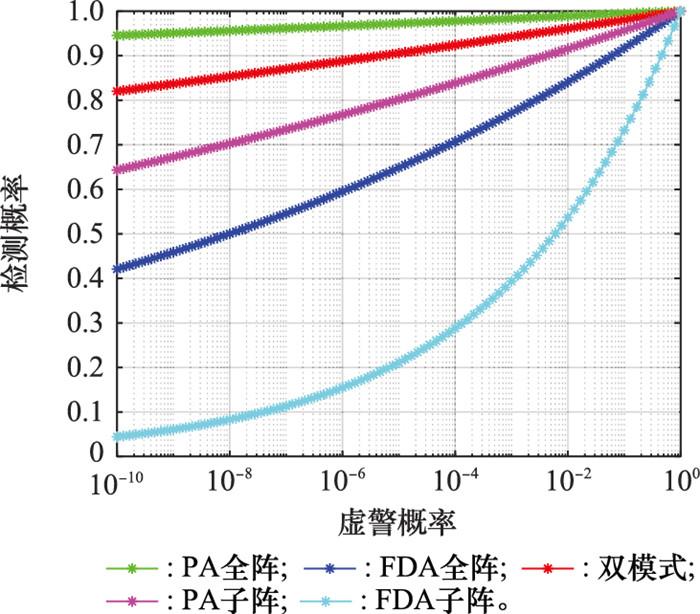
图 6给出了PA、FDA、PA和FDA双模雷达体制在两种阵列阵元条件下的接收器工作特征曲线(receiver operating characteristics, ROC)曲线。考虑目标输入SNR为-10 dB, 即目标散射系数相关的信号功率与噪声功率的比值为-10 dB。由于PA、双模体制下的检测概率与目标角度相关, 本小节考虑远场目标角度为0°, 即考虑主瓣内目标。从图 6中可以看出, 对于主瓣内目标, 由于FDA广域覆盖导致能量分散, 任意虚警率下的PA和FDA双模式雷达检测概率大于子阵FDA、全阵FDA, 检测性能提升明显。由于PA雷达为窄波束, 主瓣内目标接收波束形成等效SNR较高, 且等效SNR与阵元个数成正比。因此, PA和FDA双模式雷达主瓣内目标检测概率高于子阵PA, 但略低于全阵PA。在虚警率为1e-4位置处, PA和FDA双模式雷达相对子阵FDA、全阵FDA检测概率分别提升220.8%、30.6%, 相对子阵PA检测概率提升10.2%, 相对全阵PA检测概率损失5.5%。因此, PA和FDA融合了PA和FDA雷达的优势, 相对FDA极大的提升了主瓣内目标的检测性能。

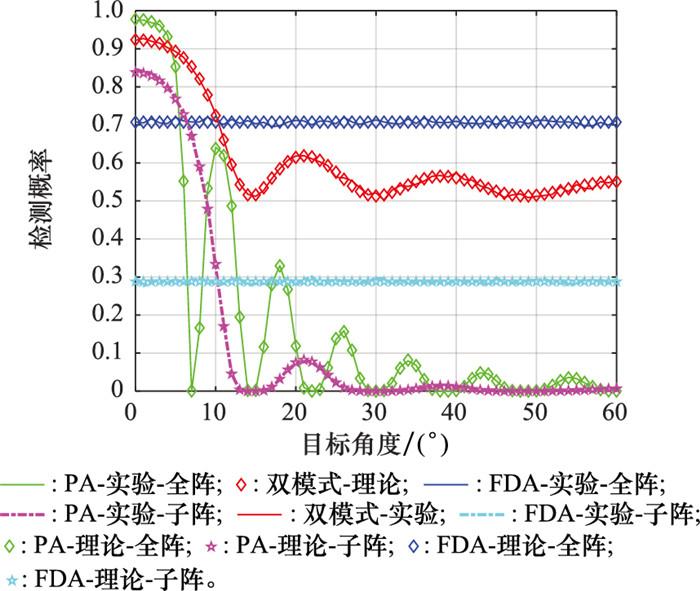
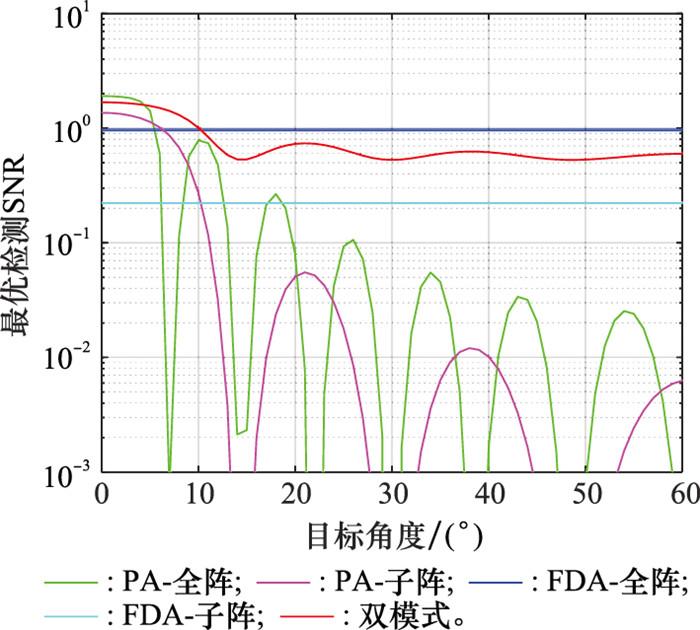
图 7给出了两种阵列条件下3种雷达体制雷达的最优检测概率随目标角度的变化曲线, 考虑目标输入SNR为-10 dB, 检测虚警概率为1e-4。为了证明理论推导的正确性, 分别进行了10 000次和100×PFA次蒙特卡罗实验确定实验阈值和计算检测概率。如图 7所示, 线型表示蒙特卡罗实验结果, 符号表示理论推导结果, 3种体制下的理论结果和实验结果重合, 证明了本文推导检测概率、阈值、虚警概率的理论正确性。且从图 7中可以看出, 由于FDA的广域覆盖特性, FDA在空间任意角度位置处目标波束形成等效SNR相同, 因此空间中不同角度位置处的目标检测概率恒定。对于PA及PA和FDA双模式雷达, 由于不同空间角度位置处目标波束形成等效SNR不同, 目标检测概率随空间角度位置变化。由于PA在旁瓣区域存在较大SNR损失, 因此PA检测概率随角度位置变化较大。对于PA和FDA双模式雷达, 由于融合了FDA的宽覆盖特性, 旁瓣内SNR损失较小, 因此检测概率变化较小。此外, 相对子阵PA、全阵PA以及子阵FDA, PA和FDA双模式雷达在旁瓣内目标检测概率提升明显, 但略低于全阵FDA。具体的, 当目标位于角度25°时, 相对子阵PA、全阵PA以及子阵FDA检测概率提升至少99.86%, 相对全阵FDA性能下降约18.6%。因此, PA和FDA双模式雷达联合目标检测方法相对单一模式雷达不仅可提升雷达在主瓣内的检测性能, 而且可在较小SNR损失下兼顾旁瓣区域目标检测。

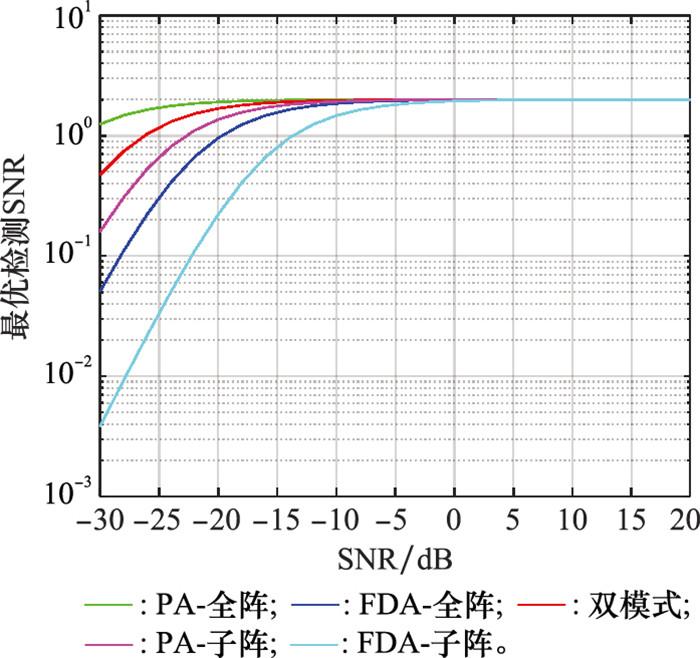
图 8给出了主瓣内角度为0°、距离为45 km位置的目标, 在3种体制下最优检测SNR随输入SNR变化曲线。从图 8中可以看出, 与检测概率分析一致地, PA和FDA双模式雷达在主瓣内检测SNR优于全阵FDA、子阵FDA、子阵PA, 但低于全阵PA, 这是由于检测SNR与接收波束形成SNR相关。当最优检测SNR为1时, PA和FDA双模式雷达相对全阵FDA提升6 dB, 相对子阵FDA提升12 dB, 相对子阵PA提升3 dB, 相对全阵PA下降约5 dB。图 9给出了最优检测SNR与目标角度的关系。与检测概率分析一致, 由于PA在旁瓣存在较大SNR损失, PA雷达检测SNR在旁瓣内很低; 同时, FDA的宽覆盖使得检测SNR不随目标角度改变。PA和FDA双模联合检测相对PA在全空间角度范围内检测概率变化较小, 且旁瓣区域内检测概率显著提升。因此, PA和FDA双模雷达联合检测保证了主瓣内检测性能的同时提高了旁瓣区域目标检测能力。

本文提出了PA和FDA双模式雷达模型。该模型在部分阵列阵元间引入频率增量, 将整个阵列划分为PA阵列、FDA阵列, 将PA和FDA模式同时工作, 获得了较传统FDA雷达更灵活的时间/距离-角度依赖方向图。论文建立了PA和FDA双模分孔径同时工作体制的信号模型, 从理论上建立了最优检测概率和检测SNR与波束形成等效SNR之间的数学关系。PA和FDA双模式雷达发射方向图发挥了PA波束能量聚焦与FDA空间覆盖的优势: 在主瓣方向具有最优的目标检测性能, 在8阵元条件下较FDA单一模式雷达的等效SNR改善达到12.3 dB, 且PA和FDA双模式雷达可以在较小SNR损失的条件下兼顾旁瓣区域的目标检测性能。