0 引言
海杂波背景下检测目标的传统方法是恒虚警率(constant false alarm rate, CFAR)检测算法[3]。该算法基于杂波均匀的假设, 也就是认为每个距离单元的后向散射具有相同的统计分布。然而, 实际处理的海杂波通常是非均匀的, 这导致该算法的检测性能明显下降。
时频联合处理方法可以有效地描述信号频谱分量随时间的变化。常见的时频分析方法有短时傅里叶变换[4](short-time Fourier transform, STFT)、Wigner-Ville分布[5](Wigner-Ville distribution, WVD)和小波变换等。时频分析方法STFT和WVD由于自身固有的缺点, 在抑制海杂波方面仍存在许多难点。小波变换具有良好的时频局部化特性, 常常应用于海杂波背景下的微弱目标检测。小波变换中所用小波函数的选择不是唯一的, 因此如何选择合适的小波函数是一个难点, 而这往往需要通过大量的试验获得[6]。许多学者针对时频信息做了进一步处理, 梁壮等[7]利用时频信息进行奇异值分解的海杂波抑制算法, 通过提取前Q阶信号分量分离目标信号与海杂波, 但是对于阶数的选取会对结果造成影响。左磊等[8]在时频域迭代分解过程中, 利用凸包算法融合特征检测慢速弱目标, 但仍然包含时频处理过程的难点。
小波变换在频域有一个恒定的相对带宽, 称为等Q结构[9], 因此小波变换不能根据信号的振荡属性调整Q值。可调Q因子小波变换(tunable Q-factor wavelet transform, TQWT)可以根据信号的振荡属性高低调整Q值, 通过Q值的选取使可调Q因子小波对具有特定振荡属性的信号实现最优的匹配。对信号进行TQWT处理之后, 在小波子带中呈现出稀疏特性, 因此可以将稀疏表示理论[4]引入海杂波抑制算法的处理过程中。Selesnick[9]首先提出TQWT, 通过选择品质因子Q、过采样率r和分解层数J匹配具有不同振荡属性的信号, 从而实现信号的分离, 适用于存在一个目标的情况。Ng等[10]和Rosenberg等[11]采用基追踪去噪(basis pursuit denoising, BPD)的方法来优化信号的稀疏性, 并通过Ingara实测数据验证该方法的有效性。Farshchian等[12]应用双可调Q小波变换将橡胶充气船和鸟群两种目标从海杂波中分离, 使算法可以适应多个目标存在的情况, 此算法得到进一步应用。潘美燕等[13]提出了基于能量选择的改进TQWT海杂波抑制算法, 该算法具有更好的检测性能, 但是其参数的选取依赖目标信号和海杂波的先验信息。冯云等[14]针对文献[13]进行了改进, 运用形态分量分析法分析得到稀疏系数, 该方法不依赖目标信号和海杂波的先验信息, 但是其选择合适参数的算法复杂度高, 在实际应用中并不适用。
1 TQWT
目标信号具有一定径向速度, 多普勒频谱窄, 振荡特性强, 而海杂波由于海浪的运动导致多普勒频谱展宽, 振荡特性弱。基于此物理机理,利用不同Q因子的小波基函数对海杂波和目标信号进行匹配[13]。由于本文选择的Q因子与海杂波匹配, 而与目标失配, 因此在原始回波与重构海杂波信号的差中目标信号能量占比提高, 可以通过判断结果来确定原始回波中是否存在目标信号。
1.1 模型建立
根据目标信号的有无, 接收的原始回波信号Y有Y0和Y1两种情况:
式中: XT为目标信号;XC为海杂波信号;Xn为噪声分量;Y1为存在目标信号时接收的回波信号; Y0为不存在目标信号时接收的回波信号。由于不存在目标信号, 模型中不存在XT分量。
本文根据海杂波的振荡特性, 选取与之相匹配的品质因子Q、过采样率r和分解层数J对海杂波信号进行重构, 得到海杂波信号的估计值
1.2 TQWT
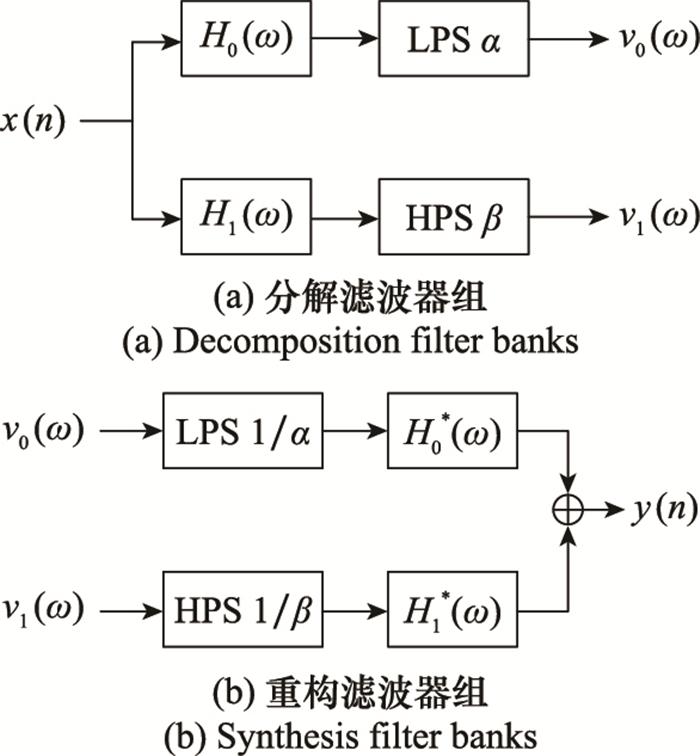
图1
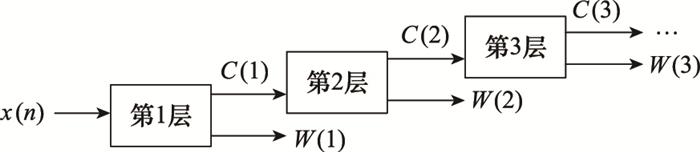
TQWT是由分解滤波器组和重构滤波器组的级联组成。通过多层双通道滤波器组将信号x(n)进行多层分解, 如图 2所示为多层小波分解的实现结构图。将低通小波子带C(j)作为第j+1层双通道滤波器组的输入进行分解, 而高通小波子带W(j)作为第j层小波系数的输出, 其中j为小波分解的层数。
图2
信号重构是分解过程的逆过程, 即TQWT反变换是TQWT变换的逆过程。因此, 重构信号x(n)需要将经过稀疏优化后的低通滤波器的小波系数C(j)和高通滤波器的小波系数W(j)作为第j层的输入, 进行第j层重构。通过多层如图 1(b)所示的重构滤波器组, 就可得到信号x(n)的重构信号y(n)。
1.3 TQWT参数
TQWT是由一系列小波基函数组成的, 小波基函数由过采样率r、品质因子Q和分解层数J这3个参数控制。3个参数的不同组合可以使小波基函数呈现不同的形状和性质, 从而影响TQWT小波系数的稀疏性[16]。
(1) 过采样率r: 由上述分析可知, 双通道滤波器组由α+β因子过采样。如果对双通道滤波器组的低通输出进行无穷迭代以实现小波变换, 则由r=β/(1-α)因子实现过采样, 即所有子带的过采样率总和为r。由文献[16]分析得到, 过采样率r控制小波系数的冗余度, 即如果信号x有N个采样点, 则小波系数的点数为rN。但是当r≈1时, 小波类似于sinc函数, 频域过渡带很窄, 导致时域响应受到限制。为了避免出现此问题, 一般选择r≥3。
(3) 分解层数J: 分解层数过多会造成系数的冗余, 带来巨大的计算量。为了避免此种情况, 通常应限制分解层数。输入信号的长度决定了分解层数, 即需要保证小波长度不低于被分析的信号长度。结合文献[15]的分析, 可以得到J的上限为
式中:
因此选择合适的TQWT参数能够从接收的回波数据中分离出重要的组成部分。换句话说, 选定一组与海杂波最匹配的参数Q、r、J能够从接收的回波信号中准确地估计出海杂波分量。
1.4 稀疏优化
式中: l1-范数项(||·||1)为惩罚项, l2-范数项(||·||2)为保真度项。w是一组小波系数, Φ是与TQWT对应的矩阵, 由品质因子Q、过采样率r和分解层数J这3个参数确定。λ(λ≥0)为正则化参数, 用于调整优化中前后两项的相对重要性。
将BPD应用于目标与海杂波分离的问题, 由式(1)和式(3)得到, 杂波分量的估计值为
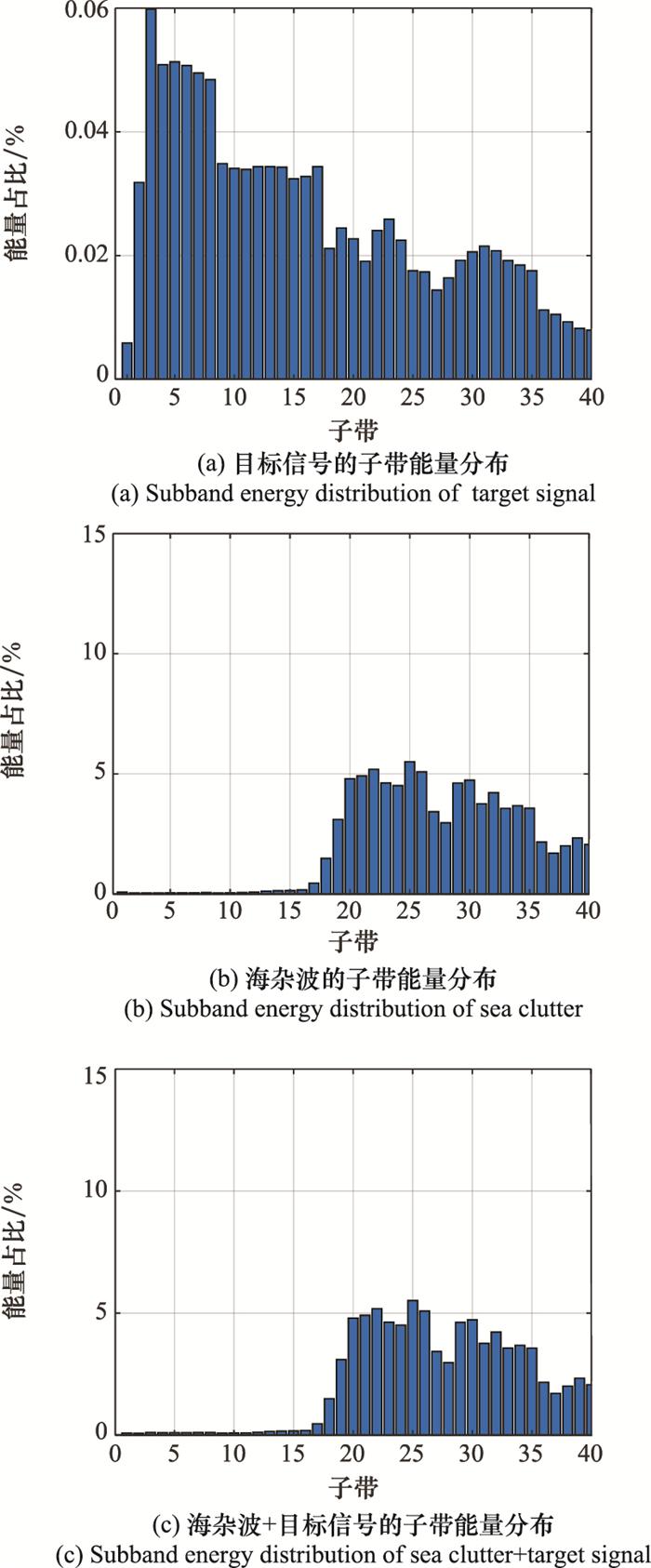
为了验证海杂波经过TQWT之后具有稀疏性, 将实测海杂波数据、仿真目标信号和加入仿真目标信号的海杂波数据分别做TQWT和BPD稀疏优化, 观察各自分解到子带中的小波系数的稀疏性。实测海杂波数据选取某网站的雷达对海探测数据集中的某一个脉冲, 添加仿真目标的参数如表 1所示。将海杂波数据、仿真目标信号和加入仿真目标信号的海杂波数据分别分解到40个小波子带中, 其中子带号从小到大对应频段由高到低。图 3(a)为仿真目标信号的各子带能量分布, 其高频部分子带能量较高, 但整体能量分布比较均匀, 各子带的能量占比相差不大都比较低。由于选取的TQWT参数与仿真目标信号的振荡特性失配, 因此目标信号的各子带不具有稀疏性。图 3(b)为实测海杂波数据的各子带能量分布, 其最后一个小波子带的能量占比明显高于其他子带, 且低频部分子带的能量比较大。由于选取的参数与海杂波的振荡特性相匹配, 因此海杂波信号的各子带具有稀疏性的特征。图 3(c)为加入仿真目标信号的海杂波数据的各子带能量分布, 由于海杂波占主要能量部分, 同时选取的TQWT参数与海杂波相匹配, 因此加入仿真目标信号的海杂波数据的各子带能量分布与海杂波数据的各子带能量分布几乎相同, 都具有稀疏性的特征。
表1 仿真目标参数
Table 1
| 目标编号 | 目标距离单元 | 信杂比/dB | 径向速度/(m·s-1) |
| 1 | 200 | 0 | 1 |
| 2 | 600 | -10 | 3 |
图3
1.5 目标检测
目标检测的过程可以写为
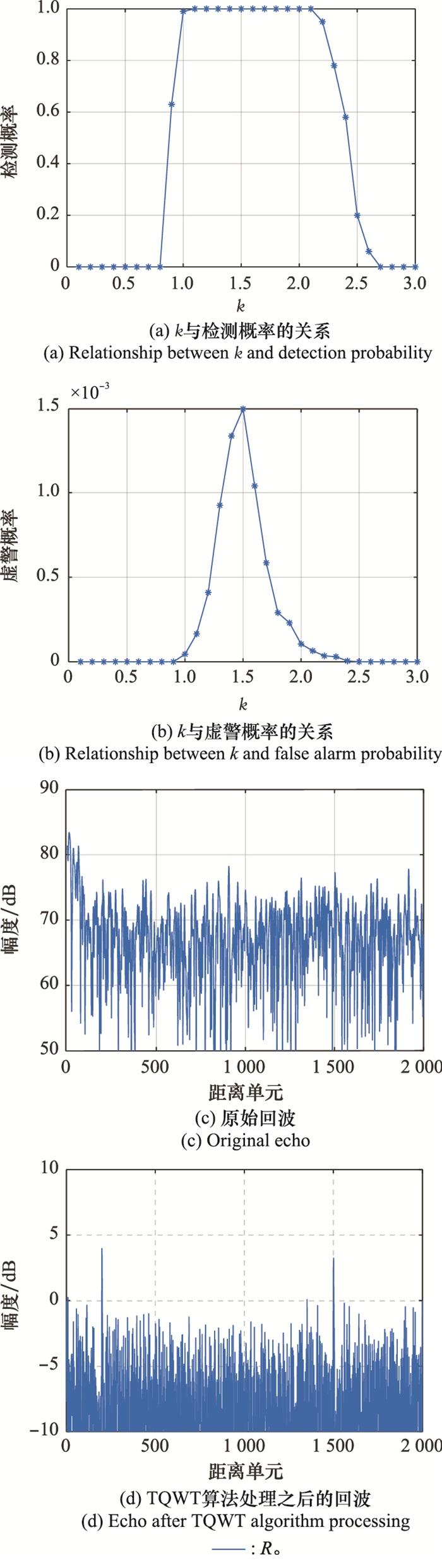
为了确定k的大小, 将仿真目标信号加入实测海杂波数据, 经过TQWT算法处理并做阈值检测, 观察不同的k值确定的阈值检测结果。实测海杂波数据选取某网站的雷达对海探测数据中的某一个脉冲, 添加仿真目标的参数如表 2所示。
图4
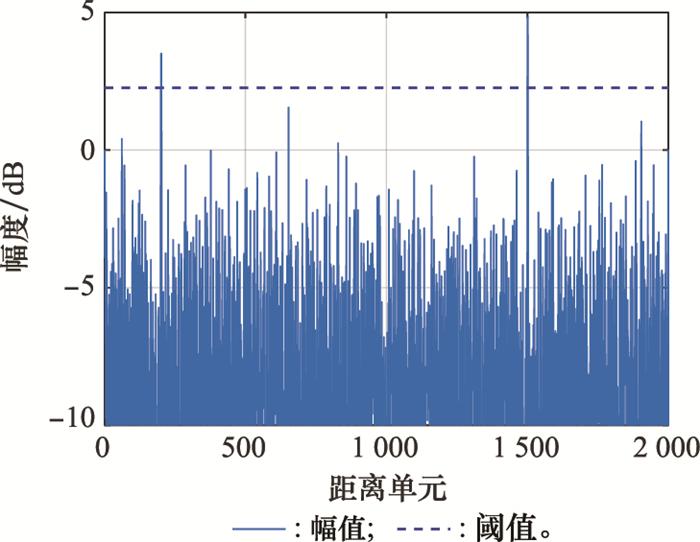
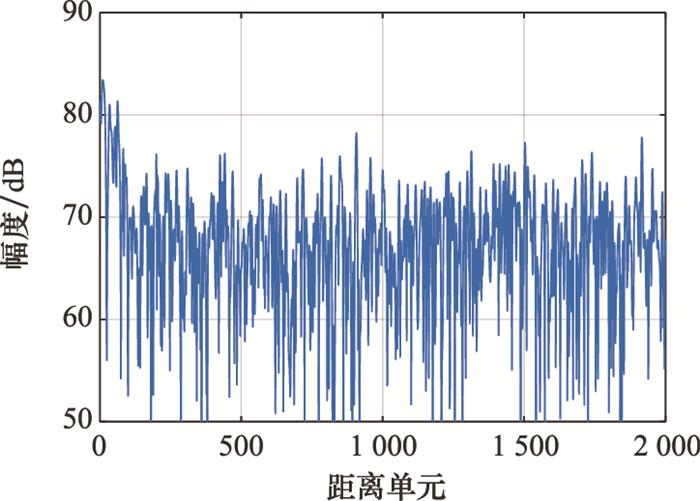
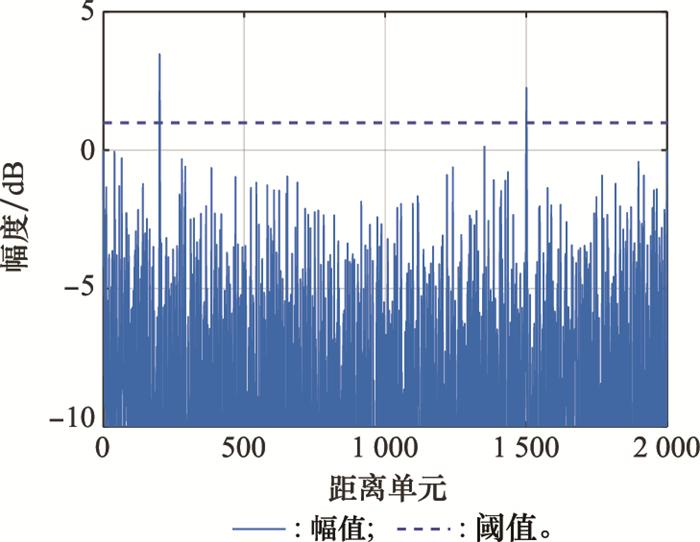
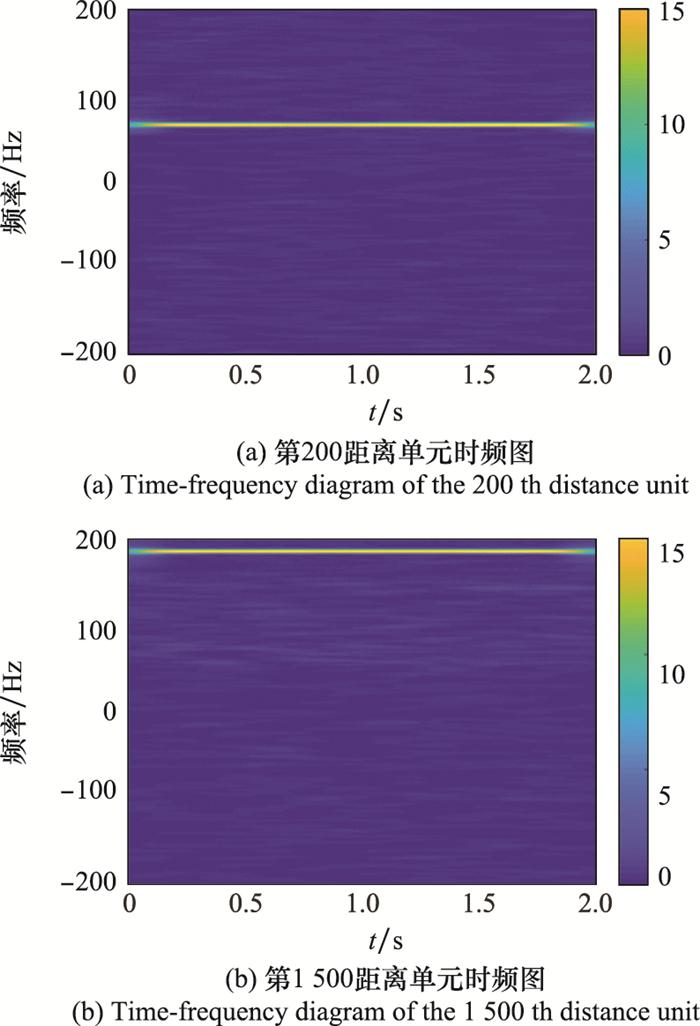
观察图 4(a)和图 4(b)发现, k < 1时, 检测概率和虚警概率都在0附近; 1≤k≤2时, 检测概率为1, 但是其虚警概率较高; k>2时, 虽然虚警概率变化不大, 但是检测概率急速下降。只有k=1时检测概率接近1, 同时虚警概率保持在10-4以下。根据奈曼-皮尔逊准则的思想, k值应该取1, 即阈值为γ=|20lgλmax|。观察图 4(c)和图 4(d), 经过TQWT海杂波抑制算法处理, 第200和第1 500距离单元的目标信号清晰可见。选择不同的阈值进行阈值检测, 其中阈值1为γ=|20lg(0.5λmax)|, 阈值2为γ=|20lgλmax|, 阈值3为λ=|20lg(2λmax)|。当阈值为阈值1和阈值3时, 由于阈值过高, 不能将第200和第1 500距离单元的目标信号全部检测到, 造成漏检。当选择阈值2时, 可以检测到在第200和第1 500距离单元的目标信号, 同时不会将噪声判定为目标信号, 进一步验证了k=1的正确性。
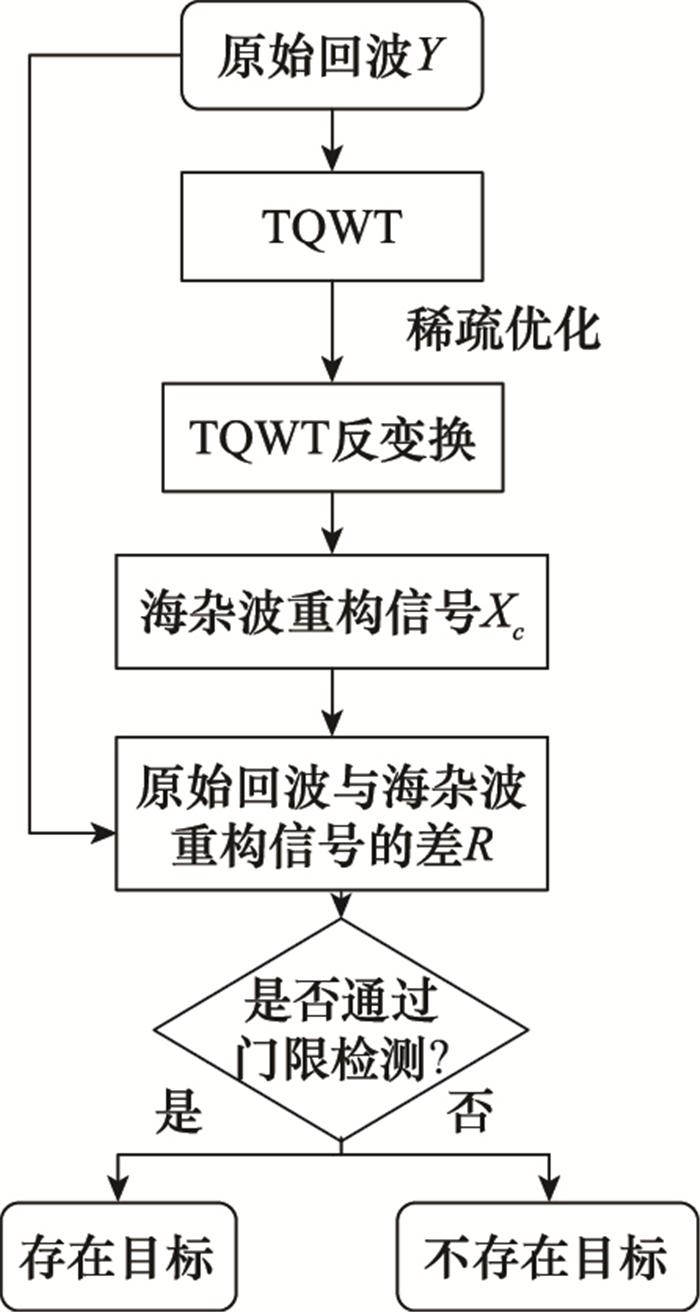
1.6 算法实现及框图
TQWT算法的具体实现步骤如下所示,流程框图如图 5所示。
图5
步骤1 根据海杂波的多普勒运动特性, 选择TQWT参数, 即品质因子Q、过采样率r和分解层数J, 进行TQWT, 将回波信号分解到小波域[17];
步骤2 设置相应的正则化参数λ=||w||2, 对小波系数做BPD稀疏优化处理, 得到最具有稀疏性的一组小波变换系数;
步骤3 通过TQWT反变换进行海杂波重构, 得到海杂波的重构信号
步骤4 将雷达接收回波信号与海杂波重构信号的差R作为检测样本, 与本文提出的自适应阈值λ=|20lgλmax|进行比较, 判断是否存在目标信号。
2 实验及分析
2.1 实验数据
2.2 实验结果及性能分析
将仿真的运动目标信号分别添加到20210106155330_01_staring数据包中的amplitude_complex_T2矩阵和20210105160634_01_staring数据包中的amplitude_complex_T2矩阵中, 分别验证在高海况条件和低海况条件下的海杂波抑制算法的性能。添加仿真目标的参数如表 3所示。
表3 实验目标参数
Table 3
| 目标编号 | 目标距离单元 | 信杂比/dB | 径向速度/(m·s-1) |
| 1 | 200 | -10 | 1 |
| 2 | 1 500 | -20 | 3 |
2.2.1 高海况条件下运动目标的检测
图6
图6
实测数据杂波+仿真目标信号时域分析(Q=8、r=3、J=17)
Fig.6
Time domain analysis of measured data clutter+ simulation target signal (Q=8、r=3、J=17)
图7
图7
实测数据杂波+仿真目标信号时频域分析(Q=8、r=3、J=17)
Fig.7
Time-frequency domain analysis of measured data clutter+simulation target signal (Q=8、r=3、J=17)
图8
图8
实测数据杂波+仿真目标信号TQWT抑制时域分析(Q=8、r=3、J=17)
Fig.8
Time domain analysis by TQWT suppression of measured data clutter+simulation target signal (Q=8、r=3、J=17)
图9
图9
实测数据杂波+仿真目标信号TQWT抑制时频域分析(Q=8、r=3、J=17)
Fig.9
Time-frequency domain analysis by TQWT suppression measured data clutter+simulation target signal (Q=8、r=3、J=17)
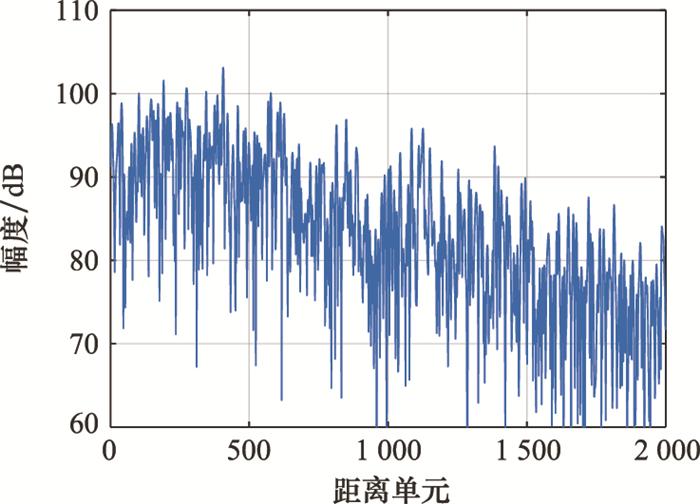
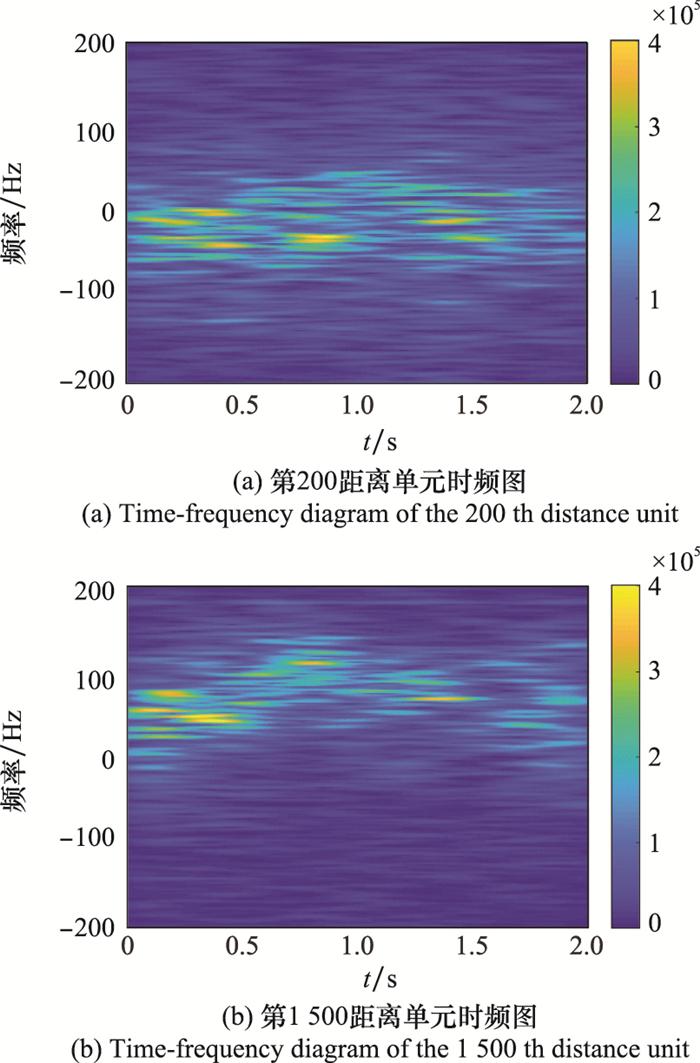
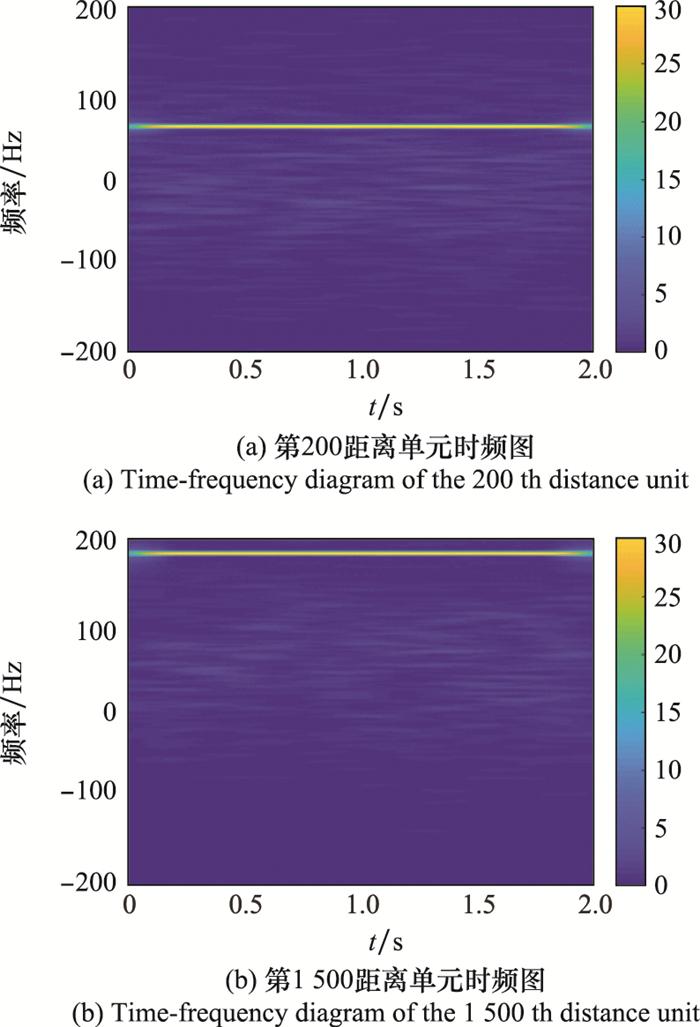
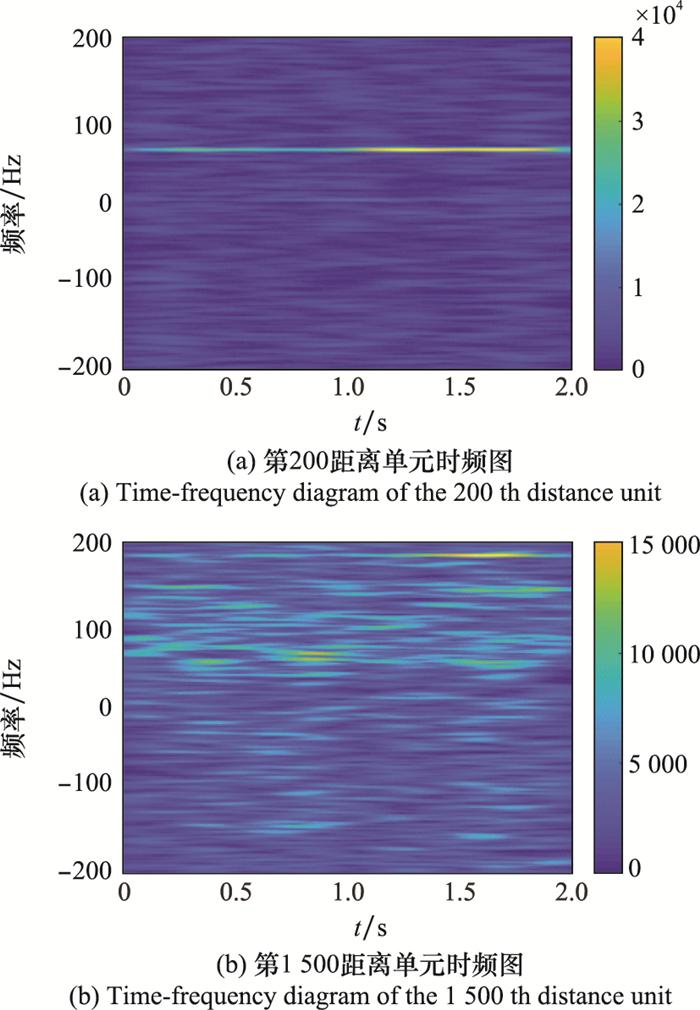
图 6为实测海杂波数据的第1 000个脉冲的时域图, 可以看出在时域中两目标均被海杂波淹没。图 7(a)和图 7(b)分别为第200和第1 500距离单元的时频图。从图 7中可以看出, 目标信号的中心频率被海杂波的频率覆盖, 目标信号被海杂波淹没, 传统基于频域滤波的算法不能将目标信号检测出。由于海况为高海况, 选取与其振荡特性相匹配的参数, 提高在原始回波信号与重构海杂波信号的差中失配的目标信号能量占比。图 8为经过TQWT算法的杂波抑制处理后第1 000个脉冲的时域图, 可以看出在时域中第200和第1 500距离单元的目标均被检测出来, 几乎没有虚警存在, 只是目标的幅度被抑制。图 9(a)和图 9(b)分别为经过TQWT算法的杂波抑制处理后, 第200和第1 500距离单元的时频图。可以清晰地观察到, 两目标的多普勒频率分别为62 Hz和186 Hz, 也就是分别以1 m/s和3 m/s的速度靠近雷达。因此, 在高海况条件下的低信杂比情况中, TQWT算法能有效抑制海杂波, 提高信杂比, 提高雷达检测弱目标的能力。
2.2.2 低海况条件下运动目标的检测
图10
图10
实测数据杂波+仿真目标信号时域分析(Q=2、r=3、J=5)
Fig.10
Time domain analysis of measured data clutter+ simulation target signal (Q=2、r=3、J=5)
图11
图11
实测数据杂波+仿真目标信号时频域分析(Q=2、r=3、J=5)
Fig.11
Time-frequency domain analysis of measured data clutter+simulation target signal (Q=2、r=3、J=5)
图12
图12
实测数据杂波+仿真目标信号TQWT抑制时域分析(Q=2、r=3、J=5)
Fig.12
Time domain analysis by TQWT suppression of measured data clutter+simulation target signal (Q=2、r=3、J=5)
图13
图13
实测数据杂波+仿真目标信号TQWT抑制时频域分析(Q=2、r=3、J=5)
Fig.13
Time-frequency domain analysis by TQWT suppression of measured data clutter+simulation target signal (Q=2、r=3、J=5)
图 10为实测海杂波数据的第1 000个脉冲的时域图, 可以看出在时域中两目标均被海杂波淹没。图 11(a)和图 11(b)分别为第200和第1 500距离单元的时频图, 目标的中心频率略高于海杂波的频率, 但是直接将目标提取出来并不容易。由于海况为低海况, 选取与其振荡特性相匹配的参数, 提高在原始回波信号与重构海杂波信号的差中失配的目标信号能量占比。图 12为经过TQWT算法的杂波抑制处理后第1 000个脉冲的时域图, 同样可以看出在时域中第200和第1 500距离单元的目标均被检测出来, 几乎没有虚警存在, 只是目标的幅度被抑制。经过TQWT算法处理, 图 13(a)和图 13(b)同样可以清晰地观察到, 两目标的多普勒频率分别为62 Hz和186 Hz, 也就是分别以1 m/s和3 m/s的速度靠近雷达。因此, 在低海况条件下本文提出的算法也可检测出具有不同多普勒频率的弱运动目标, 提高了雷达检测弱目标的能力。
2.2.3 算法对比分析
图14
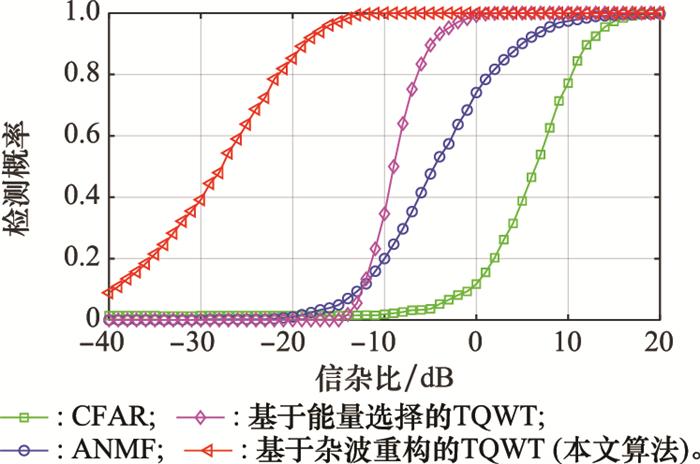
图 14为4种检测算法性能的对比图, 即强海杂波下信杂比与检测概率的关系。可知本文基于杂波重构TQWT算法的检测性能优于CFAR检测算法、ANMF处理算法和基于能量选择的TQWT算法。在信杂比为-10 dB的条件下, 基于杂波重构的TQWT算法的检测概率可达到1, 而此时基于能量选择的TQWT算法检测概率在0.3左右, CFAR检测和ANMF处理算法的检测概率接近于0。若要求0.9的检测概率, 本文基于杂波重构的TQWT算法所需的信杂比为-19 dB, 基于能量选择的TQWT算法所需信杂比为-5 dB, ANMF算法所需信杂比为5 dB, CFAR算法所需信杂比为12 dB。本文添加的目标为仿真目标, 与真实目标相比, 其与海杂波的相关性更弱, 在重构海杂波时, 能量损失更少。因此在处理真实目标时本文提出的改进的TQWT算法性能略有下降, 需要进一步验证。
3 结论
本文针对以海杂波为背景的弱目标检测中目标回波弱(即信杂比低)的问题, 改进了基于TQWT的海杂波抑制算法。通过选取与海杂波振荡特性相匹配的参数, 使经过TQWT后的小波子带呈现稀疏性, 经过BPD做稀疏优化处理和TQWT反变换进行海杂波重构, 最后将回波信号与海杂波重构信号的差作为检测样本, 通过本文提出的自适应阈值检测准则判断目标信号是否存在。该算法不依赖于具体的海杂波模型, 并且可以对接收的回波信号进行实时处理。对高海况和低海况下的实测海杂波数据进行处理的结果表明, 本文算法的检测性能优于CFAR检测算法、ANMF算法和基于能量选择的TQWT算法。由于本文算法时间复杂度稍大, 在硬件条件允许的情况下, 其性能将会优于传统算法。
参考文献
海杂波背景下雷达目标特征检测方法的现状与展望
[J].
Status and prospects of feature-based detection methods for floating targets on the sea surface
[J].
海杂波中的雷达目标检测技术综述
[J].DOI:10.3969/j.issn.1004-7859.2014.12.001 [本文引用: 1]
An overview on radar target detection in sea clutter
[J].DOI:10.3969/j.issn.1004-7859.2014.12.001 [本文引用: 1]
海洋环境中基于WVD的LFM信号检测方法
[J].
A new approach with Wigner-Ville distribution based on LFM signal detection in the ocean
[J].
Target detection in sea-clutter using stationary wavelet transform
[J].
改进型SVD-FRFT海杂波抑制方法
[J].
Improved SVD-FRFT sea clutter suppression method
[J].
时频域分解海面回波及慢速微弱目标检测
[J].
Detection of slow and weak target in time-frequency domain decomposition surface echo wave
[J].
一种基于能量选择的改进TQWT海杂波抑制算法
[J].
Improved TQWT sea clutter suppression algorithm based on energy selection
[J].
基于自适应可调Q因子小波变换的海杂波背景下的目标检测技术
[J].
Based on adaptive tunable Q-factor wavelet transform target detection technology under sea clutter background
[J].
Wavelet transform with tunable Q-factor
[J].
Sparse signal representations using the tunable Q-factor wavelet transform
[J].
Detection in sea clutter using sparse signal separation
[J].
Fast image recovery using variable splitting and constrained optimization
[J].
X波段雷达对海探测试验与数据获取
[J].
Sea-detecting X-band radar and data acquisition program
[J].
X波段雷达对海探测试验与数据获取年度进展
[J].
Annual progress of the sea-detecting X-band radar and data acquisition program
[J].