Systems Engineering and Electronics ›› 2025, Vol. 47 ›› Issue (9): 2925-2938.doi: 10.12305/j.issn.1001-506X.2025.09.14
• Systems Engineering • Previous Articles
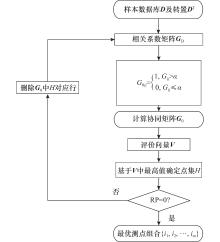
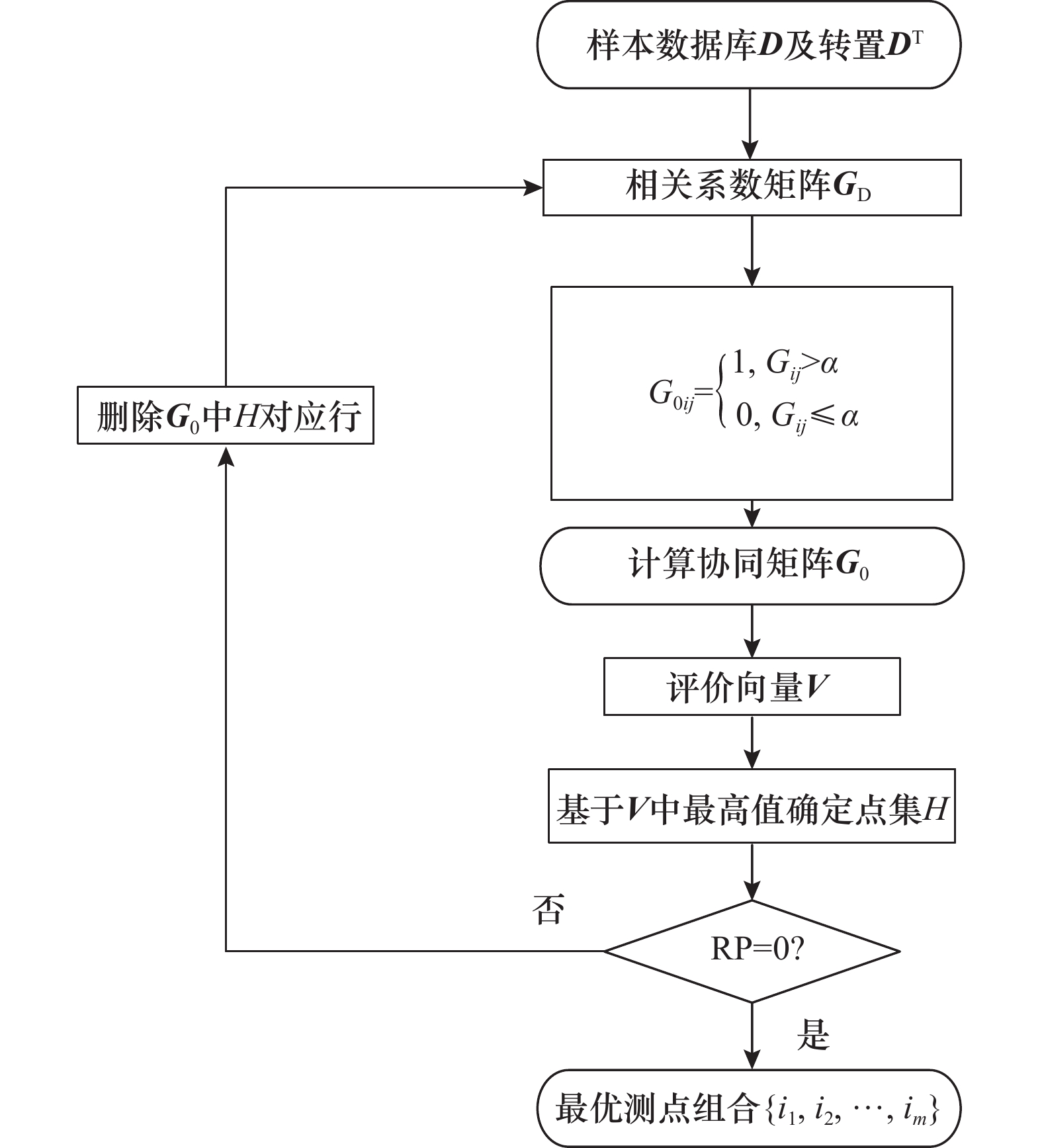
Correlation coefficient filtering method for optimizing system limited sensor layout
Qingyang YUAN1( ), Jiajie HAN1, Ke XUE2, Weijie SUN1, Bo ZHANG1,2,*(
), Jiajie HAN1, Ke XUE2, Weijie SUN1, Bo ZHANG1,2,*( )
)
- 1. School of Energy and Power,Dalian University of Technology,Dalian 116081,China
2. NingBo Institute of Dalian University of Technology,Ningbo 116038,China
-
Received:2024-06-20Online:2025-09-25Published:2025-09-16 -
Contact:Bo ZHANG E-mail:18842396497@163.com;Yuan_qingy@mail.dlut.edu.cn
CLC Number:
Cite this article
Qingyang YUAN, Jiajie HAN, Ke XUE, Weijie SUN, Bo ZHANG. Correlation coefficient filtering method for optimizing system limited sensor layout[J]. Systems Engineering and Electronics, 2025, 47(9): 2925-2938.
share this article
Table 1
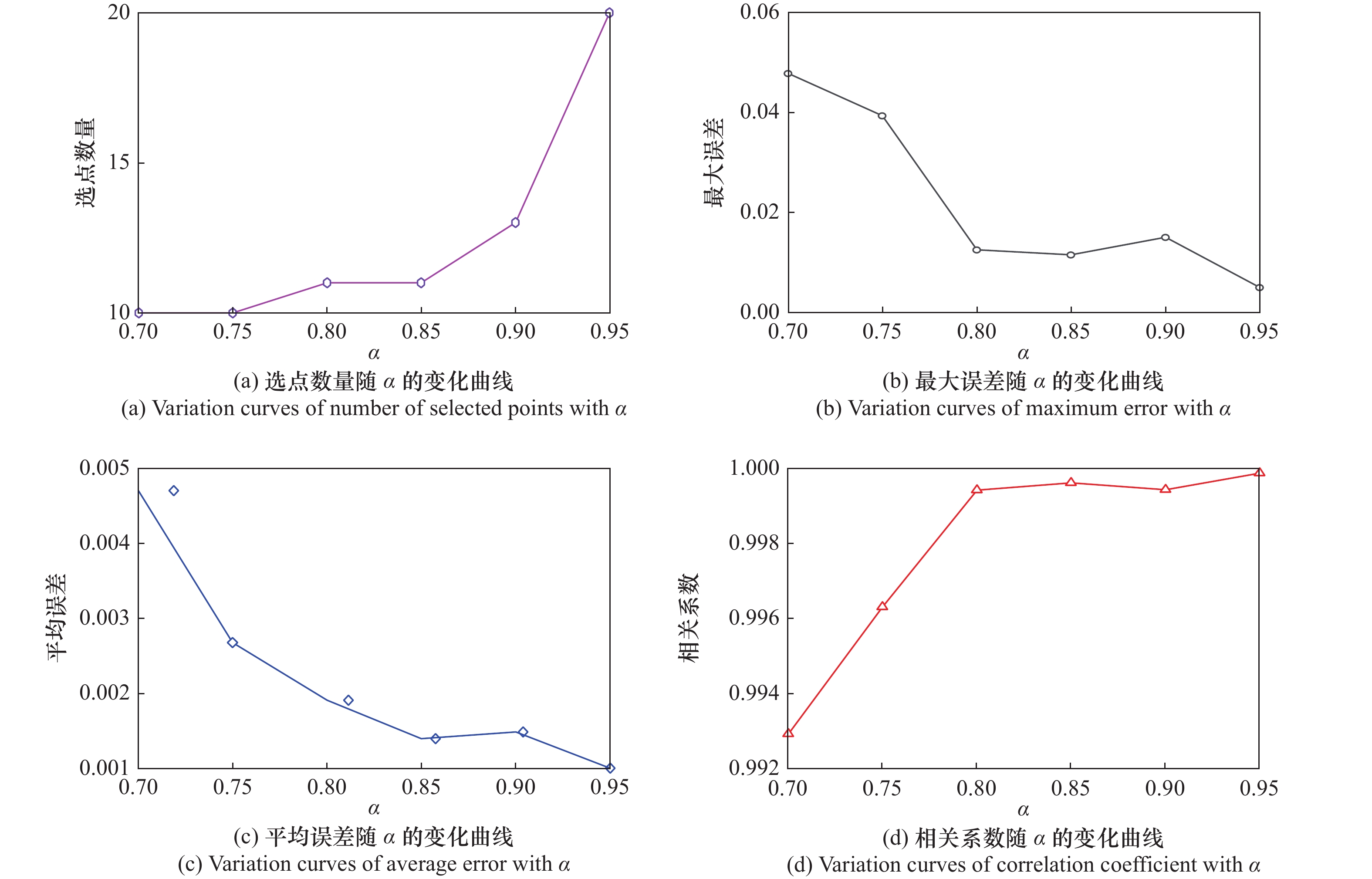
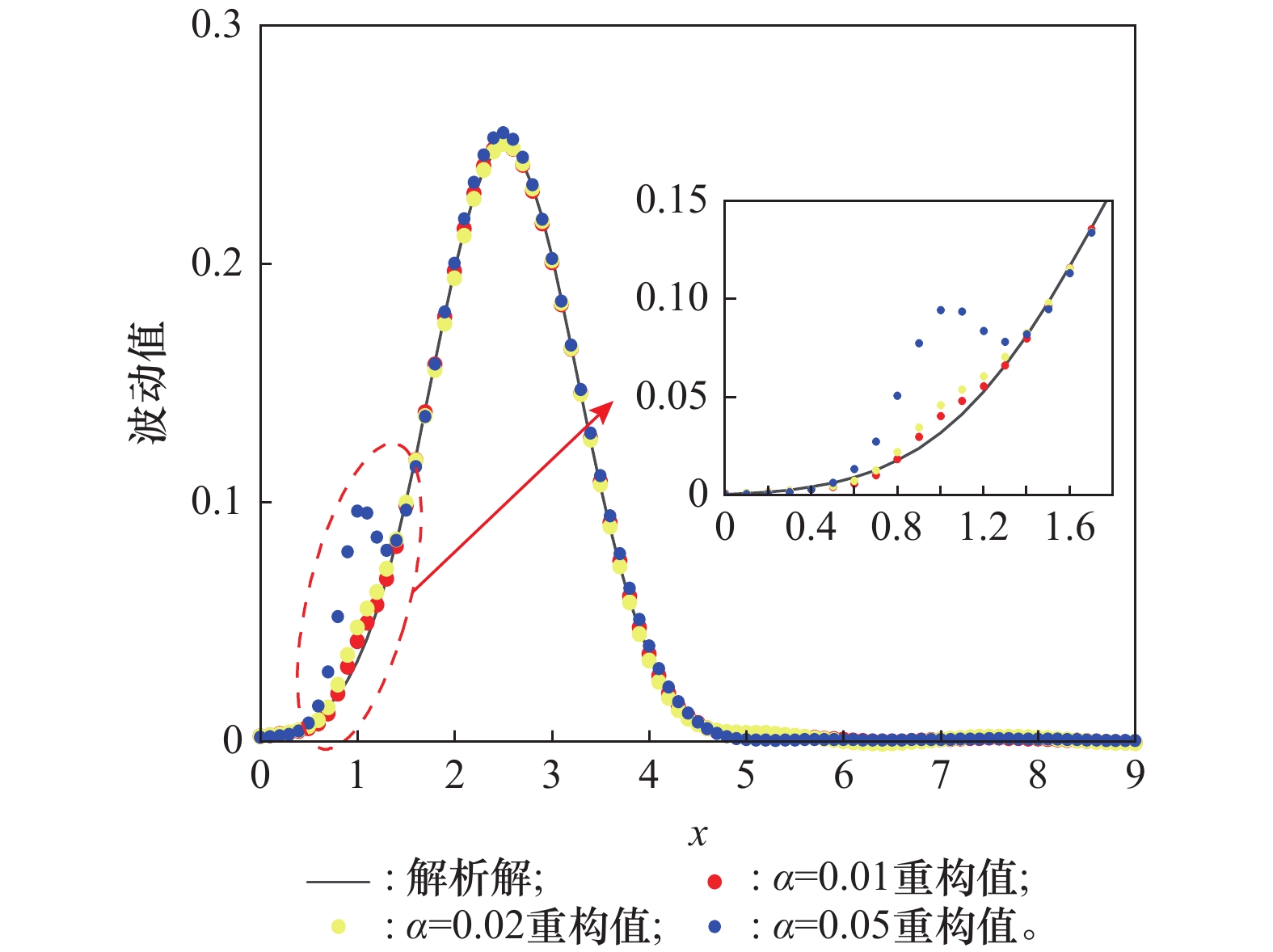
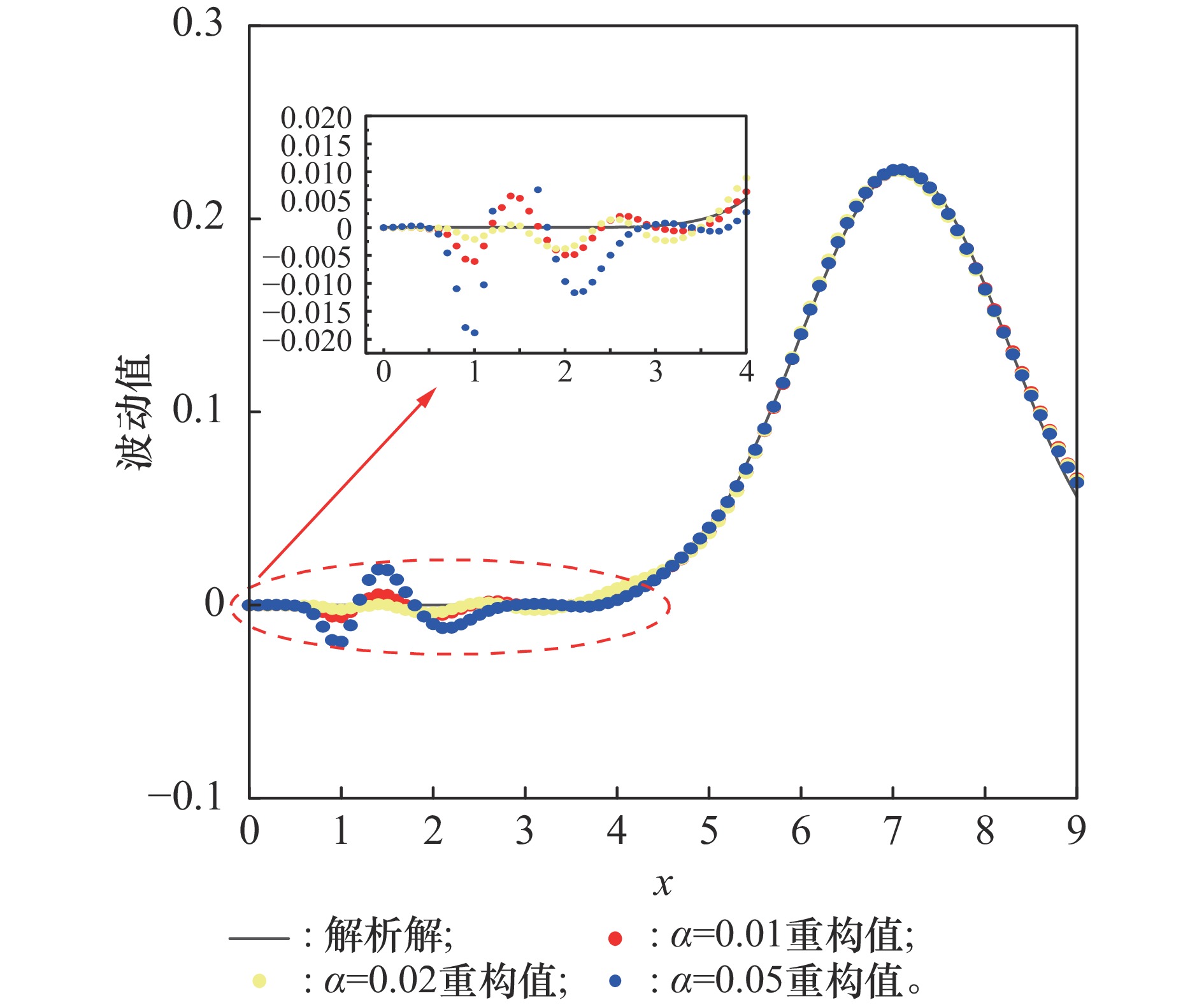
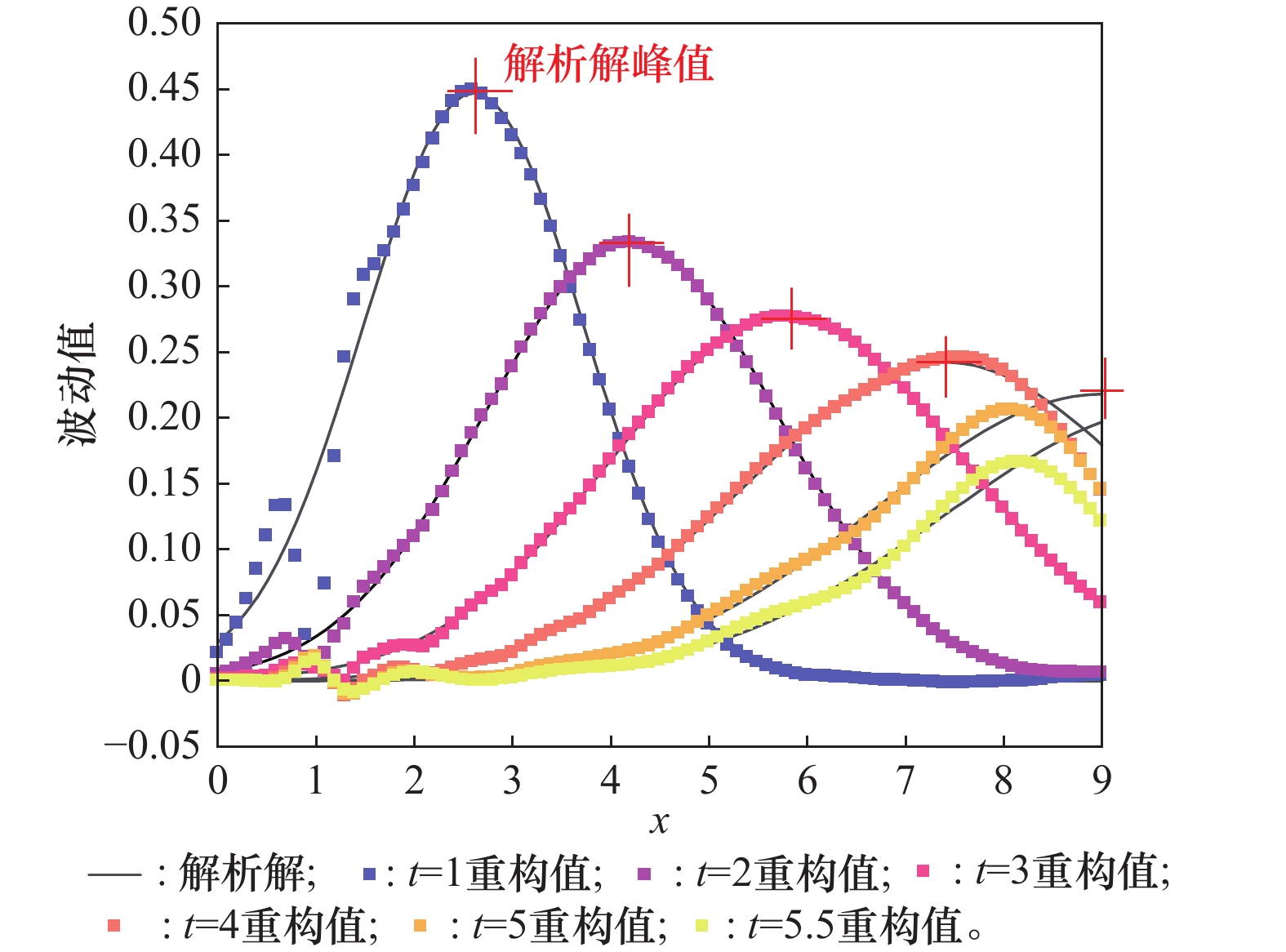
Influence of point selection on the reconstruction accuracy of one-dimensional Burgers’ equation with different α decay rates (U = 0.4,μ = 0.07,t = 3.8)"
| α趋势 | RP=1时α值 | 选点位置编号 | ME | AE | CCOE |
| 依次衰减0.01 | 0.82 | {84, 72, 58, 34, 48, 8, 27, 40, 17, 62, 3, 81, 20, 13} | {0.008, 752, 080} | {0.001, 144, 207} | {0.999, 758, 363} |
| 依次衰减0.02 | 0.69 | {84 58, 73, 48, 37, 8, 24, 16, 60, 3, 28, 37, 70, 16} | {0.014, 409, 187} | {0.001, 697, 398} | {0.999, 346, 946} |
| 依次衰减0.05 | 0.45 | {84, 60, 72, 46, 29, 6, 19, 33, 1, 44, 73} | {0.063, 146, 238} | {0.004, 131, 594} | {0.990, 416, 251} |
Table 2
Influence of point selection on the reconstruction accuracy of one-dimensional Burgers’ equation with different α decay rates (U = 1.3,μ = 0.13,t = 4.7)"
| α趋势 | RP=1时α值 | 选点位置编号 | ME | AE | CCOE |
| 依次衰减0.01 | 0.82 | {84, 72, 58, 34, 48, 8, 27, 40, 17, 62, 3, 81, 20, 13} | {0.009, 452, 472} | {0.002, 242, 488} | {0.999, 341, 769} |
| 依次衰减0.02 | 0.69 | {84, 58, 73, 48, 37, 8, 24, 16, 60, 3, 28, 37, 70, 16} | {0.008, 899, 572} | {0.002, 317, 576} | {0.999, 355, 279} |
| 依次衰减0.05 | 0.45 | {84, 60, 72, 46, 29, 6, 19, 33, 1, 44, 73} | {0.018, 826, 778} | {0.003, 432, 031} | {0.997, 668, 907} |
| 1 |
HASEGAWA K, FUKAMI K, MURATA T, et al. Machine-learning based reduced-order modeling for unsteady flows around bluff bodies of various shapes[J]. Theoretical and Computational Fluid Dynamics, 2020, 34 (4): 367- 383.
doi: 10.1007/s00162-020-00528-w |
| 2 |
RAHMAN M S, HAZRA S, CHOWDHURY I A. Advancing computational fluid dynamics through machine learning: a review of data-driven innovations and applications[J]. Journal of Fluid Mechanics and Mechanical Design, 2024, 6 (2): 42- 51.
doi: 10.46610/JFMMD.2024.v06i02.005 |
| 3 | GIOVANNI S, BOJANA R. Bayesian identi-fication of a projection-based reduced order model for computational fluid dynamics[J]. Computers & Fluids, 2020, 201, 104477. |
| 4 |
刘钊, 王沐晨, 李金玖, 等. 基于POD的尾流激励叶片气动力降阶模型[J]. 兵器装备工程学报, 2021, 42 (2): 82- 88.
doi: 10.11809/bqzbgcxb2021.02.015 |
|
LIU Z, WANG M C, LI J J, et al. Aerodyna-mic reduction model of wake excited blade based on POD[J]. Journal of Ordnance Equipment Engineering, 2021, 42 (2): 82- 88.
doi: 10.11809/bqzbgcxb2021.02.015 |
|
| 5 | MA H H, ZHENG X, WANG J P, et al. POD analysis and low-dimensional model based on POD-galerkin for two-dimensional Rayleigh-Benard convection[J]. Journal of Harbin Institute of Technology, 2018, 25 (1): 67- 78. |
| 6 | GU X J, XU C, LIU M, et al. Frequency-domain proper orthogonal decomposition for efficient reconstruction of unsteady flows[J]. Physics of Fluids, 2025, 37(2): 025161. |
| 7 |
KERSCHEN G, GOLINVAL J C, VAKAKIS A F, et al. The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: an overview[J]. Nonlinear Dynamics, 2005, 41, 147- 169.
doi: 10.1007/s11071-005-2803-2 |
| 8 | 闵光云, 姜乃斌. 基于POD方法的燃料棒模态特征及流致振动响应降阶模型研究[J]. 核动力工程, 2024, 45 (4): 142- 149. |
| MIN G Y, JIANG N B. Research on modal characteristics and order reduction model of fuel rod induced vibration response based on POD method[J]. Nuclear Power Engineering, 2024, 45 (4): 142- 149. | |
| 9 | CAO Y H, ZHU J, LUO Z D, et al. Reduced-order modeling of the upper tropical Pacific Ocean model using proper orthogonal decomposition[J]. Computers & Mathematics with Applications, 2006, 52 (8/9): 1373- 1386. |
| 10 | LI T Y, REN J H, WANG Q, et al. Research on rapid calculation method of ice cloud parameters based on POD-Kriging agent model[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2023, 40 (S1): 1- 12. |
| 11 |
EVERSON R, SIROVICH L. Karhunen-Loeve procedure for Gappy data[J]. Journal of the Optical Society of America a-Optics Image Science and Vision, 1995, 12 (8): 1657- 1664.
doi: 10.1364/JOSAA.12.001657 |
| 12 |
李天一, BUZZICOTTI M, BIFERALE L, 等. Gappy POD方法重构湍流数据的研究[J]. 力学学报, 2021, 53 (10): 2703- 2711.
doi: 10.6052/0459-1879-21-464 |
|
LI T Y, BUZZICOTTI M, BIFERALE L, et al. Reconstruction of turbulence data by Gappy POD method[J]. Chinese Journal of Mechanical Mechanics, 2021, 53 (10): 2703- 2711.
doi: 10.6052/0459-1879-21-464 |
|
| 13 | ZHANG W Q, LI H. A high-order proper orthogonal decomposition dimensionality reduction compact finite-difference method for diffusion problems[J]. Mathematical and Computational Applications, 2025, 30(4): 77. |
| 14 | SEKAR A P K, DOOREN M F V, KUHN M. Overcoming blade interference: a Gappy pod data reconstruction method for nacelle mounted lidar measurements[J] Journal of Physics: Conference Series, 2022, 2265: 022078. |
| 15 |
XING X Q, MY H, ZHANG B L, et al. Fusing sensor data with CFD results using Gappy pod[J]. Ocean Engineering, 2022, 246, 110549.
doi: 10.1016/j.oceaneng.2022.110549 |
| 16 | SEKAR A P K, DOOREN M F V, ROTT A, et al. Lower order description and reconstruction of sparse scanning lidar measurements of wind turbine inflow using proper orthogonal decomposition[J]. Remote Sensing, 2022, 14(11): 2681. |
| 17 |
TAEHYUN J, BONCHAN T, KIM H, et al. Effective sensor placement in a steam reformer using Gappy proper orthogonal decomposition[J]. Applied Thermal Engineering, 2019, 154, 419- 432.
doi: 10.1016/j.applthermaleng.2019.03.089 |
| 18 |
DANIELE V. Gappy data and reconstruction procedures for flow past a cylinder[J]. Journal of Fluid Mechanics, 2004, 519, 315- 336.
doi: 10.1017/S0022112004001338 |
| 19 |
ZHANG Z Q, XIU Y, GUANG L. POD-based constrained sensor placement and field reconstruction from noisy wind measurements: a perturbation study[J]. Mathematics, 2016, 4 (2): 26.
doi: 10.3390/math4020026 |
| 20 | WIILLCOX K. Unsteady flow sensing and estimation via the Gappy proper orthogonal decomposition[J]. Computers & Fluids, 2006, 35 (2): 208- 226. |
| 21 | YILDIRIM B C, CHRYSSOSTOMIDIS C, KAR-NIADAKIS G E. Efficient sensor placement for ocean measurements using low dimensional concepts[J]. Oceam Modelling, 2009, 27 (3/4): 160- 173. |
| 22 |
ZIMMERMANN R, WILLCOX K. An accelerated greedy missing point estimation procedure[J]. SIAM Journal on Scientific Computing, 2016, 38 (5): 2827- 2850.
doi: 10.1137/15M1042899 |
| 23 | 苑清扬, 薛珂, 张博, 等. Gappy POD算法重构储能电池组核心温度及与BP神经网络预测能力对比[J]. 工程科学学报, 2024, 46 (1): 166- 177. |
| YUAN Q Y, XUE K, ZHANG B, et al. Gappy POD algorithm for reconstructing the core temperature of energy-storage battery packs and its comparison with BP neural network prediction ability[J]. Chinese Journal of Engineering, 2024, 46 (1): 166- 177. | |
| 24 | YUAN Q Y, XUE K, ZHANG B, et al. Reconstruction of core temperrature of energy storage battery pack by Gappy pod algorithm and comparison with BP neural network[J]. Chinese Journal of Engineering Science, 2024, 46 (1): 166- 177. |
| 25 |
SIROVICH L. Turbulence and the dynamics of coherent structures. I. Coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45 (3): 561- 571.
doi: 10.1090/qam/910462 |
| 26 |
WANG X, LIU Y H, CAO Z Y, et al. Optimization of supply air parameters control based on gappy pod method for creating non-uniform temperature fields[J]. Buildings, 2023, 13 (7): 1690.
doi: 10.3390/buildings13071690 |
| 27 |
DEUS J, MARTIN E. Efficient cardiovas-cular parameters estimation for fluid structure simulations using Gappy proper orthogonal decomposition[J]. Annals of Biomedical Engineering, 2024, 52, 3037- 3052.
doi: 10.1007/s10439-024-03568-z |
| 28 | WANG Y L, LI C S, ZHU Z L, et al. Real-time stress field reconstruction method using online monitoring parameters for thick walled power plant components based on Gappy proper orthogonal decomposition[J]. International Journal of Pressure Vessels and Piping, 2024, 209: 105172. |
| 29 |
ROWEIS S, SAUL L. Nonlinear dimension-ality reduction by locally linear embedding[J]. Science, 2000, 290 (5500): 2323- 2326.
doi: 10.1126/science.290.5500.2323 |
| 30 | MIRSHAFIEI F, MCCLURE G, KAMLAN T, et al. Improved ice shedding modeling of iced cables: a comparison with experimental data[D]. Montreal: McGill University, 2010. |
| 31 | 屠珊, 孙弼, 毛靖儒. 用Richardson外推法分析流动传热层流问题的不确定度[J]. 西安交通大学学报, 1999, 33 (11): 49- 52. |
| TU S, SUN B, MAO J R. Richardson extrapolation method for analyzing the uncertainty of laminar flow problem in flow heat transfer[J]. Journal of Xi’an Jiaotong University, 1999, 33 (11): 49- 52. |
| No related articles found! |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||