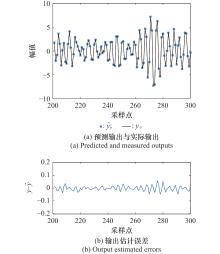
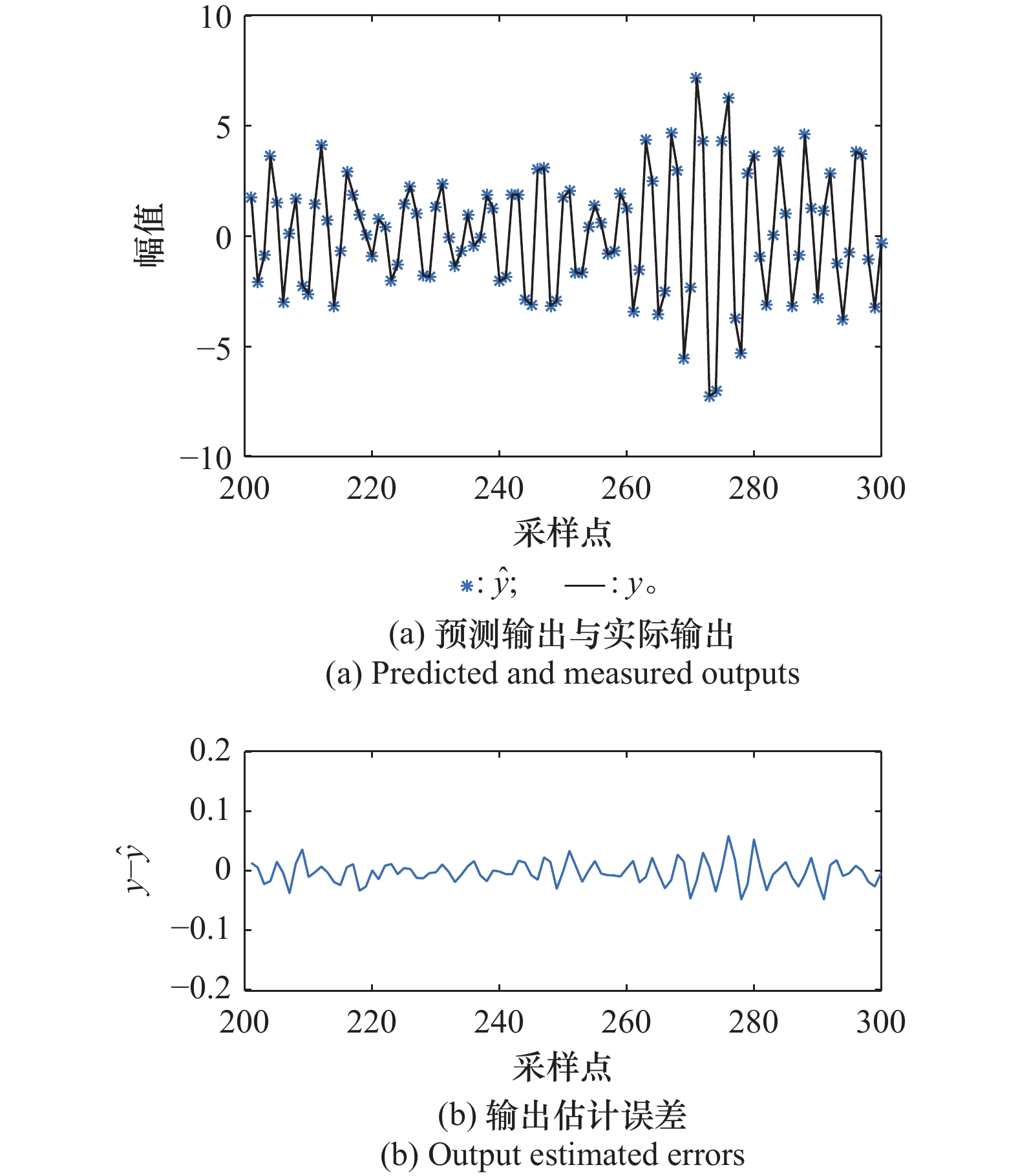
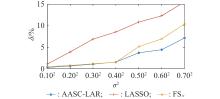
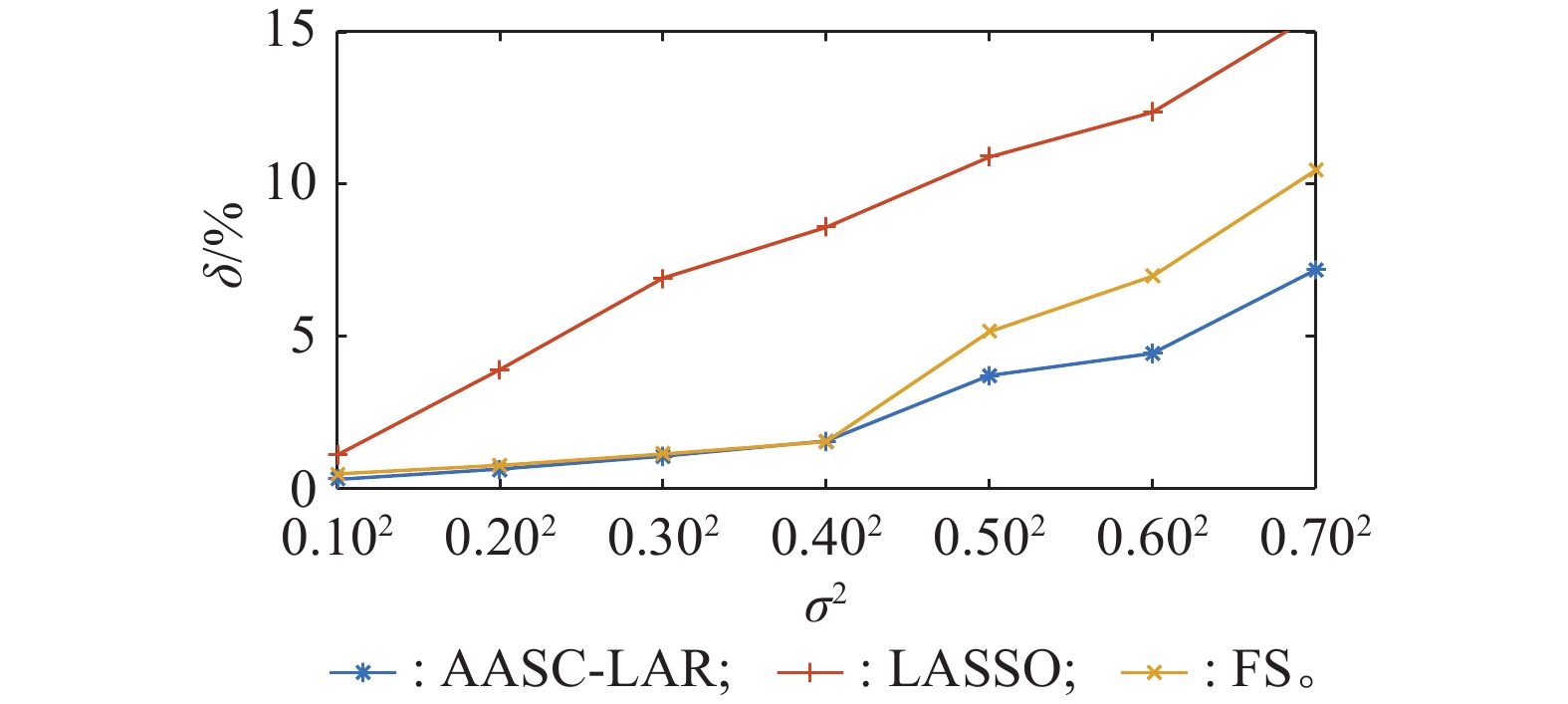
| 1 |
XIA Y Q, DAI L, SUN Z Q, et al. Design and implementation of data-driven predictive cloud control system[J]. Journal of Systems Engineering and Electronics, 2022, 33 (6): 1258- 1268.
|
| 2 |
ANASTASIA N, BRAATZ R D. Polynomial NARX-based nonlinear model predictive control of modular chemical systems[J]. Computers and Chemical Engineering, 2023, 117, 108272.
|
| 3 |
XU C Y, WANG Y, DUAN Y M. A general Boolean semantic modelling approach for complex and intelligent industrial systems in the framework of DES[J]. Journal of Systems Engineering and Electronics, 2024, 35 (5): 1219- 1230.
doi: 10.23919/JSEE.2024.000066
|
| 4 |
LIU Z W, HAN C Y, CHENG T J, et al. Servo turntable adaptive step size momentum projection identification algorithm based on ARX model[J]. Journal of the Franklin Institute, 2024, 361 (5): 106670.
doi: 10.1016/j.jfranklin.2024.106670
|
| 5 |
ZHANG J F, LIU L B, LIU Y M. A subspace based method for modelling building’s thermal dynamic in district heating system and parameter extrapolation verification[J]. Building Simulation, 2023, 16 (11): 2145- 2158.
doi: 10.1007/s12273-023-1002-8
|
| 6 |
NICO Z, TOBIAS B, JOSEF M, et al. Self-optimizing thermal error compensation models with adaptive inputs using group-lasso for ARX-models[J]. Journal of Manufacturing Systems, 2022, 64 (4): 615- 625.
|
| 7 |
PATTANAIK R, MOHANTY M, MOHAPATRA S, et al. Nonlinear dynamic system identification of ARX Model for speech signal identification[J]. Computer Systems Science and Engineering, 2023, 46 (1): 195- 208.
doi: 10.32604/csse.2023.029591
|
| 8 |
LIU X Y, LIU Y J, ZHU Q M, et al. Joint parameter and time-delay estimation for a class of Wiener models based on a new orthogonal least squares algorithm[J]. Nonlinear Dynamics, 2024, 112 (14): 12159- 12170.
doi: 10.1007/s11071-024-09651-3
|
| 9 |
刘艳君, 韩萍, 马君霞. 基于Householder变换的贪婪正交最小二乘辨识算法[J]. 控制与决策, 2022, 37 (9): 2281- 2286.
|
|
LIU Y J, HAN P, MA J X. Greedy orthogonal least squares identification algorithm based on Householder transformation[J]. Control and Decision, 2022, 37 (9): 2281- 2286.
|
| 10 |
WANG D Q, YAN Y R, LIU Y J, et al. Model recovery for Hammerstein systems using the hierarchical orthogonal matching pursuit method[J]. Journal of Computational and Applied Mathematics, 2019, 345, 135- 145.
doi: 10.1016/j.cam.2018.06.016
|
| 11 |
TIBSHIRANI R. Regression shrinkage and selection via the lasso: a retrospective[J]. Journal of the Royal Statistical Society Series B: Statistical Methodology, 2011, 73 (3): 273- 282.
doi: 10.1111/j.1467-9868.2011.00771.x
|
| 12 |
EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression[J]. Annals of Statistics, 2004, 32 (2): 407- 499.
|
| 13 |
刘艳君, 范晋翔, 陈晶. 基于改进最小角回归算法的Hammerstein模型辨识[J]. 控制理论与应用, 2024, 41 (9): 1644- 1652.
doi: 10.7641/CTA.2023.20719
|
|
LIU Y J, FAN J X, CHEN J. Identification for Hammerstein models based on a modified least angle regression algorithm[J]. Control Theory & Application, 2024, 41 (9): 1644- 1652.
doi: 10.7641/CTA.2023.20719
|
| 14 |
DING F, MENG D D, WANG Q. The model equivalence based parameter estimation methods for Box-Jenkins systems[J]. Journal of the Franklin Institute, 2015, 352 (12): 5473- 5485.
doi: 10.1016/j.jfranklin.2015.08.018
|
| 15 |
IOANNIS C, FADI D. Unbalance identification using the least angle regression technique[J]. Mechanical Systems and Signal Processing, 2015, 50 (5): 706- 717.
|
| 16 |
KIM W, KIM S, NA M H, et al. A modified least angle regression algorithm for interaction selection with heredity[J]. Statistical Analysis and Data Mining: The ASA Data Science Journal, 2022, 15 (5): 630- 647.
doi: 10.1002/sam.11577
|
| 17 |
ABEYSEKERA S K, KUANG Y C, OOI M P L, et al. Maximal associated regression: a nonlinear extension to least angle regression[J]. IEEE Access, 2021, 9, 159515- 159532.
doi: 10.1109/ACCESS.2021.3131740
|
| 18 |
方崇智, 萧德云. 过程辨识[M]. 北京: 清华大学出版社, 1988.
|
|
FANG C Z, XIAO D Y. Process identification[M]. Beijing: Tsinghua University Press, 1988.
|
| 19 |
刘宁, 柴天佑. PID控制器参数的优化整定方法[J]. 自动化学报, 2023, 49 (11): 2272- 2285.
|
|
LIU N, CHAI T Y. An optimal tuning method of PID controller parameters[J]. Acta Automatica Sinica, 2023, 49 (11): 2272- 2285.
|
| 20 |
SON D, CHOI H. Iterative feedback tuning of the proportional-integral-differential control of flow over a circular cylinder[J]. IEEE Trans. on Control Systems Technology, 2019, 27 (4): 1385- 1396.
doi: 10.1109/TCST.2018.2828381
|
| 21 |
VERMA B, PADHY P K. Indirect IMC-PID controller design[J]. IET Control Theory & Applications, 2019, 13 (2): 297- 305.
|
| 22 |
GARPINGER O, HAGGLUND T, ASTROM K J. Performance and robustness trade-offs in PID control[J]. Journal of Process Control, 2014, 24 (5): 568- 577.
doi: 10.1016/j.jprocont.2014.02.020
|
| 23 |
YIN M Z, MUELLER M A. Low-rank matrix regression via least-angle regression[J]. IEEE Control Letters, 2025, 9, 637- 642.
|
| 24 |
DONG L, XIAO F R. Carbon price prediction based on LsOALEO feature selection and time-delay least angle regression[J]. Journal of Cleaner Production, 2023, 416, 137853.
doi: 10.1016/j.jclepro.2023.137853
|
| 25 |
LI B, WANG Y Q, LI L S, et al. Research on apple origins classification optimization based on least-angle regression in instance selection[J]. Agriculture-Basel, 2023, 13 (10): 1868- 1882.
doi: 10.3390/agriculture13101868
|
| 26 |
CHEN Y L, ZHENG C Y, SUN G S, et al. Gold prospectivity modeling by combination of Laplacian eigenmaps and least angle regression[J]. Natural Resources Research, 2021, 31 (4): 2023- 2040.
|
| 27 |
YU A, WANG H F, LI J Q, et al. Reconstruction based on adaptive group least angle regression for fluorescence molecular tomography[J]. Biomedical Optics Express, 2023, 14 (5): 2225- 2239.
doi: 10.1364/BOE.486451
|
| 28 |
LU H X, ZHANG J, LI L Q, et al. Least angle regression combined with competitive adaptive re-weighted sampling for NIR spectral wavelength selection[J]. Spectroscopy and Spectral Analysis, 2021, 41 (6): 1782- 1788.
|
| 29 |
DAN S J. NIR spectroscopy fruit quality detection algorithm based on the least angle regression model[J]. International Journal of High Performance Systems Architecture, 2020, 9 (2): 128- 135.
|
| 30 |
HARKONEN M, SEI T, HIROSE Y. Holonomic extended least angle regression[J]. Information Geometry, 2020, 3 (2): 149- 181.
doi: 10.1007/s41884-020-00035-1
|